Abstract
Background
In countless number of clinical trials, measurements of outcomes rely on instrument questionnaire items which however often suffer measurement error problems which in turn affect statistical power of study designs. The Cronbach alpha or coefficient alpha, here denoted by Cα, can be used as a measure of internal consistency of parallel instrument items that are developed to measure a target unidimensional outcome construct. Scale score for the target construct is often represented by the sum of the item scores. However, power functions based on Cα have been lacking for various study designs.
Methods
We formulate a statistical model for parallel items to derive power functions as a function of Cα under several study designs. To this end, we assume fixed true score variance assumption as opposed to usual fixed total variance assumption. That assumption is critical and practically relevant to show that smaller measurement errors are inversely associated with higher inter-item correlations, and thus that greater Cα is associated with greater statistical power. We compare the derived theoretical statistical power with empirical power obtained through Monte Carlo simulations for the following comparisons: one-sample comparison of pre- and post-treatment mean differences, two-sample comparison of pre-post mean differences between groups, and two-sample comparison of mean differences between groups.
Results
It is shown that Cα is the same as a test-retest correlation of the scale scores of parallel items, which enables testing significance of Cα. Closed-form power functions and samples size determination formulas are derived in terms of Cα, for all of the aforementioned comparisons. Power functions are shown to be an increasing function of Cα, regardless of comparison of interest. The derived power functions are well validated by simulation studies that show that the magnitudes of theoretical power are virtually identical to those of the empirical power.
Conclusion
Regardless of research designs or settings, in order to increase statistical power, development and use of instruments with greater Cα, or equivalently with greater inter-item correlations, is crucial for trials that intend to use questionnaire items for measuring research outcomes.
Discussion
Further development of the power functions for binary or ordinal item scores and under more general item correlation strutures reflecting more real world situations would be a valuable future study.
Keywords: Cronbach alpha, Coefficient alpha, Test-retest correlation, Internal consistency, Reliability, Statistical power, Effect size
Background
Use of instrument questionnaire items is essential for measurement of outcome of interest in innumerable numbers of clinical trials. Many trials use well-established instruments; for example, major depressive disorders are often evaluated by scores on the Hamilton Rating Scale of Depression (HRSD) [1] in psychiatry trials. However, it is by far more often the case when instruments germane to a research outcome are not available. In such cases, of course, questionnaire items need to be developed to measure the outcome, and their psychometric properties should be evaluated for construct validity, internal consistency, and reliability among others [2, 3]. The internal consistency of instrument items quantifies how similarly in a interrelated fashion the items represent an outcome construct that the instrument is aiming to measure [4], whereas reliability is defined as the squared correlation between true score and observed score [3].
Cronbach alpha also known as coefficient alpha [5], hereafter denoted by Cα, has been very widely used to quantify the internal consistency and reliability of items in clinical research and beyond [6] although internal consistency and reliability are not exchangeable psychometric concepts in general. For this reason, some argue that Cα should not be used for quantifying either concept (e.g.,[7, 8]). One the other hand, for special cases where items under study are parallel such that items are designed as replicates to measure a unidimensional construct or attribute, Cα can quantify internal consistency and reliability as well [2] although in general Cα is not necessarily a measure of unidimensionality or homogeneity [4, 8]. In this paper, we consider parallel items; for example, items within a same factor could be considered parallel for a unidimensional construct. In this sense, items of HRSD are not parallel since it measures depression, a multidimensional construct with many factors.
The Cronbach alpha by mathematical definition is an adjusted proportion of total variance of the item scores explained by the sum of covariances between item scores, and thus ranges between 0 and 1 if all covariance elements are non-negative. Specifically, for an instrument with k items with a general covariance matrix Σ among the item scores, Cα is defined as
| 1 |
where trace(.) is the sum of the diagonal elements of a square matrix, 1 is a column vector with k unit elements, and 1T is the transpose of 1. This quantification is therefore based on the notion that relative magnitudes of covariances between item scores compared to those of corresponding variances serves as a measure of similarities of the items. Consequently, items with higher Cα are preferred to measure the target outcome. However, Cα is a lower bound for reliability, but is not equal to reliability unless the items are parallel or essentially τ-equivalent [3, 8]. The sum of the instrument items serves as a scale for the outcome, and is used for statistical inference including testing statistical hypotheses. At the design stage of clinical trials, information about magnitude of reliability or internal consistency of developed parallel items is crucial for power analysis and sample size determinations. Nonetheless, power functions based on Cα have been lacking for various study designs.
In this paper, to derive closed-from power functions, we formulate a statistical model for parallel items that relates the item scores to a measurement error problem. Under this model, Cα (1) is explicitly expressed in terms of an inter-item correlation. We examine relationship among Cα, a test-retest correlation and reliability of scale scores that enables testing significance of Cα through Fisher z-transformation. We explicitly express statistical power as a function of Cα for the following comparisons: one-sample comparison of pre- and post-treatment mean differences, two-sample comparison of pre-post mean differences between groups, and two-sample comparison of mean differences between groups. Simulation study results compare derived theoretical power with empirical power and discussion and conclusion follow.
Methods
Statistical model
We consider the following model for item score Yij to the j-th parallel item for the i-th subject:
| 2 |
The parameter μi represents the “true score” of the target (outcome) construct for the i-th subject. At the population level, its expectation and variance are assumed to be and , which we call the true score variance. The error term represents the deviate of the item score Yij from the true score μi, i.e., is the measurement error of Yij. The expectation and variance of for all subjects are assumed to be , i.e., unbiasedness assumption, that is, Ej(Yij) = μi and EiEj(Yij) = E(μi) = μ, where Ej denotes the expectation over j. It is also assumed that , which we call the measurement error variance. We further assume the following: μi and eij are mutually independent, i.e., μi ⊥ eij; and the elements of eij’s are independent for a given subject, i.e., conditional independence, that is, eij ⊥ eij′|μi for j ≠ j′. Note that this conditional independence does not imply marginal impendence between Yij and Yij′. In short, model (2) is a mixed-effects linear model for data with a two-level structure in a way that repeated item scores are nested within individuals.
Under those assumptions, we have , that is, the total variance of the item scores is the sum of the true score variance and the measurement error variance. Inter-item (score) covariance can be obtained as for j ≠ j′. Therefore, the diagonal elements of covariance matrix Σ under model (2) are identical and so are the off-diagonal elements. This compound symmetry covariance structure, also known as essential τ-equivalence, is the covariance matrix of parallel items each of which targets the underlying true score for a unidimensional construct. Furthermore, the compound symmetry covariance structure can be regarded as a covariance matrix of “standardized” item scores with unequal variances and covariances. Inter-item (score) correlation, denoted here by ρ, can accordingly be obtained as
| 3 |
Although item scores are correlated within subjects, they are independent between subjects. Note that this inter-item correlation is not necessarily equal to item-score reliability that quantifies a correlation between true and observed scores.
In this paper, we assume that the true score variance , instead of the total variance σ2, is fixed at the population level, and it does not depend on the item scores of the subjects. Stated differently, the total variance σ2 depends only on which depends on item scores and thus σ2 is assumed to be an increasing function of only measurement errors of the item scores. Let us call this assumption the fixed true score variance assumption, which is crucial and reasonable from the perspective of measurement error theory in general. This assumption is crucial because it makes the total variance as a function of only measurement error variance as mentioned above, and it is reasonable because at the population level true score variance should not be varying whereas magnitudes of measurement error variance depend on reliability of items. Consequently, the true score variance is not a function of inter-item correlation ρ, but the measurement error variance is a decreasing function of ρ since from equation (3) we have
| 4 |
It follows that as the item scores are closer or more similar to each other within subjects, the measurement errors will be smaller, which follows that the total variance is also a decreasing function of ρ since
| 5 |
We assume that the magnitudes of both and are known and thus that of σ2 for the purpose of derivation of power functions based on normal destructions instead of t-distributions, although replacement by t-distributions should be straightforward yet with little difference in results for sizable sample sizes.
Cronbach alpha, scale score and its variance
We assume that there are k items in an instrument, i.e., j =1, 2, …, k. The Cα (1) of k items under model (2) and aforementioned assumptions can be expressed as
| 6 |
It is due to the fact that under model (2) where I is a k-by-k identity matrix. Cα in equation (6) is seen to be an increasing function of both ρ and k as depicted in Fig. 1. Therefore, the number of items needs to be fixed for comparison of Cα of several candidate sets of items. It follows that for a fixed number of items, higher Cα is associated with smaller measurement error of items through higher inter-item correlation ρ. From equation (6), ρ can be expressed in terms of Cα as follows:
| 7 |
Fig. 1.
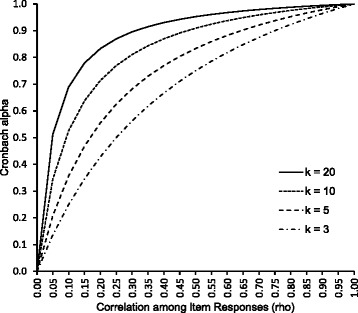
Relationship between Cronbach alpha (C α) and inter-item correlation (ρ) over varying number of items (k)
Of note, the corresponding correlation matrix is denoted by , an equi-correlation matrix.
The k correlated items are often summed up to a scale that is intended to measure the target construct. The scale score is denoted here by
which can be viewed as an observed summary score for the i-th subject. Suppressing the subscription i in Si, its mean and variance can be obtained as follows:
| 8 |
and
| 9 |
With respect to the mean (8), average scale score Si/k when used as observed score is an unbiased estimate of true score μi for the i-th subject. The reliability, denoted here by R, defined as the squared correlation between true score and observed score can be obtained as follows:
| 10 |
This equation supports Theorem 3.1 of Novick and Lewis [9] that R = Cα if and only if the items are parallel. Since statistical analysis results do not depend on whether Si/k or Si is used, we use the sum S in what follows.
With respect the total variance (9), if the total variance, instead of the true score variance, is assumed to be fixed, Var(S) is an increasing function of ρ, which conforms to an elementary statistical theory that variance of sum of correlated variables increases with increasing correlation. On the contrary, under the fixed true score variance assumption, it can be seen that Var(S) is a decreasing function of ρ since equation (9) can be re-expressed in terms of via equation (5) as follows:
| 11 |
The last equation is due to equation (7). It follows that Var(S) is also a decreasing function of Cα. In sum, increase of ρ decreases the magnitude of σ2 which in turn decreases the magnitude of Var(S); therefore such indirect decreasing effect of ρ on Var(S) is larger than direct increasing effect of ρ on Var(S) in equation (9).
Cronbach alpha and test-retest correlation
Reliability R of instruments is sometimes evaluated by test-retest correlation [3]. Based on model (2), the test and retest item scores can be specified as and , respectively with a common μi for both test and retest scores for each subject, i = 1, 2,…, N. The test-retest correlation can then be measured by the correlation, denoted by Corr(Stest, Sretest), between scale scores and representing the scale scores of test and retest, respectively. Under the aforementioned assumptions for model (2) it can be shown that
| 12 |
and from equation (10)
| 13 |
It follows that:
| 14 |
This equation shows that the test-rest correlation is the same as both Cα and R due to equations (6) and (10), which provides another interpretation of Cα. This property is especially useful when there is only one item available, in which case estimation of Cα or ρ is impossible by definition. However, the test and retest scores can be thought of as two correlated parallel item scores, and thus their correlation can serve as Cα of the single item. It is particularly fitting since ρ = Cα = R based on either equation (6), (7), or (14) when k = 1.
Taken together, the power of testing significance of Cα against any null value should be equivalent to that of testing significance of a correlation using a Fisher’s z-transformation as long as items are parallel, that is,
for a two-tailed significance level α, where Φ is the cumulative distribution function of a standardized normal distribution, and Φ−1 is its inverse function, i.e., Φ(Φ−1(x)) = Φ−1(Φ(x)) = x. We note that although it is necessary to be added for validation of unbiasedness of the test statistics under the null hypothesis, the probability under the other rejection area will be ignored for all test statistics considered herein. For general covariance structures for non-parallel items, however, many other tests for significance of reliability and Cα have been developed [10–17].
Pre-post comparison
We consider application of a paired t-test to the case of comparison of within-group means of scale scores between pre- and post-interventions. Based on model (2), the pre- and post-intervention item scores can be specified as and , respectively; the mean of the post-intervention item scores are shifted by δPP, an intervention effect. Consequently, we have
| 15 |
where and are the pre- and post-intervention scale scores, respectively. A moment estimate of δPP from (15) can be estimated as
| 16 |
where and N is the total number of subject. Its variance can be obtained as
| 17 |
It is because from equations (12) and (13) we have
The following test statistic can then be used for testing H0: δ = 0
| 18 |
Now, the statistical power φPP of TPP for detecting non-zero δPP can be expressed as follows:
| 19 |
This statistical power is an increasing function of ρ for a fixed σμ, which we assume. It follows that the power is also an increasing function of Cα as seen next. When δPP is standardized by σμ and ρ is replaced by equation (7), equation (19) can further be expressed in terms of and Cα as follows:
| 20 |
This power function is seen to be independent of k, the number of items. Stated differently, the power will be the same between two instruments with different numbers of items as long as their Cα’s are the same even if the correlation of items will be smaller for the instrument with fewer items.
When sample size determination is needed for a study using an instrument of any number of items with a known Cα for a desired statistical power φ, typically 80 %, it can be determined from equation as follows:
| 21 |
where
| 22 |
The sample size (21) is seen to be a decreasing function of increasing Cα and Δ. In a possibly rare case in which determination of number of items with known correlations among them is needed for development of an instrument, it has to be determined from equation (19), instead of equation (20), as follow:
| 23 |
Comparison of within-group effects between groups
In clinical trials, it is often of interest to compare within-group changes between groups. For instance, a clinical trial can be designed to compare of pre-post effect of an experimental treatment between treatment and control groups, that is, an interaction effect between group and time point. Based on model (2), the pre- and post-intervention item scores can be specified as and for the control group and for the treatment group. The primary interest will be testing Ho: δBW = δ1 – δ0 = 0, i.e., whether or not the difference in pre-post differences between groups will be the same. Consequently, we have
| 24 |
where and can be similarly defined. A moment estimate of δBW from (24) can be obtained as
| 25 |
where N is the number of subjects per group, , and, can similarly be defined. The variance of is
| 26 |
Therefore, the following test statistic can be used for testing the null hypothesis Ho: δBW = 0,
| 27 |
The statistical power φBW of TBW for detecting non-zero δBW can thus be expressed as follows:
| 28 |
Again, this statistical power is an increasing of ρ and of Cα as well as seen next. When δBW is standardized by σμ and ρ is replaced by equation (7), equation (28) can further be expressed in terms of and Cα as follows:
| 29 |
Again, this power function is seen to be independent of k, the number of items.
Sample size for a desired statistical power φ can be determined from (27) as follows:
| 30 |
Again, this sample size (30) is seen to be a decreasing function of increasing Cα and Δ. When number of items is needed for development of an instrument, it can be determined from equation (28) as follow:
| 31 |
Two-sample between-group comparison
Comparison of means between groups using an instrument is widely tested in clinical trials. Based on model (2), the intervention item scores from control and treatment groups can be specified as and , respectively. The primary interest will be testing Ho: δTS = 0, i.e., whether or not the means are the same between the two groups. Under this formulation, we have
| 32 |
where and represents scale scores under treatment and control groups, respectively. A moment estimate of δTS can be obtained from (32) as
| 33 |
where , and N is the number of participants per group. The variance of can be obtained as
| 34 |
The corresponding test statistic TTS can be built as
| 35 |
And the power function φTS of TTS can be expressed as
| 36 |
It should be noted that this statistical power (36) is also an increasing function of ρ in contrast to a situation when a fixed total variance assumption is more reasonable in which both and are a function of ρ but σ2 is not. For example, observations without measurement errors from clusters are often assumed to be correlated and power of between-group tests using such correlated observations is a decreasing function of ρ [18]. Again, when δTS is standardized by σμ and ρ is replaced by equation (7), equation (33) can further be expressed in terms can further be expressed in terms of and Cα as follows:
| 37 |
Again, this power function is seen to be independent of k, the number of items.
Sample size for a desired statistical power φ can be determined from (37) as follows:
| 38 |
Again, the sample size (38) is seen to be a decreasing function of increasing Cα and Δ. When number of items is needed for development of an instrument, it can be determined from equation (36) as follow:
| 39 |
Results
To validate equation (14) and the power functions (20), (29), and (37), we conduct simulation study for each test. For the simulation, the random item scores are generated based on model (2) assuming both μi and eij are normally distributed although this assumption is not required in general. Under this normal assumption, however, it can be shown that all the moment estimates herein are the maximum likelihood estimates [19]. We then compute scale scores by summing up the item scores for each individual.
We fix a two-tailed significance level of α = 0.05 and = 1 without loss generality for all simulations, and determine and σ2 through ρ determined by given k and Cα. We randomly generate 1000 data sets for each combination of design parameters that include effect size Δ, number of items k, and sample size N. We then compute empirical power by counting data sets from which two-tailed p-values are smaller than 0.05; that is, where ps represents a two-sided p-value from the s-th simulated data set. For the testing, we applied corresponding t-tests assuming the variances of the moment estimates are unknown, which is practically reasonable. We used SAS v9.3 for the simulations.
Test-retest correlation
The results are presented in Table 1 that shows the empirically estimated test-retest correlations (i.e., average of 1000 estimated Pearson correlations for each set of design parameter specifications) are approximately the same as the pre-assigned Cα, regardless of sample size N, which is as small as 30, and number of items k. Therefore, equality between Cα and test-retest correlation (14) is well validated.
Table 1.
Empirical simulation-based estimates of test-retest correlation Corr(S test, S retest) in equation (14)
| Corr(S test, S retest) | ||||
|---|---|---|---|---|
| Total N = 30 | Total N = 50 | |||
| C α | k = 5 | k = 10 | k = 5 | k = 10 |
| 0.1 | 0.10 | 0.10 | 0.10 | 0.10 |
| 0.2 | 0.20 | 0.20 | 0.20 | 0.20 |
| 0.3 | 0.30 | 0.29 | 0.30 | 0.30 |
| 0.4 | 0.39 | 0.39 | 0.40 | 0.39 |
| 0.5 | 0.49 | 0.50 | 0.49 | 0.50 |
| 0.6 | 0.59 | 0.59 | 0.60 | 0.60 |
| 0.7 | 0.69 | 0.69 | 0.70 | 0.70 |
| 0.8 | 0.79 | 0.80 | 0.80 | 0.79 |
| 0.9 | 0.90 | 0.90 | 0.90 | 0.90 |
Note: Total N: total number of subjects; C α: Cronbach alpha; k: number of items
Pre-post intervention comparison
Table 2 shows that the theoretical power φPP (20) is very close to the empirical power obtained through the simulations. The results validate that the power φPP increases with increasing Cα (or equivalently increasing correlation for the same k) in the “pre-post” test settings, regardless of sample size N and number of items k. Furthermore, it shows that the statistical power does not depend on k for a given Cα even if correlation ρ does.
Table 2.
Statistical power of the pre-post test T PP (18): σ μ = 1
| k = 5 | k = 10 | |||||
|---|---|---|---|---|---|---|
| Total N | Δ PP | C α | φ PP | φ PP | ||
| 30 | 0.4 | 0.5 | 0.341 | 0.337 | 0.341 | 0.310 |
| 0.6 | 0.475 | 0.459 | 0.475 | 0.458 | ||
| 0.7 | 0.658 | 0.626 | 0.658 | 0.649 | ||
| 0.8 | 0.873 | 0.849 | 0.873 | 0.830 | ||
| 0.9 | 0.996 | 0.997 | 0.996 | 0.995 | ||
| 50 | 0.3 | 0.5 | 0.323 | 0.309 | 0.323 | 0.296 |
| 0.6 | 0.451 | 0.424 | 0.451 | 0.433 | ||
| 0.7 | 0.630 | 0.633 | 0.630 | 0.614 | ||
| 0.8 | 0.851 | 0.849 | 0.851 | 0.844 | ||
| 0.9 | 0.994 | 0.995 | 0.994 | 0.992 | ||
Note: Total N: total number of subjects; k: number of items; ; C α: Cronbach alpha; φ PP: theoretical power (20); : simulation-based empirical power
Between-group whithin-group comparison
Table 3 shows that the theoretical power φBW (29) is very close to the empirical power obtained through the simulations. Therefore, the results validate that the statistical power φBW increases with increasing Cα for testing hypotheses concerning between-group effects on within-group changes regardless of N, sample size per group, and k. Again, it shows that the statistical power does not depend on k for a given Cα even if correlation ρ does.
Table 3.
Statistical power of the between-group within-group test T BW (25): σ μ = 1
| k = 5 | k = 10 | |||||
|---|---|---|---|---|---|---|
| N per group | Δ BW | C α | φ BW | φ BW | ||
| 30 | 0.4 | 0.5 | 0.194 | 0.179 | 0.183 | 0.194 |
| 0.6 | 0.268 | 0.264 | 0.254 | 0.268 | ||
| 0.7 | 0.387 | 0.375 | 0.359 | 0.387 | ||
| 0.8 | 0.591 | 0.618 | 0.594 | 0.591 | ||
| 0.9 | 0.908 | 0.884 | 0.901 | 0.908 | ||
| 50 | 0.3 | 0.5 | 0.164 | 0.184 | 0.214 | 0.184 |
| 0.6 | 0.242 | 0.254 | 0.261 | 0.254 | ||
| 0.7 | 0.387 | 0.367 | 0.365 | 0.367 | ||
| 0.8 | 0.511 | 0.564 | 0.591 | 0.564 | ||
| 0.9 | 0.893 | 0.889 | 0.893 | 0.889 | ||
Note: N per group: number of subjects per group; k: number of items; ; C α: Cronbach alpha; φ BW: theoretical power (27); : simulation-based empirical power
Two-sample between-group comparison
Table 4 shows again that the theoretical power φTS (37) is very close to the empirical power obtained through the simulations. The results validate that the statistical power increases with increasing Cronbach α even for two-sample testing in cross-sectional settings that does not involve within-group effects. it shows that the statistical power does not depend on k for a given Cα even if correlation ρ does. Again, it shows that the statistical power does not depend on k for a given Cα even if correlation ρ does.
Table 4.
Statistical power of the between-group within-group test T TS (32): σ μ = 1
| k = 5 | k = 10 | |||||
|---|---|---|---|---|---|---|
| N per group | Δ TS | C α | φ TS | φ TS | ||
| 50 | 0.7 | 0.5 | 0.697 | 0.676 | 0.697 | 0.697 |
| 0.6 | 0.774 | 0.758 | 0.774 | 0.760 | ||
| 0.7 | 0.834 | 0.812 | 0.834 | 0.813 | ||
| 0.8 | 0.879 | 0.872 | 0.879 | 0.882 | ||
| 0.9 | 0.913 | 0.901 | 0.913 | 0.895 | ||
| 100 | 0.5 | 0.5 | 0.705 | 0.682 | 0.705 | 0.679 |
| 0.6 | 0.782 | 0.791 | 0.782 | 0.769 | ||
| 0.7 | 0.841 | 0.820 | 0.841 | 0.832 | ||
| 0.8 | 0.885 | 0.879 | 0.885 | 0.908 | ||
| 0.9 | 0.918 | 0.929 | 0.918 | 0.912 | ||
Note: N per group: number of subjects per group; k: number of items; ; C α: Cronbach alpha; φ TS: theoretical power (34); : simulation-based empirical power
Discussion
We demonstrate by deriving explicit power functions that higher internal consistency or reliability of unidimensional parallel instrument items measured by Cronbach alpha Cα results in greater statistical power of several tests regardless of whether comparisons are made within or between groups. In addition, the test-retest reliability correlation of such items is shown to be the same as Cronbach alpha Cα. Due to this property, testing significance of Cα can be equivalent to testing that of a correlation through the Fisher z-transformation. Furthermore, all of the power functions derived herein can even be applied to trials using single item instrument with measurement error since the power function depends only on Cα which can be estimated via test-retest correlations for single item instruments as mentioned earlier. The demonstrations are made theoretically, and validations are made through simulation studies that show that the derived test statistics and their corresponding power functions are very close to each other. Therefore, the sample size determination formulas (21), (30), and (38) are valid and so are the determinations of number of items (22), (31), and (39) in different settings.
In fact, for longitudinal studies aiming to compare within-group effects using such as TPP (18) and TBW (27), the fixed true score variance assumption is not critical since the true score μi’s in model (2) are cancelled by taking differences of Y between pre and post-interventions and thus makes the variance of the pre-post differences depend only on measurement error variance . For example, the variance equations (17) and (26) can be expressed in term of only , a decreasing function of ρ, through equation (4) as follows: and . In other words, both the power functions φPP (20) and φBW (29) are increasing function of Cα or ρ regardless of whether total variance or true score variance is assumed fixed.
In contrast, however, for cross-sectional studies aiming to compare between-group effects using TTS (35), the fixed true score variance assumption is critical since the variance equation (34) cannot be expressed only in term of only , and furthermore it can be shown that under a fixed total variance assumption (34) is an increasing function of ρ (see equation (10)) and so is the power function. In sum, the fixed true score variance assumption enables all of the power functions to be an increasing function of Cα or ρ in a unified fashion. For example, Leon et al. [20] used a real data set of HRSD ratings to empirically demonstrate that the statistical power of a two-sample between-group test is increasing with increased Cα, although they increased Cα by increasing number of items k, not necessarily by increasing ρ for a fixed number of items.
In most cases, item scores are designed to be binary or ordinal scores on a likert scale. Therefore, the applicability of the derived power functions and sample size formulas to such cases could be in question since the scores are not normally distributed. Furthermore, it is not easy to build a model like (2) for non-normal scores particularly because measurement error variances depend on the true construct value. For example, variance of a binary score is a function of its mean. Perhaps, construction of marginal models in the sense of generalized estimating equations [21] can be considered for derivation of power functions assumption even if this approach is beyond the scope of the present study. After all, we believe that our study results should be able to be applied to non-normal scores by virtue of the central limit theorem. Another prominent limitation of our study is the very strong assumption of essentially τ-equivalent parallel items which may not be realistic at all [8], albeit conceivable for a unidimensional construct. Therefore, further development of power functions under relaxed conditions reflecting more real world situations should be a valuable future study.
Conclusion
Instruments with greater Cronbach alpha should be used for any type of research since they have smaller measurement error and thus have greater statistical power for any research settings, cross-sectional or longitudinal. However, when items are parallel targeting a unidimensional construct, Cronbach alpha of an instrument should be enhanced by developing a set of highly correlated items but not by unduly increasing the number of items with inadequate inter-item correlations.
Acknowledgements
We are grateful to the late Dr. Andrew C. Leon for initial discussion of the problems under study.
Funding
This work was in part supported by the NIH grants P30MH068638, UL1 TR001073, and the Albert Einstein College of Medicine funds.
Abbreviations
- HRSD
Hamilton Rating Scale of Depression
Footnotes
Competing interests
The authors declare that they have no competing interest.
Authors’ contributions
MH developed the methods, conducted simulation studies, and prepared a draft. NK and MSF provided critical reviews, corrections and revisions. All authors read and approved the final version of the manuscript.
Authors’ information
MH is a PhD in Statistics and Professor of Epidemiology and Population Health with collaborative backgrounds in Psychiatry. NK holds dual PhD’s in Statistics and is Assistant Research Professor of Radiology. MSF is a PhD in Psychology and Associate Professor of Nutrition.
Availability of data and materials
Not applicable.
Contributor Information
Moonseong Heo, Phone: 718-920-6274, Email: moonseong.heo@einstein.yu.edu.
Namhee Kim, Email: namhee.kim@einstein.yu.edu.
Myles S. Faith, mfaith@email.unc.edu
References
- 1.Hamilton M. A rating scale for depression. J Neurol Neurosurg Psychiatry. 1960;23:56–62. doi: 10.1136/jnnp.23.1.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nunnally JC, Bernstein IH. Psychometric Theory. 3. New York: McGraw-Hill; 1994. [Google Scholar]
- 3.Lord FM, Novick MR. Statistical Theories of Mental Test Scores. Reading, MA: Addison-Wesley; 1968. [Google Scholar]
- 4.Schmitt N. Uses and abuses of coefficient alpha. Psychol Assess. 1996;8(4):350–353. doi: 10.1037/1040-3590.8.4.350. [DOI] [Google Scholar]
- 5.Cronbach L. Coefficeint alpha and the internal struture of tests. Psychometrika. 1951;16:297–334. doi: 10.1007/BF02310555. [DOI] [Google Scholar]
- 6.Bland JM, Altman DG. Cronbach’s alpha. Br Med J. 1997;314(7080):572–2. [DOI] [PMC free article] [PubMed]
- 7.Cortina JM. What is coefficient alpha - An exmination of theory and applications. J Appl Psychol. 1993;78(1):98–104. doi: 10.1037/0021-9010.78.1.98. [DOI] [Google Scholar]
- 8.Sijtsma K. On the Use, the Misuse, and the Very Limited Usefulness of Cronbach’s Alpha. Psychometrika. 2009;74(1):107–120. doi: 10.1007/s11336-008-9101-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Novick MR, Lewis C. Coefficient alpha and the reliability of composite measurements. Psychometrika. 1967;32(1):1–13. doi: 10.1007/BF02289400. [DOI] [PubMed] [Google Scholar]
- 10.Charter RA. Statistical approaches to achieving sufficiently high test score reliabilities for research purposes. J Gen Psychol. 2008;135(3):241–251. doi: 10.3200/GENP.135.3.241-251. [DOI] [PubMed] [Google Scholar]
- 11.Feldt LS, Charter RA. Estimating the reliability of a test split into two parts of equal or unequal length. Psychol Methods. 2003;8(1):102–109. doi: 10.1037/1082-989X.8.1.102. [DOI] [PubMed] [Google Scholar]
- 12.Feldt LS, Ankenmann RD. Determining sample size for a test of the equality of alpha coefficients when the number of part-tests is small. Psychol Methods. 1999;4(4):366–377. doi: 10.1037/1082-989X.4.4.366. [DOI] [Google Scholar]
- 13.Feldt LS, Ankenmann RD. Appropriate sample size for comparing alpha reliabilities. Appl Psychol Meas. 1998;22(2):170–178. doi: 10.1177/01466216980222006. [DOI] [Google Scholar]
- 14.Padilla MA, Divers J, Newton M. Coefficient Alpha Bootstrap Confidence Interval Under Nonnormality. Appl Psychol Meas. 2012;36(5):331–348. doi: 10.1177/0146621612445470. [DOI] [Google Scholar]
- 15.Bonett DG, Wright TA. Cronbach’s alpha reliability: Interval estimation, hypothesis testing, and sample size planning. J Organ Behav. 2015;36(1):3–15. doi: 10.1002/job.1960. [DOI] [Google Scholar]
- 16.Bonett DG. Sample size requirements for testing and estimating coefficient alpha. J Educ Behav Stat. 2002;27(4):335–340. doi: 10.3102/10769986027004335. [DOI] [Google Scholar]
- 17.Bonett DG. Sample size requirements for comparing two alpha coefficients. Appl Psychol Meas. 2003;27(1):72–74. doi: 10.1177/0146621602239477. [DOI] [Google Scholar]
- 18.Donner A, Birkett N, Buck C. Randomization by cluster. Sample size requirements and analysis. Am J Epidemiol. 1981;114(6):906–914. doi: 10.1093/oxfordjournals.aje.a113261. [DOI] [PubMed] [Google Scholar]
- 19.Goldstein H. Multilevel Statistical Models. 2. New York: Wiley & Sons; 1996. [Google Scholar]
- 20.Leon AC, Marzuk PM, Portera L. More reliable outcome measures can reduce sample size requirements. Arch Gen Psychiatry. 1995;52(10):867–871. doi: 10.1001/archpsyc.1995.03950220077014. [DOI] [PubMed] [Google Scholar]
- 21.Zeger SL, Liang KY, Albert PS. Models for longitudinal data - A generalized estimating equation approach. Biometrics. 1988;44(4):1049–1060. doi: 10.2307/2531734. [DOI] [PubMed] [Google Scholar]


