MPnRAGE: A technique to simultaneously acquire hundreds of differently contrasted MPRAGE images with applications to quantitative T₁ mapping

Abstract

Purpose

To introduce a new technique called MPnRAGE, which produces hundreds of images with different T₁ contrasts and a B1 corrected T₁ map.

Theory and Methods

An interleaved 3D radial k-space trajectory with a sliding window reconstruction is used in conjunction with magnetization preparation pulses. This work modifies the SNAPSHOT-FLASH T₁ fitting equations for radial imaging with view-sharing and develops a new rapid B₁ correction procedure. MPnRAGE is demonstrated in phantoms and volunteers, including 2 volunteers with 8 scans each and 8 volunteers with 2 scans each. T₁ values from MPnRAGE were compared with those from fast spin echo inversion recovery (FSE-IR) in phantoms and a healthy human brain at 3T.

Results

The T₁ fit for human white and gray matter was T1_MPnRAGE=1.00 · T1_FSE-IR + 24 ms, r²=0.990. Voxel-wise coefficient of variation in T₁ measurements across 8 times points was between 0.02 and 0.08. ROI based T₁ values were reproducible to within 2% and agree well with literature values.

Conclusions

In the same amount of time as a traditional MPRAGE exam (7.5 minutes), MPnRAGE was shown to produce hundreds of images with alternate T₁ contrasts as well as an accurate and reproducible T₁ map that is robust to B₁ errors.

Introduction

Inversion-recovery prepared fast gradient echo methods such as magnetization-prepared rapid acquisition gradient echo (MPRAGE) (1) and similar implementations are widely used for high-resolution, T₁-weighted (T1w) neuroimaging applications. MPRAGE combines a spoiled-gradient echo (SPGR) readout with an inversion recovery (IR) preparation pulse to obtain high T1w signal contrast between white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF). In most MPRAGE acquisitions, the center of k-space is acquired shortly after the null point of CSF, providing good contrast between CSF and other tissues as well as moderate contrast between WM and GM. Contrast between WM and GM may be further improved using phase sensitive inversion recovery (PSIR) (2), a method that uses a separately acquired phase map to preserve the sign of the magnetization. In addition to T1w contrast from the inversion preparation pulse, traditional and phase sensitive MPRAGE acquisitions have weighting from T₂*, proton density, receiver sensitivity bias, and transmit B₁ field bias, which act to create spatially varying signal and reduced contrast between brain tissues. These extraneous factors decrease the diagnostic confidence and present challenges to automatic tissue-segmentation algorithms commonly used in neuroscience studies. A recent development, MP2RAGE (3), is a variation of MPRAGE that acquires two images, each at a different inversion time (TI), approximately doubling the scan time. A regularized division of the two complex images removes T₂*, proton density, and receiver sensitivity bias. When the appropriate TIs and other parameters are selected, the resulting images have reduced sensitivity to transmit B₁ and have higher contrast between WM, GM, and CSF.

A limitation common to all the methods above is that each one obtains only a single T₁ weighting with each acquisition (MP2RAGE acquires two images with different TIs, however the technique is optimized to obtain high T1w contrast in the combined image, and individual images tend to have low contrast). This may be problematic in certain situations, as T₁ values in the brain are known to be highly dependent on myelination and change with age or disease status (4). Therefore, any condition that affects myelination can produce suboptimal imaging results if the effects are not properly anticipated and accounted for in the acquisitions. Such conditions include dysmyelinating (e.g. Pelzus Mertzbacher disease) and demyelinating (e.g. multiple sclerosis) diseases, brain development (pediatrics) (5,6), as well as the aging brain (geriatrics) (7–9). Some of these conditions have unpredictable signal behavior and are patient specific, thus adjusting acquisitions for the changes a priori is challenging. Furthermore, pathological and natural changes in the developing and aging brain are region specific (5–9), so a single contrast setting may not be optimal across the entire brain.

One potential solution is quantitative T₁ mapping. Fast spin echo inversion recovery (FSE-IR) with a 3-parameter fit (10) to take into account inversion efficiency is considered by many to be a robust tool for T₁ mapping because it provides high quality images with low sensitivity to B₁ inhomogeneity. However, prohibitively long scan times prevent this method from being feasible for high resolution T₁ mapping of the entire human brain. Two-dimensional SPGR IR methods (11–15), commonly referred to as SNAPSHOT FLASH-IR (14) or Look-Locker (LL) (16,17), acquire several points along the IR curve in a single acquisition and may be used for T₁ mapping. The extension of these methods to 3D imaging (18) of large volumes with high spatial resolution is challenging, as spatial resolution and the number of images reconstructed along the relaxation curve are inversely related due to the Cartesian k-space sampling traditionally used. An alternative method for 3D T₁ mapping is to use an SPGR acquisition with two or more flip angles, a technique known as the variable flip angle (VFA) approach (19–21). This method is highly sensitive to B₁ errors, requires strong gradient spoiling (22,23), and requires simultaneous consideration of magnetization transfer effects for accurate mapping (24). Typically, B₁ errors are corrected using a separately acquired map, although one recent work used an additional IR image to correct for these errors (25). With careful selection of the acquisition parameters, MP2RAGE images have little sensitivity to the B₁ transmit field of the small alpha excitation pulses and the signal intensity and will be bijective (have a one-to-one relationship) with T₁ for brain tissue, allowing efficient T₁ mapping using a lookup table (3). However, dependence of T₁ on the efficiency of the inversion pulse remains, which may lead to T₁ underestimation if inaccurately accounted for in the lookup table (26). One work collected a third image along the IR curve (an MP3RAGE technique) with a different flip angle and determined T₁ with a non-linear search method incorporating inversion efficiency into the model (26).

Recently, we developed a novel method that combines inversion recovery preparation and 3D radial k-space sampling with vastly undersampled isotropic projection reconstruction (VIPR) (27) for a rapid gradient echo acquisition after each inversion (28). By repeatedly sampling the center of k-space at each gradient echo TR, the inversion recovery curve is finely sampled. Similar 2D techniques have been used for myocardial imaging (29), and another technique has used 2D steady state free precession (SSFP) inversion recovery for simultaneous T₁ and T₂ quantification in the brain (30). Weighted view sharing (27) of radial k-space lines with similar inversion times may generate images with high spatial resolution. This VIPR method with inversion recovery (VIPR-IR) enables the simultaneous acquisition and reconstruction of many 3D high-resolution, whole-brain images with different inversion time contrasts. By using similar processing to MP2RAGE (3), which takes a regularized ratio of two images acquired at different inversion times, it is also possible to generate high contrast T1w images without proton density, T₂* and receiver sensitivity bias and with reduced sensitivity to B₁ transmit-bias. Because VIPR-IR produces a practically arbitrarily large number of images n along the IR curve, where n is determined by the number of TRs (~300) and the retrospectively determined radial view-sharing window ω, our technique can be thought of as an MPnRAGE acquisition. Finally, the multiple inversion recovery images may be used to generate quantitative T₁ maps using the theoretical signal model. In this paper, we describe the MPnRAGE method and demonstrate several of its features including simultaneous acquisition of images with different inversion time contrast, T1w imaging with MP2RAGE processing, and quantitative T₁ mapping. The technique is demonstrated in T₁ phantoms, a healthy volunteer, and 10 volunteers who received multiple scans.

Theory

The original SNAPSHOT FLASH-IR experiment (14) was developed specifically for a Cartesian k-space acquisition. This model assumes that the image intensity is determined by the signal at the center of k-space. When radial imaging is used, every projection contributes to the center of k-space, violating the assumption of the SNAPSHOT FLASH-IR signal model. We therefore adapt the SNAPSHOT FLASH-IR signal model for radial imaging. Finally, we address challenges for accurate T₁ mapping using inversion recovery, such as incomplete recovery of longitudinal magnetization between successive preparation pulses and the presence of B₁ in-homogeneities of the radio-frequency (RF) pulses used for both the train of excitations in each SPGR block as well as the preparation pulse.

A schematic depicting the general acquisition is shown in Fig. 1. With all generality, the longitudinal magnetization is prepared with a β degree radio-frequency (RF) pulse. After a time TI from the center of the β preparation pulse, a series of N RF pulses with flip angle α are applied as in a standard spoiled gradient echo sequence. The next β RF preparation pulse is delayed by an amount of time T_D (the delay time) after the last α pulse to allow the longitudinal magnetization to freely recover. The expression for the measured signal M_n after the n^th (n = 0, 1…N − 1) alpha pulse is given by

$$M_n=M_{\infty }\left(1-{\stackrel{\sim }{M}}_0{a}^n\right)$$ [1]

Here is the steady state signal in the limit of n → ∞ and is given by

$$M_{\infty }=\rho \frac{1-E_1}{1-a}\sin \alpha$$ [2]

where $E_1=\exp (-\mathit{TR}/T_1)$, $a=E_1\cos \alpha$, and ρ is the product of the spin density, receiver sensitivities, and an exponential term $\exp (-TE/T_2^{\ast })$. The term ${\stackrel{\sim }{M}}_0$ is given by

$${\stackrel{\sim }{M}}_0=1-\frac{(1-a^{N-1})s}{1-s{a}^{N-1}}-\frac{[(1-E_D)E_I\cos \beta +(1-E_I)]}{1-s{a}^{N-1}}\frac{1-a}{1-E_1}$$ [3]

where $E_D=\exp (-\mathit{TR}/T_D)$, $E_1=\exp (-\mathit{TR}/T_I)$, and $s=E_D{E}_I\cos \alpha \cos \beta$. The recovery curve is exponential with modified relaxation time $T_1^{\ast }$ defined by the identity $a=\exp (-\mathit{TR}/T_1)\cos \alpha =\exp (-\mathit{TR}/T_1^{\ast })$.

Figure 1.

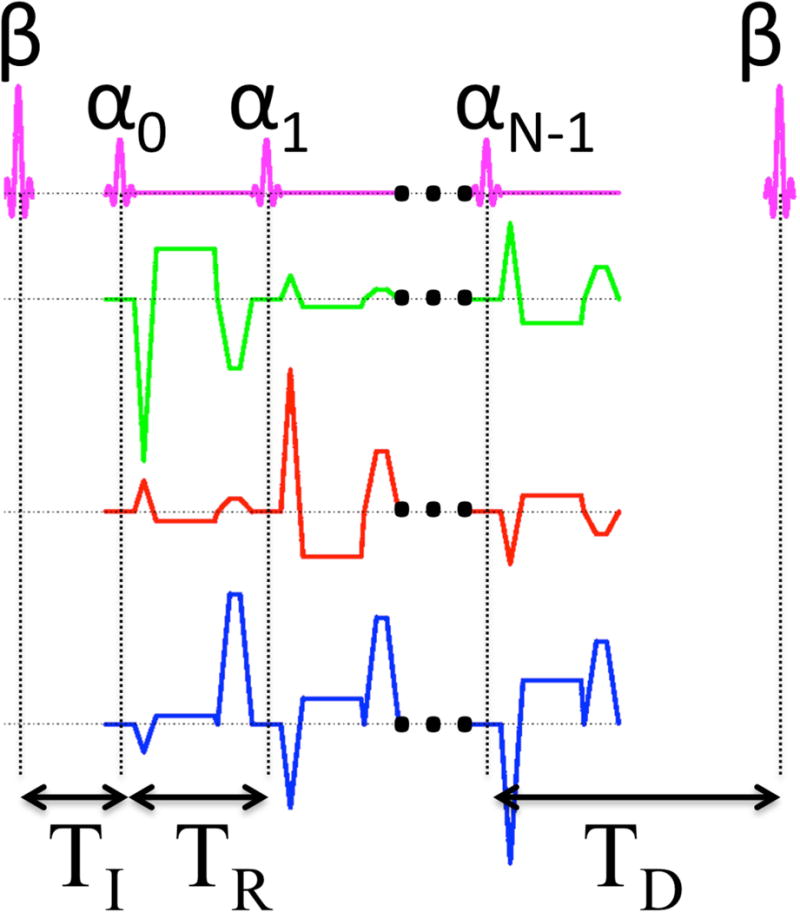
Diagram of the MPnRAGE sequence. A train of N RF pulses of flip angle α begins a time T_I after a preparation pulse of flip angle β prepares the magnetization. A delay time T_D allows the magnetization to freely regrow before the next preparation pulse is applied. Radial readout gradients are applied on all three axes, and a constant area spoiler is applied along the z-direction.

To reduce undersampling artifacts and increase the SNR, a sliding window reconstruction of width ω can be used that equally combines all projections starting at projection n (n = 0, 1, …, N −ω) after the β pulse up to and including projection n + ω − 1. This results in signal averaging in the central parts of k-space. Since image contrast is primarily determined by the central parts of k-space (31), the resulting image intensity is described by

$$M_n=M_{\infty }\left(1-{\stackrel{\sim }{M}}_{0}A{a}^n\right)$$ [4]

where the view-sharing amplitude modulator A is defined by A = (1−a^ω)/ω(1−a). It is a scale factor that takes into account the radial view-sharing and is determined by averaging Eq. 1 for all projections from n to n + ω − 1. The scale factor A reduces the initial value ${\stackrel{\sim }{M}}_n=0$, thereby reducing the dynamic range M_n=N−1 – M_n=0. Further reduction in artifacts as well as an increase in SNR may be achieved by gradually incorporating high spatial frequency components from projections that occur outside of the sliding window region (27). The effects of view-sharing radially interleaved k-space data across the IR curve was previously studied in (29).

When Cartesian sampling is used, the inversion time of an image is defined as the time from the center of the β pulse to the time when the center of k-space is acquired. For an image formed using a radial k-space acquisition and a sliding window of width ω, the effective inversion time is defined as the time from the center of the β preparation pulse to the time in the center of the sliding window. The effective inversion time for the n^th frame in the sliding window reconstruction is

$$T_{I,\mathit{eff}(n)}=T_I+\left[n+\frac{\omega -1}{2}\right]$$ [5]

When the longitudinal magnetization is allowed to fully relax between successive preparation pulses in a LL experiment, i.e., T_D ≳ (1 to 3)T₁ and several other conditions, including TR ≪ T₁ and β known (i.e. no RF inhomogeneities for the preparation pulse), T₁ can be efficiently estimated as in (14). If the longitudinal magnetization is not allowed to recover fully between successive inversions or the condition that TR ≪ T₁ is not satisfied, the full signal equation must be used to fit for the three unknowns ρ, T₁, and α (12). Kingsley (32) recently reported that even an adiabatic inversion pulse has efficiencies as low as 85% for the brain in vivo. When a perfect inversion is assumed, but not achieved, the three-parameter fit tends to underestimate T₁ (32). Simply fitting for the preparation angle β results in unstable approximation of T₁ (see Fig. 2). This is because an exponential recovery curve is defined entirely by three independent parameters (here, the starting position ${\stackrel{\sim }{M}}_{0}A$, the asymptote at infinity M_∞, and the rate $1/T_1^{\ast }$). To account for the additional unknown β, we combine inversion recovery data with separately acquired SPGR images at one or more flip angles. This allows a unique solution for ρ, T₁, κ and β to be found through the least squares minimization of combined IR and SPGR images, i.e. minimization of:

$$f(\rho ,T_1,\kappa ,\beta )={\displaystyle \sum _n\frac{1}{{\sigma }_n}{[M_n-S_{\mathit{IR},n}]}^2+\lambda {\displaystyle \sum _{j=1}^{N\alpha }\frac{1}{{\sigma }_j}{\left[\rho \frac{1-E_1}{1-E_1\cos \kappa {\alpha }_j}\sin \kappa {\alpha }_j-S_{\mathit{SPGR},j}\right]}^2}}$$ [6]

where the index n runs of all or a subset of inversion recovery images described by Eq. 4 for flip angle α = α_IRκ, N_α is the number of SPGR images, S_IR and S_SPGR are the measured signal intensities from the IR and SPGR acquisitions, and κ is a scaling factor between the actual and prescribed flip angle. The parameter λ controls the relative weighting between the IR and SPGR contributions. This is the extension of Eq. 7 of (25), generalized to account for the train of α pulses used in the SPGR radial inversion recovery experiment as well as an imperfect preparation pulse of arbitrary flip angle.

Figure 2.

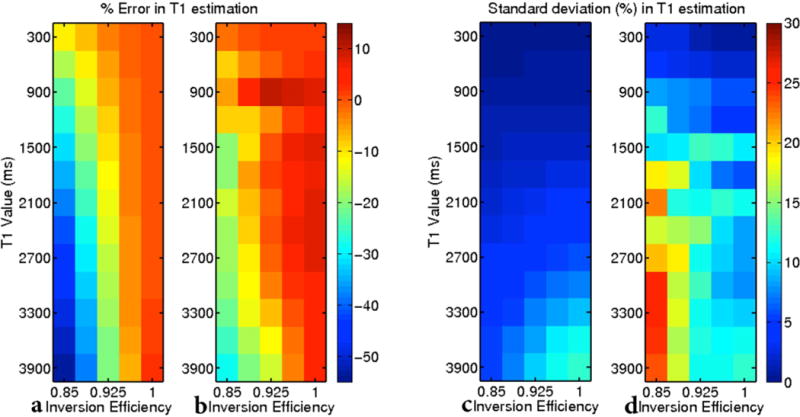
A three-parameter fit that assumes a perfect inversion even though one is not achieved largely underestimates T1 (a) but produces stable estimates (c). A four-parameter fit that includes a term for inversion efficiency reduces some error in T1 estimation (b), but produces an unstable fit (d).

Expanding the work of Deichmann (33) and references therein, we use a two-step procedure that improves T₁ fitting by using prior knowledge that the variations in the B₁ field and inversion efficiency should both be smooth. In the first pass, all four parameters (ρ, T₁, κ, β) are fitted to Eq. 6. The resulting κ and β maps are smoothed and then used as known values for a two parameter fit for.(ρ, and T₁) Reducing the number of degrees of freedom in the fitting procedure was previously shown to improve accuracy and precision (34) as long as sufficient prior information is available. Smoothing the κ maps is consistent with many other works (35–38), while smoothing the β is consistent with the success of (39).

T₁ quantification using Equation 6 requires a parameter λ that controls the contribution of SPGR images relative to IR images. Since the IR curve is fully defined by three parameters, fitting for the four unknowns should in principle only require three points along the IR curve and one extra SPGR image with different flip angle. An SPGR image at the same flip angle is insufficient since it is one of the three parameters determining the fit of the IR curve. The inclusion of a large number of inversion time points (~200) from an MPnRAGE acquisition has the potential to make the error contribution from a much fewer number (1 or 2) SPGR images in Eq. 6 negligible. One way to adjust for this is to compare the sum of squared signals (energy) of the IR and SPGR theoretical signals, derived using matching scan parameters and a range of expected T₁ values (i.e. the two terms of Eq. 6 with S_IR and S_SPGR both set to zero). To account for noise in the IR images, especially present in inversion times where WM and GM have very low signal, many previous IR methods report the use of additional points (~6 to 10 total) beyond the minimum three required for T₁ fitting. Analogously, this work selects λ so that the SPGR contribution in Eq. 6 is approximately ¹/₇ of the total contribution. For completeness, we have included a sensitivity map of λ performed using Monte Carlo noise simulations.

Methods

This section begins by providing details about the MPnRAGE acquisition and reconstruction that were not described in the background and theory section. Next it describes the phantom and in-vivo experiments that were performed to demonstrate features of the MPnRAGE method and to compare the T₁ values obtained with it to those from existing techniques.

Acquisition & Reconstruction

The acquisition order of radial projections is determined so that

1. Each point n along the recovery curve Eq. 1 contains samples located roughly angularly uniform across k-space.

2. Each point P = 0, 1,…, N − ω + 1 along the recovery curve Eq. 4 contains samples distributed approximately angularly uniform across k-space for arbitrary ω < N

3. Each subset of data consisting of projections acquired after two or more consecutive β pulses satisfies conditions (i) and (ii) above.

The first condition allows each point along the recovery curve Eq. 1 to be reconstructed when a sufficient number of preparation pulses have been acquired. When an insufficient number of samples are acquired and if condition (ii) is satisfied, view-sharing may be used to satisfy (i) and to improve image quality by reducing undersampling artifacts and increasing SNR. Allowing ω to be arbitrary is advantageous in the event that some subset of the data becomes corrupt or unusable (as in the event of motion, see below). This would allow the user to select the minimal ω needed to offer acceptable image quality while maximizing the dynamic range M_n=N−1 – M_n=0.

Although we will not address this issue here, condition (iii) will allow subsets of consecutive and motion free data from larger, motion-corrupt datasets, to form lower resolution navigator images that could later be co-registered to produce higher quality images as proposed in (40) and (41). Further, if the scan occurs after administration of gadolinium (Gd), the T₁ will change during the exam. Condition (iii) will produce k-space datasets with low spatial frequency weighting reflecting the average T₁ value (average Gd concentration) during the scan. This was used in our original implementation for cardiac imaging (28). When condition (iii) is not satisfied, unequal weights occur across the low spatial frequency components of k-space producing T₁ blurred images. Effects of interleaving projections with inconsistent data are discussed in (29).

General MPnRAGE acquisition parameters for all simulations, phantom, and in-vivo experiments are as follows: spatial resolution = 1.0 mm × 1.0 mm × 1.0 mm, whole head coverage (axial scans had slab thickness 160 mm and sagittal scans used non-selective RF excitation), TR = 4.6 to 5.0 ms, TE = 1.7 to 1.8 ms, nominal flip angle α_n = 4. Data acquisition begin between 10 to 42 ms after the center of the preparation pulse and occurred for approximately 1500 ms. The delay time T_D between the last RF excitation of each readout block and the next preparation pulse was approximately 500 ms. All exams took place on a 3T scanner (Discovery MR 750, GE Healthcare, Waukesha, WI). Axial acquisitions used the 8-channel GE receive-only head coil and sagittal acquisitions used the Nova 32 channel receive-only head coil (Nova Medical, Wilmington, MA). Scan time for the main IR component was fixed at 7.5 minutes.

Coil sensitivity maps are extracted directly from the radial imaging data (42) and used to combine the complex-coil images according to (43). This improves SNR and reduces undersampling artifact by reducing the effective FOV that determines the Nyquist sampling criterion to that of each coil’s sensitivity region. Furthermore, this process removes unwanted image phase, allowing restoration of the inverted signal (2). To reduce phase errors associated with the regrowth of the inverted longitudinal magnetization, only the views from the final MPnRAGE frame are used to create the sensitivity maps. When available, the SPGR image acquired at the end of an MPnRAGE quantitative T₁ exam can be used to extract the sensitivity maps.

MPnRAGE images were reconstructed with a 300 ms temporal window (ω ~ 60 frames). T₁ estimation is performed on a voxel-by-voxel basis using a two-pass procedure. In the first pass, the data were fitted on a voxel-by-voxel basis to Eq. 4 assuming ρ, T₁, κ and β as unknown variables. The κ and β flip angle maps were then smoothed with uniform kernels of size 4×4×4 and 8×8×8, respectively. The second pass used the smoothed values for κ and β maps as known parameters.

Parameters for the 2D FSE-IR sequence used for the in-vivo and phantom comparisons were: FOV = 256 mm × 192 mm, spatial resolution 2.0 mm × 2.0 mm, interpolated to 1.0 mm × 1.0 mm, slice thickness 5 mm, TR=15 s, TE = 7.34 ms, ETL=16, BW = 31.25 kHz, NEX = 0.5, 10 inversion times of T_I = [50 100 200 300 500 800 1000 1500 3000 4000] ms. T₁ fitting was performed on a voxel-by-voxel basis using a three parameter signal model that takes into account inversion efficiency.

Numerical Simulations

The accuracy and stability of T₁ fitting in the presence of RF inhomogeneity was investigated using numerical simulations. The first experiment tested what happens when an imperfect inversion pulse is applied and T₁ was estimated using (1) a 3-parameter fit assuming a perfect inversion and (2) a 4-parameter fit that takes into account inversion efficiency. Note that case (1) used

$$f(\rho ,T_1,\kappa )={\displaystyle \sum _n[M_n-S_{IR,n}]}$$

as the objective function, while case (2) used Eq. 6 with λ=0. Input IR curves were generated using Eq. 4 for T₁ values ranging from 300 ms to 3900 ms in increments of 300 ms. Additional parameters include a nominal value of α_n = 4°, actual value α_t = 0.95α_n, T_I = 20 ms, T_D = 508 ms, TR = 4.89 ms, N = 302, and ω=62. The input IR curves for each T₁ value were generated with 5 evenly spaced inversion efficiencies from ε = [0.85 to 1.00]. Gaussian noise was added so that an equivalent SPGR image with otherwise identical parameters would have an SNR of 125. A Monte Carlo noise simulation was then performed with 1024 independent noise realizations.

To test the accuracy and stability of T₁ estimations using Eq. 6 with additional SPGR images, a modified Monte Carlo noise simulation was performed. In this simulation, a flip angle (κ) map of the brain was first acquired in vivo using the Actual Flip angle Imaging (AFI) method (44). The flip angle map was then used to create a numerical phantom with homogeneous (16,663 pixels) T₁ value, but with a wide variety of representative κ values experienced in a human brain. This method was necessary since performing a Monte Carlo noise simulation for a wide range of T₁, λ, κ, and β values would be computationally demanding for a large number of independent noise realizations of each parameter pairing. Further, without having variations in κ, our two-pass fitting procedure would perform artificially well. Input IR curves were generated using Eq. 4 for T₁ values ranging from from 50 ms to 600 ms in increments of 50 ms and from 900 ms to 3900 ms in increments of 300 ms. The input IR curves for each T₁ value were generated with 5 evenly spaced inversion efficiencies from ε = [0.85 to 1.00]. T₁ fitting was performed using the IR data along with either a single SPGR image (nominal flip angle of 8°) and or two SPGR images (nominal flip angles of 6° and 10°). Gaussian noise was added so that an equivalent SPGR image with α_n = 4° and otherwise identical parameters would have an SNR of 125. Each T₁ phantom contained 16,663 voxels with independent noise realizations. The maximum value of the regularization parameter λ was determined so that sum-of-squares energy of the SPGR term was 1/3 the sum-of-squares energy of the IR term in Eq. 6.

The effect of the low spatial frequency k-space averaging on the ability to accurately estimate T₁ values was likewise investigated in a similar Monte Carlo experiment as above, this time changing ω, the amount of view-sharing, instead of λ. In this experiment, the regularization parameter λ was fixed based on the results of the previous experiment. The amount of view-sharing was varied from 50 ms to 600 ms in steps of 50 ms. All other parameters remained identical to the previously described experiment.

Phantom Studies

Phantom imaging studies were performed using three small tubes (60 mm diameter) containing water doped with CuS0₄ in concentrations of [37, 75, 225] μmols/L and 5 tubes containing water doped with Gd-BOPTA in concentrations of [0.10 0.25 0.50 1.0 and 2.0] mM. The phantoms with CuS0₄ concentration were designed to have T₁ values approximately that of WM and GM in a normal adult brain as well as an additional value well below the minimal T₁ value expected in a normal brain without contrast agent present. Quantitative T₁ mapping was performed using both MPnRAGE and 2D FSE-IR sequences. Two undersampled SPGR images were immediately acquired after the MPnRAGE exam with flip angles 6° and 10° and used for T₁ fitting in Eq. 6. Each SPGR image contained 16,046 projections and took approximately 75 seconds to acquire. The center slice of the MPnRAGE image was then imaged with the 2D FSE-IR acquisition described earlier.

Human Studies

Informed consent was obtained on all subjects and performed in compliance with protocols approved through the UW Institutional Review Board. All human studies used a 3T scanner (Discovery MR750, GE Healthcare, Waukesha, WI) and used the general MPnRAGE protocol described under the “Acquisition and Reconstruction” section. All T₁ fitting was performed on a voxel-by-voxel basis.

In Vivo Experiment 1

Qualitative comparison to Cartesian based MPRAGE and quantitative comparison to FSE-IR in a healthy adult male (27 years). Scans included a sagittal MPnRAGE acquisition that included two 75s SPGR images with nominal flip angles of 6 and 10 degrees, a 2D FSE-IR exam of a single axial slice, and a vendor supplied Cartesian based MPRAGE acquisition of the whole brain. The Cartesian based MPRAGE acquisition had the following parameters: FOV=256 mm × 256 mm, pFOV=0.91, slab thickness = 180 mm, acquired resolution =1.00 mm × 1.00mm × 1.00mm, TR=8.2 ms, TE = 3.2 ms, T_I =450 ms, α=15°, acquisition time 7.5 minutes.

The MPnRAGE T₁ map was co-registered to the FSE-IR T₁ map using a rigid body transformation using the software package FSL (45). Mean and standard deviations of T₁ were computed in several ROIs (shown in Fig. 6a and listed in Table 2). Linear regression using the mean T₁ values in each ROI was used to relate and compare the T₁ values of MPnRAGE with those from FSE-IR.

Figure 6.

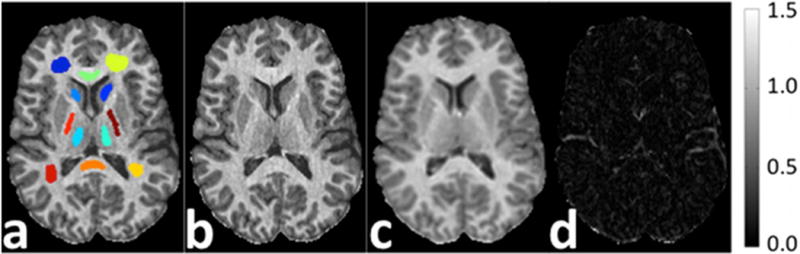
Figure (a) shows the ROIs for the R₁ maps in Table 1 (In Vivo Experiment 1). Quantitative R₁ maps in units of 1/s (b–c) from MPnRAGE and 2D FSE-IR as well as difference image (d).

Table 2.

T₁ measurements for select ROIs for In-Vivo Experiment 3 (reproducibility experiment 2) involving eight volunteers with two measurements each. The reported values in columns 2–3 reflect the mean +/− standard deviation of ROI measurements across all eight subjects. T₁ ROI measurements were determined from T₁ estimated calculated on a voxel-by-voxel basis. The reported absolute variability in column 4 reflects the mean +/− standard deviation of the absolute variability across all eight subjects. Absolute variability for each subject was calculated using T₁ ROI measurements.

	Scan 1	Scan 2	Absolute Variability	Literature
	T1 (ms)	T1 (ms)	%	T1 (ms)
WM CC genu	873 ± 35	875 ± 32	1.2 ± 1.1	919
WM CC splenium	906 ± 38	902 ± 47	1.7 ± 2.0	966
WM frontal	1025 ± 31	1025 ± 30	0.7 ± 0.6	1004
WM internal cap	943 ± 32	941 ± 41	1.0 ± 0.5	963
GM caudate	1502 ± 27	1491 ± 28	1.6 ± 1.2	1535
GM thalamus	1238 ± 31	1235 ± 44	2.8 ± 1.9	1344
GM putamen	1411 ± 23	1405 ± 21	1.1 ± 0.9	1372

In Vivo Experiment 2

Reproducibility of T₁ estimates on a voxel-by-voxel bases across eight time points in two subjects (M 44 years, F 46 years) with relapsing remitting multiple sclerosis. Each subject received eight axial MPnRAGE scans at one-month intervals. Each MPnRAGE scan also acquired a 90s SPGR image with nominal flip angle of 8 degrees used for T₁ estimation in Eq. 6. The coefficient of variation of the T₁ maps were computed on a voxel-by-voxel basis after aligning all T₁ maps to the initial T₁ map using the software package FSL (45). Spatial mean and standard deviations of the co-registered temporal T₁ mean image were computed in several hand-drawn ROIs. Only ROIs with normal appearing white and gray matter was used to test reproducibility.

In Vivo Experiment 3

Reproducibility of mean T₁ estimates of major WM and GM ROIs across two time points in eight adolescent (ages 12.9±0.6 years, 4F, 4M) subjects. Each subject received two MPnRAGE acquisitions spaced approximately 4 weeks apart. Each MPnRAGE scan also acquired a 90s SPGR image with a nominal flip angle of 9 degrees used for T₁ estimation in Eq. 6.

Subject-specific templates were produced by registering a T1w image from the second time point to the corresponding first time point of each subject using FSL (45). A study-specific template was then created from the subject-specific templates using the Advanced Normalization Tools (ANTS) software package (46). A final rigid transformation between this study-specific template and MNI template was determined using FSL. White and gray matter region-of-interest masks were defined using the MNI-atlas and warped back to the individual space of all subjects and time points. Mean T₁ values were calculated within all ROIs for each subject and time point. To decrease likelihood that neighboring tissues outside the ROIs (i.e. CSF) were included, histograms of all measurements were manually inspected for unexpected T₁ values and further erosion was performed as needed. The absolute variability (absolute value of percent difference) between mean ROI measurements of the two time-points was calculated for each subject. Each brain region was then analyzed separately by taking the mean, standard deviation, absolute variability, and standard deviation of absolute variability across subjects.

Results

Phantom Studies

The accuracy and precision of T₁ fitting using a 3-parameter fit and an assumed inversion efficiency of 1.0 are shown in Fig. 2(a,c), while the results of a 4 parameter fit of IR data to account for inversion efficiency are shown in Fig. 2(b,d). Accuracy of the 3-parameter fit dramatically decreases as the inversion efficiency decreases, with errors of −2%,−8%, and −17% when fitting for T₁ of 1200 ms and inversion efficiencies of 96.25%, 92.50%, and 88.75%, respectively. For a given inversion efficiency, the error increases with increasing T₁. The standard deviation of T₁ errors remains less than 5% across all inversion efficiencies for T₁ values below 2400 ms. While the magnitude percent error in T₁ estimation for a four parameter fit is similar to the three parameter fit, the 4 parameter fit is less stable as demonstrated by increased standard deviations across all T₁ values and inversion efficiencies. The minimum standard deviation for T₁ values 900 ms and larger is 6% and occurs at T₁=900 ms and a perfection inversion efficiency.

Figure 3 shows the results from the modified Monte Carlo simulation for the two-step T₁ fitting procedure of Eq. 6 that incorporates one (Fig. 3 a,c) and two (Fig. 3 b,d) SPGR images with alternate flip angles. For clarity, we only present the case with average inversion efficiency of 92.5%. However, the same general trends were observed across all inversion efficiencies, and the method showed little dependence on inversion efficiency. Increasing lambda tends to decrease percent error but increases variation. It should be noted that both effects are minimal (changes of order 1 to 2%), demonstrating the robustness of the technique to choice of lambda. Increasing T₁ tends to increase both error and variation. Again, both effects are minimal, especially for T₁ values of typical white matter and gray matter (changes on order of 1 to 2%).

Figure 3.

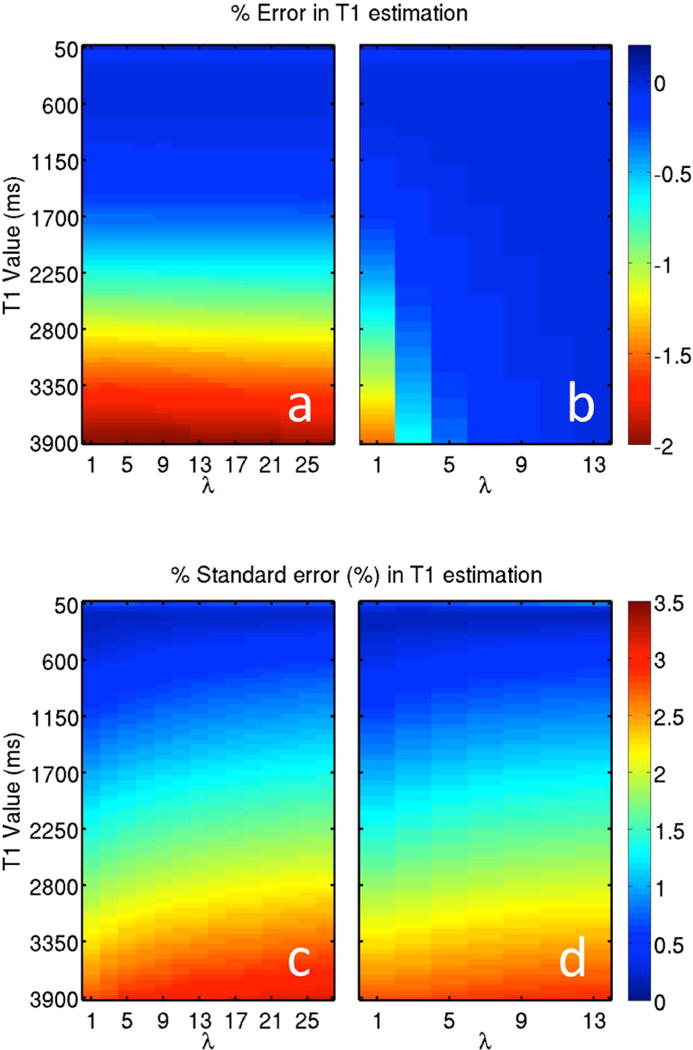
Including one (a,c) and two (b,d) SPGR images with different flip angles in a 4 parameter fit of IR data results in accurate T1 estimations with stable estimates. Using two SPGR images produces less error than using a single SPGR image. Both sets have little sensitivity to λ, which controls the relative weighting of SPGR to IR.

The effect of view-sharing on accuracy and stability of T₁ estimates is demonstrated in Figure 4. In general, the error and standard error increased as view-sharing increased for T₁>1700 ms when a single SPGR image was used. However, there was little variation (<0.1%) for shorter T₁ values and for the case when two SPGR images were used, except for the case where T₁=50 ms. When T₁ was 50 ms, error and standard error both increased with the amount of view-sharing and peaked at 2.2% and 1.3% (error) and 1.5% and 1.7% (standard error) for the case of 1 and 2 SPGR images respectively.

Figure 4.

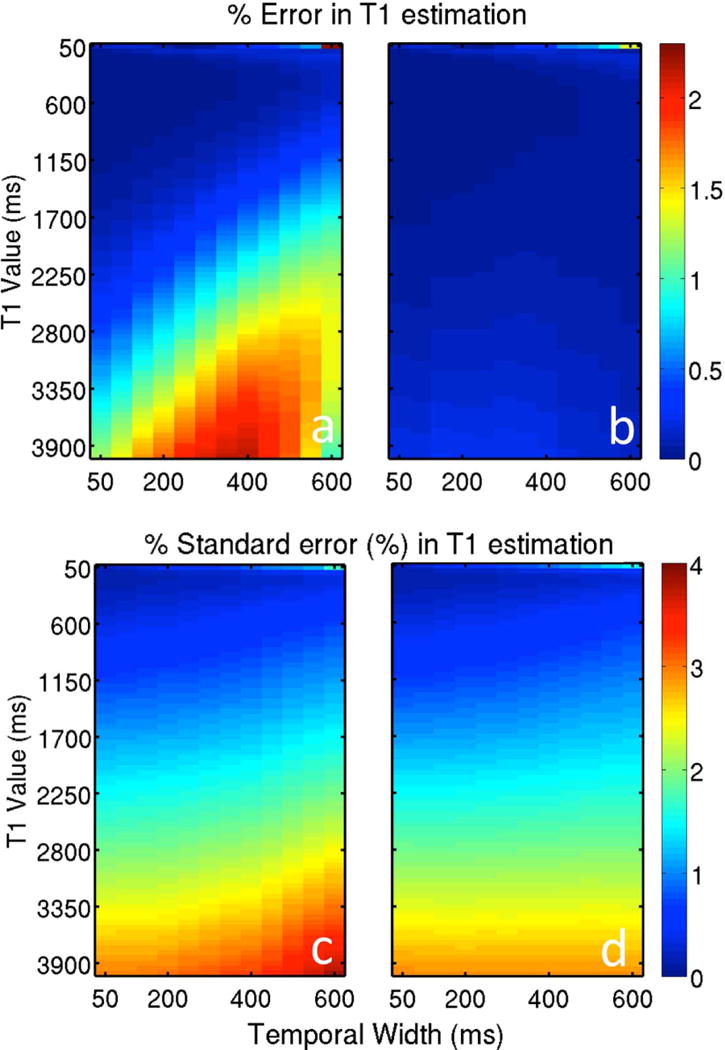
The effects of view-sharing (i.e. ω) on the error and standard error in T1 fits when (a) one and (b) two SPGR images are used in addition to the IR images.

The T₁ estimates from the phantom experiment are shown in Supplementary Table 1. The calibration curve between T₁ values estimates with MPnRAGE and FSE-IR is T1_MPnRAGE=0.91 T1_FSE-IR + 50 ms, r²=0.998 over the range of T₁ values from 91 ms to 2597 ms. The smallest and largest T₁ phantoms had the largest percent difference between the methods at −12% and 9%. When excluded from the calibration curve, the relation is T1_MPnRAGE=0.96 T1_FSE-IR + 22 ms, r²=0.995 over the range of T₁ values from 172 ms to 1261 ms.

Human Studies

In Vivo Experiment 1

Select images representing the variety of different T1w contrasts achievable from a single 7.5 minute MPnRAGE acquisition are shown in Fig. 5. The minimum (T_I,eff = 167ms) and maximum (T_I,eff = 1336 ms) effective inversion times produce little T1w contrast. Intermediate frames can selectively null white matter (frame 45), gray matter (frame 73), and cerebrospinal fluid (frame 118). Summing data across the entire inversion recovery curve produces a composite image with excellent T1w contrast and high SNR.

Figure 5.

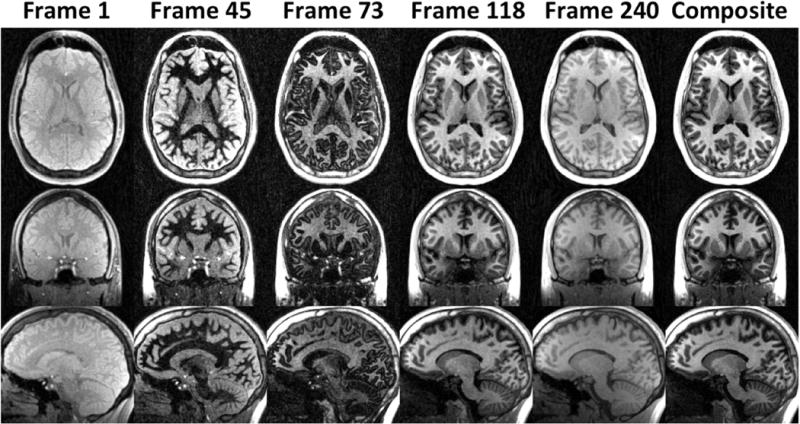
Example images from MPnRAGE displaying a variety of T1w contrasts. Frame 1: The earliest inversion time possible. Frame 45: Image with nulled white matter. Frame 73: Image with nulled gray matter. Frame 118: Image with nulled cerebral spinal fluid. Frame 240: The longest possible inversion time. Composite: image formed by summation of all the data.

A comparison of images obtained using the Cartesian based MPRAGE method and the approximately matched T1w contrast images from MPnRAGE are shown in Supporting Figure 1. The middle row are MPnRAGE images reconstructed by averaging the low spatial frequency contributions of the last half of the IR recovery curve, and result in similar T1w contrast to the Cartesian MPRAGE images (top row). In the bottom row, the MPnRAGE images have been intensity corrected by using the regularized division of a later inversion time by an earlier inversion time, as in Eq 3 of (3).

Figure 6 shows the quantitative R₁ maps from the comparison between MPnRAGE and 2D FSE-IR. The greatest differences occur at the boundaries of CSF and regions that suffer from inflow artifact. Results from the ROI analysis are shown in Table 1. The calibration curve had a slope of 1.00 (essentially identical), intercept of 24 ms, and r²=0.990.

Table 1.

T₁ measurements for select ROIs for In-Vivo Experiment 1 (comparison to FSE-IR) and In-Vivo Experiment 2 (reproducibility experiment 1). Measurements are were made over a single time point for volunteer 1 and across 8 time points for volunteer 2 to 3. The reported coefficient of variation C_v in the reproducibility experiment was calculated first on a voxel-by-voxel basis, then averaged across each ROI. The T₁ measurements for volunteer 1 provide the following calibration curve: T1_MPnRAGE=1.00 T1_FSE-IR + 24 ms, r²=0.990.

	Comparison to FSE-IR		Reproducibility Experiment 1
	Volunteer 1		Volunteer 2		Volunteer 3
	MPnRAGE	FSE-IR	MPnRAGE
	T1 (ms)	T1 (ms)	T1 (ms)	Cv	T1 (ms)	Cv
WM CC genu	861 ± 64	862 ± 68	811 ± 18	0.02	798 ± 25	0.05
WM CC splenium	881 ± 55	876 ± 32	825 ± 24	0.05	818 ± 28	0.06
WM ant left	909 ± 44	867 ± 20	912 ± 14	0.05	892 ± 47	0.05
WM ant right	892 ± 46	854 ± 19	880 ± 27	0.04	898 ± 56	0.06
WM post left	915 ± 50	886 ± 35	874 ± 21	0.05	906 ± 40	0.05
WM post right	924 ± 53	880 ± 30	845 ± 34	0.05	864 ± 28	0.05
WM internal cap left	923 ± 52	920 ± 36	864 ± 21	0.06	856 ± 31	0.07
WM internal cap right	927 ± 63	915 ± 30	870 ± 25	0.06	851 ± 44	0.07
GM caudate left	1301 ± 100	1293 ± 59	1276 ± 72	0.08	1238 ± 78	0.07
GM caudate right	1304 ± 139	1277 ± 84	1347 ± 66	0.08	1345 ± 68	0.08
GM thalamus left	1146 ± 90	1123 ± 47	1092 ± 36	0.06	1030 ± 38	0.07
GM thalamus right	1165 ± 109	1119 ± 54	1153 ± 72	0.07	1052 ± 80	0.08

In Vivo Experiment 2

The ability to visualize a small lesion in the cortical gray matter of a patient with MS is shown in Figure 7. For frames that occur after normal gray matter has reached the signal null (Fig. 7. a–f), the hypointense cortical lesion (yellow arrow) indicates an increase of T₁ at the lesion. For a magnitude image taken shortly after the null point of WM but before that of GM (Fig. 7 g–i), the hypointense GM adjacent to the lesion (blue arrow) indicates T₁ shortening. Fig. 7(j–l) are quantitative R₁ (1/T₁) maps. T₁ values inside the lesion range were 2200±200 ms (min/max is 1800 ms/2800 ms), while the normal appearing GM adjacent and left of the lesion has T₁ of 1226±35 ms. The GM adjacent and right of the lesion (blue arrow in Fig. 7i) has T₁ of 1140±10 ms, while gray matter to the right of the blue arrow in Fig. 7i has T₁=1224±35 ms.

Figure 7.

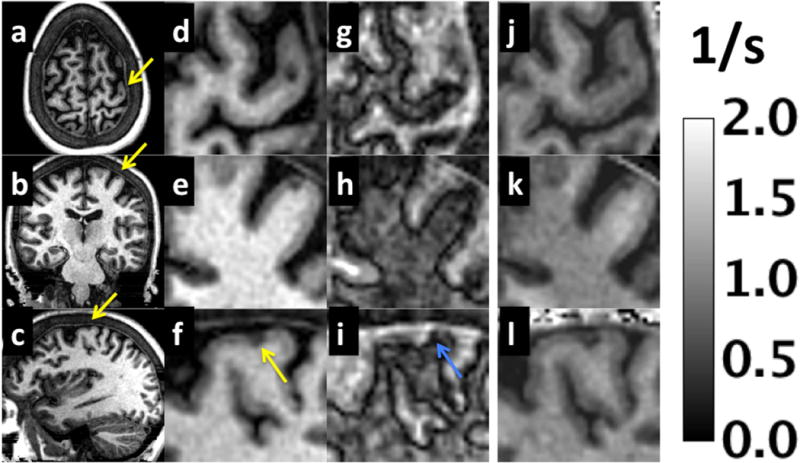
Example magnitude images from MPnRAGE for a patient with MS. Three cropped orthogonal views from the composite images are shown in (a–c) and in (d–f) for a zoomed region to depict a cortical gray matter lesion (yellow arrow). Zoomed images are also shown for an alternative contrast (g–i) that depicts a magnitude image when WM and GM have nearly equal magnitudes but opposite signs (WM > 0 and GM < 0) as well as quantitative R1 maps (j–l) in units of 1/s. The alternative contrast shows a region (blue arrow) just adjacent to the lesion that appears darker than both the lesion and surrounding normal GM.

Samples images, including the time-averaged T₁ maps and coefficient of variation maps are shown in Figure 8 for slices with normal appearing white and gray matter. The spatial mean and standard deviations of selected ROIs of the time-averaged T₁ map are shown in Table 1, along with the average coefficient of variation for T₁ of all pixels within each ROI. The coefficients of variation of T₁ maps across the eight measurements range from 0.02 to 0.08 for white and gray matter voxels.

Figure 8.

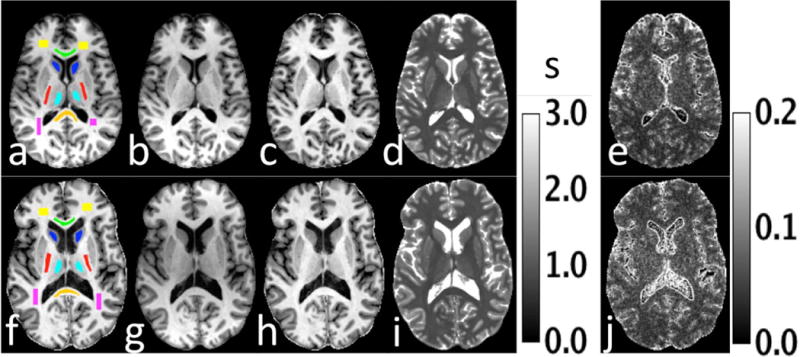
Figure 8 shows select axial images for two volunteers (a–e,f–j) with clinically definite multiple sclerosis who were scanned once a month for 8 months. Figure (a) shows the ROIs used for data analysis. The time-averaged composite images from MPnRAGE are shown in (b,c). Figures (c,h) are the time-averaged, intensity corrected images from MPnRAGE formed using a combination of high and low inversion time images. The time-averaged T₁ map is shown in (d,i), while the coefficient of variation of T₁ is shown in Fig. (e, j).

In Vivo Experiment 3

The mean and standard deviation of the overall absolute variability calculated across all ROIs and volunteers was 1.4±1.4%. The percent difference between the mean T₁ values of this experiment and published values (22) are within 2 to 8%. Detailed results of the region-of-interest reproducibility experiment are presented in Table 2 (volunteers 2 and 3) and Supplementary Table 2.

Discussion and Conclusions

In traditional implementations of MPRAGE utilizing Cartesian k-space readouts, there exists a 3-way tradeoff between spatial resolution, acquisition time, and the number of different T1w contrasts obtained in a single exam, where improvement in any two features results in worsening of the third. While more images along the relaxation recovery curve may be reconstructed by sampling the center of k-space more often, this means that either fewer high spatial frequency phase encoded lines will be acquired (decreased spatial resolution) or scan time will increase. Our proposed MPnRAGE method breaks the link between the number of T1w contrasts and acquisition time by using a radial k-space trajectory to acquire both low and high spatial frequency information with each TR. Instead of acquiring a single image with T1w contrast determined from a priori selection of the inversion time, a spectrum of 200+ images with different T1w contrasts may be acquired in a single exam. The large spectrum of images, which covers a wide range of T1w contrasts and enables subject-specific, optimized T1w contrast by allowing retrospective selection of the image or images that best depict anatomy and pathology on an individual basis. Additional uses for MPnRAGE have recently been proposed to provide tissue specific (i.e., WM- or GM- only) imaging (47), automatic GM/WM/CSF image segmentation (48), and retrospective motion correction (41) though these works are beyond the scope of this study.

We explicitly reconstructed all possible images with a fixed sliding window width as a proof of principle. We have also produced additional images by combining an image with a late inversion time with an image from an earlier inversion time as in Eq. 3 of (3). This technique removes weighting from spin density, T2*, and receiver sensitivity bias, reduces transmit B1 bias, and produces a high contrast T1w image (see Supporting Figure 1,g–i). With 300 images with different inversion times, there are about 45,000 (300 choose 2) different T1w contrasts (with 180 slices each) that could be produced with Eq. 3 of (3). It is unreasonable to send each volume for radiological examination or to store such a large dataset. A more thorough study will be needed to address the clinical utility of the extra information in the MPnRAGE images and will be presented in a future work. However, even in this preliminary study, we have demonstrated the ability of MPnRAGE to detect subtle changes in T₁. For example, in Fig. 6i, the lesion that has decreased T₁ values was visible at only 9 effective inversion times (between T_I,eff = 419 ms and T_I,eff = 459 ms). Note that the addition of T1w phase-sensitive inversion recovery images to T2w double inversion recovery images has been reported to improve the detection of cortical demyelinating lesions, which is currently a critical unmet need in MS imaging (49,50).

Although we have already begun to apply the method to detect subtle pathological changes from some of the “non-traditional” T1w images, such as T₁-shortening adjacent to the MS lesion (Fig. 7), a more comprehensive clinical evaluation is needed to determine the utility of the non-standard contrasts. Indeed, some groups have already begun investigating individually acquired alternative frames (TIs). Recently, groups have recently adjusting MPRAGE for WM nulling for improved cortical lesion detection (51,52)and delineation of the thalamic subnuclei (52). Other groups have begun investigating the GM/WM interface null frame to improve contrast between GM and intracortical GM lesions and to improve boundary identification between GM and juxta-cortical lesions (53) and to simplify tissue segmentation process in the brain (54). We believe that the tissue-specific nulling properties and computed images from multiple MPnRAGE frames provides a comprehensive new framework for diagnostic imaging and applications such as image segmentation and quantitative brain morphometry that will be significantly better than existing methods.

The protocols used in this paper were empirically designed to efficiently provide a large dynamic range (Fig. 5) for moderate T₁ signals such as white and gray matter signals, but not for large T₁ values such as cerebrospinal fluid. With a reduced dynamic range of signal, we do not expect the accuracy of such large T₁ values to be the same as small or moderate T₁ values. This was observed in the phantom results shown in Supporting Table 1 where the percent difference between T₁ estimates for MPnRAGE and FSE-IR was 9% for the phantom with mean T₁ value of 2597 ms. This difference is not surprising as neither the MPnRAGE or FSE-IR protocols were optimized for fitting of such large T₁ values. We found that the signal curves from the large T₁ phantom had such a small dynamic range that the signal curves nearly appear linear for both methods. The MPnRAGE protocol was also designed so that the main IR component was the same amount of time as a fully sampled MPRAGE exam (7.5 minutes). In order to reconstruct the individual inversion-time images with acceptable levels of undersampling artifact, 300 ms of view-sharing was used. As demonstrated in Eq. 4, view-sharing reduces the dynamic range of the magnetization recovery curve by increasing the signal at the first point (smallest T₁). While it may be somewhat surprising that 300 ms of view-sharing still produces accurate T₁ estimation at T₁=172 ms (3% difference compared to FSE-IR), the view-sharing effectively turned the inversion-recovery experiment into a saturation recovery experiment with the first point starting at 16% of the fully relaxed signal. Saturation recovery is widely used for rapid estimation of short T₁ value experiments (55). Meanwhile, the smallest phantom, which had mean T₁ of 92 ms had the first point start at over 50% of maximum signal. We expect that protocols for estimation of large T₁ values could be designed by increasing the amount of the relaxation curve that is sampled, and that protocols for estimation of smaller T₁ values could be designed by decreasing the amount of view-sharing used in the reconstruction. The design of such protocols is beyond the scope of this paper.

Like almost all methods using a non-linear search over multiple variables, the initial estimates and stopping criterion are important for robust fitting. A nice advantage of the multiple inversion frames provided by MPnRAGE is the ability to convert the null-frame index (i.e. the frame at which the signal nulls) to T₁ using a lookup table created using assumed B₁ errors (κ=1 and β=150). This in turns produces reasonable estimates for the spin-density factor ρ. We found that the objective function used for T₁ estimation can be rather flat, especially at large T₁ values. Thus, fitting may be sensitive to search methods and stopping criterion, especially for large T₁ values like those found in CSF.

While we have used radial k-space trajectories to collect both low and high spatial frequency information with each TR, there are a number of alternative trajectories that could be used such as the cones trajectory (56), rotated spiral readout (57), or the radial cones trajectory (58). In this work, we have relied on angular undersampling and a complex combination of individual coil images using coil sensitivity maps (43) to provide the necessary acceleration. However, the serial set of images along the magnetization relaxation recovery curve generated by our MPnRAGE technique are well suited for compressed sensing methods utilizing a parametric dimension to perform model-based reconstruction (59,60) and sparsity promoting regularization (61). We suspect that these methods would improve existing image quality by reducing artifacts due to undersampling and sliding window combination, and could reduce acquisition time and/or increase spatial resolution. However, the implementation of these methods is beyond the scope of this initial work.

In conclusion, in this work we introduced a new 3D method that simultaneously acquires a standard T₁ weighted MPRAGE-like image in addition to a serial set of automatically co-registered images with multiple IR contrasts in about the same amount of time as a fully sampled traditional MPRAGE with Cartesian k-space readout. Modifications to the analytical expression describing the MR signal along the IR curve were made to account for radial view-sharing used in the reconstruction process. A rapid new B₁ calibration approach was presented that combined IR images with steady state SPGR images with different flip angles to correct for inhomogeneities of both the excitation and preparation pulses. T₁ values obtained both in phantom and in vivo agreed well with FSE-IR. One reproducibility experiment involving two individuals who each received 8 monthly scans showed the coefficient of variation of T₁ for normal appearing white and gray matter was measured is between 0.02 to 0.08. A second reproducibility study involving 8 volunteers with two times points showed that the absolute variability (in %) of ROI based T₁ measurements is 1.4±1.4 when averaged across all ROIs of all subjects. Both reproducibility studies suggest that MPnRAGE provides a highly reproducible measure of T₁. T₁ measurements of 7 major WM and GM areas averaged across 8 subjects (with 2× time points) were within 2 to 8 % of published literature. In at least one case, a non-traditional contrast from MPnRAGE was used to detect subtle differences between tissues with similar T₁ values as well as for T₁ quantification. The availability of high resolution multidimensional data (3 spatial and one T1-w dimensions) as well as quantitative T₁ maps from the same scan may prove useful in providing additional reference images for radiologists to detect pathology and for morphometric applications.

Supplementary Material

Supp TableS1-S2 & FigureS1

Supporting Table 1: T₁ measurements in Phantom.

Supporting Table 2: Percent differences (scan 1 – scan 2) for T₁ measurements for each subject from In-Vivo experiment 3. The values reported in column 2 reflect the percent differences averaged across all ROIs within each subject.

Supplementary Figure 1: Example T₁-weighted images from Cartesian MPRAGE (a–c), and radial MPnRAGE (d–i) for a normal volunteer. The images in the middle row (d–f), are produced using low spatial frequency information from only the last half of the inversion recovery curve and have similar contrast as in the Cartesian technique. The images in the bottom row have been intensity corrected by taking the regularized ratio of an early inversion time by a late inversion time and have had a background mask applied.