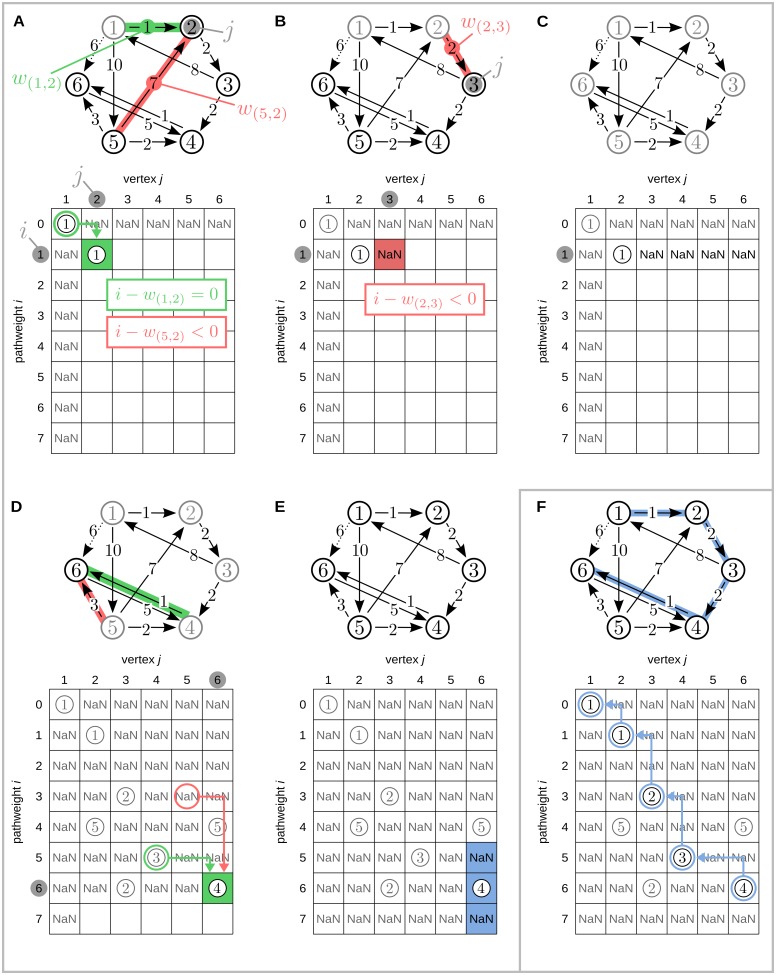
Fig 6. Visualization of the proposed algorithm.

Search for alternative paths to edge (1, 6) (dotted arrow), i.e., v _s = 1 and v _t = 6. Solutions ${\mathbf{L}}_{v_s}^n(w_i;⇝v_j)$ to subproblems are managed in a two dimensional solution array indexed by path weight w _i and vertex number v _j. Solutions are calculated iteratively over w _i (rows) and v _j (columns). (A) Solution matrix after first iterative step (subproblem ${\mathbf{L}}_{v_s}^1(1;⇝v_2)$): There are two edges leading to vertex 2 of which only edge (1, 2) yields a valid solution by pointing to an earlier solved subproblem (green box), whereas edge (5, 2) has a weight of 7 leading to a negative difference in weights i − w _(5,2) (red box) for which no earlier solution exists; (B) Solution matrix after third iterative step ${\mathbf{L}}_{v_s}^3(1;⇝v_3)$: Here, no valid solution exists (none of the arrows leading to vertex 2 are part of a path with summed weight 1); (C) Solution array after iteration over all vertices v _j for w _i = 1 (all vertices have been checked for a path of weight 1, originating from the start vertex 1); (D) Solution to subproblem ${\mathbf{L}}_{v_s}^n(6;⇝v_6)$: edge (4, 6) together with the solution ${\mathbf{L}}_{v_s}(5;⇝v_4)$ form a valid path, whereas edge (5, 6) is not part of a valid solution as ${\mathbf{L}}_{v_s}(3;⇝v_5)$ is empty; (E) The algorithm terminates after iteration over all vertices v _j and path weights up to w _{(vs, vt)} + θ, where θ is a user defined threshold of 1. Backtracking is conducted for all entries in the reconstruction interval w _{(vs, vt)} ± θ (entries marked blue); (F) Reconstructed alternative path by backtracking of subproblems.