Support for linguistic macrofamilies from weighted sequence alignment

Significance

This article reports findings regarding the automatic classification of Eurasian languages using techniques from computational biology (such as sequence alignment, phylogenetic inference, and bootstrapping). Main results are that there is solid support for the hypothetical linguistic macrofamilies Eurasiatic and Austro-Tai. Unlike comparable previous work, these findings do not depend on manual assessments of etymological facts. This study contributes to ongoing efforts to push the limits of linguistic reconstruction further back in time, and thus to open a window into the pre-Neolithic human past. The methodological approach pursued here can be seen as a statistically informed and automatized version of Joseph Greenberg’s mass lexical comparison, which yielded intriguing results regarding deep genetic relations between languages but has remained controversial among experts.

Abstract

Computational phylogenetics is in the process of revolutionizing historical linguistics. Recent applications have shed new light on controversial issues, such as the location and time depth of language families and the dynamics of their spread. So far, these approaches have been limited to single-language families because they rely on a large body of expert cognacy judgments or grammatical classifications, which is currently unavailable for most language families. The present study pursues a different approach. Starting from raw phonetic transcription of core vocabulary items from very diverse languages, it applies weighted string alignment to track both phonetic and lexical change. Applied to a collection of ∼1,000 Eurasian languages and dialects, this method, combined with phylogenetic inference, leads to a classification in excellent agreement with established findings of historical linguistics. Furthermore, it provides strong statistical support for several putative macrofamilies contested in current historical linguistics. In particular, there is a solid signal for the Nostratic/Eurasiatic macrofamily.

The established comparative method of historical linguistics has been immensely successful in reconstructing the history of human languages, far beyond the limits of written records. It established over 200 families [according to Glottolog’s classification scheme (1)], mostly having an estimated time depth of several millennia.

The scope of this method, according to a near-consensus in the field, is intrinsically limited to a time depth of ∼10,000 y, however. Over the past century, there have been an abundance of proposals for macrofamilies going back further in time. Few of these proposals are currently backed up by evidence as strong as is required by the professional standards of historical comparative linguistic research. These professional standards demand reconstruction of a substantial portion of the protolanguage’s vocabulary and grammar plus the historic processes leading to its attested descendants, which are vetted and approved by the scholarly community via peer review. So far, Afro-Asiatic is arguably the only macrofamily coming close to meeting these criteria; all other proposals along those lines are currently hypotheses at best, with varying degree of empirical justification. Perhaps the most intensely discussed such proposal concerns the Eurasiatic macrofamily (2, 3), comprising a large portion of uncontroversial families from Eurasia. A recent statistical study by Pagel et al. (4) estimated its time depth at 14,450 y.

The study by Pagel et al. (4), as well as other recent applications of phylogenetic methods to historical linguistics (5–7) (for critical assessments see refs. 8 and 9), bases its inference on expert cognacy judgments. These judgments are largely consensual within accepted language families but necessarily controversial beyond that limit. Therefore, the findings of Pagel et al. (4) have sparked a fair amount of critical discussion among historical linguists (e.g., 10). Grammatical classifications (11, 12) are an alternative to cognacy data; they are also available only on a relatively small sample of languages in sufficient detail at this time.

To sidestep this issue, the present investigation pursues a purely data-oriented approach not reliant on expert judgments. It is based on data from the Automated Similarity Judgment Program (ASJP; data are available online at asjp.clld.org/static/listss16.zip) (13). This database comprises translations of 40 basic concepts for more than 6,000 languages and dialects, covering more than two-thirds of the world’s living languages. Each entry is given in a uniform phonetic transcription.

In this study, I zoomed in on the 1,161 doculects (languages and dialects) from the Eurasian continent (including neighboring islands but excluding the predominantly African Afro-Asiatic family and the predominantly American Eskimo-Aleut family, as well as the non-Asian parts of Austronesian) contained in the ASJP database. In a first step, pairwise similarities between individual words (i.e., phonetic strings) were computed using sequence alignment. In a second step, these string alignments were used to determine pairwise dissimilarities between doculects. Briefly put, the dissimilarity between two word lists is a direct measure of how likely it is that the degrees of similarity between the elements of the two lists could have arisen by chance alone [details on this method of distance calculation are provided in my previous work (14) and are discussed in Materials and Methods]. These dissimilarities served as input for distance-based phylogenetic inferences [using the greedy minimum evolution algorithm, combined with balanced nearest-neighbor interchange postprocessing (cf. 15)].

The resulting phylogenetic tree is in excellent agreement with the expert classification from Glottolog (1) [as supplied by the ASJP database; generalized quartet distance (16) is 0.005.] To assess the reliability of this tree, the degree of statistical support was determined for each clade. These confidence values were estimated using a Bayesian version of the bootstrap interior branch test (17) (Materials and Methods; the tree annotated with confidence values is supplied in Dataset S1).

Generally, the Glottolog classification is strongly supported by this method. Only three Glottolog families have a confidence value $<100\text{\%}$: Dravidian (0.998), Indo-European (0.860), and Sino-Tibetan (0.995).

The relatively low support seen for Indo-European is due to a number of rogue taxa (i.e., doculects whose base vocabulary word lists contain conflicting information). An example of data containing conflicting information is provided by the English word list. It contains the entry maunt3n “mountain,” which is similar to its counterpart in the Romance languages, but not in the other Germanic languages, whereas most other entries for English are more similar to their Germanic counterparts than to their Romance counterparts.

To detect those inconsistencies in word lists, Cronbach’s alpha, a measure of consistency between different variables, was computed for each word list. [Cronbach’s alpha has been suggested as a way to validate word-based methods for comparing dialects (18), and the argument carries over to cross-linguistic data. It ranges from 0 to 1, where 0 means “totally inconsistent” and 1 means “fully consistent.”] Most values are fairly high (mean of 0.82 and median of 0.84), indicating that despite the rather small number of only 40 items per word list, the similarity values for these 40 items provide a detectable signal. For 58 word lists (i.e., $5\text{\%}$ of all data), Cronbach’s alpha is $<0.6$. These word lists include the language isolates Basque, Burushaski, Korean, Kusunda, Nahali, and Shom Peng, as well as all Kartvelian and Abkhaz-Adyghe doculects. Among the Indo-European doculects, Gheg Albanian, Greek, Manx, and Scottish Gaelic fall within this group. The full list of excluded doculects is provided in SI Rogue Taxa.

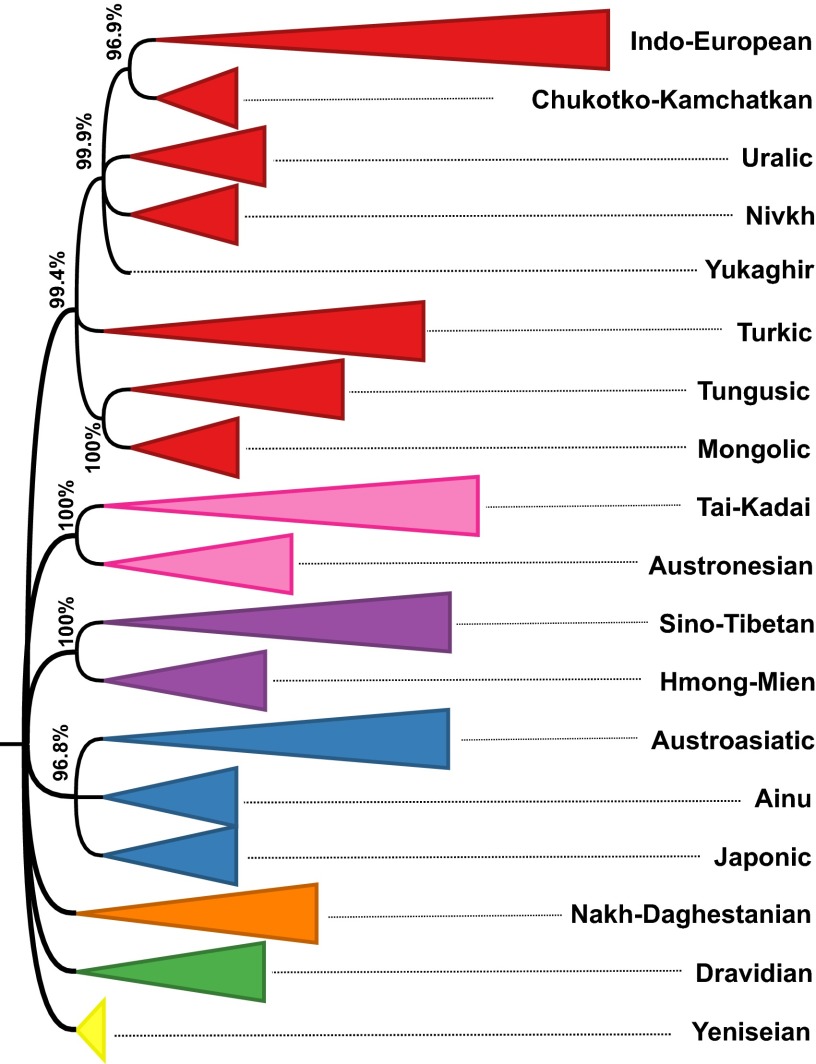
The same analysis as detailed above was carried out using the 1,103 doculects with an alpha value $\ge 0.6$. The resulting phylogenetic tree (Dataset S2) is again in excellent agreement with the Glottolog expert classification (generalized quartet distance = 0.005, all mismatches occur within language families). The confidence values for the Glottolog families is invariably high [Indo-European, 0.967; Sino-Tibetan, 0.983; Uralic, 0.985; and all other families, 1.000]. The phylogenetic tree above the level of families is depicted in Fig. 1. All nodes with support below 0.95 are collapsed (the full tree is supplied in Dataset S3.).

Fig. 1.

Phylogenetic tree above the level of Glottolog language families. Numbers at nodes are confidence values. Colors indicate top-level taxa.

Discussion

The tree contains seven taxa above the family level. Before discussing them in detail, let me add some general considerations on the interpretation of the automatically generated phylogeny.

Generally, a lower than average distance between two word lists may be due to three factors: (i) common descent, (ii) language contact, or (iii) chance similarities (which may or may not be due to universal tendencies in sound and meaning association, such as onomatopoeia or nursery forms).

The fact that the automatically generated tree is in such good agreement with the Glottolog classification demonstrates that this method is sensitive to common descent. The interesting question is to what degree it is also sensitive to language contact and chance similarities.

To start with the latter, the data contain at least one group of cases where chance similarities affect phylogenetic inference and confidence values. There is a surprisingly high number of resemblances between Celtic and Chukotko-Kamchatkan words; they are listed in Table 1. These similarities are not shared by other Indo-European languages, so they cannot be explained as deep cognacy. Likewise, there is no plausible scenario explaining these similarities as loans.

Table 1.

Chance resemblances: Celtic and Chukotko-Kamchatkan (CK) words

Meaning	Celtic language	CK language	Celtic word	CK word
Skin	Breton	Koryak	korxEn	x3lx3n
Skin	Breton	Alutor	kroxEn	x3lx3n
Stone	Irish Gaelic	Northern Itelmen	klox	kox
Stone	Welsh	Northern Itelmen	karEg	kox
Path	Manx	Chukchi	red	ret
Skin	Manx	Alutor	krax3n	x3lx3n
Skin	Manx	Chukchi	krax3n	x3Lx3n
Skin	Manx	Koryak	krax3n	x3lx3n
Stone	Manx	Northern Itelmen	klax	kox
Stone	Scottish Gaelic	Northern Itelmen	klax	kox
Louse	Scottish Gaelic	Alutor	mi3l	m3m3ll3
Louse	Scottish Gaelic	Chukchi	mi3l	m3m3l
Louse	Scottish Gaelic	Koryak	mi3l	m3m3l
Louse	Scottish Gaelic	Northern Itelmen	mi3l	m3lm3l
Louse	Scottish Gaelic	Southern Itelmen	mi3l	m3lm3l

Rows below the line involve rogue taxa.

Excluding these word pairs from the analysis has a substantial impact on the analysis. In particular, the confidence value for Indo-European rises from 0.860 to 0.957.

However, 11 of the 15 chance resemblances listed in Table 1 involve the rogue taxa Manx or Scottish Gaelic (alpha values are 0.57 and 0.55, respectively). In the reduced dataset, the remaining four pairs have only a minor impact; excluding them does not change the topology of the tree and only mildly affects confidence values. The confidence value rises from 0.967 to 0.981 for Indo-European, and it falls from 0.969 to 0.964 for the Indo-European/Chukotko-Kamchatkan clade.

Two points are noteworthy here: (i) The mentioned chance similarities led to a massive reduction in confidence for a genetically valid clade, Indo-European, but did not lead to the formation of any high-confidence invalid clades (e.g., Celtic + Chukotko-Kamchatkan), and (ii) low values for Cronbach’s alpha are a good indicator for such chance similarities, as restricting the analysis to doculects with high alpha values reduces the impact of chance.

Similar observations can be made with regard to clear cases of language contact. Even though borrowing of core vocabulary is less common than in other strata of the lexicon, it does occur quite frequently (19). If an ASJP list contains several loans from distantly related or unrelated languages, this configuration will lead to a low alpha value. An example might be the Sino-Tibetan language Northern Tujia. Its word list displays several high similarities to corresponding entries from non–Sino-Tibetan languages (e.g., Northern Tujia luka vs. Mangshi Tai/Tai-Kadai luk “bone,” Northern Tujia Sipuli vs. Santali/Austroasiatic ipil “star,” Northern Tujia aN vs. Eastern Katu/Austroasiatic 5aN “we”) that are possibly loans. The alpha value for Northern Tujia is as low as 0.34; therefore, this language is excluded from the analysis.

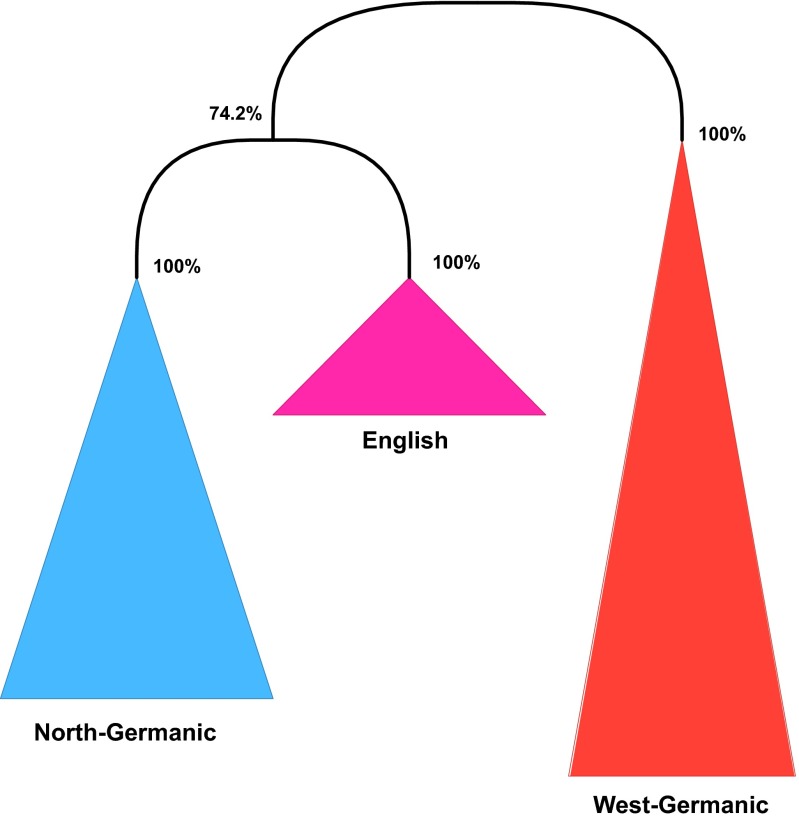
We observe a different effect if borrowing occurs between closely related languages. The Scandinavian influence on English (reflected in loans; e.g., “skin,” “to die”) obscures its West Germanic affiliation, although its alpha value remains high at 0.86. As a result, English (alongside with Scots) appears as a sister clade of North Germanic in the phylogenetic tree, but this connection has a low confidence of $74.2\text{\%}$ (Fig. 2), whereas both West Germanic and North Germanic proper have $100\text{\%}$ confidence values. Therefore, English would be considered as unaffiliated within the Germanic subfamily. Here, the effect of language contact blurs the phylogenetic signal for the borrowing language, whereas the position of its genetic relatives and the borrowing source are not affected.

Fig. 2.

Germanic subfamily.

Contact can have a more severe impact on the phylogenetic signal if (i) a large portion of a genetic unit is affected and (ii) the effect of contact is not in conflict with the signal resulting from inherited words. The relation between the Hmong-Mien and Sino-Tibetan language families might be a case in point.

The word lists for Hmong-Mien doculects contain a substantial number of likely Sino-Tibetan loans. Of the 1,018 word entries for extant Hmong-Mien languages contained in the database for which the database also provides translations into Proto-Sino-Tibetan and Proto-Hmong-Mien, only 71 have an uncalibrated string similarity $>0$ to their Proto-Hmong-Mien counterpart. A nonnegative similarity score indicates that the similarity is higher than chance (compare Materials and Methods for details on the string similarity measure), whereas 182 entries have a similarity score $>0$ to their Proto-Sino-Tibetan counterpart. This pattern suggests that a considerable portion of the extant Hmong-Mien vocabulary is ultimately of Sino-Tibetan origin and was borrowed into (perhaps earlier stages of) Hmong-Mien. In fact, Southeast Asia is known to be a linguistic area with a long history of extensive language contact (20).

The Sino-Tibetan influence affects the entire Hmong-Mien family. Also, Hmong-Mien is not part of another language family, so language contact does not lead to inconsistent patterns here; the mean alpha value for the 34 Hmong-Mien doculects is 0.73, and only three of them have an alpha value $<0.6$. Consequently, phylogenetic inference combines Sino-Tibetan and Hmong-Mien to one taxon with a confidence value of $100\text{\%}$.

This discussion suggests three things: Chance similarities have little impact on the shape of the phylogenetic tree (i) because most instances either lead to a drop of the alpha value for at least one of the affected doculects below the threshold of 0.6 or (ii) because they induce reduced confidence scores without actually affecting the topology of the phylogenetic tree, and (iii) the same holds for unsystematic borrowings that only affect individual languages if the borrowing language is part of a larger genetic unit. Systematic and sustained language contact affecting an entire genetic unit without strong outside genetic ties does affect phylogenetic inference; it may lead to high-confidence clades not corresponding to a common ancestor.

As a disclaimer, it should be stressed that these considerations are based on plausibility arguments and anecdotal evidence at this point. A systematic quantitative investigation would require gold-standard data annotated for cognacy vs. borrowing vs. chance resemblance. Unfortunately, such data are currently unavailable at the required scale.

With these considerations taken into account, let us return to the seven suprafamily clades in Fig. 1:

• i)Japonic + Ainu + Austroasiatic: Some scholars (21, 22) argue that Ainu is connected to Austroasiatic at a deep level, possibly as part of an even larger Austric macrofamily (additionally including Austronesian and Tai-Kadai). If true, this fact would account for a clade comprising Ainu and Austroasiatic; the association with Japanese is arguably due to its contact with Ainu.
• ii)Hmong-Mien + Sino-Tibetan: As discussed above.
• iii)Austronesian + Tai-Kadai: A macrofamily comprising these two languages has been argued for repeatedly in the literature (23, 24).
• iv)Chukotko-Kamchatkan + Indo-European + Mongolic + Nivkh + Tungusic + Turkic + Yukaghir + Uralic: Except for the exclusion of Ainu and Japonic, this clade is coextensive with Greenberg’s (2, 3) Eurasiatic proposal (to the degree that it overlaps with the languages considered here). This proposal for a linguistic macrofamily, as well as the closely related Nostratic hypothesis (25), is highly controversial among experts (as discussed, inter alia, in the contributions in Salmons and Joseph's collected volume, ref. 26).
• v)Mongolic + Tungusic: These two families are frequently considered part of the macrofamily (core-) Altaic along with Turkic. The Altaic proposal is controversial as well; Georg et al. (27), e.g., defend this hypothesis whereas Janhunen (28) assesses most evidence marshalled to its support as invalid. Remarkably, Mongolic, Tungusic, and Turkic do form a clade in the full tree, but its confidence value is only 0.908, as opposed to 1.000 for Mongolic + Tungusic. According to Janhunen (28), the case for Mongolic and Tungusic forming a genetic unit is stronger than for Altaic as a whole.
• vi)Chukotko-Kamchatkan + Indo-European + Nivkh + Yukaghir + Uralic: The idea of such a core-Eurasiatic unit has been argued for by Kortlandt (29). [Kortlandt also includes Eskimo-Aleut into this group (29), which is not considered here.]
• vii)Chukotko-Kamchatkan + Indo-European: Even proponents of Eurasiatic do not consider Chukotko-Kamchatkan as Indo-European’s closest relative. So, from the point of view of Eurasiatic/Nostraticist scholarship, the status of this clade is doubtful. It may be a remnant of a more inclusive clade that has been diluted by language contact and the decay of inherited vocabulary (akin to the West-Germanic clade in Fig. 2, which incorrectly excludes English) or may reflect language contact.

To conclude, most high-confidence deep clades in the automatically generated tree correspond to proposals for deep genetic relationships in the literature. The results presented here provide further evidence for proposals such as Austro-Tai, Mongolic + Tungusic, and Euroasiatic.

Let me summarize. Phylogenetic inference based on string comparison of short word lists very reliably identifies monophyletic linguistic units up to the level of language families [even though the prospects of such an endeavor have been assessed skeptically in the literature (cf. 30)]. All Glottolog families are correctly identified with a confidence at or close to 100%. Furthermore, the method identified several suprafamily clades that partially correspond to proposals for deep genetic units that have been arrived at by different means. These findings provide additional evidence for deep historical relations between the language families in question.

However, there is no principled way to factor common inheritance from diffusion with this method. To tackle such questions, a computational and statistical approach requires more linguistically informed stochastic models that explicitly address such issues as cognate recognition, identification of regular sound laws, protoform reconstruction, and competing processes of inheritance and diffusion. Efforts to this effect are already under way [i.e., for automatic cognate recognition and multiple word alignment (31, 32), for automatic protoform reconstruction and identification of sound laws (33, 34), and for an explicit model of lexical borrowing (35)]. The present work is designed to contribute to expanding this agenda beyond the level of individual language families.

Materials and Methods

Data.

The ASJP database (13) is a collection of basic vocabulary lists for 6,895 doculects (i.e., languages and dialects). Each list contains translations of 40 core concepts, such as “I,” “one,” “two,” “person,” “eye,” “nose,” “star,” and “name,” for example. These items were selected (36) as the 40 most stable items from the 100-item Swadesh list (37). All translations are given in a uniform phonetic transcription, using 41 different phonetic symbols (plus diacritics, which were ignored in the present work; the ASJP transcription conventions are given in Table S1).

Table S1.

ASJP transcription conventions

ASJP code symbol	Description	IPA symbols
i	High front vowel, rounded and unrounded	i, i, y, Y
e	Mid-front vowel, rounded and unrounded	e, ø
E	Low front vowel, rounded and unrounded	æ, ε, œ, Œ
3	High and mid-central vowel, rounded and unrounded	ɨ, ɘ, ə, ɜ, ʉ, ɵ, ɞ
a	Low central vowel, unrounded	a, ɐ
u	High back vowel, rounded and unrounded	ɯ, u
o	Mid- and low back vowel, rounded and unrounded	ɣ, ʌ, ɑ, o, ɔ, ɒ
p	Voiceless bilabial stop and fricative	p, ɸ
b	Voiced bilabial stop and fricative	b, β
f	Voiceless labiodental fricative	f
v	Voiced labiodental fricative	v
m	Bilabial nasal	m
w	voiced bilabial-velar approximant	w
8	Voiceless and voiced dental fricative	θ, ð
4	Dental nasal	$\underset{\mathrm{\sqcap }}{{\displaystyle \text{n}}}$
t	Voiceless alveolar stop	t
d	Voiced alveolar stop	d
s	Voiceless alveolar fricative	s
z	Voiced alveolar fricative	z
c	Voiceless and voiced alveolar affricate	ts, X
n	Alveolar nasal	n
r	Voiced apicoalveolar flap and all other varieties of “r-sounds”	ɾ, r, R, ɽ
l	Voiced alveolar lateral approximant	l
S	Voiceless postalveolar fricative	ʃ
Z	Voiced postalveolar fricative	ʒ
C	Voiceless palatoalveolar affricate	ʧ
j	Voiced palatoalveolar affricate	X
T	Voiceless and voiced palatal stop	C, ɟ
5	Palatal nasal	ɲ
y	Palatal approximant	j
k	Voiceless velar stop	k
g	Voiced velar stop	g
x	Voiceless and voiced velar fricative	x, ɣ
N	Velar nasal	ŋ
q	Voiceless uvular stop	q
G	Voiced uvular stop	g
X	Voiceless and voiced uvular fricative, voiceless and voiced pharyngeal fricative	χ, ʁ, ħ, ʕ
h	Voiceless and voiced glottal fricative	h, ɦ
7	Voiceless glottal stop	ʔ
L	All other laterals	l, ɭ, λ
!	All varieties of “click-sounds”	!, |, ||, ǂ

ASJP transcription conventions. Reproduced from ref. 45.

From these data, all doculects were used that (i) are or were spoken in Eurasia or neighboring islands, excluding Eskimo-Aleut and Afro-Asiatic languages; (ii) contain not more than 12 missing entries in their ASJP word list; (iii) did not become extinct before the year 1700; and (iv) are neither pidgins nor creoles. The geographic distribution of these 1,161 doculects is shown in Fig. 3, together with its classification according to Fig. 1. The 58 doculects excluded in the second analysis are shown in gray. [The lists of doculects used can be seen in Dataset S1 (full list of doculects) and Dataset S2/Dataset S3 (reduced list of doculects)].

Fig. 3.

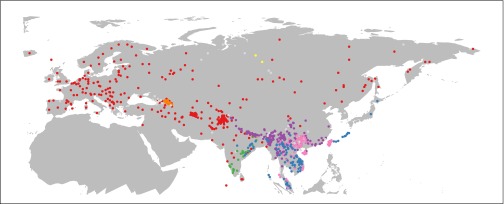
Geographic distribution of the doculects used. Colors refer to the top-level taxa in Fig. 1, and doculects omitted from analysis are shown in light gray.

Rogue Taxa.

For each doculect $L_1$, a data matrix was set up with the doculects $\ne L_1$ as rows and ASJP concepts as columns. The entry for doculect $L_2$/concept c is the calibrated string similarity between $L_1$’s and $L_2$’s entry for c. Cronbach’s alpha was computed column-wise for this matrix. All doculects with alpha values $\text{<}0.6$ were discarded. The same procedure was repeated with the reduced set of doculects until all alpha values remained $\text{≥}0.6$ relative to the reduced set of doculects. In total, 58 doculects were excluded this way (the list is provided in SI Rogue Taxa).

Phylogenetic Techniques.

Phylogenetic inference proceeded in four steps. First, the similarity between individual word forms was determined via weighted sequence alignment. Second, the word similarities between all translation pairs from two word lists were aggregated to a dissimilarity measure between these word lists. Third, a phylogenetic tree was estimated from these pairwise dissimilarities. Finally, confidence values for the branches of that tree were estimated. [The first two steps are described in detail by Jäger (14).]

String similarity via weighted sequence alignment.

Drawing on much prior work in computational linguistics, such as work by Kondrak (38) [an overview over different approaches is provided by Kessler (39)], string similarities are determined via sequence alignment, using differential weights for different symbol pairings. Unlike most previous work in this area, these weights are determined in a data-oriented way via unsupervised learning from the ASJP data.

The basis of this technique is the notion of point-wise mutual information (PMI) (40) [also known as log-odds scores in bioinformatics (cf. 41)] between individual segments. The PMI score of two sound classes a, b is defined as

$$\text{PMI}\left(a,b\right)\doteq \text{log}\frac{\text{likelihood}\hspace{0.17em}\text{that}\hspace{0.17em}a\hspace{0.17em}\text{and}\hspace{0.17em}b\hspace{0.17em}\text{participate}\hspace{0.17em}\text{in}\hspace{0.17em}\text{a}\hspace{0.17em}\text{sound}\hspace{0.17em}\text{correspondence}}{\text{likelihood}\hspace{0.17em}\text{of}\hspace{0.17em}a\times \text{likelihood}\hspace{0.17em}\text{of}\hspace{0.17em}b}.$$

Sound pairs with a positive PMI score provide evidence for relatedness, and vice versa.

To estimate the likelihood of sound correspondences, a corpus of probable cognate pairs was compiled from the ASJP data using two heuristics. First, a crude similarity measure between word lists was defined and the 1% of all ASJP doculect pairs with highest similarity was kept as probably related. (This notion is rather strict; English, for instance, turns out to be “probably related” to all and only the other Germanic doculects. In total, 99.9% of all doculect pairs defined that way belong to the same language family.) Second, the normalized Levenshtein distance (i.e., a somewhat crude distance measure between phonetic strings only counting matches and mismatches) was computed for all translation pairs from probably related doculects. Translation pairs with a distance below a certain threshold were considered as probably cognate. (The technical term “cognate” is not entirely appropriate here because the method also captures word pairs related via borrowing; “etymologically related” might be a more appropriate, if cumbersome, term.) These probable cognate pairs were used to estimate PMI scores. Subsequently, all translation pairs were aligned via the Needleman–Wunsch algorithm (42) using the PMI scores from the previous step as weights. This alignment resulted in a measure of string similarity, and all pairs above a certain similarity threshold were treated as probable cognates in the next step. This procedure was repeated 10 times. In the last step, ∼1.3 million probable cognate pairs were used to estimate the final PMI scores.

Again, the similarity threshold used is rather strict. To illustrate, the only probable cognate pairs between English and German that were kept during the last iteration are fiS/fiS “fish,” laus/laus “louse,” bl3d/blut “blood,” horn/horn “horn,” brest/brust “breast,” liv3r/leb3r “liver,” star/StErn “star,” wat3r/vas3r “water,” and ful/fol “full.”

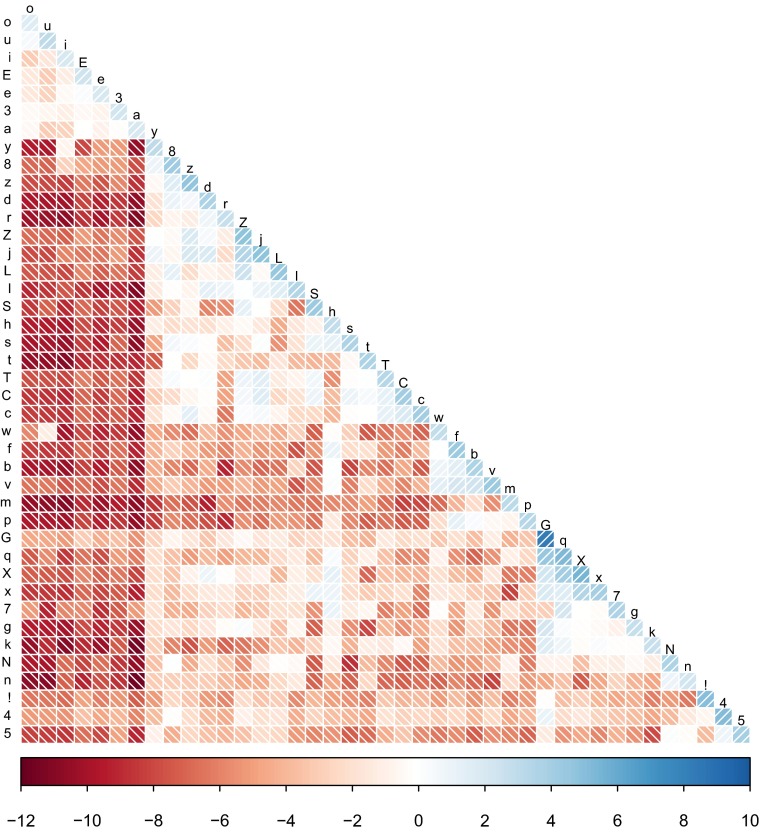
The PMI scores thus obtained are visualized in Fig. 4 (numerical values are given in Dataset S4). It is easy to discern that matches between identical sounds always result in a positive score, but there are differences. An identity match between two vowels, for instance, carries less weight than a self-match for a rare consonant class, such as dental fricatives (8 in the ASJP transcription).

Fig. 4.

PMI between ASJP sound classes.

Mismatches between different sound classes mostly result in negative values, but there is considerable differentiation. Mismatches between a vowel and a consonant generally have very negative scores, except for the pairings u/w and i/y (which both involve semivowels). The score for matching two different vowels or two different consonants with an identical place of articulation has a score close to 0. Some such pairings even have positive scores (e.g., o/u, d/8), indicating that such a pairing constitutes positive evidence for etymological relatedness. In a small number of cases, pairings with a different place of articulation have a positive score (e.g., h paired with other fricatives, such as f, s, or x).

These PMI scores arguably capture linguistic intuitions about how informative possible sound correspondences are for establishing etymological relations. They do not capture regular sound correspondences between specific languages, however. Although it is ultimately desirable to incorporate those sound correspondences into a quantitative model of string similarity [recent approaches using much richer data over smaller collections of languages are discussed elsewhere (33, 34)], the amount of data available at the scale considered here does not afford reliable model fitting for such complex models.

The aggregate PMI score of a pair of aligned strings (where gaps may be inserted at any position) is defined as the sum of the PMI scores of the aligned symbol pairs. Matching a symbol with a gap incurs a penalty, with different penalties for initial and noninitial positions in a sequence of consecutive gaps (so-called “affine gap penalties”). The values of the gap penalties were obtained via an optimization technique (cf. 14). The similarity $s\left(w_1,w_2\right)$ between two strings $w_1,w_2$ is then defined as the minimal aggregate PMI score for all possible alignments. It can be computed efficiently with the Needleman–Wunsch algorithm.

To illustrate this notion, consider the word pairs hant/hEnt (German and English for “hand”) vs. hant/mano (German and Spanish for “hand”). In both cases, we find two matches and two mismatches in the optimal alignment. However, the mismatches in the first pair (a/E, t/d) carry little weight, resulting in an overall highly positive score of 4.80. In the second pair, the mismatches (h/m, t/o) carry large weight; the overall PMI score is $-11.28$.

It depends on the pair of languages being compared as to how informative a certain word similarity level is as a predictor for cognacy. For instance, the Polish word list contains seven sound classes not occurring in the English word list, whereas the Dutch word list only contains three such sound classes. Consequently, the probability of chance matches is higher when comparing English with Dutch as opposed to the English/Polish comparison. The average similarity between nonsynonymous word pairs (i.e., likely noncognates) for English/Dutch is $-6.54$, whereas this value is $-8.53$ for English/Polish. Hence, the bar for establishing cognacy between English and Dutch is higher than for English/Polish.

The calibrated similarity $s_c\left(w_1,w_2|L_1,L_2\right)$ between two synonymous words $w_1,w_2$ from two languages $L_1,L_2$ is derived from the probability that the degree of similarity between $w_1$ and $w_2$ could be due to chance, given $L_1$ and $L_2$. Formally, it is defined as

$$s_c\left(w_1,w_2|L_1,L_2\right)=\begin{array}{c}-\text{log}\frac{1+\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{non}-\text{synonymous}\hspace{0.17em}\text{pairs}\hspace{0.17em}\left(w\in L_1,w\prime \in L_2\right)\hspace{0.17em}\text{with}\hspace{0.17em}s\left(w,w\prime \right)>s\left(w_1,w_2\right)}{1+\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{non}-\text{synonymous}\hspace{0.17em}\text{pairs}\hspace{0.17em}\left(w\in L_1,w\prime \in L_2\right)}\end{array}.$$

It measures the similarity between $w_1$ and $w_2$ relative to the general distribution of string similarities between words from $L_1$ and $L_2$.

Dissimilarities between word lists.

The dissimilarity or distance between the two-word list $L_1,L_2$ is inversely related to the mean calibrated similarity ${\widehat{s}}_c\left(L_1,L_2\right)$:

$$d\left(L_1,L_2\right)\doteq \log s_c^{\text{max}}-\text{log}{\widehat{s}}_c\left(L_1,L_2\right),$$

where $s_c^{\text{max}}$ is the maximal value a calibrated string similarity can assume; for word lists of length n, this value is $\log \left(1+n\left(n-1\right)\right)$. The matrix of pairwise dissimilarities for all ASJP doculects can be inspected online at www.evolaemp.uni-tuebingen.de/details.html.

Phylogeny induction.

Note that the approach pursued here does not involve binary decisions in favor or against cognacy of a word pair. Rather, calibrated similarity captures the degree of likelihood that a pair is cognate. Therefore, the character-based models of phylogenetic inference that have become standard in phylogenetic linguistics (6, 7) are not applicable. Also, character-based inference over 1,000 taxa would touch the limits of currently available computing power. Distance-based phylogenetic inference offers a viable alternative.

Using the method described above, a dissimilarity matrix between all word lists under investigation is computed. This matrix is used as input for phylogenetic inference utilizing the greedy minimum evolution algorithm, followed by optimization utilizing generalized nearest neighbor interchange (15). The location of the root of the tree was determined using the method from Steel and McKenzie (43), utilizing a maximum-likelihood estimation under the assumption that the tree topology is generated by a Yule process.

The phylogenetic trees for the full and reduced datasets (annotated with confidence values), plus the tree where all branches with confidence $<0.95$ are collapsed, are given in Datasets S1–S3.

Bayesian bootstrap confidence values.

Branch confidence values were determined using a Bayesian version of the bootstrap interior branch test (17).

Using a variant of Bayesian bootstrap (44), 1,000 probability vectors over the similarity matrices for the 40 ASJP concepts were sampled according to a Dirichlet distribution with all parameters $=2$. (This choice corresponds to a posterior distribution upon observing each concept once, based on a uniform prior.) For each bootstrap probability vector $\overrightarrow{p}$, a distance matrix d over doculects was computed according to the formula

$$d_{i,j}=\log s_c^{\text{max}}-\text{log}\langle \overrightarrow{p},{\overrightarrow{s}}_c\left(i,j\right)\rangle ,$$

where ${\overrightarrow{s}}_c\left(i,j\right)$ is the vector of calibrated string similarities between doculects $L_i$ and $L_j$.

In the next step, the optimal branch lengths, minimizing the mean squared error, of the tree topology $\mathcal{T}$ defined above was computed for each bootstrapped distance matrix d. The confidence value for an interior branch b was defined as the proportion of bootstrap samples for which b’s optimal length is $>0$.

SI Rogue Taxa

The following doculects were excluded from the analysis (doculect names as they appear in the ASJP database): ABAZA, ABKHAZ, ADYGHE, ALBANIAN_GHEG, ARIN, BASQUE, BRAHUI, BUGAN, BUGAN_2, BUGUN, BUNU, BURUSHASKI, DEURI, DHIMAL, GAELIC_SCOTTISH, GEORGIAN, GREEK, GUNDONG_PA_HNG, HONGFENG_GELAO, JIARONG_2, KABARDIAN, KARAGASSISCH, KHANTY, KOREAN, KOTT, KUSUNDA, LAK, LAZ, MANSI, MANX, MINGRELIAN, MULAO_KADAI, NA_KHE_GELAO, NAGA_MAO, NAGA_POCHURI, NAGA_SUMI, NAHALI, NENETS, NIHALI, NORTHERN_TUJIA, NUMAO_BUNU, PA-HNG, PALIU, PHUNOI, PUTIAN_CHINESE, QIANG_LONGXI, SELKUP, SHERDU.K.PEN, SHIMENKAN_HMONG, SHOM_PENG. SULUNG, SVAN, TARAON, UBYKH, UDI, YERONG, YU.K.AGHIR_TUNDRA, ZHABA.