A new way of quantifying diagnostic information from multilead electrocardiogram for cardiac disease classification

Abstract

A new measure for quantifying diagnostic information from a multilead electrocardiogram (MECG) is proposed. This diagnostic measure is based on principal component (PC) multivariate multiscale sample entropy (PMMSE). The PC analysis is used to reduce the dimension of the MECG data matrix. The multivariate multiscale sample entropy is evaluated over the PC matrix. The PMMSE values along each scale are used as a diagnostic feature vector. The performance of the proposed measure is evaluated using a least square support vector machine classifier for detection and classification of normal (healthy control) and different cardiovascular diseases such as cardiomyopathy, cardiac dysrhythmia, hypertrophy and myocardial infarction. The results show that the cardiac diseases are successfully detected and classified with an average accuracy of 90.34%. Comparison with some of the recently published methods shows improved performance of the proposed measure of cardiac disease classification.

1. Introduction

Cardiac ailments are among the major causes of death in the world, as per the World Health Organization's estimation [1]. Multilead electrocardiogram (MECG) is used as a standard tool for the diagnosis of cardiovascular diseases. Different types of diseases such as bundle branch block, cardiomyopathy (CM), hypertrophy (HT), cardiac dysrhythmia (DT), myocardial infarction (MI) and valvular disease [2] are diagnosed by MECGs. Digital signal processing plays an important role in quantifying the diagnostic information from an electrocardiogram (ECG) signal. There are a number of methods reported in the literature for measuring diagnostic information from ECG signals [3–6]. These methods use a single lead ECG. However, cardiologists use MECGs for accurate assessment and localisation of pathologies [2]. For computer aided diagnosis, it is beneficial to use MECGs for estimation of diagnostic information.

In this Letter, we propose a new measure for quantifying diagnostic information from MECGs. This measure is aimed at detection and classification of normal (healthy control, HC) and cardiac ailments such as CM, HT, DT and MI. The proposed measure is based on the principal component (PC) multivariate multiscale sample entropy (PMMSE). The MECG data are subjected to PC analysis (PCA). In the PCA domain, the first few PCs capture the significant clinical components of the MECG. The multivariate multiscale sample entropy (MMSE) is evaluated over the reduced PC matrix. The performance of PMMSE features is evaluated using least square support vector machine (LS-SVM) classifier. The rest of this Letter is organised as follows. In Section 2, the proposed PMMSE diagnostic measure is described. The results and discussions are presented in Section 3 and in Section 4, conclusions are drawn.

2. Method

Fig. 1 depicts a block diagram of the proposed method. The block diagram comprises of three stages. These are pre-processing and frame-based segmentation, PMMSE evaluation and classification using LS-SVM. A detailed description of each of the stages is given in the following subsections.

Figure 1.

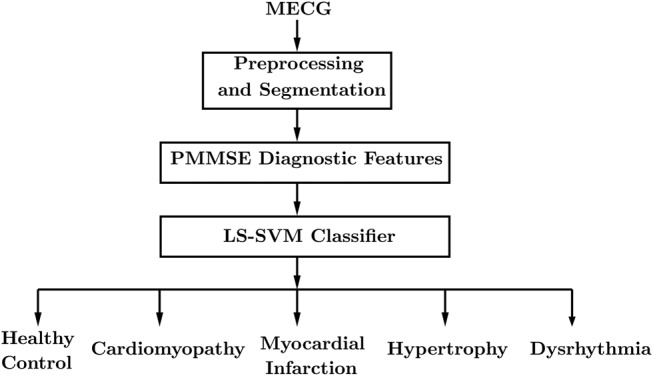
Block diagram for classification of cardiac ailments from MECG

2.1. Pre-processing

An MECG contains different types of noises [7]. First, these noises are filtered out [8]. Then, the Pan and Tompkin algorithm is used for detection of the QRS-complexes [9]. After the R-point detection, the MECG signals are divided into frames of 4 s duration each, which correspond to approximately four beats. MECGs have three types of correlations. These are inter-lead, intra-beat and intra-sample correlations [10]. The inter-lead correlation corresponds to the correlation between leads in the MECG. The inter-sample correlation corresponds to the correlation between samples along each lead. Similarly, the intra-beat correlation is the correlation between the rhythms or RR-intervals. The beat-by-beat segmentation of the MECG can reveal the inter-sample and the inter-lead correlations. The DT (sinus arrhythmia, premature ventricular ectopic beats, supra ventricular arrhythmia and ventricular arrhythmia), HT (supra-ventricular and ventricular HT), bundle branch block and acute myocardial ischaemia pathologies are diagnosed from intra-beat or RR-interval variations in ECGs [11, 12]. To exploit intra-beat correlation, frame-based processing is needed.

2.2. Proposed PMMSE diagnostic measure

PCA is an unsupervised learning method used in filtering [13], compression [8], feature extraction [14] and dimension reduction [15]. The PCA of MECG is defined by B = XV. The atoms (columns) of matrix B are the PCs and X is the MECG data matrix. The size of the MECG data matrix is n × m, where n and m are the number of samples and number of channels, respectively. The eigen matrix V transforms the MECG data matrix into PC domain. The first six PCs contain significant diagnostic information [8]. The MMSE has recently been proposed to measure the regularity in multichannel time-series data [16]. In this work, the MMSE is evaluated over the reduced PC matrix (B). The algorithm for evaluation of PMMSE is given below:

• The reduced PC matrix B is obtained by applying PCA of MECG data. The matrix B is defined by $[(b_{q,k}{)}_{k=1}^n]$, where q = 1, 2, ..., 6 represents the number of PCs and n is the length of each PC.

• A coarse grained PC multivariate data matrix ${\mathit{Y}}_j^{ϵ}=y_{q,j}^{ϵ}$ is evaluated from $b_{q,k}^{ϵ}$. The $y_{q,j}^{ϵ}$ is defined by

  $$y_{q,j}^{ϵ}=\frac{{\sum }_{k=(j-1)ϵ+1}^{jϵ}{b}_{q,k}}{ϵ}$$ (1)

  where $1\le j\le (n/ϵ)$, ε represents the scales (label of decomposition).

• The PMMSE is defined as the multivariate sample entropy of the coarse grained PC multivariate data matrix ${\mathit{Y}}_j^{ϵ}$ at a scale of ε. The number of scales (decomposition labels) varies from ε = 1 to ε = 20.

The multivariate sample entropy is evaluated using composite delay, embedding and time-lag vectors [16]. The composite delay vector for q variate time-series data $[(y_{q,j}{)}_{j=1}^n]$ is given by

$$\begin{array}{rl}{\mathit{y}}_m(j)& =[y_{(1,j)},y_{(1,j+\tau )},\dots ,y_{(1,j+(m_1-1)\tau )}\\ & y_{(2,j)},y_{(2,j+\tau )},\dots ,y_{(2,j+(m_2-1)\tau )}\\ & y_{(q,j)},y_{(q,j+\tau )},\dots ,y_{(q,j+(m_q-1)\tau )}]\end{array}$$ (2)

The embedding and time lag vectors are given by m = [m₁, m₂, ..., m_q] and τ = [τ₁, τ₂, ..., τ_q]. The composite delay vector y_m(j) ∈ R^m contains ‘m’ elements with $m={\sum }_{j=1}^q{m}_j$. The multivariate sample entropy is evaluated in five steps as

1. the (n–p) number of composite delay vectors are computed. Each composite delay vector is in the form of y_m(j) ∈ R^m with (j = 1, 2,..., n − p). The value of ‘p’ is given by p = max(m) × max(τ);

2. the distance between the jth and the kth composite vectors is given as

   $$\mathit{D}[{\mathit{y}}_m(j),{\mathit{y}}_m(k)]=max{}_{l=1,2,...,m}\left|x(j+l-1)-x(k+l-1)\right|$$ (3)

3. then, the total number of distances for the jth composite delay vector is evaluated with respect to a certain condition. This condition is given as D[y_m(j), y_m(k)] ≤ r, j ≠ k. where r is a threshold value. The total number of distances for the jth composite delay vector is denoted as d_j;

4. the frequency of occurrence is given as ${\mathit{B}}_j^m(r)=(1/(n-p-1)){\mathit{d}}_j$. Then, the B^m(r) value is given as ${\mathit{B}}^m(r)=(1/q(n-p)){\sum }_{i=1}^{q(n-p)}{\mathit{B}}_j^m(r)$;

5. similarly, the B^m+1(r) is evaluated by extending the dimension of composite delay vector to (m + 1). Then, the multivariate sample entropy is given by

   $$e(m,\tau ,r,n)=-\ln \left[\frac{{\mathit{B}}^{m+1}(r)}{{\mathit{B}}^m(r)}\right]$$ (4)

2.3. Classification using LS-SVM

The 20-dimensional PMMSE-based feature vector from normal as well as pathological MECG frames is used as an input to multiclass LS-SVM classifier. The LS-SVM classifier detects and classifies different cardiac ailments. In this work, the HC, HT, MI, DT and CM are five different classes. LS-SVM is based on the least square conceptualisation of the support vector machine (SVM) [17]. It is widely used in applications such as function estimation [18] and electroencephalography time-series classification [19]. In this work, the LS-SVM with polynomial (poly) and radial basis function (RBF) kernels is used. For selecting training and testing instances, the 5-fold-based cross-validation technique is used [5]. Fig. 2 depicts the selection of training and testing instances of each class. In each fold, 4/5th of the instances are used for training. For testing, the remaining 1/5th are used. The accuracy values along each fold are evaluated. The total accuracy of the LS-SVM classifier is the average of accuracy value along each fold.

Figure 2.

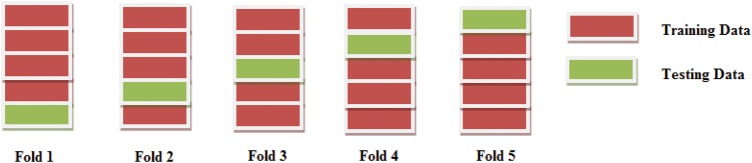
Selection of training and testing instances from each class using 5-fold cross-validation scheme

3. Result and discussion

For testing of the proposed method, a publicly available database (PTB diagnostic ECG database) is used [20]. This database comprises of both normal and pathological MECG signals with 15 leads, 1000 Hz sampling frequency and 16 bit resolution. In this work, we have used 16, 15, 11, 7 and 16 pathological MECG signals such as MI, CM, DT, HT and HC. The lead I, II, III, aVR, aVL, aVF, V1, V2, V3, V4, V5 and V6 ECG signals are used. The MECG signals are subjected to pre-processing and frame-based segmentation. After segmentation, PCA is applied to each MECG frame. The signals for the different PCs of CM, DT, MI and HT pathological and HC MECGs are shown in Fig. 3. It is observed that the signal characteristics from the same PC are different for the pathologies and HC. The variations in signal characteristics along each PC, depending on the pathology, are highlighted and shown in Figs. 3a–e. The signals vary across the different PCs for the same pathology. These characteristics can be used for detection and classification of pathologies.

Figure 3.

PCs PC1, PC2, PC3, PC4, PC5, PC6 for HC, CM, HT, MI and DT MECG frames

Fig. 4 depicts the probability density plot of the first ten PMMSE features for normal and pathological MECG frames. It is evident that the peaks in the probability density plot are different for pathological and normal cases. The mean and standard deviation values for the first ten PMMSE features are shown in Table 1. It is observed that the mean and standard deviation of PMMSE features are highest for the CM pathology-based MECG frames. Due to CM pathology, the heart muscle enlarges and, as a result, pumping of blood in the heart decreases [2]. The irregular heartbeats generated in ECGs are due to the consequential CM. As the PMMSE captures the irregularity along each of the PCs, the PMMSE value along each scale shows a higher standard deviation value than that of HC and other pathologies. The standard deviation of PMMSE features in the case of HT is less than in other pathologies. The PMMSE features for the HC class have the lowest mean value compared to those of the MI, CM, HT and DT classes. From these results it can be concluded that the PMMSE features extracted from the PCs will capture the diagnostic information that can differentiate between cardiac diseases.

Figure 4.

Probability density plots of first ten PMMSE features for CM, HT, MI, DT and HC subjects

Table 1.

Mean and standard deviation values of first ten PMMSE features

Classes	Parameters	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10
HC	μ	0.2551	0.2497	0.2464	0.2445	0.2435	0.2434	0.2429	0.2424	0.2426	0.2429
HC	σ	0.0750	0.0754	0.0758	0.0763	0.0765	0.0768	0.0773	0.0775	0.0780	0.0789
CM	μ	0.3360	0.3329	0.3309	0.3293	0.3281	0.3273	0.3268	0.3260	0.3257	0.3257
CM	σ	0.1278	0.1284	0.1281	0.1272	0.1255	0.1242	0.1232	0.1216	0.1211	0.1204
MI	μ	0.3351	0.3294	0.3253	0.3228	0.3217	0.3208	0.3199	0.3185	0.3181	0.3173
MI	σ	0.0908	0.0930	0.0948	0.0958	0.0966	0.0969	0.0984	0.0990	0.0995	0.1006
DT	μ	0.2808	0.2765	0.2739	0.2723	0.2715	0.2710	0.2708	0.2706	0.2704	0.2710
DT	σ	0.0890	0.0901	0.0911	0.0921	0.0932	0.0945	0.0960	0.0971	0.0983	0.1005
HT	μ	0.2937	0.2889	0.2861	0.2845	0.2837	0.2834	0.2833	0.2838	0.2835	0.2842
HT	σ	0.0629	0.0634	0.0638	0.0645	0.0652	0.0660	0.0666	0.0681	0.0682	0.0683

In this work, 63 HT, 144 MI, 135 CM, 99 DT and 140 HC MECG frames are extracted. The PMMSE features from each MECG frame are computed. The performance of PMMSE diagnostic features are evaluated using a multiclass LS-SVM classifier. Two different multiclass coding techniques are used. These are ‘One VS One’ and ‘One VS All’. The training and testing instances or frames are chosen on the basis of 5-fold cross-validation. Table 2 shows individual class accuracy values of LS-SVM classifier with polynomial kernel and ‘One VS One’ multiclass coding technique. For the MI class, detection accuracy values are 88.88, 93.05, 90.27, 88.88 and 88.88% in Fold1, Fold2, Fold3, Fold4 and Fold5, respectively. Similarly, for the HC class, accuracy values are 83.75, 88.12, 86.25, 89.37 and 90.62%. The detection accuracy for the HT class is lower than for other pathological cases along each fold. The individual class accuracy values of LS-SVM classifier with RBF kernel and ‘One VS One’ multiclass coding method is shown in Table 3. It has been observed that accuracy values for LS-SVM classifier with RBF kernel are higher than those of polynomial kernel-based LS-SVM, for the ‘One VS One’ multiclass coding technique.

Table 2.

Individual class accuracy values for LS-SVM classifier with polynomial kernel and ‘One VS One’ multiclass coding technique

Classes	Fold1, %	Fold2, %	Fold3, %	Fold4, %	Fold5, %
HC	83.75	88.12	86.25	89.37	90.62
CM	75.55	85.18	86.66	85.18	78.51
MI	88.88	93.05	90.27	88.88	88.88
DT	82.82	76.77	78.80	70.70	73.71
HT	65.07	85.71	79.36	57.14	68.25

Table 3.

Individual class accuracy values for LS-SVM classifier with RBF kernel and ‘One VS One’ multiclass coding technique

Classes	Fold1, %	Fold2, %	Fold3, %	Fold4, %	Fold5, %
HC	87.87	86.25	81.87	85.62	89.37
CM	58.51	78.51	73.33	76.29	82.22
MI	88.19	88.88	82.63	84.72	84.72
DT	86.86	86.86	85.84	81.80	85.84
HT	69.84	84.12	90.47	85.71	88.88

The individual class accuracy values of polynomial and RBF kernel-based LS-SVM classifier with the ‘One VS All’ multiclass coding method are shown in Tables 4 and 5. It is seen that both polynomial and RBF kernel LS-SVM with ‘One VS All’ multiclass coding scheme have higher accuracy values than in previous cases. The accuracy values of LS-SVM classifier with polynomial and RBF kernel and different multiclass coding methods are shown in Table 6. It is observed that the RBF kernel LS-SVM with ‘One VS All’ multiclass coding technique has higher accuracy values of 91.28, 90.26, 89.83, 90.48 and 89.87% along Fold1, Fold2, Fold3 and Fold4; the polynomial kernel LS-SVM has higher accuracy at Fold5 than that of RBF kernel LS-SVM. The average accuracy of RBF kernel LS-SVM classifier with ‘One VS All’ multiclass coding approach is found to be 90.34%. This value is higher than RBF as well as polynomial kernel LS-SVM with ‘One VS One’ multiclass coding scheme. It can be concluded that the ‘One VS All’ multiclass coding approach-based LS-SVM detects and classifies the cardiac diseases effectively from the PMMSE features.

Table 4.

Individual class accuracy values for LS-SVM classifier with polynomial kernel and ‘One VS All’ multiclass coding technique

Classes	Fold1, %	Fold2, %	Fold3, %	Fold4, %	Fold5, %
HC	88.12	92.5	85.00	93.75	82.5
CM	91.85	90.37	96.29	90.37	94.81
MI	94.67	93.75	93.75	91.66	94.67
DT	90.90	87.87	89.89	90.90	90.90
HT	87.30	84.12	82.53	82.53	88.88

Table 5.

Individual class accuracy values for LS-SVM classifier with RBF kernel and ‘One VS All’ multiclass coding technique

Classes	Fold1, %	Fold2, %	Fold3, %	Fold4, %	Fold5, %
HC	88.58	92.82	85.53	93.85	86.19
CM	92.31	91.58	95.38	91.17	94.72
MI	95.83	94.20	94.20	92.25	93.28
DT	91.25	88.17	90.90	90.53	89.61
HT	88.47	84.64	83.15	84.64	85.57

Table 6.

Accuracy values for LS-SVM classifiers along each fold

Classifiers	Coding scheme	Fold1, %	Fold2, %	Fold3, %	Fold4, %	Fold5, %
LSSVM-Poly	One VS One	79.21	85.76	84.26	78.25	80.00
LSSVM-RBF	One VS One	78.25	84.92	82.82	82.82	86.20
LSSVM-Poly	One VS All	89.80	89.72	89.49	89.84	90.18
LSSVM-RBF	One VS All	91.28	90.26	89.83	90.48	89.87

The performance of the proposed PMMSE measure is compared with vector cardiography-based disease detection methods.

Dehnavi et al. [21] proposed a method for the detection and classification of myocardial ischaemia using the neural network. They have used independent component analysis and PCA to extract features from vectorcardiogram (VCG) signals. An accuracy of 73% is found using the neural network. Eriksson et al. [22] proposed a method for the detection and classification of acute MI and bundle branch block. They have used QRS-complex and ST-segment shape magnitudes as features. A detection accuracy of 71 and 77% has been found for bundle branch block and MI cardiac ailments, respectively. Multiscale recurrence quantification analysis from VCG signals has been proposed [23] for classification of MI and HC subjects. Discrete wavelet transform is used to segregate the clinical components of VCG into different scales. The recurrence quantification analysis is performed over each sub-band to extract various features. The quadratic discriminant analysis, linear discriminant analysis and K-nearest neighbour classifiers are used for detection of MI. Individual class detection accuracy (sensitivity and specificity) values of 75 and 96.5% have been found for HC and MI classes, respectively. The performance of the proposed PMMSE measure with LS-SVM classifier has the highest accuracy value of 89.39, 93.03, 93.95, 90.09 and 85.29% for HC, CM, MI, DT and HT, respectively. This shows that the proposed PMMSE measure with LS-SVM classifier has a better performance than other methods.

4. Conclusion

In this Letter, a new measure for quantifying diagnostic information from MECG is proposed. The measure is defined as the principal component multivariate multiscale sample entropy (PMMSE). PMMSE values along different scales are used as the diagnostic feature vector for the detection and classification of different cardiovascular diseases such as CM, CT, MI and HT. An average accuracy of 90.34% is found using the LS-SVM classifier with RBF kernel function and ‘One VS All’ multiclass coding technique. Comparison with existing methods shows that the proposed PMMSE measure with LS-SVM classifier has a better performance.