Comparative study of ECG signal denoising by wavelet thresholding in empirical and variational mode decomposition domains

Abstract

Hybrid denoising models based on combining empirical mode decomposition (EMD) and discrete wavelet transform (DWT) were found to be effective in removing additive Gaussian noise from electrocardiogram (ECG) signals. Recently, variational mode decomposition (VMD) has been proposed as a multiresolution technique that overcomes some of the limits of the EMD. Two ECG denoising approaches are compared. The first is based on denoising in the EMD domain by DWT thresholding, whereas the second is based on noise reduction in the VMD domain by DWT thresholding. Using signal-to-noise ratio and mean of squared errors as performance measures, simulation results show that the VMD-DWT approach outperforms the conventional EMD–DWT. In addition, a non-local means approach used as a reference technique provides better results than the VMD-DWT approach.

1. Introduction

The electrocardiogram (ECG) signal is widely used to measure and to diagnose cardiac activity and arrhythmia in clinical environments. Thus, it is an important tool for the diagnosis of cardiac abnormalities to monitor urgent treatments. However, ECG signal can be corrupted by unwanted interference such as power line interference, electrode contact noise, motion artefacts, muscle contraction, baseline drift, ECG signal amplitude modulation with respiration, instrumentation noise and electrosurgical noise [1].

Several approaches have been proposed in the literature to denoise ECG signal with the purpose of obtaining a denoised ECG that facilitates easy and accurate interpretation. The proposed approaches include filter banks [2], independent component analysis [3, 4], adaptive filtering [5, 6], discrete wavelet transform (DWT) [7–9] and empirical mode decomposition (EMD) [10–13]. When compared with other approaches, the denoising methods based on EMD and wavelet are found to be more effective in reducing noise from the ECG signals [12]. Indeed, a hybrid EMD–DWT approach has been proposed in the literature [11, 12, 14] to achieve accurate denoising performance for the ECG signal. For instance, the DWT is a suitable tool for isolating transient (non-stationary) changes in a time series by combining the time-domain and frequency-domain analysis [15]. In addition, the advantage of the DWT is that the windows vary, and it has an infinite set of possible basis functions [13]. Particularly, the basic wavelet transform starts with a basis function, the mother wavelet, and decomposes a signal into components of different time and frequency scales; longer time intervals are used to obtain low-frequency information and shorter intervals are used to obtain high-frequency information. Besides, the EMD [16] is an adaptive and data-driven technique used for processing non-linear and non-stationary signals in addition to stationary signals. The EMD decomposes a given signal into a finite sum of components plus a residue. The components are called intrinsic mode functions (IMF) and are local and auto-adaptive. Low order IMF represent fast oscillation or high-frequency modes, and high order IMF represent slow oscillation (low-frequency) modes. As a result, the EMD is well suited for biomedical signal analysis [13]. Owing to the effectiveness of the hybrid EMD–DWT model, it was also successfully applied to other signal processing problems including denoising of electrostatic signals [17], ultrasonic images [18] and hyperspectral images [19].

However, the EMD algorithm suffers from a lack of exact mathematical model, interpolation choice, and sensitivity to both noise and sampling [20]. Very recently, as an alternative to the EMD algorithm, Dragomiretskiy and Zosso [20] proposed an entirely non-recursive variational mode decomposition (VMD) model, where the modes are extracted concurrently. In particular, the VMD model searches for a number of modes and their respective centre frequencies, such that the band-limited modes reproduce the input signal exactly or in least-squares sense [20]. Using simulated harmonic functions, Dragomiretskiy and Zosso [20] found that the VMD as a denoising approach outperforms the EMD.

This Letter is therefore aimed to compare two hybrid systems for the purpose of ECG denoising; namely the conventional EMD–DWT and the VMD-DWT model. Indeed, we investigate whether the VMD can outperform the EMD in denoising the ECG signal. In addition, we also evaluate the performance of these methods against the non-local means (NLM) approach [21], which was recently found to be effective in denoising ECG signals.

In this Letter, three approaches are investigated in denoising the original ECG signal, which is corrupted with additive Gaussian noise. In the first approach, the EMD is applied to the noisy ECG signal for decomposition purposes to obtain IMF. Then, the DWT-based thresholding technique is applied to each obtained IMF. Indeed, thresholding the wavelet coefficients is the most straightforward way of distinguishing information from noise in the wavelet domain [22]. In this Letter, the optimal threshold value is determined by minimising Stein's unbiased risk estimator (SURE) [23] called SureShrink and was proposed by Donoho and Johnstone [24]. The SURE was chosen because it is more accurate as more data are available [22]. Finally, the denoisied ECG signal is reconstructed by summing up the denoised IMF. In the second approach, the VMD is applied to the noisy ECG signal for decomposition purpose to obtain variational modes. Similar to the EMD–DWT denoising approach, the DWT-based thresholding technique is applied to each obtained variational mode. Then, the denoised ECG signal is reconstructed by summing up the denoised variational modes. In the third approach; which is also used for comparison purposes; the non-local means approach is applied to the noisy ECG signal to obtain the denoised one. For all the experiments, the well known signal-to-noise ratio (SNR) and mean of squared errors (MSE) are adopted as the main performance measures. In summary, our work contributes to previous works found in the literature [11, 12, 14, 25] by comparing the conventional hybrid EMD–DWT with the new VMD-DWT approach and adopting the NLM technique as a reference model.

The remainder of this Letter is organised as follows; Section 2 presents the methods, Section 3 applies these methods to ECG signals and presents the experimental results, and finally, conclusions are provided in Section 4.

2. Methods

The EMD [16] decomposes a signal into a sum of functions. Each of these functions has the same number of zero crossings and extrema, and is symmetric with respect to its local mean. These functions are called IMF and are found at each scale going from fine to coarse by an iterative procedure called sifting algorithm. Finally, the signal s(t) can be expressed as follows

$$s(t)=\sum _{j=1}^N{\mathrm{IMF}}_j(t)+r_N(t)$$ (1)

where N is the number of IMF, which are nearly orthogonal to each other, and all have nearly zero means; and r_N(t) is the final residue, which is the low-frequency trend of the signal s(t). Usually, the standard deviation (SD) computed from two consecutive sifting results is used as criteria to stop the sifting process by limiting the SD size as follows

$$\mathrm{SD}(k)=\frac{{\sum }_{t=0}^T{\left|d_{k-1}(t)-d_k(t)\right|}^2}{{\sum }_{t=0}^T{d}_{k-1}^2(t)}<\epsilon$$ (2)

where k is the index of the kth difference between the signal s(t) and the envelope mean e(t). The term ε is a pre-determined stopping value.

The purpose of the VMD [20] is to decompose an input signal into k discrete number of sub-signals (modes), where each mode has limited bandwidth in the spectral domain [20]. Thus, each mode k is required to be mostly compact around a centre pulsation ω_k determined along with the decomposition [20]. The VMD algorithm to assess the bandwidth of a one-dimensional signal is as follows [20]: (i) for each mode u_k, compute the associated analytic signal by means of the Hilbert transform to obtain a unilateral frequency spectrum, (ii) for each mode, shift the mode's frequency spectrum to baseband by mixing with an exponential tuned to the respective estimated centre frequency and (iii) estimate the bandwidth through Gaussian smoothness of the demodulated signal, for example, the squared L2-norm of the gradient. Then, the constrained variational problem is given by [20]

$$\begin{array}{c}min\\ u_k,{\omega }_k\end{array}=\left\{\sum _k{∥{\mathrm{\partial }}_t\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast u_k(t)\right]{\mathrm{e}}^{-\mathrm{j}{\omega }_{k}t}∥}_2\right\}$$ (3)

Subject to

$$\sum _k{u}_k=f$$ (4)

where f is the signal, u is its mode, ω is the frequency, δ is the Dirac distribution, t is the time script, k is the number of modes and * denotes convolution. The mode u with high-order k represents the low-frequency components.

In general, wavelet thresholding involves three steps. First, the signal (e.g. the ECG signal) is processed with a DWT [26] for decomposition purposes. As a result, the signal is decomposed into low–low, low–high, high–low and high–high sub-bands. Then, a non-linear thresholding is performed on each DWT sub-band coefficient. In particular, if the DWT coefficient is smaller than the threshold it is set to zero. Otherwise, it is kept or modified. Finally, an inverse DWT is performed to recover the denoised signal. Donoho and Johnstone [24] proposed an approach to determine the optimal threshold value based on the minimisation of SURE denoted by R_s(t), which is given by

$$R_{\mathrm{s}}(t)=N+{∥g(y)∥}^2+2{\mathrm{\nabla }}_y\cdot g(y)$$ (5)

where g is a function in ℜ, y = [y₀, y₁,…, y_{M − 1}] and

$${\mathrm{\nabla }}_y\cdot g(y)=\sum _{i=0}^{N-1}\frac{\mathrm{\partial }{g}_i}{\mathrm{\partial }{y}_i}$$ (6)

Using the standard soft-thresholding function, the selected threshold t_s is given by

$$t_{\mathrm{s}}=\underset{t\in \{y_0,y_1,\dots ,y_{N-1}\}}{\arg min}{R}_{\mathrm{s}}(t)$$ (7)

The NLM denoising approach estimates the denoised signal s_nlm(t) for a given sample s as a sum of values at other points t that are within some search neighbourhood N(s) as follows [21]

$$s_{\mathrm{nlm}}(s)=\frac{1}{z(s)}\sum _{t\in N(s)}w(s,t)v(t)$$ (8)

where z(s) and weights w(s, t) are given by [22, 27]

$$z(s)=\sum _{t}w(s,t)$$ (9)

$$w(s,t)\equiv \exp \left(-\frac{d^2(s,t)}{2L_{\mathrm{\Delta }}{\lambda }^2}\right)$$ (10)

where λ is a bandwidth parameter, Δ is a local patch of samples surrounding s containing L_Δ samples, d² denotes the summed, squared point-by-point difference between samples in the patches centred on s and t [21]. Finally, each patch in (10) is averaged with itself with weight w(s, s) = 1 [21], and a centre patch correction is applied to achieve a smoother result. It is given by [21]

$$w(s,s)=\underset{t\in N(s),t\ne s}{max}w(s,t)$$ (11)

Finally, to evaluate the effectiveness of each ECG signal denoising approach, the SNR, which is expressed in decibel and the MSE are computed. The SNR and MSE are given by

$$\mathrm{SNR}=10{\log }_{10}\left(\frac{{\sum }_{n=1}^N{\left|y\left[n\right]-x\left[n\right]\right|}^2}{{\sum }_{n=1}^N{\left|x_r\left[n\right]-x\left[n\right]\right|}^2}\right)$$ (12)

$$\mathrm{MSE}=\frac{1}{N}\sum _{n=1}^N{\left(x\left[n\right]-x_r\left[n\right]\right)}^2$$ (13)

where x[n] denotes the original ECG signal, y[n] is the noisy ECG signal, x_r[n] is the obtained denoised ECG signal and N is the ECG signal length.

3. Experimental results

For our experiments, five different ECG signals were randomly selected from PhysioNet MIT-BIH Arrythmia Database [27] to evaluate the efficacy of the EMD–DWT, VMD-DWT and NML denoising approach. For each ECG signal, 1000 samples were chosen to conduct our study. The original ECG signal is added with Gaussian noise of variance 10 and 20 to obtain two noisy ECG signals. For the DWT thresholding-based approach, we considered the Daubechies-4 (DB4) and Symlet-4 (Sym4) as mother wavelets, and second and third level of decomposition [28]. For the simplicity of computations, the level of decomposition is set to five for both EMD and VMD. Fig. 1 illustrates an example of the original ECG signal and the same signal corrupted with a Gaussian noise with variance 10, and 20, respectively. Figs. 2 and 3 illustrate, respectively, some of the IMF and variational modes obtained by EMD and VMD of the original ECG signal shown in Fig. 1 corrupted with noise variance 10. Finally, Figs. 4 and 5 show the obtained denoised ECG signals when using DB4 and Sym4 wavelets, respectively.

Figure 1.

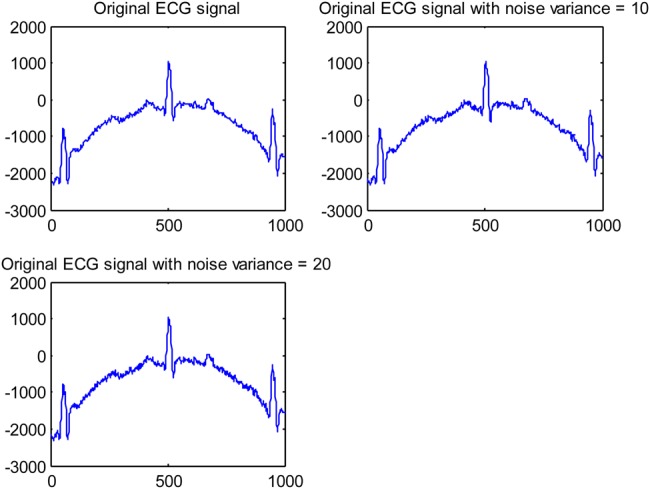
Example of original ECG signal and added Gaussian noise

Figure 2.

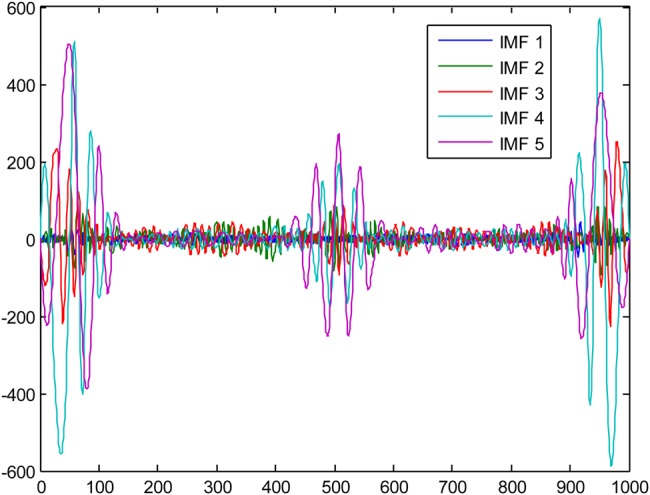
EMD results of the original ECG signal corrupted with noise variance set to 10

Figure 3.

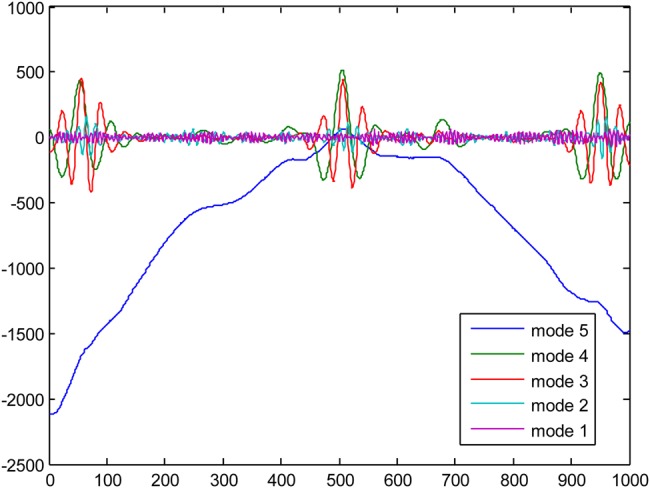
VMD results of the original ECG signal corrupted with noise variance set to 10

Figure 4.

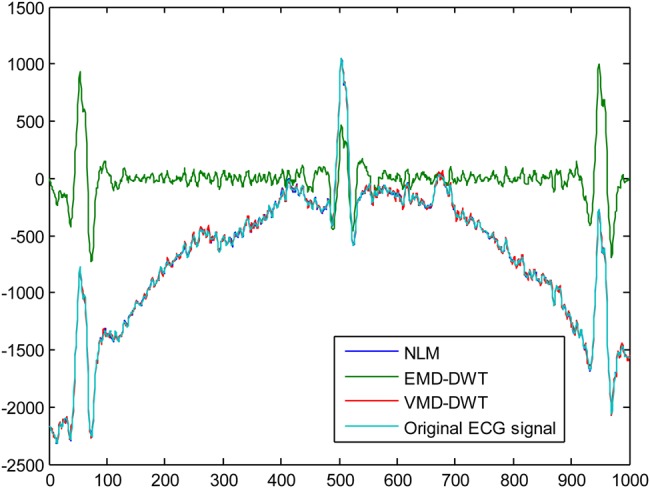
Denoising results using the DB4 wavelet of the original ECG signal corrupted with noise variance = 10

Figure 5.

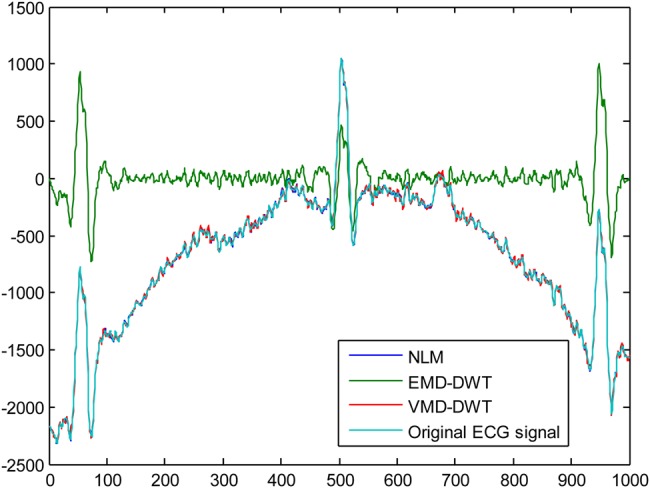
Denoising results using the Sym4 wavelet of the original ECG signal corrupted with noise variance = 10

Tables 1–20 provide the SNR and MSE values obtained by each approach. For better denoising performance, the SNR should be high, while the MSE should be low. The SNR values obtained with the NLM technique are given in Table 21. According to SNR and MSE values provided in Tables 1–20, the VMD-DWT outperforms the standard EMD–DWT model by using both DB4 and Sym4 wavelets in denoising the original ECG signal when it is affected with Gaussian noise of variance 10 and 20. In addition, these findings are confirmed at all DWT decomposition levels. Compared to non-local means denoising approach, the SNR and MSE values obtained and presented in Table 21 show that the NLM technique performs better than the EMD–DWT and VMD-DWT approaches for both types of noise levels. However, it is worth noting that, according to Figs. 4 and 5, the NLM and VMD-DWT achieved comparable performances.

Table 2.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: first ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	3.2753	3.2753	3.2753
EMD-Sym4	MSE	30828.5871	30828.2766	30828.1463
VMD-Sym4	SNR	23.5495	23.5598	23.5501
VMD-Sym4	MSE	289.4219	288.7344	289.3812

Table 3.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: first ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-DB4	SNR	2.8907	2.8906	2.8906
EMD-DB4	MSE	33683.2170	33683.3671	33683.6512
VMD-DB4	SNR	15.3692	15.3736	15.3739
VMD-DB4	MSE	1903.5285	1901.5999	1901.4763

Table 4.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: first ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	2.8907	2.8906	2.8906
EMD-Sym4	MSE	33683.0990	33683.4726	33683.4988
VMD-Sym4	SNR	15.3706	15.3744	15.3748
VMD-Sym4	MSE	1902.9217	1901.2602	1901.0757

Table 5.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: second ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-DB4	SNR	5.0057	5.0058	5.0058
EMD-DB4	MSE	20696.9580	20696.5336	20696.5801
VMD-DB4	SNR	21.2452	21.2548	21.2550
VMD-DB4	MSE	491.9994	490.9134	490.8844

Table 6.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: second ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	5.0057	5.0058	5.0058
EMD-Sym4	MSE	20697.0722	20696.5657	20696.5026
VMD-Sym4	SNR	21.2421	21.2535	21.2539
VMD-Sym4	MSE	492.3405	491.0562	491.0080

Table 7.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: second ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-DB4	SNR	4.9510	4.9511	4.9511
EMD-DB4	MSE	20959.4596	20959.0742	20958.9975
VMD-DB4	SNR	19.2211	19.2249	19.2270
VMD-DB4	MSE	784.1001	783.4102	783.0280

Table 8.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: second ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	4.9510	4.9510	4.9511
EMD-Sym4	MSE	20959.6115	20959.2916	20959.1142
VMD-Sym4	SNR	19.2205	19.2241	19.2262
VMD-Sym4	MSE	784.2097	783.5511	783.1767

Table 9.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: third ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-DB4	SNR	1.5224	1.5224	1.5224
EMD-DB4	MSE	93050.8652	93050.4269	93050.3656
VMD-DB4	SNR	20.8326	20.8575	20.8519
VMD-DB4	MSE	541.0246	537.9388	538.6231

Table 10.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: third ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	1.5224	1.5224	1.5224
EMD-Sym4	MSE	93050.6676	93050.2675	93050.1997
VMD-Sym4	SNR	20.8324	20.8545	20.8389
VMD-Sym4	MSE	541.0549	538.3017	540.2384

Table 11.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: third ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-DB4	SNR	1.5329	1.5328	1.5328
EMD-DB4	MSE	93275.1847	93274.6451	93274.6000
VMD-DB4	SNR	17.0451	17.0455	17.0471
VMD-DB4	MSE	1294.1005	1293.9791	1293.5158

Table 12.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: third ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	1.5329	1.5328	1.5328
EMD-Sym4	MSE	93275.0055	93274.5262	93274.3113
VMD-Sym4	SNR	17.0457	17.0460	17.0487
VMD-Sym4	MSE	1293.9227	1293.8423	1293.0246

Table 13.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: fourth ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-DB4	SNR	3.0218	3.0218	3.0218
EMD-DB4	MSE	131418.6073	131418.5735	131418.5741
VMD-DB4	SNR	28.7612	28.7595	28.5845
VMD-DB4	MSE	87.1689	87.2021	90.7890

Table 14.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: fourth ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	3.0218	3.0218	3.0218
EMD-Sym4	MSE	131418.5666	131418.5632	131418.6665
VMD-Sym4	SNR	28.7581	28.7673	28.7417
VMD-Sym4	MSE	87.2300	87.0465	87.5612

Table 15.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: fourth ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-DB4	SNR	3.0546	3.0545	3.0545
EMD-DB4	MSE	132414.4638	132;414.2288	132413.9752
VMD-DB4	SNR	16.0172	16.0406	16.0194
VMD-DB4	MSE	1639.6700	1630.8619	1638.8607

Table 16.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: fourth ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	3.0546	3.0546	3.0546
EMD-Sym4	MSE	132414.5087	132414.3851	132414.4224
VMD-Sym4	SNR	16.0206	16.0383	16.0268
VMD-Sym4	MSE	1638.3949	1631.7233	1636.0790

Table 17.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: fifth ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-DB4	SNR	10.9169	10.9169	10.9169
EMD-DB4	MSE	809421.5499	809421.3385	809421.2257
VMD-DB4	SNR	22.5746	22.5966	22.5719
VMD-DB4	MSE	362.2579	360.4261	362.4816

Table 18.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: fifth ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	10.9169	10.9169	10.9169
EMD-Sym4	MSE	809421.3898	809421.0519	809421.2054
VMD-Sym4	SNR	22.5717	22.5914	22.5722
VMD-Sym4	MSE	362.4999	360.8572	362.4583

Table 19.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: fifth ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-DB4	SNR	10.9942	10.9942	10.9942
EMD-DB4	MSE	823954.7781	823954.5903	823953.3942
VMD-DB4	SNR	14.7856	14.7963	14.7915
VMD-DB4	MSE	2177.3058	2171.9394	2174.3733

Table 1.

SNR and MSE values depending on the DWT decomposition level using the DB4 wavelet: first ECG signal with noise variance 10

		Level 1	Level 2	Level 3
EMD–DB4	SNR	3.2753	3.2753	3.2753
EMD–DB4	MSE	30828.5930	30828.1368	30828.0466
VMD-DB4	SNR	23.5503	23.5597	23.5474
VMD-DB4	MSE	289.3658	288.7396	289.5618

Table 20.

SNR and MSE values depending on the DWT decomposition level using the Sym4 wavelet: fifth ECG signal with noise variance 20

		Level 1	Level 2	Level 3
EMD-Sym4	SNR	10.9942	10.9942	10.9942
EMD-Sym4	MSE	823955.0717	823954.9560	823954.7459
VMD-Sym4	SNR	14.7846	14.7969	14.7925
VMD-Sym4	MSE	2177.8341	2171.6420	2173.8296

Table 21.

SNR and MSE values based on the NLM technique

ECG signals	Performance metric	Noise variance = 10	Noise variance = 20
1st	SNR	28.27660	22.12515
1st	MSE	97.45846	401.75795
2nd	SNR	28.23162	22.42448
2nd	MSE	98.47328	375.00076
3rd	SNR	28.34325	22.28176
3rd	MSE	95.97435	387.52915
4th	SNR	28.50518	22.65744
4th	MSE	92.46176	355.41536
5th	SNR	28.18979	22.46675
5th	MSE	99.42625	371.36861

4. Conclusion

A number of studies have taken advantage of the hybrid EMD–DWT approach for ECG signal enhancement. In such an approach, the EMD is employed as an adaptive technique for ECG decomposition, whereas the DWT is used for denoising based on a given thresholding criterion. Recently, the VMD has been proposed as an adaptive multiresolution technique to overcome some of the limits of the EMD such as sensitivity to noise. This Letter compared the EMD–DWT against the VMD-DWT approach in denoising a real ECG signal, corrupted with three levels of Gaussian noise. Indeed, this Letter is the first to apply VMD in the problem of ECG signal denoising. We relied on adaptive multiresolution techniques (EMD, VMD) for ECG decomposition because of their ability to adjust to unknown signal characteristics varying over time. For comparison purposes, the non-local means algorithm is used for denoising a noisy ECG signal. Five ECG signals obtained from PhysioNet were chosen to conduct our study. Experimental results evaluated by using SNR and MSE showed that the best performance was obtained by the NLM technique followed by the VMD-DWT approach. However, they achieved comparable performances. The conventional EMD–DWT techniques performed the worst.

Our study can be extended in future work by considering different values used to determine the number of variational modes used to obtain results. Indeed, the VMD is still faced with the difficulty of parameter choice, which will be our further research avenue for the application and improvement of the VMD-DWT technique. As this Letter presents a preliminary study, future work will also consider other types of biological signals.