Joint Design of Large-Tip-Angle Parallel RF Pulses and Blipped Gradient Trajectories

Abstract

Purpose

To design multichannel large-tip-angle k_T-points and spokes radiofrequency pulses and gradient waveforms for transmit field inhomogeneity compensation in high field MRI.

Theory and Methods

An algorithm to design RF subpulse weights and gradient blip areas is proposed to minimize a magnitude least-squares cost function that measures the difference between realized and desired state parameters in the spin domain, and penalizes integrated RF power. The minimization problem is solved iteratively with interleaved target phase updates, RF subpulse weights updates using the conjugate gradient method with optimal control-based derivatives, and gradient blip area updates using the conjugate gradient method. Two-channel parallel transmit simulations and experiments were conducted in phantoms and human subjects at 7 T to demonstrate the method and compare it to small-tip-angle-designed pulses and circularly-polarized excitations.

Results

The proposed algorithm designed more homogeneous and accurate 180° inversion and refocusing pulses than other methods. It also designed large-tip-angle pulses on multiple frequency bands with independent and joint phase relaxation. Pulses designed by the method improved specificity and CNR in a finger-tapping spin echo BOLD fMRI study, compared to circularly-polarized mode refocusing.

Conclusion

A joint RF and gradient waveform design algorithm was proposed and validated to improve large-tip-angle inversion and refocusing at ultra-high field.

Introduction

Transmit radiofrequency (RF) field $(B_1^{+})$ inhomogeneity creates spatially-varying contrast and local signal voids, posing a challenge for high field MRI. It can be mitigated by multi-dimensional spokes [1] and k_T-points pulses [2] RF pulses, optionally in combination with parallel transmission [3, 4]. Those pulses comprise short trains of RF subpulses that have the same shape but are weighted by unique amplitudes and phases, and are interleaved with gradient blips that move the pulses’ trajectory to different excitation k-space locations [5]. They have been demonstrated to be capable in compensating $B_1^{+}$ field inhomogeneities in slice-selective (spokes) and volumetric (k_T-points) excitation. Spokes and k_T-points pulse designs have been mainly formulated in the small-tip-angle (STA) regime [5], in which the spatial flip angle pattern produced by the pulses are approximately linear functions of their subpulse weights. However, designing large-tip-angle (LTA) pulses such as 180° refocusing pulses for spin echo (SE) sequences or inversion pulses for inversion recovery sequences using the STA approximation can lead to significant errors in the excited flip angle patterns, due to Bloch equation nonlinearity at large tip angles.

To overcome the limits of STA-based pulse designs for LTA excitations, a number of LTA pulse design algorithms have been proposed that apply or could apply to the spokes and k_T-points pulse design problems [6–11], and are based on different optimization methods and ways to approximate the non-linear Bloch equation. With the exception of Refs. [10] and [11], they require the gradient trajectory to be designed a priori using an STA-based method or heuristics, and do not further optimize the trajectory to improve the overall LTA excitation. Of note among these are an algorithm that was formulated for LTA spokes pulse design and uses a coordinate descent algorithm to iteratively optimize the RF subpulse weights one-by-one [6], and LTA k_T-points pulse design algorithms based on optimal control [10], and gradient ascent pulse engineering [11].

Here, an alternative magnitude-least squares spin-domain algorithm for joint RF and gradient blipped LTA pulse design is described. The algorithm updates RF subpulse weights using the conjugate gradient algorithm with optimal control derivative calculations [12], and the gradient blips using the conjugate gradient algorithm. It can design pulses on one or multiple resonant frequencies. It is validated and compared to STA-designed pulses in in vivo simulations at 7 and 14 Tesla (T), and in phantom and in vivo anatomical scans at 7 T. The algorithm is also used to design pulses for an SE BOLD fMRI study at 7 T. Preliminary accounts of this work were reported at the 2009 ISMRM Workshop on Parallel MRI and the 2010 and 2013 ISMRM meetings [13–15].

Theory

Pulse design problem formulations

The proposed algorithm will design spokes and k_T-points RF pulses comprising trains of slice-selective or hard subpulses, each played simultaneously on multiple transmit channels with different amplitudes and phases. It will also design accompanying 2D or 3D gradient waveforms with optimized phase encoding blips between the RF subpulses, and in the spokes case slice-select gradient trapezoids will be played during the subpulses. This section describes how the spatial excitation patterns produced by the pulses are calculated and how the desired excitation patterns are formed, and then introduces the magnitude least-squares pulse design problem formulation.

The small-excitation approximation [16] does not generally hold for LTA RF pulses played on spokes and k_T-points trajectories, so the Bloch equation must be numerically evaluated to calculate their excitation patterns. The proposed algorithm is based on the spin-domain Bloch equation with the hard pulse approximation [17]. Spin-domain rotations are represented by two parameters, α and β, that respectively represent rotations about the longitudinal and transverse components of the total magnetic field. Given a multidimensional pulse comprising gradient and multichannel RF waveforms, the rotation parameters (α, β) for the entire pulse at location r⃗ = (x, y, z) and frequency offset f are given by:

$$\left(\begin{array}{c}\hfill \alpha \hfill \\ \hfill \beta \hfill \end{array}\right)=\left(\begin{array}{cc}\hfill A_{N_s}\hfill & \hfill -B_{N_s}^{*}\hfill \\ \hfill B_{N_s}\hfill & \hfill A_{N_s}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z_{N_s-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z_{N_s-1}^{*}\hfill \end{array}\right)\dots \left(\begin{array}{cc}\hfill z_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z_1^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill A_1\hfill & \hfill -B_1^{*}\hfill \\ \hfill B_1\hfill & \hfill A_1^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),$$ [1]

where

$$z_s=\text{exp}(\frac{\iota \gamma }{2}\overrightarrow{r}·{\overrightarrow{g}}_s),s=1,\dots ,N_s-1,$$ [2]

are the phase shifts applied by the N_s − 1 gradient blips between the N_s subpulses, and the (A_s, B_s) are the (α, β) parameters of each length-N_t subpulse, given by:

$$\left(\begin{array}{c}\hfill A_s\hfill \\ \hfill B_s\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill z\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill C_{N_t}\hfill & \hfill -S_{N_t}^{*}\hfill \\ \hfill S_{N_t}\hfill & \hfill C_{N_t}\hfill \end{array}\right)\dots \left(\begin{array}{cc}\hfill z\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill C_1\hfill & \hfill -S_1^{*}\hfill \\ \hfill S_1\hfill & \hfill C_1\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),$$ [3]

where

$$z=\text{exp}(\iota \pi f{\mathrm{\Delta }}_t)$$ [4]

is the phase shift caused by the frequency offset at each time step and

$$C_t=\text{cos}\left(\frac{\gamma {\mathrm{\Delta }}_t}{2}\right|p_t\sum _{c=1}^{N_c}{S}_c(\overrightarrow{r})b_{cs}\left|\right),$$ [5]

$$S_t=\iota \text{exp}(\iota \angle p_t\sum _{c=1}^{N_c}{S}_c(\overrightarrow{r})b_{cs})\text{sin}\left(\frac{\gamma {\mathrm{\Delta }}_t}{2}\right|p_t\sum _{c=1}^{N_c}{S}_c(\overrightarrow{r})b_{cs}\left|\right),$$ [6]

are the α and β parameters for each subpulse time point and spatial location. In these equations $\iota =\sqrt{-1}$, Δ_t is the dwell time with which the RF and gradient waveforms are sampled, g⃗_s is the area of gradient blip s, f is a constant frequency offset due to off-resonance or chemical shift, p_t is the t-th sample of the RF subpulse waveform (a hard pulse for k_T-points or a slice-selective pulse for spokes), S_c(r⃗) is transmit channel c’s complex-valued $B_1^{+}$ field at r⃗, and b_cs is channel c’s complex-valued weight for spoke s. The definition of z in Eq. 4 is based on the assumption that either a) no gradient waveforms are played simultaneously with the RF subpulses, as is the case for k_T-points pulses, or that b) slice-select trapezoids are played simultaneously with the subpulses, as is the case for spokes pulses, but that only the center of the excited slice is considered when optimizing the subpulse weights, where the subpulses are on-resonance so the gradient rotations drop out of the equations. Upon evaluating (α, β) at each spatial location and frequency of interest, the excitation, inversion, saturation, and refocusing patterns produced by the pulses can be calculated using relationships given in Ref. [17].

The variables to be designed include the N_cN_s RF subpulse weights ${\{b_{cs}\}}_{c,n=1}^{N_c,N_s}$, and the 2(N_s − 1) x- and y-gradient blip areas ${\{{\overrightarrow{g}}_s\}}_{s=1}^{N_s-1}$ for spokes and 2D k_T-points pulses, or the 3(N_s − 1) x-, y-, and z-gradient blip areas for 3D k_T-points pulses. The objective of the design is to produce excitation patterns that are as close as possible to desired patterns over N_x spatial locations. For spokes and 2D k_T-points designs, the spatial locations are usually in the transverse plane at the center of the target slice. For 3D k_T-points designs they sample a 3D volume. For multifrequency designs, N_f resonance frequency offsets are also included for each spatial location [18, 19]. The desired spinor excitation pattern vectors (α^d, β^d) must be specified over the N_x spatial locations ${\{{\overrightarrow{r}}_i\}}_{i=1}^{N_x}$ and N_f frequencies ${\{f_j\}}_{j=1}^{N_f}$. However, it is more intuitive to specify a target flip angle pattern and calculate (α^d, β^d) from that. Given a length-N_xN_f target flip angle pattern vector θ^d, the corresponding (α^d, β^d) are:

$${\alpha }_{ij}^d=\text{cos}({\theta }_{ij}^d/2),$$ [7]

$${\beta }_{ij}^d=\text{sin}({\theta }_{ij}^d/2).$$

With these definitions, a regularized magnitude least-squares cost function [20, 21] can be specified as:

$$\mathrm{\Psi }(\mathit{b},\overrightarrow{\mathit{g}})=\frac{1}{2}{\Vert |\mathit{\alpha }(\mathit{b},\overrightarrow{\mathit{g}})|-{\mathit{\alpha }}^d\Vert }^2+\frac{1}{2}{\Vert |\mathit{\beta }(\mathit{b},\overrightarrow{\mathit{g}})|-{\mathit{\beta }}^d\Vert }^2+\frac{\lambda }{2}{\Vert \mathit{b}\Vert }^2.$$ [8]

where λ ‖b‖² penalizes integrated RF power with tunable regularization parameter λ. In the present algorithm the magnitude operators are replaced by auxiliary target excitation phase patterns (ϕ^α, ϕ^β) that are optimized along with the RF weights and gradient blip areas, resulting in the equivalent cost function:

$$\mathrm{\Psi }(\mathit{b},\overrightarrow{\mathit{g}},{\mathit{\varphi }}^{\alpha },{\mathit{\varphi }}^{\beta })=\frac{1}{2}{\Vert \mathit{\alpha }(\mathit{b},\overrightarrow{\mathit{g}})-{\mathit{\alpha }}^d({\mathit{\varphi }}^{\alpha })\Vert }^2+\frac{1}{2}{\Vert \mathit{\beta }(\mathit{b},\overrightarrow{\mathit{g}})-{\mathit{\beta }}^d({\mathit{\varphi }}^{\beta })\Vert }^2+\frac{\lambda }{2}{\Vert \mathit{b}\Vert }^2$$ [9]

where

$${\{{\mathit{\alpha }}^d({\mathit{\varphi }}^{\alpha })\}}_{ij}={\alpha }_{ij}^d{e}^{{\varphi }_{ij}^{\alpha }},$$ [10]

$${\{{\mathit{\beta }}^d({\mathit{\varphi }}^{\beta })\}}_{ij}={\beta }_{ij}^d{e}^{{\varphi }_{ij}^{\beta }}.$$ [11]

Equations 8 and 9 represent an ‘independent-phase’ formulation analogous to Eq. 4 in Ref. [19], wherein the target phase patterns are independently optimized for each frequency. A ‘joint-phase’ formulation is also possible in analogy to Eq. 5 in Ref. [19], wherein a single spatial phase pattern is jointly determined for all frequencies, but each frequency is given a constant phase shift that is also optimized. In both formulations, the cost function is minimized by alternating between the variables and updating each one while holding the others fixed. In the following sections the update strategies for the RF weights b and the gradient blip areas g⃗ are described. The reader is referred to Ref. [19], Eqs. 6–8 for a full description of the target phase pattern updates for both the independent- and joint-phase formulations.

Updating the RF subpulse weights

The RF subpulse weights are updated using an optimal control derivative calculations with a conjugate gradient algorithm and a backtracking line search. The search direction vector Δb contains approximate derivatives of the cost function with respect to the real and imaginary parts of each weight, denoted $b_{cs}^R$ and $b_{cs}^I$. The derivative with respect to $b_{cs}^R$ is:

$$\frac{\partial \mathrm{\Psi }}{\partial b_{cs}^R}=\sum _{i,j=1}^{N_x,N_f}\Re \left\{{\left(\frac{\partial {\alpha }_{ij}}{\partial b_{cs}^R}\right)}^{*}\right({\alpha }_{ij}-{\alpha }_{ij}^d({\varphi }_{ij}^{\alpha }))+{\left(\frac{\partial {\beta }_{ij}}{\partial b_{cs}^R}\right)}^{*}({\beta }_{ij}-{\beta }_{ij}^d({\varphi }_{ij}^{\beta })\left)\right\}+\lambda b_{cs}^R,$$ [12]

where the ℜ{·} operator returns the real part of a complex number, and the dependence of α_ij and β_ij on (b, g⃗) has been suppressed for brevity. Calculating $(\frac{\partial {\alpha }_{ij}}{\partial b_{cs}^R},\frac{\partial {\beta }_{ij}}{\partial b_{cs}^R})$ and $(\frac{\partial {\alpha }_{ij}}{\partial b_{cs}^I},\frac{\partial {\beta }_{ij}}{\partial b_{cs}^I})$ requires some computation, since each weight b_cs appears in the N_t consecutive RF rotation matrices of the subpulse it applies to, so those partial derivatives contain sums over N_t terms of the form:

$$\left(\begin{array}{c}\hfill {\left\{\frac{\partial {\alpha }_{ij}}{\partial b_{cs}^R}\right\}}_t\hfill \\ \hfill {\left\{\frac{\partial {\beta }_{ij}}{\partial b_{cs}^R}\right\}}_t\hfill \end{array}\right)\approx \left(\begin{array}{cc}\hfill {\alpha }^R\hfill & \hfill -{({\beta }^R)}^{*}\hfill \\ \hfill {\beta }^R\hfill & \hfill {({\alpha }^R)}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 0\hfill & \hfill \frac{\iota \gamma {\mathrm{\Delta }}_t}{2}{p}_t^{*}{S}_c^{*}({\overrightarrow{r}}_i)\hfill \\ \hfill \frac{\iota \gamma {\mathrm{\Delta }}_t}{2}{p}_t{S}_c({\overrightarrow{r}}_i)\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right)$$ [13]

$$\left(\begin{array}{c}\hfill {\left\{\frac{\partial {\alpha }_{ij}}{\partial b_{cs}^I}\right\}}_t\hfill \\ \hfill {\left\{\frac{\partial {\beta }_{ij}}{\partial b_{cs}^I}\right\}}_t\hfill \end{array}\right)\approx \left(\begin{array}{cc}\hfill {\alpha }^R\hfill & \hfill -{({\beta }^R)}^{*}\hfill \\ \hfill {\beta }^R\hfill & \hfill {({\alpha }^R)}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 0\hfill & \hfill \frac{\gamma {\mathrm{\Delta }}_t}{2}{p}_t^{*}{S}_c^{*}({\overrightarrow{r}}_i)\hfill \\ \hfill -\frac{\gamma {\mathrm{\Delta }}_t}{2}{p}_t{S}_c({\overrightarrow{r}}_i)\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right),$$ [14]

where t indexes the subpulse samples, (α^R, β^R) are the ‘reverse’ parameters representing all rotations at spatial location r⃗_i and frequency f_j that follow this time point, including rotations by all subsequent subpulses, and (α^F, β^F) are the ‘forward’ parameters representing all rotations that precede this time point, including rotations by all preceding subpulses. These approximate derivatives can be derived by replacing an RF rotation matrix with its first-order Taylor series approximation around a zero rotation, and then calculating its first derivative with respect to its RF subpulse weight. Δb can be calculated efficiently using an algorithm that loops through time points, evaluating Eqs. 13 and 14 for each one and updating (α^R, β^R) and (α^F, β^F) in-between evaluations [12]. The algorithm’s computational cost is equal to that of two Bloch simulations. Further details are provided in the Appendix. Once Δb is calculated, a step size is a determined using a backtracking line search [22], and the weights are updated as: b ← b − aΔb. As is the case when evaluating the pulse’s excitation patterns (Eqs. 1–6), all calculations can proceed in parallel across the spatial locations and frequency offsets, and the resulting search directions can be summed afterwards.

Updating the gradient blips

Similar to the RF subpulse weight updates, the gradient blip areas are updated using conjugate gradient with a backtracking line search. The derivative of the cost function with respect to blip s’s x-component $g_s^x$ is:

$$\frac{\partial \mathrm{\Psi }}{\partial g_s^x}=\sum _{i,j=1}^{N_x,N_f}\Re \left\{{\left(\frac{\partial {\alpha }_{ij}}{\partial g_s^x}\right)}^{*}\right({\alpha }_{ij}-{\alpha }_{ij}^d({\varphi }_{ij}^{\alpha }))+{\left(\frac{\partial {\beta }_{ij}}{\partial g_s^x}\right)}^{*}({\beta }_{ij}-{\beta }_{ij}^d({\varphi }_{ij}^{\beta })\left)\right\}.$$ [15]

The partial derivatives will have the form:

$$\left(\begin{array}{c}\hfill \frac{\partial {\alpha }_{ij}}{\partial g_s^x}\hfill \\ \hfill \frac{\partial {\beta }_{ij}}{\partial g_s^x}\hfill \end{array}\right)=\frac{\iota \gamma }{2}{x}_i\left(\begin{array}{cc}\hfill {\alpha }^R\hfill & \hfill -{({\beta }^R)}^{*}\hfill \\ \hfill {\beta }^R\hfill & \hfill {({\alpha }^R)}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill \text{exp}(\frac{\iota \gamma }{2}{\overrightarrow{r}}_i·{\overrightarrow{g}}_s)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\text{exp}(-\frac{\iota \gamma }{2}{\overrightarrow{r}}_i·{\overrightarrow{g}}_s)\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right).$$ [16]

The derivatives are efficiently calculated using the same approach as for the RF subpulse weights, by defining forward and reverse spinors and working backwards. Further details on that method are provided in the Appendix. Once the search direction vector Δg⃗ is filled, a backtracking line search is used to approximately determine the best step size a within a predefined maximum blip area radius, and the areas are updated as: g⃗ ← g⃗ − aΔg⃗. To accelerate the update, the spinors ${\{(A_s,B_s)\}}_{s=1}^{N_s}$ for each RF subpulse returned by the RF subpulse weight update are used in all gradient blip update calculations, since they do not change during the gradient blip update. Thus, the computational cost of one gradient blip update iteration is approximately N_t times smaller than the cost of one RF subpulse weight update iteration.

Methods

Algorithm Implementation

The algorithm was implemented in MATLAB R2013a (Mathworks Inc., Natick, MA, USA), with multi-threaded Bloch equation evaluations and derivative calculations implemented in C, and called using MATLAB’s MEX interface. The RF and gradient waveforms were sampled with a 6.4 µs dwell time, and gradient trapezoids were designed subject to a maximum amplitude of 5 mT/m and a maximum slew rate of 80 mT/m/s. Slice-selective spokes subpulses were designed using the Shinnar-Le Roux algorithm [17]. The RF subpulse weights and gradient blip areas were initialized using a small-tip-angle blipped pulse design algorithm [19]. The integrated RF power regularization parameter λ was initialized so as to balance the excitation error and integrated power terms in Eq. 8 based on the initial Bloch-simulated flip angle patterns. Every 10 iterations the algorithm checked whether one of the terms was 25% larger than the other, and if so λ was re-computed to re-balance the terms. The target excitation phase patterns were initialized to zero but were updated prior to any RF subpulse weight and gradient blip updates, using the α and β patterns of the initial subpulse weights and gradient blip areas. Up to 20 Polak-Ribiere conjugate gradient iterations were used for each update of the RF subpulse weights and each update of the gradient blip areas. The algorithm stopped when the cost decreased by less than 0.1% between consecutive iterations. Execution time for the algorithm on a 3 GHz Core i7 Macbook Pro computer with 16 GB RAM was 10 seconds for a two-channel 5-k_T-point 180° pulse using in vivo field maps, with 21 outer iterations to convergence. A 3-spoke 180° pulse design with the same field maps took 20 seconds with 21 outer iterations to convergence, and a 5-spoke 180° pulse design took 28 seconds with 21 outer iterations to convergence. Within each outer iteration, the RF weight update comprised approximately 90% of the compute time, and the gradient blip update comprised the other 10%. The algorithm code and several examples are available at https://bitbucket.org/wgrissom/blipped-large-tip-angle-rf-pulse-design/downloads. That software package includes Bloch equation and derivative calculation functions in C and CUDA; the execution times listed above used the multithreaded C functions with 4 threads.

Simulations

Simulations were performed using two-channel $B_1^{+}$ and off resonance maps measured from 6 healthy human subjects. The subjects were imaged with approval of the Institutional Review Board at Vanderbilt University using a 7 T Philips Achieva human MRI scanner (Philips Healthcare, Cleveland, OH, USA) with a two-channel birdcage head coil for parallel transmission and a 32-channel head coil for parallel reception (both coils from Nova Medical Inc., Wilmington, MA, USA). Maps were collected from three slices spaced 15 mm apart with 4 × 4 mm² in-plane voxel size, 256 × 256 mm² FOV, and 3 mm slice thickness, using “STE first” DREAM for $B_1^{+}$ mapping [23], and the delayed-TE method for off resonance mapping [24].

Single-frequency 180° spokes refocusing pulses were designed separately for each slice in each subject. In addition, 90° spokes excitation and 180° refocusing pulses were designed for single-slice $B_1^{+}$ and off resonance maps simulated with 8 transmit channels at 14 T [25]. All pulses used bipolar z-gradient trajectories and slice-selective subpulses that were 0.7 ms long, had a time-bandwidth product of 2, and excited 3 mm-thick slices. The subpulse duration included the entire duration of each subpulse’s slice-select trapezoid. RF was played only during the flat portions of the trapezoids, and phase-encoding blips were centered midway between consecutive slice-select trapezoids, with no additional time delays. Multi-frequency pulse designs were also performed using the two-channel $B_1^{+}$ and off resonance maps. The pulse designs targeted a 180° flip angle with 17 frequency bands uniformly distributed between −400 and +400 Hz (50 Hz band separation), with 2D k_T-points trajectories and independent phase updates. The hard RF subpulses were 0.1 ms long, and were separated by 0.18 ms to accommodate phase encoding gradient blips. The designs were initialized by and compared to multifrequency STA designs that also used independent phase updates [19].

Experiments

The same 7T scanner, coils, and field mapping sequences were used for phantom and human experiments. First, single-frequency 180° 2D k_T-points pulses for refocusing were designed using STA and LTA methods for an axial slice of a 20 cm silicone ball phantom. The pulses comprised 5 RF subpulses that were 0.3 ms long and were separated by 0.18 ms to accommodate phase encoding gradient blips. To measure their refocusing patterns, the pulses were used in an SE sequence (15 ms TE, 3 s TR, 4 × 4 mm² voxel size, 256 × 256 mm² FOV, 5-spoke STA-designed 90° excitation pulse with 3 mm slice thickness). A circularly-polarized (CP)-mode hard pulse refocusing pattern was also measured. To divide out the excitation and receive field map patterns, a gradient echo (GRE) image was collected with the same protocol but with a 2 ms TE. The same overall procedure was then followed for a dual-frequency k_T-points refocusing experiment. For that experiment, four 2D 7-k_T-points pulses were designed with 0.3 ms-long subpulses, STA or LTA design, and independent or joint phase updates between the two frequency bands (0 and 400 Hz). The pulses were used in SE sequences (2 × 2 mm² in-plane voxel size, 256 × 256 mm² FOV, 5-spoke STA-designed dual-frequency 90° excitation with 3 mm slice thickness, 3 s TR, 32 ms TE). Images were acquired at the two frequencies by changing the spectrometer center frequency. GRE images were also acquired with the same same protocol as the SE sequence, except with a shorter 10 ms TE. The refocusing patterns for each frequency band and refocusing pulse were obtained by dividing the SE images by the corresponding GRE image at the same frequency. Flyback trajectories (where RF is played only during positive gradient lobes and negative gradient lobes are designed to have minimum durations) were used for the STA-designed spokes excitation pulses since we have empirically found that bipolar spokes pulses are somewhat more prone to excitation errors due to gradient waveform errors and eddy currents [26]. Finally, 5-spoke single-frequency 180° inversion pulses were designed using STA and LTA methods with bipolar slice-selective gradient trajectories, subpulse time-bandwidth product 4, subpulse duration 2.8 ms, and slice thickness 7 mm. To measure their inversion patterns, the pulses were used in an inversion recovery GRE sequence (8 ms TE, 8.7 ms TI, 3 s TR, 4 × 4 mm² in-plane voxel size, CP-mode excitation with 3 mm slice thickness). To divide out the excitation and receive field map patterns, a third GRE image was acquired with no inversion pulse.

In vivo anatomical and fMRI experiments were then performed in healthy male volunteers. In the anatomical experiments, 2D k_T-points refocusing pulses were designed using the same parameters as in the phantom experiments, and images were acquired using the pulses in an SE sequence (50 ms TE, 1 s TR, 1 × 1 mm² voxel size, 190 × 190 mm² FOV, 3-spoke flyback STA-designed 90° excitation pulse with 3 mm slice thickness). SE and GRE BOLD fMRI experiments were then performed. The GRE BOLD acquisition used a conventional time-bandwidth product 4 90° excitation. The SE BOLD acquisitions used either the same excitation as the GRE BOLD acquisitions plus a 1.4 ms-long CP-mode hard pulse for refocusing (‘CP’ case), or 3-spoke flyback excitation with time-bandwidth product 4 plus 5 ms-long 5-k_T point refocusing (‘LTA’ case). The LTA SE sequence is illustrated in Fig. 6a. All acquisitions used 2.5 mm excitation slice thickness. EPI readouts were used with 1.6 × 1.6 mm² in-plane voxel size and 3 s TR. The GRE acquisition used 25 ms TE, and the SE acquisitions used 50 ms TE, which were chosen to match the previously-measured tissue $T_2^{*}$ and T₂, respectively [27–29]. SAR Calculations were handled by vendor-provided software running on the scanner’s host PC, which used lookup table operations to calculate the incremental SAR due to each time point of the pulses based on the two transmit channels’ relative amplitude and phase. The scanner used the results of those calculations to enforce SAR limits by setting a minimum selectable TR. Acquisitions were performed during a neuronal (finger tapping) task for a slice centered on the primary motor cortex (21s/12s off/on, 3 repetitions, 1 Hz finger tapping). Data were corrected for motion and baseline drift, and activation maps (z > 4.0) were calculated using standard multiple regression and non-parametric autocorrelation routines. To prevent sensitivity bias to draining veins which are expected to provide different contrast in SE compared to GRE, an ROI in cortical gray matter with breath hold and in the primary motor cortex with finger tapping was drawn, and regions of large veins were excluded. With mean signal S and signal change ΔS, the timecourse contrast-to-noise ratio (CNR = ΔS/σ) was calculated for each sequence.

Figure 6.

(a) Illustration of the LTA SE sequence with spokes excitation and k_T-points refocusing. (b) BOLD images and (c) right-handed finger-tapping activation map overlaid for GRE, CP mode refocusing SE and LTA-designed k_T-points refocusing SE. (d) Shows zoomed activation maps in the left primary motor cortex. The GRE map shows robust activation across motor regions, yet is relatively non-specific to the cortical ribbon. The CP map shows little activation, which may be consistent with poor refocusing performance. The LTA map shows relatively robust activation compared to CP, which also appears to co-localize more closely with primary motor cortex than GRE. This observation is consistent with reduced sensitivity of 7T SE fMRI to extravascular BOLD effects around draining veins relative to GRE.

Results

Simulations

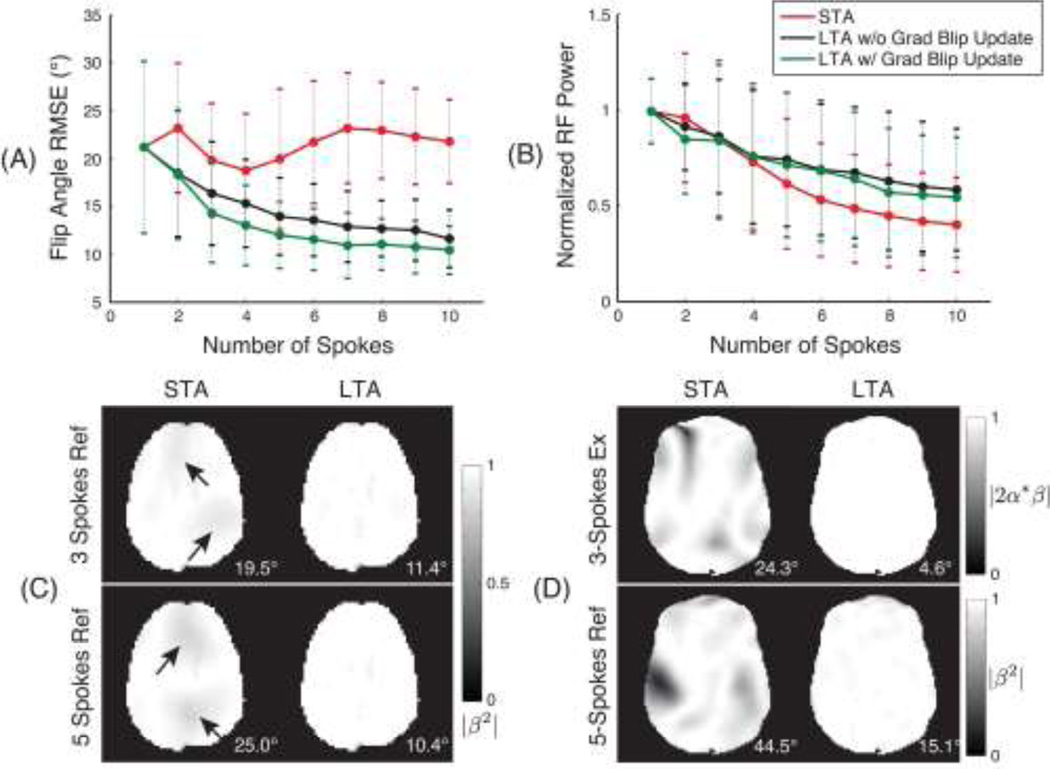
Figure 1 shows the single-frequency simulation results. The LTA designs achieved consistently lower flip angle RMSE, by an average 50% margin that increased with increasing numbers of spokes. The integrated RF power of the LTA pulses was generally higher than the STA pulses, but by a smaller average margin. The plots also show that joint gradient optimization did significantly improve flip angle RMSE compared to RF optimization alone, and slightly reduced integrated RF power. Figure 1c shows representative refocusing (|β²|) patterns illustrating how STA-designed pulses can produce increasingly inhomogeneous LTA excitations as the number of spokes is increased. In that example the addition of 2 spokes (from 3 to 5) introduced new refocusing errors in the STA case, but an improvement in the LTA case. Figure 1d shows the 8-channel 14 T results, where both the 3-spoke excitation pattern (|2α*β|) and 5-spoke refocusing patterns were substantially improved by the LTA design. Because λ is initialized to balance the initial excitation error and RF power, and is typically updated no more than twice over the LTA design iterations, the LTA algorithm tends to preserve the initial pulse’s error-power balance. Supporting Figure S1 illustrates this for a k_T-points 180° pulse design, by comparing error-power coordinates returned by the LTA design with the described λ update method to L-curves derived using a range of fixed λ parameters.

Figure 1.

Single-frequency simulations using in vivo $B_1^{+}$ and off-resonance maps. Mean and standard deviation across subjects and slices of (a) flip angle RMSE and (b) integrated RF power, versus number of spokes, for STA design, and LTA designs with and without joint gradient optimization. (c) Representative refocusing patterns illustrating how STA-designed pulses can produce less homogeneous excitations with more spokes. Arrows indicate locations of degraded refocusing with the addition of two spokes to the STA-designed pulse. (d) 90° excitation and 180° refocusing patterns for STA- and LTA-designed pulses at 14 T using simulated field maps for a human head model. Flip angle RMSE values are reported for each pattern.

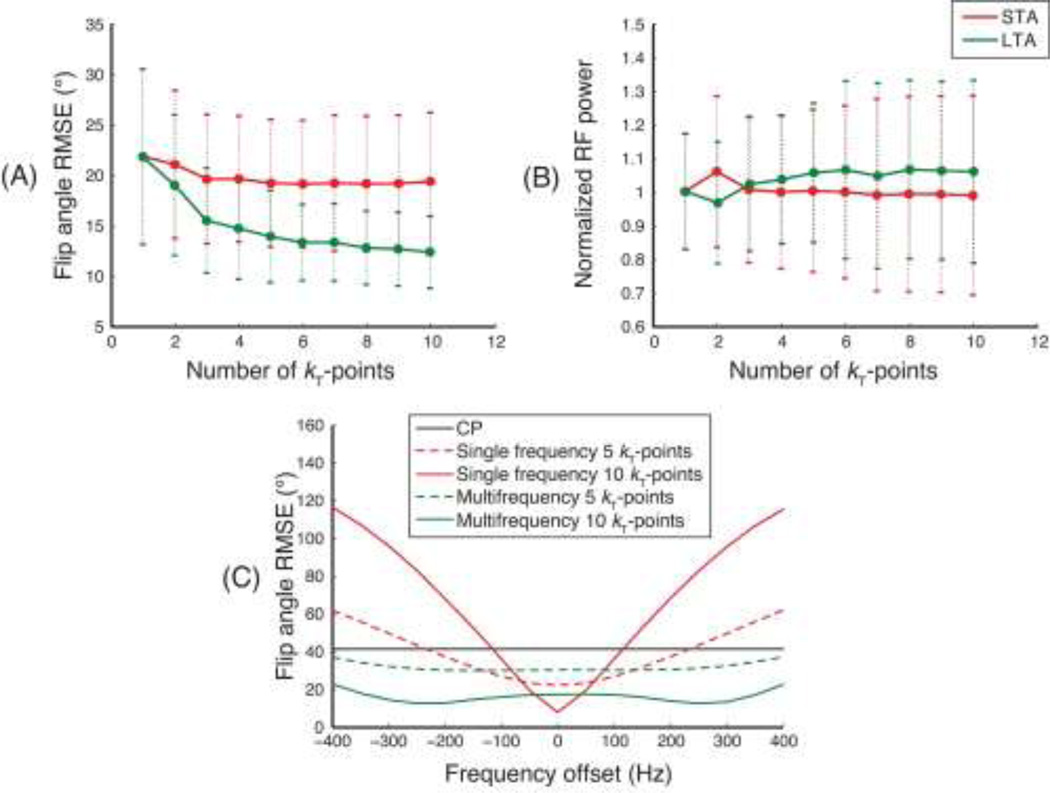
Figure 2 shows the multi-frequency simulation results. The LTA method greatly decreased flip angle total RMSE (Fig. 2a) without significantly increasing RF power (Fig. 2b). The frequency characteristics of different pulse design methods are compared in Fig. 2c. Since a short subpulse duration of 0.1 ms was used, the CP mode pulse had a high but uniform flip angle RMSE across the frequency bands. In comparison, the single-frequency pulses had much lower flip angle RMSE at their target 0 Hz frequency band, but moving off resonance the RMSE degraded to worse than CP mode RMSE. The longer duration of the 10-point single-frequency pulse caused its RMSE to increase more rapidly than the shorter 5-point single-frequency pulse. The multi-frequency pulses showed desired broad band characteristics, with lower overall RMSE than the RF shimming result. Unlike the single-frequency pulses, increasing the number of k_T-points in the multifrequency pulse improved RMSE at all frequencies.

Figure 2.

Multi-frequency k_T-points refocusing simulations using in vivo $B_1^{+}$ and off-resonance maps. Mean and standard deviation across subjects and slices of (a) flip angle RMSE and (b) integrated RF power, versus number of spokes, for STA and LTA designs. (c) Flip angle RMSE as a function of off-resonance frequency, for CP mode, and LTA-designed single- and multi-frequency k_T-points pulses with 5 and 10 spokes.

Experiments

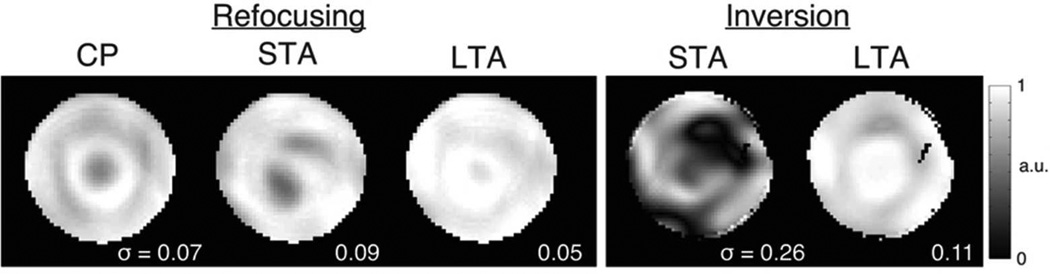
Figure 3 shows the measured refocusing and inversion patterns. In the refocusing case, the LTA-designed k_T-points pulses had the lowest measured refocusing inhomogeneity, with no large refocusing voids. The STA-designed pulses had the highest inhomogeneity. The predicted refocusing patterns had normalized standard deviations of 0.13 (CP), 0.11 (STA), and 0.02 (LTA). In the inversion case, the LTA-designed spokes pulses produced a much more homogeneous inversion than the STA-designed pulses. The predicted inversion patterns had standard deviations of 0.16 (STA) and 0.07 (LTA).

Figure 3.

Single-frequency two-channel 7 T phantom experiment. Measured patterns from (a) 5-k_T-point 180° refocusing pulses and (b) 5-spoke 180° inversion pulses. The patterns are normalized to the maximum amplitude across all three, and the corresponding standard deviations are reported in the corners.

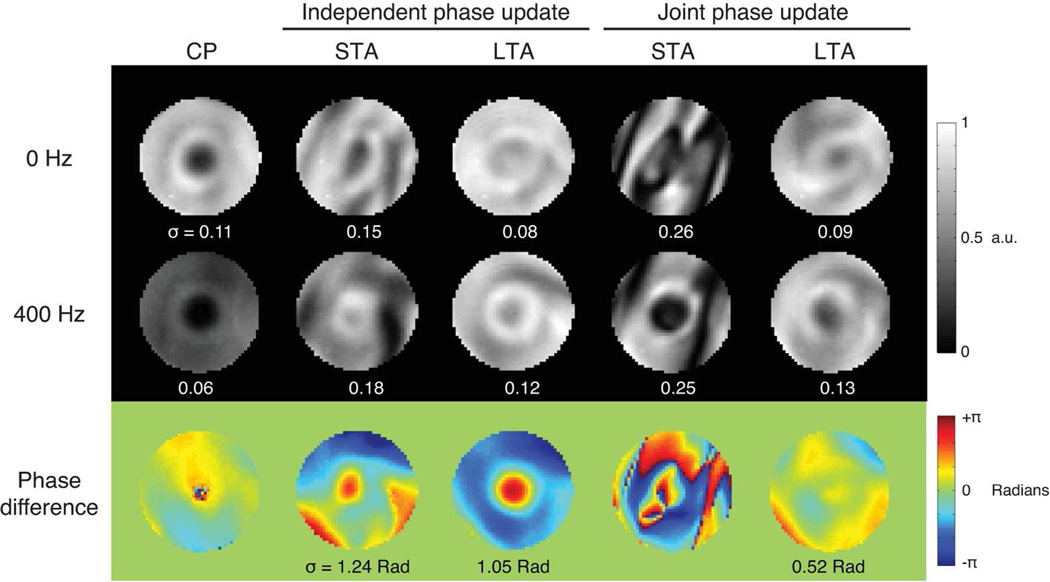
Figure 4 shows the results of the dual-frequency phantom experiment. The STA-designed pulses produced patterns with poorer homogeneity than the CP mode pulses. The LTA design improved on that homogeneity and had the lowest overall standard deviations, with the exception of the 400 Hz CP mode acquisition which had a low standard deviation due to overall lower refocusing efficiency. Pulses designed with the LTA method and independent phase updates showed better homogeneity than pulses designed with joint phase updates, but a significantly more inhomogeneous phase difference pattern.

Figure 4.

Multi-frequency two-channel 7 T phantom experiment. Refocusing patterns (ratios of the SE images and their corresponding GRE images) at 0 and 400 MHz are shown for quadrature circular polarized mode (CP) and 7-k_T-points pulses designed using STA and LTA methods and independent or joint phase updates. The phase difference patterns between the two bands are shown in the bottom row. The standard deviations of the magnitude refocusing patterns and phase difference patterns are reported; they are omitted for the CP and STA joint phase phase patterns due to the many phase wraps in those patterns.

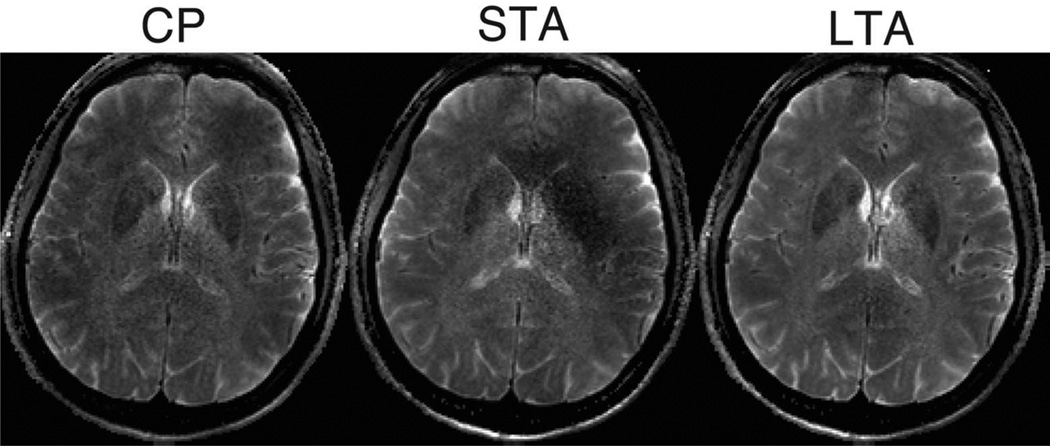
The in vivo SE images are shown in Fig. 5. Compared to the CP-mode excitation, both STA and LTA-designed k_T-points refocusing pulses increased the apparent SNR, but the LTA-designed pulses produced significantly higher signal near the frontal horn of the left lateral ventricle, indicating more complete refocusing there. A map of image intensity modulations due to receive field inhomogeneity was estimated and removed from the images. In addition, a comparison of STA and LTA RF and gradient waveforms is provided in Supporting Figure S2.

Figure 5.

Single-frequency in vivo two-channel 7 T experimental SE images.

Figure 6 shows the fMRI results. In addition to overall more homogeneous image amplitudes, the improved refocusing with the LTA-designed k_T-points pulses resulted in activation maps with a significant increase in spatial sensitivity to the functional region, compared to the CP mode acquisition. There were 143 activated voxels (z > 4.0) for the LTA refocusing compared to 110 for CP mode. Many (n = 53) of the CP mode voxels were spuriously located outside motor cortex; when this was taken into account, the LTA acquisition provided an increase in voxel detection specificity of approximately 150%. CNR (GRE: 2.1; CP mode: 0.74; LTA: 1.13) was also significantly increased (P < 0.05) by an average of 52% in the LTA acquisition compared to the CP mode acquisition. The LTA acquisition voxels were found to more closely co-localize with cortex, whereas GRE activation co-localized additionally with CSF and tissue surrounding large veins, consistent with static refocusing and dynamic averaging of field inhomogeneities within and around large vessels in SE acquisitions [30, 31]. Note the analysis approach presented excludes large veins, resulting in CNR values lower than those reported in some other studies.

Discussion

Simulation and experimental results demonstrated that the proposed magnitude-least squares LTA pulse design algorithm consistently produced pulses with more accurate and homogeneous spokes and k_T-points refocusing and inversion patterns compared to STA-designed and CP-mode pulses. This was seen in both single-frequency and multi-frequency results. To our knowledge, this work (first presented in 2009 [13]) represented the first effort to jointly optimize RF pulses and blipped gradient trajectories at large tip-angles and across multiple resonant frequencies, and the first application of large-tip-angle blipped pulses to fMRI.

The algorithm will form the basis of future work to integrate local and global SAR constraints into LTA spokes and k_T-points designs, which will be necessary to broadly ensure patient safety at ultra high field, particularly with many transmit channels. However, achieving feasible compute times with SAR constraints will require the development of faster RF optimization methods with second-order or near-second-order convergence, such as Newton and quasi-Newton methods [22]. The optimal control search directions used by the present algorithm and others are based on approximate derivatives, which have been shown to spoil the convergence of quasi-Newton methods [32]. Thus, in the future these updates will be replaced with exact derivatives that will require some additional computation but will enable quasi-Newton methods to be used. Since quasi-Newton methods require multiple consecutive iterations to build up an accurate Hessian matrix approximation, the algorithm may be modified so that more RF update iterations are performed for each algorithm iteration, between the gradient and target phase updates that will spoil the approximation and require it to be restarted. Other approaches to reduce peak RF power and SAR include RF amplitude clipping [10] and variable-rate selective excitation [6]. Those methods could also be integrated with the proposed algorithm. Finally, another direction for future research will be to further develop the method for sequences requiring multiple large-tip-angle pulses that should be jointly designed to satisfy required phase relationships, or to enable one pulse to compensate imperfect excitation by another pulse, such as turbo SE imaging or T₂-prepared fast GRE [33].

Conclusion

A magnitude-least squares algorithm was proposed for efficient and accurate design of large-tip-angle parallel transmit RF pulse and blipped gradient waveforms. The algorithm was validated with phantom and human studies, and demonstrated improved SE fMRI at 7T.

Appendix

Calculating the RF Subpulse Weight Search Direction

In this section we provide an expanded description of the algorithm for calculating the RF subpulse weight search direction. The algorithm starts by evaluating Eqs. 13 and 14 for each transmit channel for the last time point in the last subpulse, and the results are substituted into Eq. 12 and accrued into the last N_c entries of Δb. (α^R, β^R) is initialized to (z, 0), corresponding to the last frequency offset rotation in the pulse, and (α^F, β^F) is initialized to the spinor corresponding to all rotations up to the frequency offset rotation preceding the last RF rotation, calculated using Eqs. 1–6. Then the algorithm moves to the next-to-last time point in the last subpulse by updating (α^R, β^R) according to:

$$\left(\begin{array}{c}\hfill {\alpha }^R\hfill \\ \hfill {\beta }^R\hfill \end{array}\right)\leftarrow \left(\begin{array}{cc}\hfill {\alpha }^R\hfill & \hfill -{({\beta }^R)}^{*}\hfill \\ \hfill {\beta }^R\hfill & \hfill {({\alpha }^R)}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill C_{N_t}\hfill & \hfill -S_{N_t}^{*}\hfill \\ \hfill S_{N_t}\hfill & \hfill C_{N_t}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right)$$ [17]

and (α^F, β^F) according to:

$$\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right)\leftarrow \left(\begin{array}{cc}\hfill C_{N_t-1}\hfill & \hfill S_{N_t-1}^{*}\hfill \\ \hfill -S_{N_t-1}\hfill & \hfill C_{N_t-1}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z^{*}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right).$$ [18]

Then Eqs. 13 and 14 are evaluated again for each channel for time point N_t − 1, and the results are again accrued into Δb. The algorithm continues in this way until the beginning of the subpulse is reached. Then it moves to the next-to-last subpulse. When moving from the first time point in the last subpulse to the last time point of the next-to-last subpulse the updates become:

$$\left(\begin{array}{c}\hfill {\alpha }^R\hfill \\ \hfill {\beta }^R\hfill \end{array}\right)\leftarrow \left(\begin{array}{cc}\hfill {\alpha }^R\hfill & \hfill -{({\beta }^R)}^{*}\hfill \\ \hfill {\beta }^R\hfill & \hfill {({\alpha }^R)}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill C_1\hfill & \hfill -S_1^{*}\hfill \\ \hfill S_1\hfill & \hfill C_1\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z_{N_s-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z_{N_s-1}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right)$$ [19]

and:

$$\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right)\leftarrow \left(\begin{array}{cc}\hfill C_{N_t}\hfill & \hfill -S_{N_t}^{*}\hfill \\ \hfill S_{N_t}\hfill & \hfill C_{N_t}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z^{*}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z_{N_s-1}^{*}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z_{N_s-1}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right),$$ [20]

where C_Nt and S_Nt now correspond to the RF rotation parameters of the last time point in the next-to-last subpulse. Then the remainder of the next-to-last subpulse is treated just as the last subpulse was, and the results are accrued into the next-to-last N_c entries of Δb. The algorithm stops when the first time point in the first subpulse is completed. The algorithm can also proceed the opposite direction in time.

Calculating the Gradient Blip Search Direction

In this section we provide an expanded description of the algorithm for calculating the gradient blip search direction. The algorithm starts by calculating the last entry of the search direction vector Δg⃗. (α^R, β^R) is initialized to (A_Ns, B_Ns) (Eq. 3), and (α^F, β^F) is initialized to the product of all RF and gradient rotations up to but not including the last ((N_s − 1)st) gradient blip rotation matrix. Upon evaluating Eqs. 15 and 16 for the last blip and accruing the result into the last entry of Δg⃗, the algorithm moves to the next-to-last blip by updating (α^R, β^R) and (α^F, β^F) as:

$$\left(\begin{array}{c}\hfill {\alpha }^R\hfill \\ \hfill {\beta }^R\hfill \end{array}\right)\leftarrow \left(\begin{array}{cc}\hfill {\alpha }^R\hfill & \hfill -{({\beta }^R)}^{*}\hfill \\ \hfill {\beta }^R\hfill & \hfill {({\alpha }^R)}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill z_{N_s-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z_{N_s-1}^{*}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill A_{N_s-1}\hfill & \hfill -B_{N_s-1}^{*}\hfill \\ \hfill B_{N_s-1}\hfill & \hfill A_{N_s-1}^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right)$$ [21]

and:

$$\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right)\leftarrow \left(\begin{array}{cc}\hfill z_{N_s-2}^{*}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill z_{N_s-2}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill A_{N_s-1}^{*}\hfill & \hfill B_{N_s-1}^{*}\hfill \\ \hfill -B_{N_s-1}\hfill & \hfill A_{N_s-1}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\alpha }^F\hfill \\ \hfill {\beta }^F\hfill \end{array}\right)$$ [22]

and evaluating Eqs. 15 and 16 again for the next-to-last blip. The algorithm continues until Δg⃗ is filled. The algorithm can also proceed the opposite direction in time.