A Century of Enzyme Kinetic Analysis, 1913 to 2013

Abstract

This review traces the history and logical progression of methods for quantitative analysis of enzyme kinetics from the 1913 Michaelis and Menten paper to the application of modern computational methods today. Following a brief review of methods for fitting steady state kinetic data, modern methods are highlighted for fitting full progress curve kinetics based upon numerical integration of rate equations, including a re-analysis of the original Michaelis-Menten full time course kinetic data. Finally, several illustrations of modern transient state kinetic methods of analysis are shown which enable the elucidation of reactions occurring at the active sites of enzymes in order to relate structure and function.

Introduction

In their 1913 paper Leonor Michaelis and Maud Menten sought to achieve “the final aim of kinetic research, namely to obtain knowledge of the nature of the reaction from a study of its progress” (1). The challenge of the day was to account for the full time course of product formation in testing the postulate that the rate of an enzyme-catalyzed reaction was proportional to the concentration of enzyme-substrate complex. They did so without knowing the concentration or even the chemical nature of enzymes—a tribute to the power of quantitative kinetic analysis. Today, the important questions have advanced to asking how enzymes achieve such extraordinary efficiency and specificity, while structural and spectroscopic studies have provided a powerful complement to kinetic analysis to greatly expand our understanding of enzyme catalysis. While the techniques for data collection and analysis have advanced to meet the sophistication of the questions that are being addressed, kinetic analysis has remained as a cornerstone of enzymology because studies of the rate of reaction allow alternative pathways to be distinguished. Here, I will briefly review the methods of kinetic analysis developed by Michaelis and Menten that go beyond the simple initial velocity methods for which they are known, and contrast their analysis with modern computer-based global data fitting methods.

Roger Goody and I recently published a complete translation of the 1913 Michaelis-Menten paper originally written in German (2, 3). We were surprised to learn that Michaelis and Menten performed what can be considered as the first global data analysis of full progress curves, going far beyond the simple steady state kinetic studies for which they are commonly recognized.

As the foundation of their analysis, Michaelis and Menten devised the now popular initial velocity measurements, but they also derived equations for competitive product inhibition and measured the dissociation constant (K_d) for each product. They studied the enzyme, invertase (EC 3.2.1.26, β-D-fructofuranosidase), named for the resulting inversion of optical rotation observed upon conversion of sucrose to glucose plus fructose. Interestingly, the crystal structure of invertase from Saccharomyces was solved for the first time this year (4). Michaelis and Menten chose to study invertase because the change in optical rotation provided a convenient signal to monitor the hydrolysis of sucrose and thereby test the theory that the rate of reaction was proportional to the concentration of the enzyme-substrate complex. They are most noted for the Michaelis-Menten equation, which was first derived by Henri (5), although his experiments failed to support the theory because of shortcomings in his experimental design; namely, the failure to control pH and to account for mutarotation of glucose (1, 2). This provides an important example that is still pertinent today. Testing a scientific theory requires careful measurement and accurate quantitative analysis. Because of their attention to detail in the laboratory and their careful, quantitative analysis, the names of Michaelis and Menten are indelibly linked to the simple equation relating the rate of an enzyme-catalyzed reaction to the concentration of substrate:

$$V=\frac{V_{max}[S]}{K_m+[S]}$$ Eqn 1

Measurement of the binding affinity for an active enzyme-substrate complex was a landmark discovery of the day. Although it is now widely accepted that the Michaelis constant, K_m, is not generally equal to the enzyme-substrate dissociation constant, for invertase the K_m probably is equal to the K_d given the weak apparent binding affinity (16.7 mM). The more general derivation of the Michaelis-Menten equation that is presented in most textbooks is based upon the steady state approximation, as derived 12 years later in 1925 by Briggs and Haldane (6).

Finding a method for fitting the concentration dependence of the initial velocity was problematic for Michaelis and Menten. Estimation of K_m could be obtained from the velocity at half of V_max, but extrapolation to estimate the velocity at infinite substrate concentration presented an obstacle. They devised a complicated analysis based upon the logarithm of the rate and derived an equation analogous to the Henderson-Hasselbalch equation for pH dependence, which was published 4 years later (7). They normalized their data based upon the expected slope of a semi-log plot at the midpoint of the transition, thereby affording an estimation of the rate at infinite substrate concentration and hence, the K_m. It is indeed surprising that in spite of the complexities of this analysis, it was not until twenty years later that Lineweaver and Burk devised the simple reciprocal plot (8). As a tribute to the popularity of this simple algebraic transformation, their paper went on to become the most cited in the history of the Journal of the American Chemical Society.

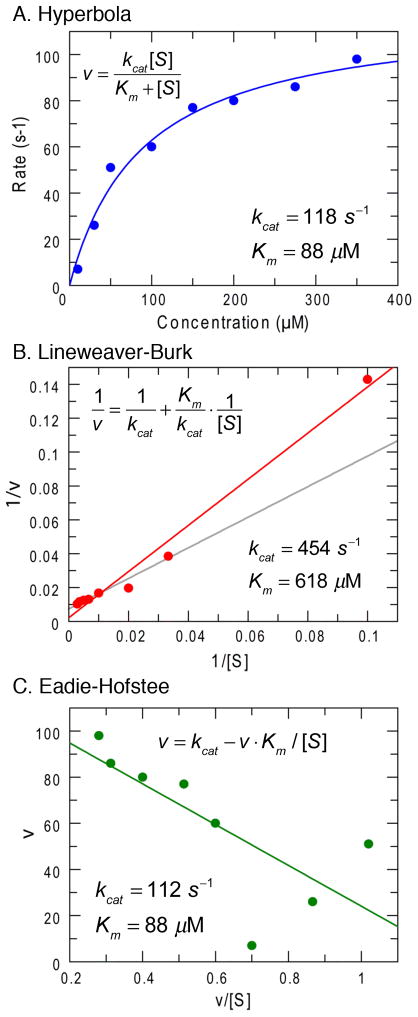
The Lineweaver-Burk reciprocal plot presents some problems due to the unequal weighting of errors as illustrated in Figure 1. Figures 1A, B and C show the same data set fit by nonlinear regression to a hyperbola (Figure 1A) compared to fits derived by linear regression using a Lineweaver-Burk plot (Figure 1B) and an Eadie-Hofstee plot (Figure 1C). In the reciprocal plot, the least accurate data, obtained at the lowest substrate concentrations, alter the slope of the line because of the long lever arm effect on the reciprocal plot, leading to overestimation of k_cat and K_m. Of course, this data set was selected to illustrate the problems and proper weighting of errors based upon the measured standard deviation can rectify the unequal weighting of errors in the reciprocal plot, but that is rarely done. These considerations led to the generation of another transform of the Michaelis-Menten equation, known as the Eadie-Hofstee plot as shown in Figure 1C (9). Arguments have tended to favor the reciprocal plot because it separates the two primary kinetic constants, k_cat/K_m and k_cat as 1/slope and intercept, respectively. Although the Eadie-Hofstee plot produces more reliable estimates (10), the presence of the dependent variable, v, in both axes makes rigorous error analysis difficult. Fortunately, now with the advent of fast personal computers and readily available software for nonlinear regression, these arguments can be relegated to history. Today, there is no reason for fitting data using either linear transformation of the Michaelis-Menten equation in analyzing the concentration dependence of the initial velocity.

Figure 1. Comparison of three methods of fitting data to the Michaelis-Menten equation.

A. Data fit by nonlinear regression to a hyperbola. B. Data fit to a Lineweaver-Burk reciprocal plot. The gray line shows the fit obtained after omitting the point at the lowest substrate concentration. C. Data fit using the Eadie-Hofstee equation. In each figure, the equation and the resulting k_cat and K_m values are displayed.

Michaelis-Menten Progress Curve Analysis

Although largely forgotten in the past century, Michaelis and Menten were the first to fit full time course kinetic data and compute a fitted parameter by averaging over all of the data to provide a kind of global analysis. They derived an equation that predicted a constant term that could be calculated from the product formed at each time point as the reaction progressed toward completion, including data obtained at several starting sucrose concentrations and accounting for product inhibition.

$$\frac{1}{t}·\left(\frac{1}{S_0}+\frac{1}{K_F}+\frac{1}{K_G}\right)·S_0·ln\frac{S_0}{S_0-P}+\frac{1}{t}·\left(\frac{1}{K_S}+\frac{1}{K_F}+\frac{1}{K_G}\right)·x=\mathit{const}$$ Eqn 2

where S₀ is the starting concentration of sucrose, t is time, P is the time-dependent concentration of product (fructose or glucose), and K_S, K_F and K_G are the dissociation constants for sucrose, fructose and glucose, respectively. This analysis required prior estimates for each of the dissociation constants derived from initial velocity measurements. The rigorous test of their model was based upon calculating the value of this constant for each data point and then examining whether there were any systematic deviations of the value of the constant as a function of starting substrate concentration or time of reaction. They stated, “The value of the constant is very similar in all experiments and despite small variation shows no tendency for systematic deviation neither with time nor with sugar concentration, so that we can conclude that the value is reliably constant.” The average value of this constant then represents a kind of global data fitting since it was calculated from fitting all of the data. Interestingly, the constant they derived was V_max/K_m, not the Michaelis constant.

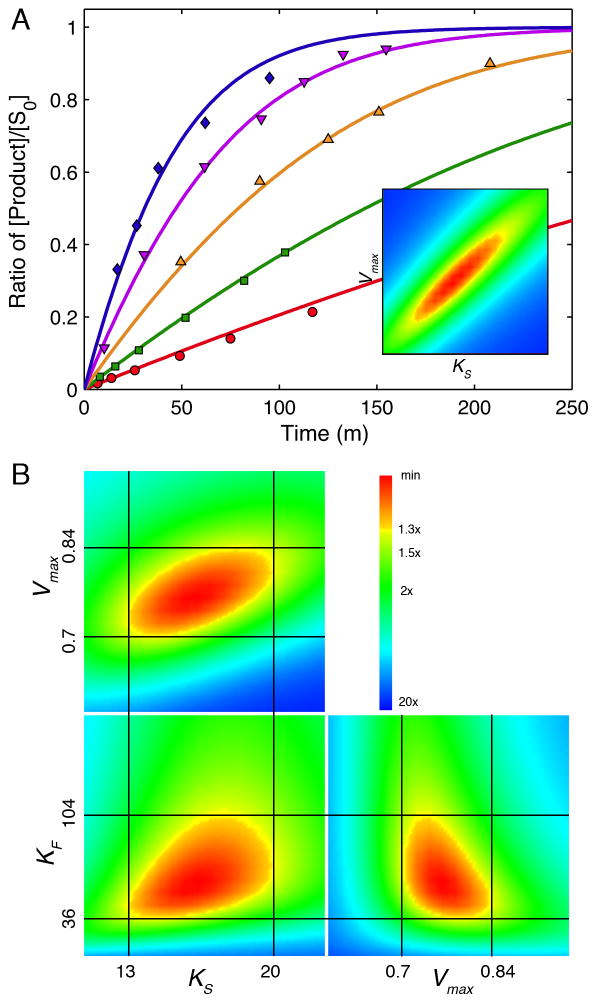
It is quite satisfying to note that modern computational methods of data fitting produce essentially the same value for V_max/K_m as that derived by Michaelis and Menten with pen and paper 100 years ago. Michaelis and Menten presented an average value of V_max/K_m = 0.045 ± 0.003 m⁻¹, whereas our global analysis of their data gives a value of 0.046 ± 0.001 m⁻¹. Figure 2A shows the original Michaelis-Menten full progress curve data fit by nonlinear regression analysis based upon numerical integration of rate equations for the complete model (Scheme 1) along with confidence contour analysis using KinTek Explorer software (11, 12). An example file (Michaelis-Menten_1913.mec) showing these data is available with the free student version of KinTek Explorer available for both Mac and Windows PCs at www.kintek-corp.com.

Figure 2. Global analysis of Michaelis-Menten 1913 data.

A: the original Michaelis-Menten data are shown with the results of global fitting. The ratio of product formed (fructose or glucose ) divided by the starting substrate concentration is shown as a function of time for various starting sucrose concentrations (20.8, 41.6, 83, 167 and 333 mM). The smooth lines are drawn based on numerical integration of rate equations derived from Scheme 1 using the rate constants summarized in Table 1 and an enzyme concentration of 25 nM. The Inset shows the confidence contours for a fit involving only two variables to define V_max and K_S. B: Confidence contour analysis showing the dependence of χ² on each pair-wise combination of three constants (K_S, V_max, and K_F, defined by k₋₁, k₊₂ and k₊₅ respectively, according to Scheme 1). The index for the color coded display of χ² values relative to the minimum are given by the inset. The central red area defines parameters yielding an acceptable fit. Upper and lower error limits for each parameter are obtained from a threshold defined by a 1.3-fold increase in χ² over the minimum (11), and are designated by the thin black lines and the values listed on each axis.

Scheme 1.

During the past century, fitting full time course kinetic data has not gained the wide acceptance of initial velocity measurements, in part, because there is no universal equation describing the approach to equilibrium. Derivations usually rely upon the approximation that the substrate remains in excess over enzyme even as the reaction approaches equilibrium, a requirement that may not always be met. New approaches to deriving an analytical expression for full time course kinetics have been presented (13), but even these require complex mathematical functions. Recently there has been increased interest in fitting full time course kinetic data brought on by the ease of fitting based upon numerical integration of rate equations without simplifying approximations (12, 14, 15). Indeed, as shown in Figure 2A, global fitting of the original Michaelis-Menten data easily reproduces in seconds what must have taken months of computation by hand. It is a tribute to their skill and diligence that modern computer based analysis provides essentially the same value for their constant as Michaelis and Menten calculated a century ago.

Fitting Data based on Computer Simulation

In the traditional data fitting protocol, a model is proposed and equations are derived to account for the time dependence of the reaction. One then derives another equation to fit the substrate concentration dependence of the fitted parameters to extract primary kinetic constants. For example, in the case of steady state kinetic data, the time dependence is fit to a straight line, based upon the steady-state approximation. The rate is then plotted as a function of substrate concentration and fit to a hyperbola to derive estimates of k_cat and K_m. To study the effect of an inhibitor, the whole process is repeated and then the apparent k_cat and K_m values are plotted against the inhibitor concentration to ultimately derive estimates of the true k_cat and K_m values and K_I for the inhibitor. Accordingly, one can describe this process as a kind of parsing of the kinetic data to separate the complex terms to ultimately derive the primary kinetic parameters. Proper error analysis requires propagation of measurement errors through each step of analysis.

Data fitting based upon computer simulation represents a major paradigm shift requiring new insights. Data are fit to a chosen model using numerical integration of the rate equations so that no approximations or simplifying assumptions are required (12, 15). Moreover, in the process of finding an optimal fit, the intrinsic rate constants are varied in seeking a function that mimics the time course of the reaction. Thus, the rate constants are derived directly, not indirectly through complex functions of rate constants. Like other regression analysis, the best fit base upon seeking a minimum χ² value (16):

$${\chi }^2=\sum _{i=0}^{N-1}{\left(\frac{y_i-y(t_i)}{{\sigma }_i}\right)}^2$$ Eqn 3

where y_i represents the data as a vector of N points, y(t_i) is the computed value at time t_i, and σ_i (sigma) is the standard deviation of the measurement. If sigma is not known, it generally is assumed to be identical for all data or set to unity. An optimal fit is derived by analysis of successive trials to converge on a best fit defined by a minimum χ². However, in fitting based upon simulation, the y(t_i) values are computed by numerical integration of the rate equations rather than from a defined equation.

Fitting to derive rate constants directly based upon a model bypasses the need to subsequently fit the concentration dependence of the measured rate after fitting the primary kinetic data to a simplified function. This represents a major paradigm shift in the way in which we design and interpret experiments. For example, rather than conducting a series of measurements restricted to the first 10–20% of reaction at various substrate concentrations, one can monitor a single reaction allowing the reaction to run to completion, which provides data sufficient to define k_cat and K_m if there is no product inhibition. As described in more detail below, the full time course contains within it the concentration dependence of the reaction rate as the substrate is consumed over time.

Fitting the original Michaelis-Menten data by computer simulation illustrates the methods involved. First we enter the complete model as given in Scheme 1. We then enter starting concentrations of enzyme and sucrose. The enzyme concentration was not known by Michaelis and Menten, but we can estimate an enzyme concentration of 25 nM in their assays based on modern estimates of k_cat = 500 s⁻¹ (4) and the V_max value reported by Michaelis and Menten (0.75 m⁻¹). Although the simulation requires an enzyme concentration, any arbitrarily small enzyme concentration would suffice, and it is only used in our analysis to convert k_cat/K_m to V_max/K_m values for comparison with the Michaelis-Menten analysis. Nonetheless, this estimate provides anecdotal insight into how the original experiments may have been performed.

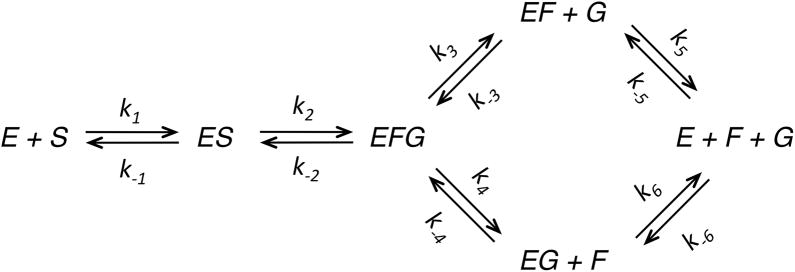
The complete model requires values for 12 rate constants, which far exceeds the information content of the data. One could allow all 12 rate constants to vary in fitting and then use a complete expression for calculation of k_cat and K_m values, but the apparent errors on the rate constants would be large because there are multiple sets of parameters that could account for the data. Therefore this approach would not allow estimation of errors on k_cat and K_m. A given set of kinetic data will only suffice to define a limited number of kinetic parameters. Thus, in order to obtain accurate error estimates, modeling based upon numerical integration of rate equations requires some rate constants to be fixed at arbitrary values to reduce the number of variables. For example for a simple enzyme-catalyzed reaction, one can use either of the following scenarios to obtain estimates of k_cat and K_m.

$$\begin{array}{l}\text{Case}1:E+S\underset{(0)}{\overset{k_1}{\rightleftarrows }}ES\underset{(0)}{\overset{k_2}{\rightleftarrows }}EP\underset{(0)}{\overset{(k_3\gg k_2)}{\rightleftarrows }}E+P;k_{\mathit{cat}}/K_m=k_1;k_{\mathit{cat}}=k_2\\ \text{Case}2:E+S\underset{(k_{-1}\gg k_2)}{\overset{k_1}{\rightleftarrows }}ES\underset{(0)}{\overset{k_2}{\rightleftarrows }}EP\underset{(0)}{\overset{(k_3\gg k_2)}{\rightleftarrows }}E+P;K_m=k_{-1}/k_1;k_{\mathit{cat}}=k_2\\ \text{Case}3:E+S\underset{k_{-1}}{\overset{(k_{\mathit{diffusion}})}{\rightleftarrows }}ES\underset{(0)}{\overset{k_2}{\rightleftarrows }}EP\underset{(0)}{\overset{(k_3\gg k_2)}{\rightleftarrows }}E+P;K_m=k_{-1}/k_1;k_{\mathit{cat}}=k_2\end{array}$$

In each case, the rate constants in parentheses are held fixed at the designated values so that there are only two variable parameters during the data fitting. In Case 1, we use irreversible binding and chemistry to directly estimate k_cat/K_m = k₁ and k_cat = k₂. This method has the advantage of establishing the specificity constant directly and is preferred if there are large errors in estimating k_cat and K_m, for example if the K_m is larger than the highest substrate concentration achievable experimentally. However, Case 1 cannot be used if the reaction is fully reversible. Cases 2 and 3 both represent a rapid equilibrium binding assumption for calculating K_m, but with either k₁ or k₋₁ fixed so that only one parameter is varied in computing K_m = k₋₁/k₁. Case 3 has the advantage in that it guards against modeling with second order rate constants exceeding the theoretical diffusion limit of approximately 10⁹ M⁻¹s⁻¹. Of course, the actual mechanism may not involve a rapid equilibrium binding, but since the steady state measurements are not able to define the individual rate constants, either of these methods can be used to calculate k_cat and K_m. As long as appropriate equations are used to calculate k_cat and K_m values, the values chosen for the fixed constants do not affect the outcome of the calculation, and it is easy to show that multiple fits using various combinations of parameters all produce the same k_cat and K_m values. This analysis quickly illustrates that the information content of steady state kinetic data, whether based on initial velocity or full progress curve kinetic measurements, is only sufficient to derive two parameters, k_cat and K_m (or k_cat/K_m). However, if the reaction is reversible, or if there is significant product inhibition, then the data can provide additional information to define one or two additional parameters; namely, k_cat and K_m values for the reverse reaction (from k₋₃ and k₋₂) as described in detail below.

A common misconception is that it is better to fit steady state data by traditional initial velocity methods to derive estimates for k_cat and K_m because fitting by simulation is model-dependent and therefore the parameters will be invalid if the model is incorrect. However, one should note that derivation of the equations for steady state kinetic parameters is also based upon a model, albeit a simple one. In fitting by simulation, one can derive estimates for k_cat and K_m from any minimal model that adequately accounts for the data while satisfying criteria for goodness of fit. One could always use a more complex model and the resulting k_cat and K_m values would be the same in either case, independent of the model chosen. Like two sides of the same coin, since steady state kinetics cannot distinguish alternative models, any model providing a good fit is sufficient for computing k_cat and K_m values.

Michaelis and Menten noted significant product inhibition and estimated the dissociation constants for both fructose and glucose based upon competitive inhibition of the initial velocity. In fact, the full time course kinetic data published by Michaelis and Menten cannot be adequately fit without including product inhibition (2). To fit the Michaelis-Menten data, we can assume rapid equilibrium binding of sucrose, irreversible chemistry, and fast, but reversible product release to account for product inhibition. Accordingly, we can directly calculate k_cat = k₂, K_S = k₋₁/k₁ and K_P = k₃/k₋₃. The “global fit” based upon Equation 2 only allowed Michaelis and Menten to test the ability of their model to account for the full progress curves using their prior estimates of K_d values for sucrose, fructose and glucose, but they could not use their analysis of full time course kinetics to obtain independent estimates of K_S, K_F and K_G. However, fitting the same data set by simulation affords estimates of K_m and V_max/K_m and an average K_d for product inhibition. Michaelis and Menten suggested that the ternary E.F.G complex did not accumulate to a significant extent based upon the weak binding of glucose and fructose. Therefore to simplify the modeling of the kinetics, we employ a fast, irreversible release of the first product from the E.F.G complex. Accordingly, we can model the data using Scheme 1 and the rate constants summarized in Table 1. Again, it is important to emphasize that the intrinsic rate constants need not be correct since they are unknown; rather, they are only used to calculate the steady state kinetic parameters that are defined by the data.

Table 1.

Invertase kinetic parameters^a

Rate constant	Value	Parameter
k1	(1e+06 mM−1m−1)	KS = 16.5 mM
k−1	1.65e+07 m−1
k2	30600 m−1	Vmax = k2[E]0
k−2	(0)	= 0.76 mM/m
k3	(5e+07 m−1)	Assumed fast, irreversible product release
k−3	(0)
k4	(5e+07 m−1)
k−4	(0)
k5	5.88e+07 m−1	KF = 58.8 mM
k−5	(1e+06 mM−1m−1)
k6	9.1e+07 m−1	KG = 91 mM
k−6	(1e+06 mM−1m−1)

^aKinetic parameters used to model the original Michaelis-Menten data are summarized. Modeling was based upon a nominal enzyme concentration of 25 nM, in order to mimic the V_max/K_S value of 0.045 m⁻¹ reported by Michaelis and Menten (1–3) and the recent estimate of k_cat = 500 s⁻¹ (4). The values reported here for k₋₁ and k₂ were derived by global fitting using KinTek Explorer and gave V_max/K_S = 0.046 m⁻¹. Values in parentheses were held constant during fitting. The values of k₅ and k₆ were held in a constant ratio of k₆/k₅ = 1.55.

Globally fitting the original Michaelis-Menten data using computer simulation affords values for K_m and V_max/K_m comparable to the values derived by Michaelis and Menten (2). It is interesting extend this analysis to ask whether the full time course data are also sufficient to define product dissociation constants, K_F and K_G. First, one must note that fructose and glucose are produced in equal quantities during the reaction; therefore, there can be no information in the data to distinguish the two. Accordingly, the only reasonable questions to ask are whether the data are sufficient to define an average dissociation constant, or whether one could derive reasonable estimates of the two constants if the ratio of their two values were known. Using the latter approach, we fit the data globally keeping K_F/K_G = 1.53, based upon the measurements of Michaelis and Menten. We fit the data set globally to derive three constants, k_cat, K_m and K_F to get the results shown in Figure 2A.

Confidence contour analysis

Using computer simulation it is simply too easy to employ an overly complex model, and indeed, as described above the method requires a complete model with more unknowns than can be defined by the data in many cases. Therefore, a significant challenge in data fitting is to avoid over-interpretation by understanding the inherent information content of a given set of data and adjusting the model or restricting the range of fitted parameters accordingly. This problem is evidenced by attempts to extract free energy profiles involving eight rate constants from full time course kinetic data on alanine racemase (17), when the data are only sufficient to define k_cat and K_m values in forward and reverse directions (11). Thus, one must have a firm grasp of the information content of the kinetic data in order to derive fits based upon a minimal model and a well-constrained set of rate constants. Moreover, one needs tools to assess the extent to which kinetic parameters are defined by the data. To this end, we added confidence contour analysis to the KinTek Explorer software, where one rate constant at a time is varied systematically and the data are then fit, allowing all other variable parameters to be adjusted in seeking the minimal χ² value. Examining the variation in χ² as a function of each variable then provides a realistic assessment of the extent to which the data constrain each parameter, independent of the values of all other fitted parameters. This is fundamentally different from typical nonlinear regression covariance analysis, which is based upon analysis of the variation in χ² for each parameter at the best fit values of all other parameters. Accordingly, typical standard error values derived from nonlinear regression grossly underestimate the error range of each parameter when the parameters are seriously under-constrained and/or they are correlated by nonlinear functions (11).

It is important to note that evaluation of the quality of a given data fit is composed of two parts. First, goodness of fit can be evaluated based upon visual inspection to ensure that the fitted curve tracks the centerline of the scatter in the data without systematic deviations. Although this “chi by eye” is somewhat subjective, it provides a good indication as to whether the model is adequate to account for the data and a trained eye can discover systematic deviations better than any algorithm. If the standard deviation (sigma) of the original data is known, goodness-of-fit can be quantitatively evaluated based upon the expectation that χ², when normalized by the known sigma values as in Equation 3, should equal the degrees of freedom, defined as the number of data points minus the number of independent variables (18). Once a good fit is achieved, the second and equally important part of evaluating a data fit is to determine whether the parameters are well constrained by the data. An overly complex model can provide a good fit, but with ill-defined extraneous parameters. Confidence contour analysis addresses the extent to which parameters are defined by the data once a good fit is achieved.

Results of two-dimensional confidence contour analysis of the Michaelis-Menten data are shown in Figure 2B, demonstrating that estimates for three kinetic parameters can be derived from these data by global fitting. Each pair-wise combination of parameters produces a well-defined local minimum in χ² as evidenced by the areas shown in red. There are two methods of estimating errors on parameters. First nonlinear regression analysis returns a standard error, which can be reliable if the parameters are well constrained, but can be grossly misleading if they are not (11). Secondly, we can use a set threshold increase in χ² to set upper and lower confidence limits on each parameter, which has the advantage of allowing for asymmetric error limits; for example, in some cases, data may define a lower limit on a given rate constant, but no upper limit. The set threshold is calculated based upon the number of data points and number of fitted parameters (11). In this case, a threshold of 1.3x the minimum χ² value is appropriate. From the analysis shown in Figure 2, K_S ranges from 13 to 20 mM (16.5 ± 3 mM), which agrees with the estimate of 16.7 mM reported by Michaelis and Menten. The value for K_F (calculated from k₅/k₋₅) shows a wider margin of error (58.8 ± 20, upper and lower limits of 36 and 104 mM) indicating the data are not sufficient to define this value with precision, but do afford a reasonable estimate. Data collected at longer times or after the addition of product at the start of the reaction would have provided a more refined value. Indeed, the values for K_S and K_F reported by Michaelis and Menten were based upon much more data than contained in Figure 2A.

We obtained a value of V_max = 0.76 ± 0.06 mM/m (upper and lower limits of 0.7 and 0.84 mM/m). To get error estimates on V_max/K_m, one could propagate error estimates on V_max and K_m to compute the ratio, V_max/K_m = 0.046 ± 0.008 m⁻¹. However, the apparent second order rate constant, V_max/K_m is known with greater certainty than either V_max or K_m individually, as indicated by the oblong shape of the confidence contour in the inset to Figure 2A. Thus to get error estimates on V_max/K_m directly, one needs to restrict the fitting to a single parameter defining V_max/K_m. Applying this analysis to the data in Figure 2A provides V_max/K_m = 0.046 ± 0.001 m⁻¹, which compares remarkably well with the value of 0.045 ± 0.003 m⁻¹ reported by Michaelis and Menten. In addition, our analysis shows that this limited data set was sufficient to provide estimates for each of the three kinetic parameters based upon global data fitting (V_max/K_m, K_S and K_F), although additional data would have allowed resolution of the dissociation constants for each product and increased the precision of each estimate.

Understanding the information content of full time course kinetic data

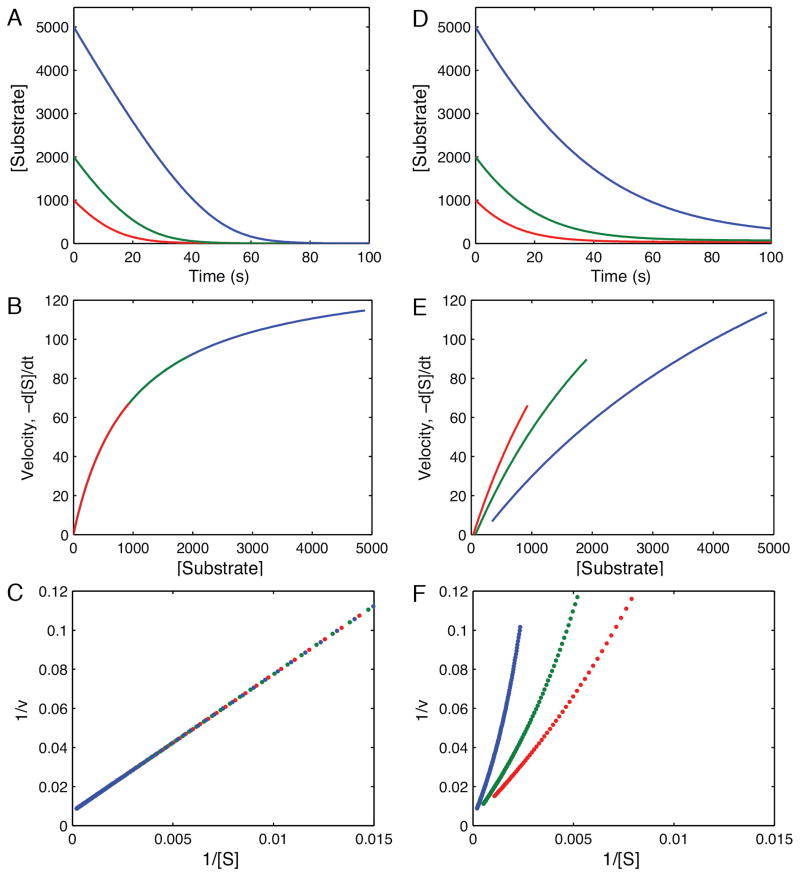
Figure 3 illustrates an approach toward understanding full progress curve kinetics, taking advantage of the utility of the simulation software to generate synthetic data. First, we show a graphical deconvolution of the full time course kinetic data to develop an understanding of the method and the information content of the data. Figure 3A shows the simulation of the kinetics of substrate depletion for an irreversible reaction, using Scheme 2 and rate constants summarized in Table 2. The data illustrate the decrease in rate as the substrate is depleted and the reaction approaches the endpoint. The instantaneous rate, obtained as the negative of the slope (-d[S]/dt) at each time point can be plotted as a function of the remaining substrate concentration, revealing a hyperbolic relationship (Figure 3B). Graphing of the rate versus concentration on a Lineweaver-Burke plot demonstrates the linear relationship in the reciprocal plot (Figure 3C). Since the data can be reduced to a straight line, it is clear that the information content of the data can be represented sufficiently by only two parameters, k_cat and K_m. Thus, there is nothing magical about full progress curves, and they represent essentially steady state information because they are based upon multiple enzyme turnovers.

Figure 3. Simulation and deconvolution of progress curves.

A. Progress curves calculated at three starting substrate concentrations (5000, 3000 and 1000 μM) for a simple irreversible enzyme catalyzed reaction (Scheme 2) and showing the decrease in substrate concentration over time. B. The first derivative was calculated from the slope at each time in A, and plotted as a function of the remaining substrate concentration in B, where the data fit a hyperbola. C. The data shown in B are graphed as a Lineweaver-Burke plot, showing a straight line dependence, and demonstrating reduction of the data to a function of only two parameters. D. A set of progress curves for a fully reversible enzyme-catalyzed reaction. E. Analysis of the instantaneous rate as a function of remaining substrate concentration from D shows deviation from a simple hyperbolic relationship. F. Attempts analyze the substrate concentration dependence of the rate on a Lineweaver-Burke plot show deviations from linearity. Simulations were performed using the rate constants summarized in Table 2 according to Scheme 2 and an enzyme concentration of 1 μM.

Scheme 2.

Table 2.

Kinetic parameters used for synthetic full time course kinetics^a

Rate constant	Figure 2A, 3A	Figure 2D, 3C
k1	10 μM−1s−1	10 μM−1s−1
k−1	(10000 s−1)	(10000 s−1)
k2	140 s−1	140 s−1
k−2	0 s−1	10 s−1
k3	(10000 s−1)	(10000 s−1)
k−3	0 s−1	5 s−1

^aThe rate constants used to generate synthetic data according to Scheme 2 and shown in Figures 2A, 3A, 2D, and 3C are summarized. Normally distributed random noise was added to the synthetic data (sigma = 50, 1% of the maximum signal). Values in parentheses were held fixed in subsequent data fitting.

Figures 3D–F show the same analysis for an enzyme where the reaction is readily reversible. In this case, as the substrate is depleted, product builds up and rebinds to the enzyme, leading to product inhibition and reversal of chemistry. Attempts to transform the data by analysis of the rate as a function of concentration (Figure 3E) and on a Lineweaver-Burke plot (Figure 3F), show that the data can no longer be represented by two parameters. More complex modeling is required. Indeed, fitting the data by nonlinear regression based upon numerical integration of rate equations for a fully reversible model affords resolution of four rate constants sufficient to define k_cat and K_m in each direction. The important question is to ask whether each of the rate constants is well constrained in fitting the synthetic data. Keeping in mind that these are synthetic data generated with a relatively small standard deviation and a normal distribution of errors, this test represents the best possible scenario for defining the information content of kinetic data. Accordingly, this protocol of generating synthetic data with a standard deviation that mimics experimental data provides a standard for defining the maximum number of parameters that could be obtained from a given experiment.

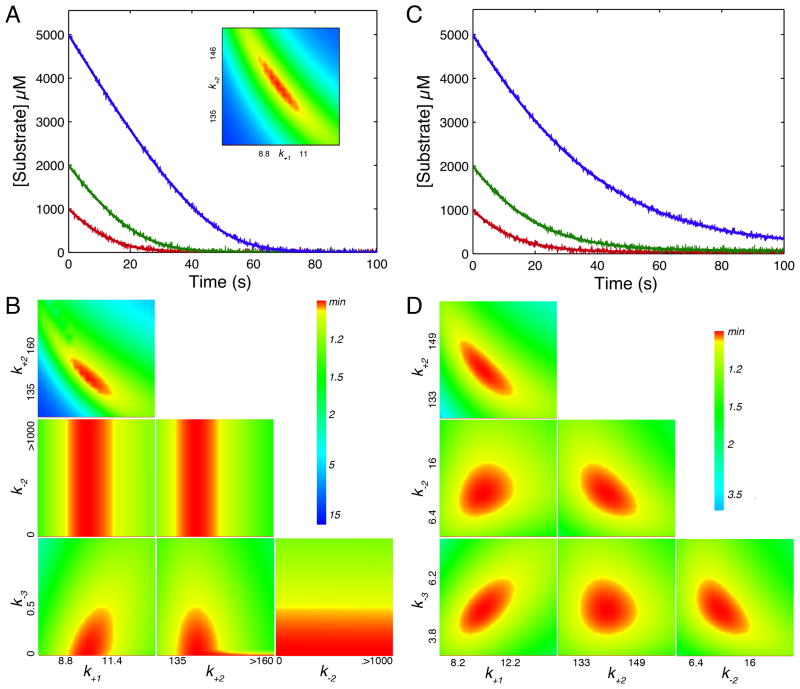
Synthetic data were generated using both an irreversible kinetic model (Figure 4A) and one where chemistry and product dissociation are readily reversible (Figure 4C) according to the rate constants listed in Table 2. Figure 4B shows the confidence contour analysis resulting from an attempt to fit four constants to the irreversible kinetic data set. It is apparent that k₊₁ (defining K_m = k₋₁/k₊₁) and k₂ (defining k_cat) are well constrained. However, k₋₂ and k₋₃ are not well defined. Interestingly, although there is no lower limit, there is an upper limit on k₋₃ (the rate of product rebinding) leading to the conclusion that the K_d for product binding must be greater than 20 mM (k₃/k₋₃ = 10000/0.5). This is based upon the observation that there was no detectable deviation in the shape of the curves that might have indicated product inhibition, and accordingly it sets a lower limit on the magnitude of the K_d for product. Also note that there is no upper limit on the magnitude of k₋₂ over the range of the search, but this is dependent on the value chosen for k₃ (10,000 s⁻¹). As shown in the inset to Figure 4A, when only two constants are allowed to vary (k₋₂ and k₋₃ are held fixed at zero), the confidence contour shows that k₁ (K_m) and k₂ (k_cat) are well constrained. Moreover, the long shape of the range of acceptable fits (red area) indicate that the product k₁*k₂ (defining k_cat/K_m = k₁k₂/k₋₁) is better defined than either individual parameter.

Figure 4. Understanding progress curve kinetics.

A. Synthetic data were generated according to Scheme 2 using the rate constants in Table 2 for an irreversible model. The data were then fit by nonlinear regression to the model with four variable rate constants to get the confidence contours shown in B. The inset to figure A shows the confidence contour obtained with only two variable parameters. C. Synthetic data were generated using the rate constants in Table 2 for a fully reversible model and then fit to generate the confidence contours shown in D. All synthetic data were generated with random error following a normal distribution with a sigma value of 50 (1% of the maximum signal), and using an enzyme concentration of 1 μM. The axes labels on the confidence contour plots show the upper and lower limits for each rate constant defined by a 1.05 threshold in χ² as described (11). All computations were performed using KinTek Explorer (12).

In the case of a reversible reaction as shown in Figures 4C–D the identical experiment provided well constrained estimates for four kinetic parameters, thereby defining k_cat and K_m in both the forward and reverse directions. Thus, when the reverse rate constants (k₋₂ and k₋₃) are significant relative to the forward rate constants, the shape of full time course curves are perturbed sufficiently for the values of the reverse kinetic parameters to be derived from the data. This analysis demonstrates that the same experiment, performed under identical conditions can yield 2, 3 or 4 kinetic parameters, depending on the relative magnitudes of the underlying rate constants. Accordingly, comprehensive global data fitting is essential for evaluating the information content of the data and the confidence contour analysis provides an important check to establish upper and lower limits for each constant. If we had attempted to fit the data in Figure 4C using a model with all 6 rate constants (not shown), the confidence contour analysis would have revealed the expected limits; namely, that k₁ ≥ k_cat/K_m, k₂, k₃ ≥ k_cat for the forward reaction and k-3 ≥ (k_cat/K_m)_rev and k₋₂, k₋₁ ≥ k_cat,rev for the reverse reaction. Although confidence contour patterns can be somewhat complex, they reveal accurate details regarding the contributions of individual rate constants to the measurable k_cat and K_m values and the information content of the data. They provide a clear visual indicator when parameters are well constrained, and even when a given parameter is not well constrained, the confidence contour analysis accurately reveals upper or lower limits that are important mechanistically.

Beyond the Steady-State

For the past century, the analysis of enzyme kinetics has been dominated by the use of initial velocity measurements because of the practical simplicity of the methods. Large volumes have been published full of equations for different enzyme pathways, providing boilerplates for kinetic analysis to establish the orders of substrate binding and product release (19, 20), although some texts also include a brief introduction to transient-state kinetics (21). Emphasis has often been placed on measurement of the Michaelis constant, K_m, because it can be measured without knowing the enzyme concentration, as was the case for Michaelis and Menten, and can be obtained even without knowing the absolute rate of reaction. Although most enzymologists acknowledge that the K_m is not necessarily equal to the substrate dissociation constant, the undercurrent of that thought still permeates the interpretation of kinetic data today.

Modern enzymology is focused on understanding the structure/function relationships governing catalysis. Based upon structures derived by x-ray crystallography or NMR, models are proposed for how the substrate binds at the active site, what residues come into contact with the substrate(s) and how they bring about a chemical transformation and finally release products. The focus is on the events following substrate binding and preceding product release, and accordingly, steady state kinetic studies to establish the order of substrate binding and the order of product release are of minimal utility. To address the pertinent questions of today, we must go beyond the steady state to observe reactions occurring at the enzymes’ active sites. Accordingly, modern kinetic analysis requires the application of fast kinetic methods sufficient to resolve events on the time scale of a single enzyme cycle, and demands rigorous, quantitative data analysis to interpret those results in a manner consistent with steady state turnover.

The methods of analysis and equations governing presteady state kinetics have been reviewed previously (22, 23). Analytical integration of rate equations yields a sum of exponential terms with one exponential for each kinetically significant step in the pathway:

$$y=c+\sum _{i=1}^n{A}_i·\mathit{exp}(-{\lambda }_i·t)$$

where c is the endpoint of the reaction with n exponential terms, each with a defined rate (λ_i) and amplitude (A_i). For a one-step reaction, the observed rate of the exponential decay (λ) is the sum of the forward and reverse rate constants. For a two-step reaction, the two exponential decay rates are the roots of a quadratic equation, while for a three-step reaction, the three exponential terms are the roots of a cubic equation, and so on. Thus the math soon becomes intractable for any realistic model. Moreover, fitting kinetic data to multiple exponentials is error prone because of the arbitrary rates and amplitudes. In reality, rates and amplitudes are related and this interdependence is lost when fitting to sums of exponentials. After fitting the primary data, one still has to analyze the concentration dependence of the observed rates and amplitudes in attempting to extract the underlying intrinsic rate constants. Thus, the fitting of transient state kinetic data is best accomplished by global data fitting, relying on fast computers to do numerical integration of rate equations to simulate each experiment where the primary fitted parameters extracted from the data are the rate constants. Moreover, multiple experiments can be fitted simultaneously in order to obtain a single comprehensive model that accounts for all of the data (12, 24). Thus modern computational methods bypass the difficult, often impossible step of deriving equations for fitting data and avoid the requisite simplification of complex reaction schemes, thereby affording a comprehensive analysis without simplifying approximations. It is also important to note that fitting based upon simulation uses information derived from both the rate and the amplitude of the observed reactions.

Information content of steady-state and transient-state kinetic data

In order to illustrate the typical evolving information as research progresses, three experiments were simulated to generate synthetic data for a simple enzyme catalyzed reaction according to Scheme 2 and the rate constants given in Table 3 (last row). For each of the three experiments, conventional fitting will be described revealing the information content of the data and the patterns indicative of the underlying mechanism. Then the results of global fitting will be shown, with each experiment contributing additional information to the growing body of knowledge.

Table 3.

Experimental information content: Kinetic parameters derived from global fitting^a

Experiment	k1 (μM−1s−1)	k−1 (s−1)	k2 (s−1)	k−2 (s−1)	k3 (s−1)	k−3 (μM−1s−1)
A	≥ 2.6		≥ 6.3		≥ 6.3
A-Bb	2.6 ± 0.01	(0)	≥ 500c	≥ 260c	9.7 ±0.4	< 0.1
A-Bb	≥ 20c	≥ 220c	88 ± 1.4	15.6 ± 1	7.9 ±0.06	< 0.1
A-B-C	55 ± 2	580 ± 20	83 ± 0.5	14.6 ± 0.3	8.0 ±0.03	0.09 ± 0.01
Simulated	57.2	600	82.2	14.7	7.98	0.086

^aRate constants for each step in the pathway are given as derived in fitting experiments A, B and C shown in Figure 5. Global fitting was done sequentially as described in the text: Exp A alone, then Exp A plus Exp B, then Exps A, B and C fit simultaneously. This illustrates the progression of knowledge as additional experiments are performed. The final solution gives k_cat = 6.3 s⁻¹, k_cat/K_m = 2.6 μM⁻¹s⁻¹ and K_m = 2.4 μM, consistent with the steady state measurements. The row marked “Simulated” indicates the rate constants used to generate the synthetic data.

^bIn fitting experiments A and B simultaneously, two local minima in χ² were found in different areas of parameter space giving the two sets of rate constants listed. The first with irreversible substrate binding requires a rapid equilibrium chemistry step with K₂ = 0.52, while the second requires rapid equilibrium substrate binding with 1/K₁ = 11 μM.

^cFor these rate constants, there is only a lower limit set by the data. The data can be fitted as long as the rate constants are greater than the value listed and are maintained in a constant ratio with the reverse rate constant, e.g, k₋₁/k₁ = 11 μM in row 3.

This exercise also illustrates another important use of computer simulation. Experiments can be simulated and synthetic data generated in planning experiments or comparing models to published data. In addition it provides an ideal method for teaching kinetics using “dry labs” and problem solving through data fitting. The free student version of KinTek Explorer allows synthetic data to be generated and given to students in the form of a blank mechanism file that can opened with the student version of KinTek Explorer or exported as a text file for fitting using other programs. The file used to generate and fit the data given in Figure 5 are available in the “3-experiments.mec” file that is among the examples provided with the software.

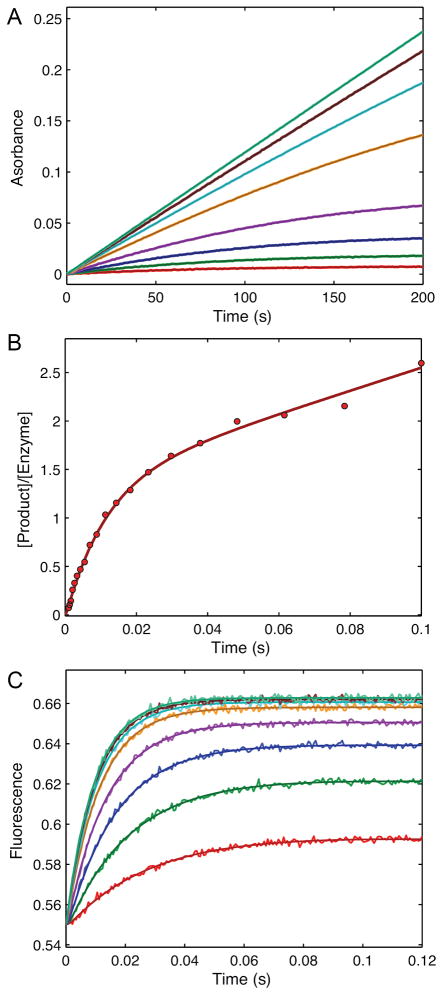
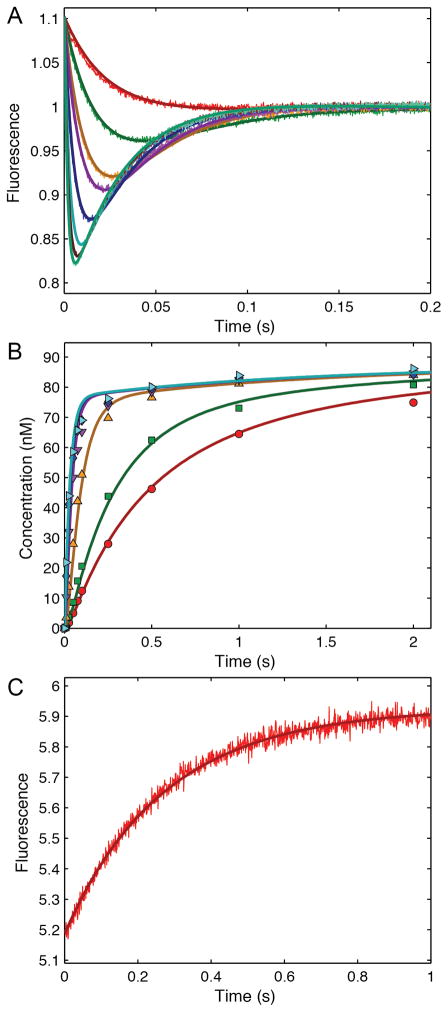
Figure 5. Information content of kinetic data.

This figure shows synthetic data designed to illustrate the information content of various kinetic experiments. A. Steady state kinetics with 0.5 μM enzyme reacting with 0.2, 0.5, 1, 2, 5, 10, 20, and 50 μM substrate. The signal was observed as absorbance due to product with an extinction coefficient of 0.04 μM⁻¹, such that the observable signal is equal to 0.04*[P]. B. Presteady state burst experiment simulated with 2 μM enzyme mixed with 50 μM substrate. The observable signal is the sum of [EP] + [P]. C. A stopped-flow fluorescence signal was simulated with 1 μM enzyme mixed with 2, 5, 10, 20, 50, 100, 200, and 500 μM substrate. The signal, as simulated and derived independently during data fitting was defined by f1*([E] + f2*[ES] + f3*[EP]), indicated that the protein fluorescence change was due to conformational changes occurring with the formation of product. The fluorescence scaling factors derived to be: f1 = 0.55 and f2 = 1 and f3 = 1.26, indicating a 26% increase in fluorescence with chemistry, but no change upon substrate binding. The smooth curves through the data were calculated by simulation from the global fit to the data according to Scheme 2 and the rate constants listed in Table 3. Individual fits to experiments A and B were indistinguishable visually from the global fits shown here and are not shown. Data and simulation are available in the “3_experiments.mec” file in the examples folder of the free student version of KinTek Explorer that can be downloaded at www.kintek-corp.com.

Experiment A (Figure 5A) is a simple steady state kinetic experiment observed by monitoring an absorbance change due to formation of product. The data over the first 20 seconds of reaction were fit to a straight line and the rate was plotted versus substrate concentration to obtain k_cat and k_cat/K_m values of 6.3 s⁻¹ and 2.6 μM⁻¹s⁻¹, respectively (Table 3). If care is not taken to restrict the data fitting to the initial linear portion, the k_cat/K_m values are underestimated due to curvature at longer times. In this exercise, after fitting by the traditional initial velocity approach, the full reaction time course at each concentration was then fit globally by simulation. The fitted curves superimpose on the data and are difficult to distinguish at the magnification shown in this figure. Fitting according to Case 1 described above gives estimates of k₁ ≥ k_cat/K_m = 2.6 μM⁻¹s⁻¹ and k₂, k₃ ≥ k_cat = 6.3 s⁻¹. We chose to fit to derive estimates for k_cat and k_cat/K_m (as in Case 1) rather than k_cat and K_m because k_cat/K_m provides a lower limit on the magnitude of k₁ (Table 3).

Experiment B (Figure 5B) shows the results of a presteady-state burst of product formation measured using rapid chemical quench-flow methods. The time dependence of product formation can be fit to a burst equation to derive estimates of the rates of chemistry and product release.

$$\frac{{[P]}_{\mathit{obs}}}{{[E]}_0}=\frac{[EP]-[P]}{{[E]}_0}=A_0(1-e^{-\lambda t})+k_{\mathit{cat}}t$$ Eqn 4

This equation assumes that there is a single step limiting the rate of formation of product at the active site, which could be achieved at sufficiently high substrate concentration. In practice, the burst experiment is initially performed at a substrate concentration much greater than the K_m, based upon steady state measurements, but additional data may be needed to establish that binding is faster than chemistry, as described below. Fitting by nonlinear regression, provides estimates of the rate and amplitude of the exponential burst phase and k_cat from the linear phase. Each variable in the burst equation is a function of all three rate constants:

$$\begin{array}{l}\lambda =k_2+k_{-2}+k_3=92.7s^{-1}\\ A_0=\frac{k_2(k_2+k_{-2})}{{(k_2+k_{-2}+k_3)}^2}=\frac{1.42\mu M}{2\mu M}=0.71\\ k_{\mathit{cat}}=\frac{k_2{k}_3}{k_2+k_{-2}+k_3}=\frac{11.6\mu M/s}{2\mu M}=5.8s^{-1}\end{array}$$

Simultaneous solution of these three equations affords estimates for each of the three rate constants: k₂= 71.5 s⁻¹, k₋₂= 13.7 s⁻¹ and k₄= 7.5 s⁻¹. The presteady state burst experiment provides a wealth of new information. It shows that product release is rate-limiting and provides estimates for the rate of the forward and reverse rates of the chemistry step, and its equilibrium constant. If product release had been faster than chemistry, there would have been no burst of product formation, and accordingly, the data would have supported the conclusion that k_cat provided a measure of the rate of chemistry or a step before chemistry. Thus the presteady-state burst experiment provides valuable additional information beyond what can be determined by steady state methods and directly addresses questions pertaining to events occurring at the active site of the enzyme.

Data fitting based upon simulation circumvents the convoluted analysis to resolve the three rate constants from the amplitude and rate of the burst. Moreover, by simultaneously fitting the data in experiments A and B, one can derive estimates for each of the rate constants that are consistent with both the steady state and presteady-state data. However, there is still some ambiguity in the parameters governing substrate binding versus chemistry in that two local minima in χ² could be found in different areas of parameter space. In one set of parameters, if substrate binding was assumed to be defined by k_cat/K_m, then the rate of chemistry must be fast; otherwise one would see a lag in the formation of product due to the slow rate of substrate binding (Table 3, row 2). Alternatively, one could fit the data with rapid equilibrium substrate binding followed by slower chemistry (Table 3, row 3). The number of data points and signal:noise ratio of rapid quench data generally do not allow resolution of a lag phase, so one must rely upon other methods to monitor the rate of substrate binding. Note that in fitting the data to the burst equation (Eqn 4), we assumed that substrate binding was faster than chemistry. Fitting by simulation revealed that the burst data could be explained by rate-limiting substrate binding or chemistry. One could distinguish the two models by performing a series of burst experiments at various substrate concentrations, or by pulse chase experiments (25, 26). Alternatively, one might be able to monitor substrate binding kinetics by stopped-flow fluorescence methods, if there is a change in protein fluorescence occurring naturally, or by the addition of a label to the enzyme, or a label in the substrate (24, 27–30). Here we show the hypothetical results of a protein fluorescence change.

Figure 5C shows the simulated results of a stopped-flow fluorescence experiment perform over a series of substrate concentrations. The fluorescence time dependence can be fit to a single exponential:

$$Y=A_1·e^{-{\lambda }_1·t}+c$$ Eqn 5

The absence of a detectable lag in the traces suggests that substrate binding is a rapid equilibrium reaction preceding chemistry. The concentration dependence of the rate fits a hyperbola providing estimates for the K_d (1/K₁) for substrate binding and the maximum rate of the fluorescence change, which is defined by the sum of k₂ + k₋₂ + k₃ (Scheme 2). In addition, the intercept provides an estimate of the net dissociation rate (k_off = k₋₂ + k₃) and the initial slope defines the apparent second order rate constant for substrate binding (k_on = K₁k₂).

$$\begin{array}{l}{\lambda }_1=\frac{K_1{k}_2[S]}{K_1[S]+1}+k_{-2}+k_3\\ k_2=78s^{-1}\\ k_{-2}+k_3=27.9s^{-1}\\ 1/K_1=13.7\mu M\end{array}$$

These data can be fit globally by simulation by defining the output signal to be a function of changes in fluorescence occurring upon or after substrate binding by the general formula: signal = f1*(E + f2*ES + f3*EP). Moreover, these data can be fit globally along with experiments A and B to achieve a final set of parameters that are consistent will all three experiments. This global fitting defines a correlation between the rate of chemistry and the maximum rate of the protein fluorescence change indicating that the fluorescence change is attributable to change occurring coincident with the chemistry step, and not during substrate binding (f2 = 1, f3 = 1.26). Thus, one does not assume which step leads to a change in fluorescence; rather, proper fitting reveals the step. Moreover, the concentration dependence of the rate of the fluorescence change resolves the alternative models in favor of the rapid equilibrium substrate binding followed by chemistry.

The final global fitting of the three experiments simultaneously provides reliable estimates for all six rate constants in the pathway and reproduces the constants that were used to simulate the data. Moreover, the fitted parameters yield steady state kinetic parameters consistent with those obtained by the original fitting of the steady state data.

$$\begin{array}{c}{k}_{\mathit{cat}}=\frac{k_2{k}_3}{k_2+k_{-2}+k_3}=6.29s^{-1}\\ K_m=\frac{k_2{k}_3+k_{-1}(k_{-2}+k_3)}{k_1(k_2+k_{-2}+k_3)}=2.37\mu M\\ k_{\mathit{cat}}/K_m=k_1\frac{k_2{k}_3}{k_2{k}_3+k_{-1}(k_{-2}+k_3)}2.65\mu M^{-1}{s}^{-1}\end{array}$$

The rate of product rebinding is defined largely by the approach to equilibrium at the lower concentrations of substrate in Figure 5A, and confidence contour analysis (not shown) indicate that its value is not as well determined as implied by the standard error analysis. Full time course kinetic analysis over a range of substrate concentrations, or after the addition of fixed concentrations of product would better define k₋₃.

This analysis shows that three straightforward experiments are sufficient to resolve the rates of substrate binding, chemistry and product release. Accordingly, this subset of experiments allows questions to be addressed regarding the binding of substrates at the active site of an enzyme and mechanisms of catalysis proposed by examination of the structure. This protocol overcomes the common, but ambiguous interpretation of changes in k_cat and K_m due to active site mutations, for example.

Single turnover kinetics

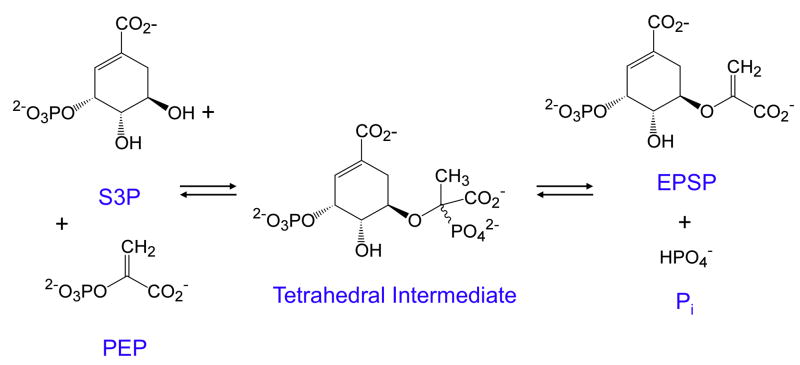
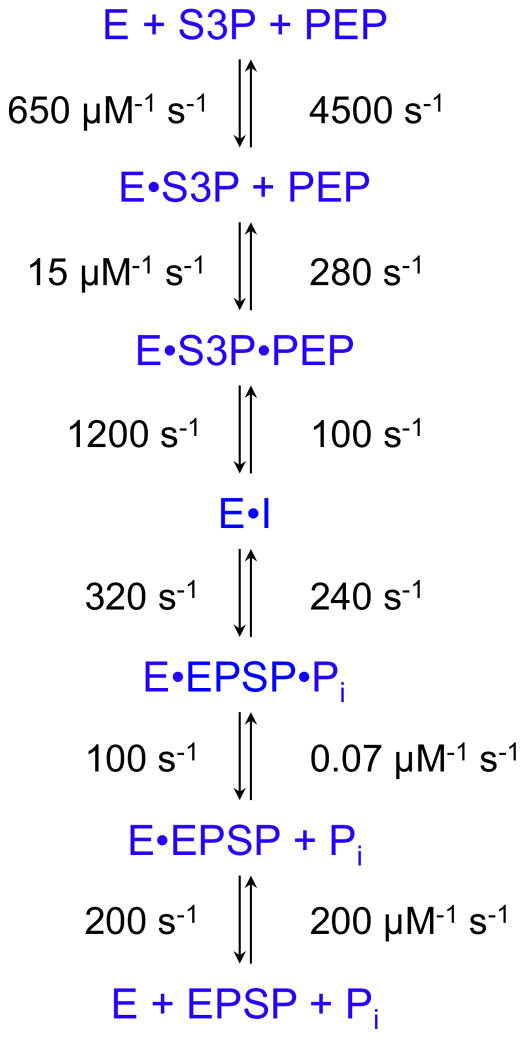
One of the first applications of computer simulation to derive a complete reaction sequence was in studies on EPSP (5-enoylpyruvoylshikimate-3-phosphate) synthase (EC 2.5.1.19) leading to the identification and isolation of a non-covalent tetrahedral intermediate and estimates for all 12 rate constants in the pathway (31–36). The reaction catalyzed by EPSP synthase is a simple addition/elimination reaction shown in Figure 6. The enzyme catalyzes both the formation and the breakdown of the intermediate with rate constants summarized in Scheme 3. Numerous experiments were conducted in order to establish the enzyme reaction pathway, including steady state kinetic studies to show ordered substrate binding and product release, isotope exchange kinetics, stopped-flow fluorescence studies on the binding of S3P (shikimate 3-phosphate) and the herbicide, glyphosate (reviewed in (32)). However, the most informative studies were conducted using rapid-chemical quench methods to study the presteady-state burst, and single turnover experiments of the reaction in the forward and reverse directions (Figure 7). In addition, the overall equilibrium constant and the internal equilibrium constants for the chemical transformations at the active site of the enzyme (K₃ and K₄) were determined by quantification of products resolved by ion exchange chromatography using radiolabeled substrates. All of this information was combined in globally fitting the entire data set based upon computer simulation (34).

Figure 6. Reaction catalyzed by EPSP synthase.

The reaction is shown in which S3P (shikimate 3-phosphate) reacts with PEP (phosphoenolpyruvate) to form EPSP (5-enoylpyruvoylshikimate-3-phosphate) and phosphate.

Scheme 3.

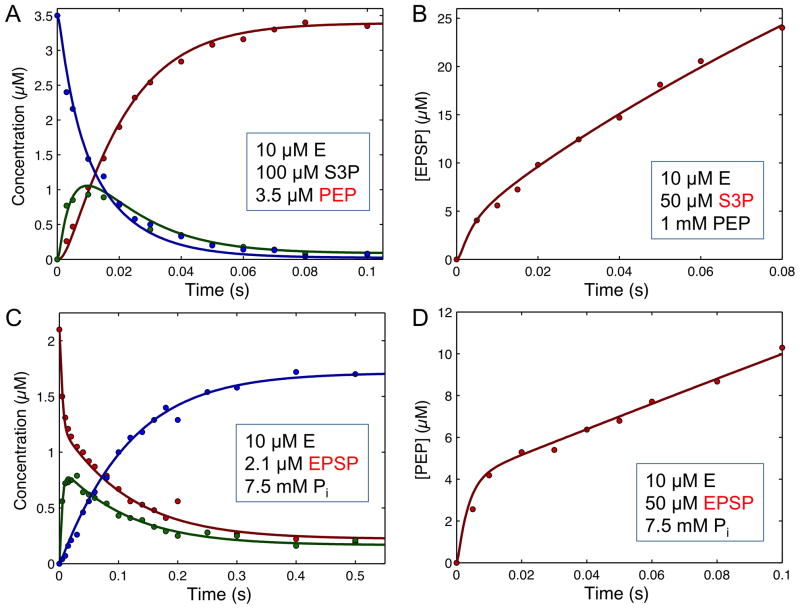
Figure 7. EPSP presteady-state and single turnover kinetics.

A. Single turnover in the forward direction. B. Presteady state burst in the forward direction. C. Single turnover of the reaction in the reverse direction. D. Presteady state burst in the reverse direction. The inset to each figure gives the starting concentration of reach reactant, and the species shown in red contains the radiolabel. Redrawn with permission from (34). The smooth lines were calculated by simulation according to the pathway and rate constants given in Scheme 3. Data and simulations are available in the “EPSP.mec” KinTek Explorer example file.

Figures 7B and D show the kinetics of a presteady state burst of product formation for the reaction in the forward and reverse directions, respectively. In each case, the data demonstrate that a reaction after chemistry is at least partially rate limiting, but the amplitude of the burst was small, approximately 40% of the enzyme concentration. The most informative are single turnover experiments shown in Figures 7A and C, in which the radiolabeled substrate was mixed with an excess of enzyme. These single turnover rapid-quench kinetic experiments revealed the formation and decay of the intermediate, leading to its isolation and identification. Moreover, the data establish the kinetic competence of the intermediate by showing that it is formed and decays at a rate sufficient to account for the depletion of the substrate and formation of the product. Single turnover kinetic experiments provide such rich information content because kinetically significant steps are revealed as 100% of the substrate binds to the enzyme and reacts to form intermediates and then product all in a single enzyme cycle. It is important to note that conventional fitting of these data would have been un-interpretable because the observed rates of formation and decay of the intermediate are complex functions of multiple rate constants and the amplitude provides essential information to resolve the rates. Analysis of these reaction kinetics by computer simulation resulted in a solution that accounts for both the rate and amplitude of each reaction, as well as equilibrium and the steady state kinetic measurements.

Enzyme Structure and Dynamics

The ultimate goal of modern kinetic analysis is to understand the role of enzyme structure in activity. This review ends with a brief summary of our recent work to address the role of substrate-induced conformational changes in enzyme specificity. We address this question using DNA polymerases as a model system because the alternative substrates are well known and specificity is of paramount importance. In addition, DNA polymerases allow single turnover kinetic studies to be performed with ease. In mixing an enzyme-DNA complex with a single nucleoside triphosphate (dNTP), only one reaction occurs because the next templating base will code for a mismatch, which binds weakly and reacts slowly.

The role of induced-fit in enzyme specificity has been controversial, including suggestions that a two-step binding sequence cannot contribute to specificity more than onestep binding (37), but that conclusion was based upon the assumption that initial binding and the conformational change step were in rapid equilibrium and faster than chemistry. We sought to address this question by attaching an environmentally sensitive fluorophore to the nucleotide recognition domain of HIV reverse transcriptase (HIVRT, EC 2.7.7.49) as shown in Figure 8 (24, 38). Positioned on the surface of the protein, the fluorescent label does not perturb the kinetics of the reaction, but provides a signal to monitor changes in protein structure from open to closed states after binding nucleotide.

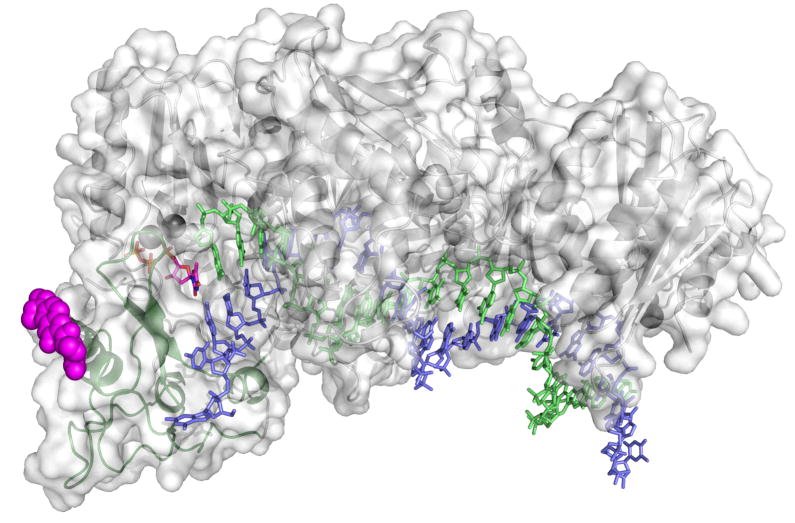
Figure 8. Structure of fluorescently labeled HIVRT.

The structure of HIVRT was rendered in pymol from 1rtd.pdb (39). The position of the fluorescent label (magenta spheres) was docked at the position of the E36C substitution (24). Duplex DNA is in blue (template) and green (primer), while the incoming nucleotide is magenta (sticks).

The results of one experiment are shown in Figure 9A. After mixing TTP with an HIVRT-DNA complex, there is a decrease in fluorescence followed by an increase, representing a single turnover in which the enzyme binds substrate, closes, catalyzes chemistry and then opens. Figure 9B shows the results of a rapid-quench flow experiment to monitor the time dependence of the chemical reaction. Fitting both curves simultaneously demonstrates that the slow rise of the fluorescence transient is coincident with the rate of the chemical reaction, implying fast opening after chemistry. In studies not shown, the binding of TTP to an enzyme- DNA_dd complex (where the DNA was terminated by a dideoxynucleotide to prevent chemistry) the fluorescence decreased rapidly in forming the closed E-DNA_dd-TTP complex, corresponding to that seen by crystallography (24, 39). Finally, an experiment was done to measure the release of bound TTP from a pre-formed E-DNA_dd-TTP complex (Figure 9C). After mixing with an excess of unlabeled E-DNA complex, there is an increase in fluorescence providing a measurement of the rate of enzyme opening to release TTP. These three experiments were fit globally to derive the pathway shown in Scheme 4, where ED and FD represent the open and closed states of the enzyme-DNA complex, respectively.

Figure 9. HIVRT kinetics.

A. Fluorescently labeled HIVRT in complex with duplex DNA (200nM MDCC-labeled HIVRT with 300 nM DNA) was mixed with various concentrations of TTP (2, 4, 10, 20, 40, 60, 80, and 100 μM) in a stopped-flow and the time course of fluorescence was recorded. B. Rapid quench-flow methods were used to measure the time dependence of the chemical reaction after mixing the HIVRT-DNA complex (150nMMDCC-labeled HIVRT with 100nM DNA) with various concentrations of TTP (0.25, 0.5, 2, 10, 25, and 100 μM). Redrawn with permission from (38). Smooth curves show the global fit to all of the date according to Scheme 4.

Scheme 4.

Surprisingly, because the rate of TTP release is slow relative to chemistry, the specificity constant for the enzyme is equal to the second order rate constant for substrate binding, determined by the initial weak substrate binding and the rate of the conformational change.

$$\begin{array}{l}{k}_{\mathit{cat}}/K_m=K_1{k}_2=7.5\mu M^{-1}{s}^{-1}\\ k_{\mathit{cat}}=k_3=34s^{-1}\\ K_m=\frac{k_{\mathit{cat}}}{k_{\mathit{cat}}/K_m}\approx \frac{k_3}{K_1{k}_2}=4.7\mu M\\ K_{d,\mathit{net}}=1/K_1(1+K_2)=0.4\mu M\end{array}$$

The rate of chemistry cancels from the expression for k_cat/K_m because k₃ is in both the numerator and denominator. Moreover, K_m is determined by the ratio of k_cat and the substrate binding rate (K₁k₂). Contrary to previous theories, these results indicate that the substrate-induced conformational change is a major determinant of enzyme specificity. The specificity constant for correct nucleotide incorporation is governed by the nucleotide affinity in the initial weak binding to the open state and the rate of the conformational change to form the closed state. This unexpected result implies that specificity is determined by the most ephemeral of states that are most difficult to study directly, the initial weak binding and the rate of the conformational change. Therefore, in order to understand the molecular details underlying the substrate-induced conformational change, we have followed up these studies by extensive molecular dynamics simulations (40). These simulations accurately predict the rates of the conformational change in the forward and reverse directions and reveal new details at atomic resolution.

Much of the debate regarding the role of induced fit in enzyme specificity over the past few decades was due to the lack of definitive data. Steady state kinetic analysis could not resolve the issue and so theoretical arguments abounded. Single turnover kinetic studies provided the direct measurement of events that dictate the fate of substrate after the initial binding step and thereby define the molecular events that determine specificity.

Summary

Here I have provided a brief history of enzyme kinetics from its beginnings a century ago to modern applications of kinetic analysis of enzyme reaction pathways that are made possible by the use of transient-state kinetic methods and computer-based data fitting routines. I have only hit some of the highlights of advances in kinetic data analysis over the last few decades using examples from my own lab. Certainly many others have contributed important, insightful and instructive examples that could have easily illustrated major advances in methods of analysis and information to define enzyme catalysis. For example, I have not discussed the use of singular value decomposition (SVD) to deconvolute time-resolved spectra, which is certainly an important technical advance (41). In recent collaborative work, we have simultaneously fit, stopped-flow fluorescence transients, rapid-quench-flow data, and SVD analysis of time resolve absorbance measurements to deduce a unique branched enzyme pathway (42).

It is interesting to note that the constant derived by Michaelis and Menten in the analysis of the full time course kinetics was not the Michaelis constant, but rather, V_max/K_m. In some sense it was a historical accident to define the steady state equation in terms of k_cat and K_m values, resulting in confusion over the interpretation of K_m. Because of the importance of k_cat/K_m in determining enzyme specificity, efficiency and proficiency (43), it would have been better if the equation had been defined in terms of the two primary constants, k_cat and “ k_cat/K_m”, such that K_m was simply the ratio of the two.

Scientists and historians often dream of time travel. In this brief review of the history of enzyme kinetic data analysis, it is amusing to think of what Leonor Michaelis and Maud Menten would think of our current methods of data analysis. No doubt they would be astounded at how the click of a computer mouse can trigger millions of calculations to be completed in seconds to find an optimal global fit involving a rather complex kinetic model and multiple data sets, or that molecular dynamics simulations of the motions of atoms could predict the molecular details of reactions governing enzyme specificity. Nonetheless, they would be justifiably proud of their accomplishments and pleased at how their work has stood the test of such advanced computational analysis. It is now our turn to ponder the new discoveries of the next century and wonder whether our work will stand the test of new scientific advances.

Abbreviations Used

EPSP

5-enoylpyruvoylshikimate-3-phosphate

HIVRT

HIV reverse transciptase

MDCC

7-diethylamino-3-[([(2-maleimidyl)ethyl]amino)carbonyl]coumarin

S3P

shikimate 3-phosphate