Abstract
Tissue-engineered (TE) cartilage constructs tend to develop inhomogeneously, thus, to predict the mechanical performance of the tissue, conventional biomechanical testing, which yields average material properties, is of limited value. Rather, techniques for evaluating regional and depth-dependent properties of TE cartilage, preferably non-destructively, are required. The purpose of this study was to build upon our previous results and to investigate the feasibility of using ultrasound elastography to non-destructively assess the depth-dependent biomechanical characteristics of TE cartilage while in a sterile bioreactor. As a proof-of-concept, and to standardize an assessment protocol, a well-characterized three-layered hydrogel construct was used as a surrogate for TE cartilage, and was studied under controlled incremental compressions. The strain field of the construct predicted by elastography was then validated by comparison with a poroelastic finite-element analysis (FEA). On average, the differences between the strains predicted by elastography and the FEA were within 10%. Subsequently engineered cartilage tissue was evaluated in the same test fixture. Results from these examinations showed internal regions where the local strain was 1–2 orders of magnitude greater than that near the surface. These studies document the feasibility of using ultrasound to evaluate the mechanical behaviors of maturing TE constructs in a sterile environment.
Keywords: Mechanical properties, Depth-dependent deformation, Acoustic methods, Multimodal evaluation, Bioreactor
INTRODUCTION
Osteoarthritis, a degenerative disease of cartilage, is a leading cause of disability in the industrialized world19,28,36 and tissue-engineered (TE) cartilage is a potential treatment for osteoarthritis. TE constructs are expected to possess mechanical properties that are similar to those of native cartilage if they are to maintain long-term functionality. Thus, there is a need for development of measurement technologies to assess TE products prior to implantation.
Current methods for evaluating native cartilage are of limited value for evaluating TE cartilage prior to implantation, and there are no formal criteria to certify whether a specific TE construct is ready for implantation.21 TE constructs tend to develop inhomogeneously. As a result, conventional biomechanical testing (e.g., confined, unconfined compression and indentation), which yield average material properties of the specimen, are of limited value for such constructs. Rather, techniques for evaluating regional and depth-dependent properties of TE cartilage, preferably non-destructively, are required.
Ultrasound is thought to be nondestructive, and has been used by others for quantitative evaluation of the regeneration process of TE cartilage, (e.g., by Hattori et al.7), but it has not been used for biomechanical assessments of intrinsic properties. In previous work in our laboratories, we proposed using ultrasound as a nondestructive method for determining material properties of hydrogels with the intent of extending this to TE cartilage.20,37As TE cartilage is acoustically inhomogeneous,38 it may be feasible to use ultrasound elastography to track deformations of internal inhomogeneities. In principle, this could allow for identification of internal material properties of developing tissue.
The purpose of this study was to investigate the feasibility of using ultrasound elastography to evaluate properties of tissues in a bioreactor. For validation purposes, we used stacked hydrogels with known properties, but with different concentrations to simulate inhomogeneities. Using time-shifts between pre- and post-compression signals, and, recognizing that time-shifts correspond to displacements, strains were calculated. Results were compared to those predicted from a finite-element analysis (FEA) of the construct.
MATERIALS AND METHODS
Test Samples
To mimic the stratified structure often seen in TE cartilage, a three-layered hydrogel construct was used. Three mm thick by 12.7 mm diameter agarose hydrogel disks were prepared at 4 and 8% concentrations as described previously.37 These were stacked, with a 4% gel sandwiched between two 8% gels. This provided a well-defined change in acoustic impedance at the transitions between gels,37 which is the source of the reflection used in this study. The hydrogel constructs were US-tested on the same day that they were prepared.20,37 After the US-tests, the samples were stored in diH2O (the same vehicle as was used to cast the gels) at 4 °C for later mechanical testing. The samples were allowed to return to room temperature prior to testing.
For TE constructs, mesenchymal stem cells were obtained from healthy volunteer donors under the terms of an IRB-approved protocol. The cells were culture-expanded until the end of second passage in Dulbecco's modified Eagle's medium with 1 g/L glucose (DMEM-LG, Invitrogen, Carlsbad, CA) with 10% fetal bovine serum from a lot selected as described previously (FBS, Sigma Chemical Corp., St. Louis, MO) and supplemented with 10 ng/mL FGF-2.11,32 (Note that FGF-2 is used only in the expansion medium).32 The cells were then vacuum-seeded at 6 × 107 cells/mL onto 12 mm diameter by 2 mm thick collagen-chondroitin sulfate porous scaffolds.13 The constructs were grown in sealed bioreactors with gas permeable 0.127 mm thick silicone membranes (McMaster-Carr, Cleveland, OH). The bioreactors (Fig. 1) were perfused continuously at 250 μL/h with fresh chondrogenic medium (DMEM-HG supplemented with 1% ITS+ Premix (6.25 μg/mL insulin, 6.25 μg/mL transferrin, 6.25 ng/mL selenious acid, 1.25 mg/mL serum albumin, and 5.35 μg/mL linoleic acid, BD biosciences, Franklin Lakes, NJ), 37.5 μg/mL ascorbate-2-phosphate (WAKO, Richmond, VA), 10−7 M dexamethasone, and 10 ng/mL TGFβ-1 (Peprotech, Rocky Hill, NJ), as well as 1% each l-glutamine, antibiotic antimycotic (10,000 units/mL penicillin G sodium, 10 mg/mL streptomycin sulfate, and 25 μg/mL amphotericin B in 0.85% saline), non-essential amino acids, and sodium pyruvate. Each week, over a three-week period, bioreactors were removed from the incubator and placed in the same test rig that was used to evaluate hydrogels in our previous study.20 The bioreactor and TE cartilage were sandwiched between the acoustic reflector and US transducer, similar to configuration used for hydrogels (see below, Test Procedure). However, for tissues, the apparatus contacted the bioreactor's gas permeable membranes. The membranes were acoustically coupled to the apparatus using coupling gel (Aquasonic 100, Parker Labs, Fairfield, NJ). Throughout this process, the tissue was maintained in culture medium in the sterile environment of the bioreactor.
FIGURE 1.
12 mm diameter cell-seeded construct grown in a perfusion bioreactor for 3 weeks.
Test Procedure
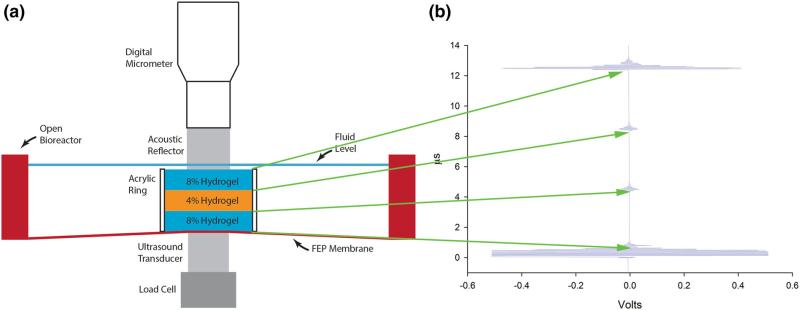
Hydrogel and TE constructs were evaluated using the device previously described (Fig. 2a).20 Briefly, the apparatus consists of a rigid frame (Minitec, Victor, NY) which aligns a sample stage between a load cell (Omegadyne LCMFD-10N, associated controller DP25B-S-A, Omega Engineering, Stamford, CT) and ultrasound transducer (Olympus V208-RM 20 MHz, Olympus NDT, Waltham, MA), at the bottom, and a polished acoustic reflector at the top. As in previous investigations a Panametrics 5072PR pulser-receiver (Olympus NDT) was used (pulse repeat frequency 1 kHz, signal energy 13 μJ, damping 100 Ω, and gain 0 dB).20 An Agilent DSO-X 2012A 100 MHz oscilloscope (Agilent Technologies, Santa Clara, CA) was used for data acquisition at 0.1 G samples/s. The load cell/transducer assembly and the reflector were maintained in coaxial alignment. The height of the load cell/transducer assembly is axially adjustable, so that the top of the transducer touched the bottom membrane of the bioreactor; it was then fixed in place during the experiment. The reflector was positioned axially using a micrometer-driven linear stage (M4004-DM, Parker-Hannifin, Cleveland, OH). The layered construct was placed in deionized water in an open bioreactor in the test rig (Fig. 2a).20 The reflector contacted the top of hydrogel samples or the top membrane of the bioreactor for TE sample. Acoustic coupling gel was used at all contacts with bioreactor membranes.
FIGURE 2.
(a) Schematic illustration of the custom designed elastography test rig: a three-layered construct was formed from three agarose hydrogels which were cast individually, stacked up, and then held by an acrylic ring (16 mm outer diameter, 12.7 mm inner diameter, 10 mm height) to prevent sliding. The top and bottom layers were 8% gels and the middle was a 4% gel. The gel stack was placed in a bioreactor chamber (without the top membrane, for convenience) and sandwiched between a micrometer-positioned acoustic reflector and the ultrasound transducer. A load cell was in-line with the transducer. (b) The ultrasound A-mode echogram of the three-layered construct before compression. The first, (lowermost) waveform is the reflection from the interface between the bioreactor membrane and the bottom 8% gel. The second waveform is the reflection from the lower interface between the bottom 8% gel and the middle 4% gel. The third waveform is the reflection from the upper interface between the middle 4% gel and the top 8% gel. The upper-most waveform is the reflection from the interface between the top 8% gel and the acoustic reflector.
Zeroes were established for time of US reflections and sample thickness as described previously.20 Using this approach, the thickness of a sample is always known. For all samples, ultrasound reflections (Fig. 2b) were captured at least one minute after the compression was applied.
For hydrogels, four compressive displacements steps (40 μm displacement per step) were applied using the micrometer. The first step was a tare displacement that created close contact among the gel layers. This ultrasound-compression procedure was repeated 11 times.
For TE cartilage, the procedure was the same except that three 50-μm compression steps were applied. The samples remained in the sealed bioreactor for the entire process.
Depth-Dependent Axial Strain from Ultrasound Elastography
Local internal displacement and strain were estimated for each compression step using time-domain elastography.20,30,41 Cross-correlation was used to obtain time delays between ultrasound signals at 0 μm compression (X = {x(0), x(1), ..., x(N – 1)}), and at 40, 80, 120 and 160 μm compression (Y = {y(0), y(1),..., y(N – 1)}) for gel samples, and 50, 100 and 150 μm compression for the tissue engineered samples. The correlation coefficient between a tracking window (ROI) of the pre-compression signal and an A-mode echogram of the entire post-compression signal was computed using the normxcorr2 cross-correlation function in MATLAB (MathWorks, Natick, MA) as12,42:
| (1) |
where X̄ is the mean of X, and Ȳ is the mean of Y. The length of the ROI was 2 μs, beginning at 4, 8, and 12 μs for hydrogel constructs (based on the characteristic location of the echoes Fig. 2b), and 0.5 μs, beginning at 5.5, 6.5, 7, and 7.5 μs for TE cartilage. ROIs were chosen to include characteristic reflections. The ROI was then marched across the entire post-compression signal in 0.01 μs increments (the sampling period), and the correlation coefficient was computed at each increment. The point on the post-compression signal where the correlation coefficient was maximized determined the local time delay (Td) between the preand post-compression signals. To improve the estimation accuracy of Td, we upsampled the correlation coefficient function by a factor of 100, using low-pass interpolation (interp).1,3 This MATLAB code can be found in the Electronic Supplementary Materials, Part A.
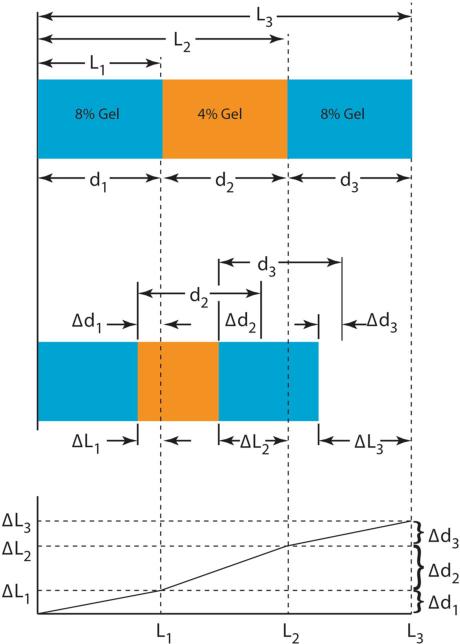
To relate strain to time delays, the system was modeled as a one-dimensional series of connected material layers corresponding to each layer of the three layer hydrogel construct, analogous to the spring model of Céspedes et al. (Figure 3).1 Note that in this investigation, the range of i is limited to 1–3, however, this approach can be extended to materials with more finely distributed inhomogeneities. The undeformed thicknesses of the hydrogel layers are described either using Li as the global coordinates or using di as the local coordinates. Lengths and changes in lengths have analogs to time-delay estimation in elastography: the ultrasonic analog of an undeformed length and a deformation is a reference time and a time delay, respectively. Lengths were computed as the product of the SOS and half the travel time through a region or time shift due to deformation. If is the travel time of the pre-compression signal at the top of the ith layer and is the time delay between pre- and post-compression signals at the top of the ith layer, then the global strain (εglobal) of the system and the local strain of the ith layer (εi) are (Fig. 3):
| (2) |
| (3) |
| (4) |
| (5) |
FIGURE 3.
Measurement of strain in three springs connected in series. Top and middle: configurations of 3-layer hydrogel constructs pre- and post-compression. Li are the uncompressed free length to the interfaces in a global coordinate system; di are the local thickness of each gel. ΔLi are the changes in Li, Δdi are the changes in di, both after compression. Bottom: local strains are the slopes of each segment the trace in the graph of deflection (ΔL) vs. free length (L).
Under the commonly used assumption that the SOS is constant, i.e., not a function of deformation, .
Equations (2)–(5) show that strains can be found from the slope of line, modified by the ratio of SOS in deformed and undeformed samples.
The sensitivity of the strain measurement to the time delays was investigated using the estimated time delay plus or minus the sampling period. This provided the range of allowable error in strain measurement using the original sampling period obtained from current hardware.
Poroelastic FEA of the Three-Layered Construct
To validate the strains predicted by elastography a poroelastic, finite-deformation finite-element contact model of the three-layered hydrogel construct was developed using COMSOL (Burlington, MA). Strains predicted by this model were compared with those predicted by ultrasound elastography. The acoustic reflector (radius Rr = 3.17 mm) was modeled as an elastic material (Young's modulus E = 200 GPa and Poisson's ratio v = 0.33). Poroelastic properties of the three gels (Table 1) were obtained using indentation.18,23 The porosity of each gel was estimated using the fluid volume fraction as in our previous studies.37 These properties were then used as inputs to the FEA.
TABLE 1.
Material properties of three hydrogel layers measured by indentation.
| Young's modulus (Pa) | Poisson's ratio | Permeability (m4 N–1 s–1) | |
|---|---|---|---|
| Top 8% gel | 684634.55 | 0.22178 | 1.755 × 10–14 |
| Middle 4% gel | 220407.42 | 0.22178 | 2.519 × 10–14 |
| Bottom 8% gel | 683673.59 | 0.22178 | 1.312 × 10–14 |
These values were the input for the FEA of the three-layered hydrogel construct (Fig. 6).
The contact between the reflector (source boundary) and the top gel (destination boundary) was modeled as a “contact pair” without friction but with equal normal displacements using a penalty method. At the base of the bottom gel, a roller constraint (free slip in the horizontal direction while zero displacement in the vertical direction) was prescribed for the portion of the surface that was supported by the ultrasound transducer, radius Rt = 2.94 mm. To enforce displacement and flow continuity on all shared interfaces, “identity pairs” connecting all components were created. A contact pair defined for the penalty method was imposed between the elastic and poroelastic subdomains, i.e., the reflector and the three-layered construct. Free-flow boundary conditions, (“Atmosphere/Gage”) were prescribed on all exterior surfaces of the three-layered construct except for the interface between it and the reflector, and the interface between it and the transducer, where no flow boundaries were imposed.
In the model, the compressive displacement was applied to the top of the reflector, as in the procedure for ultrasound testing: four equal 40-μm compression steps, each applied over 1 s, followed by a relaxation period of 59 s. For comparison with strains determined using elastography, local strains predicted by FEA were averaged through the thickness of each gel under the transducer.
This ultrasound-compression testing configuration was similar to an indentation test except that the base of the three-layered construct was free in the radial direction. The FEA was verified by comparison with an indentation stress-relaxation model that was developed by Spilker et al., which is described in Electronic Supplemental Materials, Part B.33
RESULTS
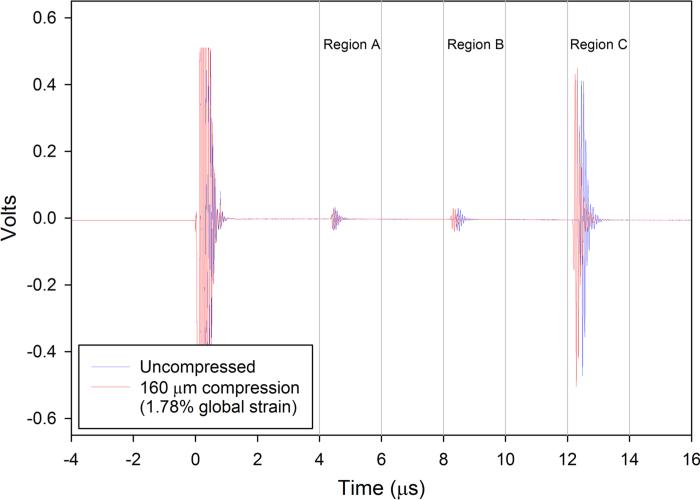
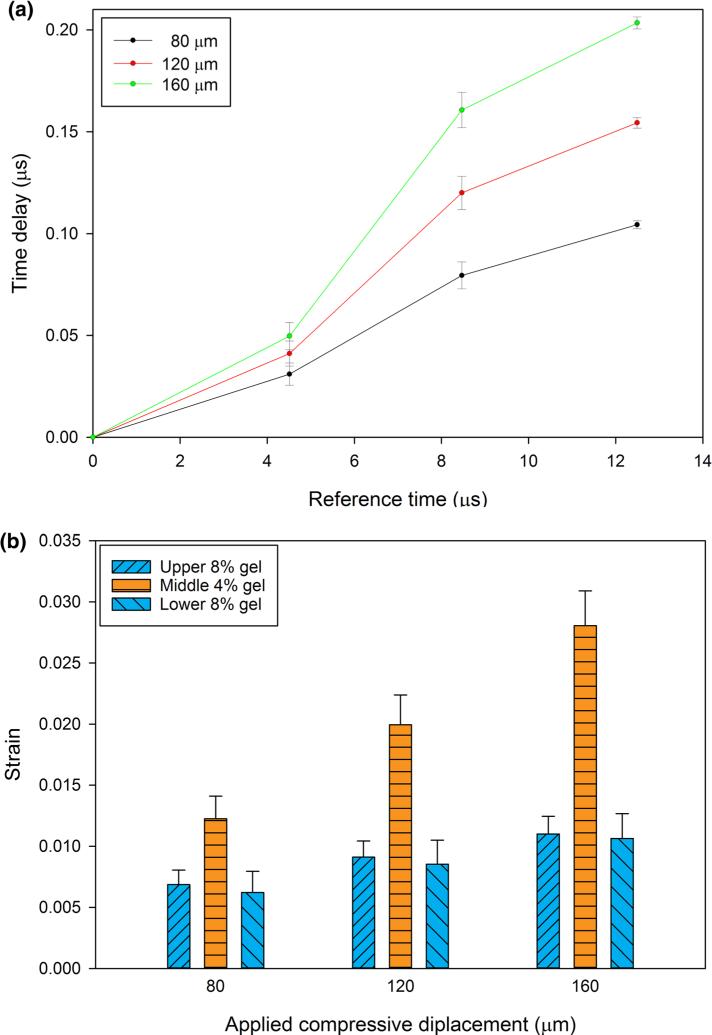
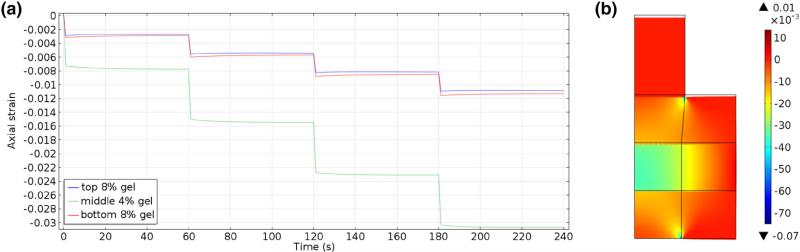
Well-defined reflections from the interfaces between gels, and the interface between the top 8% gel and acoustic reflector were found (Fig. 2b). These echoes shifted in time as the construct was compressed (Fig. 4). Each interface established a region of interest where cross-correlation was used to determine time delays. The time delays corresponding to the regions of interest as functions of the reference times showed similar strain (slopes) for the two 8% gels bounding the construct, and a larger strain (steeper slope) for the 4% gel in the center of the construct (Fig. 5a). These slopes, which correspond to the local longitudinal strain in each gel (Eqs. (3)–(5)), show that deformation in the more compliant 4% gel was greater than that in the stiffer 8% gels (Fig. 5b).
FIGURE 4.
Ultrasound echoes from the internal and external boundaries of the three-layered hydrogel construct under 0 (blue) and 160 μm compression (red). The other three steps (40, 80, and 120 μm) are not shown in this figure. The maximum value of the normalized cross-correlation function was used to calculate the time delay between pre- and post-compression signals within a ROI. Three ROI windows (a 4–6 μs, b 8–10 μs, and c 12–14 μs) were selected to track the time shifts of the echoes reflected from the interfaces of the bottom to the middle gel, the middle to the top gel and the top gel to the acoustic reflector, respectively.
FIGURE 5.
(a) Strains computed as in Eqs. (3)–(5) for four 40-μm compression steps. (The first 40-μm step was used to ensure contact, and is not shown). (b) Average local strains of a three-hydrogel stack, predicted by ultrasound elastography, after four incremental compressions (again, the first increment is not shown). The error bars in (a and b) represent the standard deviations of 11 repeated trials.
Excellent agreement was found between the three-layer FEA, as a model of indentation, and the model in Spilker et al. (see Electronic Supplementary Materials, Part B).33 Qualitatively, strains predicted by FEA mirrored those predicted by elastography. As expected, the strain in the 4% gel layer was greater than that in the 8% gel layers whose strains were almost equal to each other (Fig. 6).
FIGURE 6.
Simulated strain fields (COMSOL) in a three-layered construct as used in ultrasound elastography testing for a sequence of four 40 μm ramp compressions (0.44% global strain per step): (a) History of the averaged strain across each layer for the prescribed ramp compressions. (b) Strain map at the end of the fourth step (160 μm, 1.78% global strain, 240 s test time).
Quantitative differences in the local internal strains predicted by ultrasound elastography and the FEA were, on average, smallest for the bottom 8% gel (Table 2). The average differences between the top 8% and middle 4% gels are more then two times greater than those for the bottom gel (Table 2, rows two through four below the table header). In general, the differences between predicted strains were reduced as the incremental compression was increased. At the highest displacement, 160 μm, the relative percent difference for local strain of each layer was less than ten percent. These results were computed under the assumption that the SOS is constant. However, previous measurements have shown that the SOS in gels is not constant, but decreases with increasing compression. To account for compression dependent SOS, Equations for strain Eqs. (2)–(5) should be modified by the ratio of cd and cr: the sounds speed under pre- and post-compression, respectively. From the linear correlation between sound speed and applied deflection for different concentrations,20 the ratio (cd/cr) at 3.2% strain for 4% and 8% gels were 0.9982 and 0.9951, respectively. The effect of the correction for compression, for gels, is small (Table 2, last row).
TABLE 2.
Local strains predicted by the FEA and from ultrasound elastography (US) for the last three steps of applied compression on the top of the three-layered gel construct.
| Strain top 8% gel |
Strain middle 4% gel |
Strain bottom 8% gel |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Comp. (μm) | FEA | US | % | FEA | US | % | FEA | US | % |
| 80 | 0.00551 | 0.00686 ± 0.00118 | 19.6 | 0.01483 | 0.01225 ± 0.00185 | –21.0 | 0.00596 | 0.00620 ± 0.00174 | 3.87 |
| 120 | 0.00815 | 0.00911 ± 0.00133 | 10.5 | 0.02237 | 0.01995 ± 0.00243 | –12.1 | 0.00868 | 0.00853 ± 0.00197 | –1.75 |
| 160 | 0.01086 | 0.01100 ± 0.00145 | 1.27 | 0.03003 | 0.02806 ± 0.00284 | –7.02 | 0.01149 | 0.01063 ± 0.00203 | –8.09 |
| 160 | 0.01086 | 0.0109 | 0.367 | 0.03003 | 0.02792 | –7.56 | 0.01149 | 0.0105 | –9.42 |
Each 40 μm compression increment translates to a global strain of 0.44%. The first step is not shown. Local strains in rows two though four were computed under the assumption the SOS was constant in the gels, which is a common assumption in elastography. In the last row, the predicted strain is corrected for the decrease in SOS with compression. For these hydrogels, the effect of compression-dependent SOS on the strains is small. Percent differences in strain between two methods, FEA and US, were, on average, lowest for the largest, 160 μm, compression step. The percent difference was calculated using , where was the mean of the strains computed from ultrasound elastography.
In contrast to local strain, differences in the global strain of the three-layered construct between the model and the elastography were under ten percent for all displacement increments (Table 3).
TABLE 3.
Predicted global strains (ε) and ultrasound elastography strains (US) for the last three steps of applied compression of the three-layered gel construct.
| Global strain of the three-layered hydrogel construct |
|||
|---|---|---|---|
| Compression (μm) | ε | US | % |
| 80 | 8.889 × 10–3 | (8.358 ± 0.1582) × 10–3 | –6.35 |
| 120 | 1.333 × 10–2 | (1.236 ± 0.0209) × 10–2 | –7.85 |
| 160 | 1.778 × 10–2 | (1.629 ± 0.0237) × 10–2 | –9.15 |
Each 40 μm compression increment translates to a global strain of 0.44%. The first step is not shown. The percent difference was calculated using , where was the mean of US. Global strain (ε) is the change in thickness divided by the original thickness of the whole three-layered construct. Percent differences in strain between the two methods, ε and US, were all less than 10%.
Varying the predicted time delay by plus or minus one sampling period resulted in a wide range of predicted strain for each layer and at each level of applied compression (Table 4). For each level of compression, and for each layer, the range predicted by varying the time delay bracketed the strains predicted by FEA and ultrasound elastography.
TABLE 4.
Local strains predicted from ultrasound elastography using Eqs. (3)–(5), where the estimated time delay was ± the sampling period, i.e., , i = 1, 2, 3 at each step.
| Comp. (μm) | Strain top 8% gel | Strain middle 4% gel | Strain bottom 8% gel |
|---|---|---|---|
| 80 | 0.00464–0.00908 | 0.00719–0.01729 | 0.00123–0.01117 |
| 120 | 0.00689–0.01132 | 0.01489–0.02500 | 0.00356–0.01351 |
| 160 | 0.00878–0.01322 | 0.02301–0.03311 | 0.00566–0.01561 |
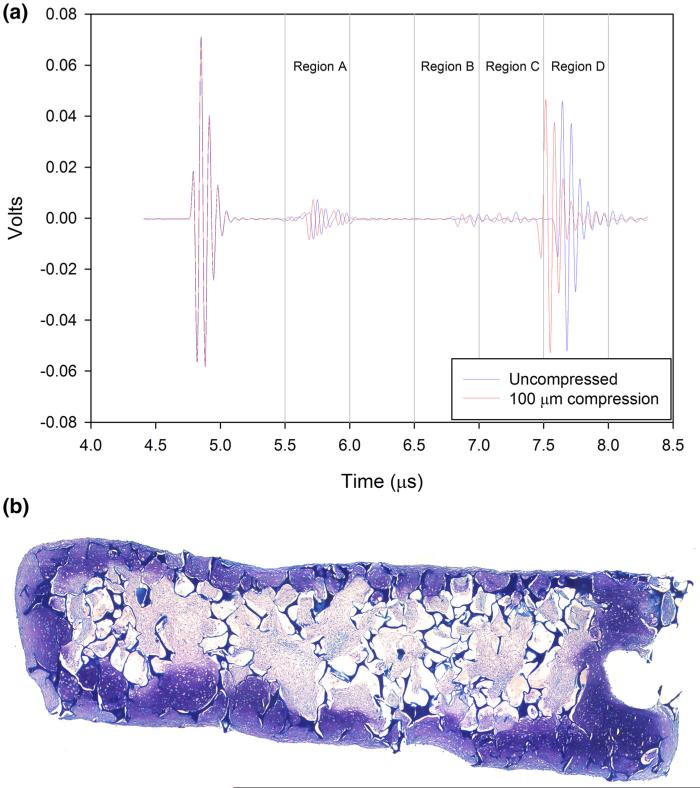
In tissue engineered cartilage multiple echoes were also found, which is consistent with the stratified structure often seen in these tissues.38 These echoes shifted as compression was applied (Fig. 7; Table 5). The shift was greatest at the reflector and negligible at the transducer side of the sample. Strain was greatest in Region B, and was approximately twice that in region A. Strain in regions C and D, close to the tissue's surface were the lowest.
FIGURE 7.
A-mode ultrasound signals from TE cartilage, showing a time shift to the left of internal acoustic reflections due to inhomogeneities in the tissue at 100 μm compression (shorter times, red trace), from zero compression (blue trace). Note expected negligible displacement at the transducer (left). Regions A to D are ROIs encompassing the reflections and used in regional strain computations (Table 5).
TABLE 5.
Internal strain in TE cartilage for each region in Fig. 7 for each compression step.
| Region | 50 μm compression | 100 μm compression | 150 μm compression |
|---|---|---|---|
| A | 2.264 × 10–2 | 4.661 × 10–2 | 6.947 × 10–2 |
| B | 5.004 × 10–2 | 9.721 × 10–2 | 1.508 × 10–1 |
| C | 3.624 × 10–3 | 6.919 × 10–3 | 9.604 × 10–3 |
| D | 3.422 × 10–3 | 3.734 × 10–3 | 8.416 × 10–3 |
DISCUSSION
The investigation was motivated by the realization that the mechanical properties of TE cartilage should be evaluated prior to implantation. Most assessments of the quality of TE products, for example histology or biomechanics, are either destructive or violate the sterile bioreactor environment and, as a result, cannot be implanted. Additionally, evaluations such as unconfined compression or indentation can take 4 h per specimen and are, thus, impractical. As noted, the goal of our series of studies has been to develop nondestructive evaluation of mechanical properties of developing TE cartilage.17,20,21,37 By using elastography it should be possible to identify highly compliant regions within developing TE constructs, which correlate with histologically immature tissue. Constructs with such features should be eliminated as candidates for implantation.
We chose to investigate the use of ultrasound elastography for nondestructive evaluation of tissues in a bioreactor, although we note that MRI can provide morphological assessments and has been used to determine deformation fields in native and engineered cartilage5,24–27 There are advantages and disadvantages to each system. Ultrasound measurements are completed in seconds rather than minutes, and do not require dedicated, non-magnetic bioreactor components. The apparatus does not require a shielded room, which allows it to be conveniently located adjacent to the culture facility, and overall the hardware and infrastructure used for ultrasound is orders of magnitude less costly than for MRI. Overall, ultrasound is simple to use, which makes it attractive for production level measurements of tissue quality. A potential advantage of MRI is the ability to track internal displacement in materials that are acoustically homogeneous where ultrasound elastography cannot be used.
Ultrasound clearly delivers some energy to the irradiated tissue, but diagnostic ultrasound, such as this, is commonly used in clinical imaging, and is generally regarded as innocuous. On the other hand, in laboratory experiments, ultrasound has elicited some anabolic, hence beneficial cellular responses in MSCs and chondrocytes. For example, low intensity ultra-sound has been shown to stimulate cartilage matrix formation by rabbit MSCs, including type II collagen synthesis, aggrecan synthesis and to inhibit the production of catabolic enzymes, e.g., matrix metalloproteinase-2 expression.10 Similar results have been reported for chick and human chondrocytes4,34,40 and MSCs.6,31 In general, in these studies, the intensity of the ultrasound was of similar or greater magnitude to that used here, while the duration of the ultrasound application was much longer than in our studies, e.g., 20–40 min/per day or longer vs. 1–2 min/day.2,31,34,40 At a transducer center-frequency of nominally 20 MHz, we are also outside of the 5 MHz peak resonant frequency described for mammalian cells, thus minimizing ultrasound-mediated cellular stress.6,16 Therefore, we do not anticipate any major effects on tissue development through our intermittent US probing; if any, we would predict that they would be in line with the existing literature, i.e., beneficial, and certainly do not expect a destructive effect.
In previous work, we detected obvious ultrasound reflections in TE cartilage due to internal inhomogeneity.38 This was in contrast to healthy native cartilage that was acoustically homogeneous.38 This suggested that these ultrasound reflections could be used to calculate depth-dependent strain using nondestructive elastography. We should note that at higher frequencies, internal reflections have been observed in native cartilage, but at the possible expense of depth of penetration.41,44
Using ultrasound elastography, we showed that within a tissue engineered construct some regions are more compliant than others (Fig. 7). Using inverse modeling, it would be possible to determine local material properties. At this point, it is not clear which tissue properties are more valuable in terms of predicting performance of a TE cartilage sample, e.g., local strain or local material properties. One advantage of material properties is that approximate target values are known from native tissue, which then provides a good comparison with engineered cartilage. However, we have data that strongly suggest that local strain concentrations due to inhomogeneities in the ECM distribution in the tissue is a very significant contributor to failure under combined sliding and compression.22,39 To test the feasibility of identifying inadequate constructs, we used ultrasound elastography and numerical simulation to estimate local strains in three-layered hydrogel constructs or TE cartilage. As a proof-of-concept, agarose hydrogels were used as surrogates for TE cartilage since they are not only fluid-saturated poroelastic materials but also highly reproducible, less expensive and can be prepared more quickly than TE cartilage.20,37 A layered hydrogel construct with outer layers of 8% gel and an inner 4% gel layer were tested. The inner layer was more compliant than the outer layers, which simulates developing TE cartilage.
In this investigation, elastography was implemented using time-domain cross-correlation of signals reflected from gels or tissues before and after compression. This approach has been used to evaluate internal strain in a number of soft tissues including native articular cartilage.29,43 Although time-domain cross-correlation is widely used, alternative spectral implementations of elastography have been developed. Spectral methods may be less affected by noise, and may be able to image larger strains than time domain cross correlation.8,9,35 The applicability of such methods for evaluating tissues in a bioreactor is the topic of future investigations.
LIMITATIONS
An FEA model of the three-layered hydrogel construct was developed to provide an estimate for validating the strains predicted from elastography. Any FEA model is based on a number of assumptions, and discrepancies between the local strains obtained from ultrasound elastography with those calculated from the FEA might be explained by these assumptions or by limitations of the measurements.
For example, since it is impractical to bond hydrogel layers together, a retaining ring was used to align the three gel layers. While layered constructs could be made by sequentially casting layers of different concentrations of agarose in the same mold, for this study we wanted to retain control of the spatial dimensions in order to validate our measurement approach.5 Layered casting makes this difficult; furthermore the new layer tends to melt into the existing layer causing a more gradual transition and thus a loss of the sharp discontinuity. The resulting (unknown a priori) gradient of properties would be difficult to model, which was again important for the proof of concept study. For simplicity, the stacked layers were modeled as continuous in the FEA (i.e., as if they were bonded together) and flow and displacement were assumed to be continuous at the interfaces. In principle, the unattached interfaces between layers in the hydrogel construct would result in quicker stress relaxation (lower strains) than in the model. Conversely, including a retaining ring around the three-layered construct would stiffen the entire construct, which would cause the actual strains in the sample to be less than those predicted by the model. In practice, the observed differences between the strains in the FEA model and the elastography did not show a consistent bias.
An additional source of error in elastography was the temporal resolution of the reflected signals. Temporal resolution is limited by the sampling rate of the oscilloscope which is 0.1 G samples/s. This means that we can, at best, capture the timing of signal peaks to within plus or minus half a sampling period. This gives rise to a range of strain (Table 4). However, in all cases the elastography strains were within the limits predicted by ±1 sampling period. Although the differences in Table 2 may appear large, this suggests that the limitation is not in the algorithm but rather in the hardware, and increasing the sampling rate of the oscilloscope should improve the estimate of the time delay and, thus, of the strain. Ultrasound and MRI methods appear to be similar in terms of the precision of the computed strain. For example, Neu and Walton define absolute strain precision as the standard deviation of the strain over repeated measurements.27 In cartilage, they found strain precision of 0.17% using DENSE with FSE pulse sequences. In the layered agarose system used here, the standard deviation in the strains averaged over all displacements and all layers was 0.19% (Table 2). Although similar, a direct comparison of strain precision cannot be made since these are measured on two different materials.
The FEA was also developed under the assumption of axisymmetric conditions. However, in ultrasound testing, the compression was not necessarily applied exactly at the center of hydrogel construct. Applying compression off center would result in greater strain in the construct than predicted by the model. In any case, actual TE samples are unlikely to be axisymmetric.
An inherent limitation of elastography, as described by Ophir et al.,30 is the assumption of constant SOS in the tested sample. Measurements performed in our lab and others have shown that the SOS in hydrogels decreases with the applied compression.20 Therefore, the ratio of cd to cr Eqs. (2)–(5) is not equal to one. We previously described a linear correlation between SOS and applied deflection for different concentrations20; from this study, the ratios (cd/cr) of SOS measured at 3.2% strain to SOS measured at 0% strain for 4 and 8% gels were 0.9982 and 0.9951, respectively. Although probably negligible in hydrogels, the effect of strain on SOS is greater in native cartilage,14,15 and this effect likely cannot be neglected in TE cartilage. This is especially the case as the mechanical properties of engineered products approach those of native cartilage. The accuracy of ultrasound elastography measurements might be improved if the effects of compression on SOS could be taken into account.
This paper describes a proof of concept experiment and focuses on validating this approach along one axis. Clearly, in the future the single-element transducer could be replaced with a 1- or 2-D array to expand the capabilities of the system. This would require additional data acquisition equipment and more sophisticated signal processing. We are exploring these options at this time. Additional expansions could include using transducers in more than one plane to derive, e.g., Poisson's ratio of the samples.
CONCLUSIONS
Ultrasound elastography was implemented and validated to measure the axial strain within layered gel constructs. The approach was then applied to TE constructs in a sealed bioreactor as proof of the feasibility of using ultrasound elastography to nondestructively evaluate the mechanical behaviors of maturing TE constructs in a sterile environment. This approach provides depth-dependent evaluation in tissues with internal inhomogeneities and complements our previous studies that are well-suited to acoustically homogeneous tissues.20,37
Supplementary Material
ACKNOWLEDGMENTS
Research reported in this publication was supported by the National Institute of Biomedical imaging and Bioengineering under award number R01 EB20367-01, and the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health under Awards Number P01 AR053622 (JMM, JFW, HB) and AR050208 (JFW). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Mr. Joseph Heebner was the recipient of an ENGAGE fellowship. Funding for ENGAGE 2013 came from the National Center for Regenerative Medicine (http://www.ncrm.us) and proceeds from MSC2011 conference (http://www.msc conference.net). We thank Alexander Lee Rivera for help with scaffold fabrication. The authors have no financial relationships that may cause a conflict of interest. We thank Dr. Victor M. Goldberg, to whom this paper is dedicated, for his interest and encouragement, and for providing the seed money for these studies.
Footnotes
ELECTRONIC SUPPLEMENTARY MATERIAL
The online version of this article (doi:10.1007/s10439-015-1356-x) contains supplementary material, which is available to authorized users.
REFERENCES
- 1.Céspedes I, Huang Y, Ophir J, Spratt S. Methods for estimation of subsample time delays of digitized echo signals. Ultrason. Imaging. 1995;17:142–171. doi: 10.1177/016173469501700204. [DOI] [PubMed] [Google Scholar]
- 2.Cook SD, Salkeld SL, Popich-Patron LS, Ryaby JP, Jones DG, Barrack RL. Improved cartilage repair after treatment with low-intensity pulsed ultrasound. Clin. Orthop. Relat. Res. 2001;391:S231–S243. doi: 10.1097/00003086-200110001-00022. [DOI] [PubMed] [Google Scholar]
- 3.de Korte CL, Céspedes EI, van der Steen AF, Pasterkamp G, Bom N. Intravascular ultrasound elastography: assessment and imaging of elastic properties of diseased arteries and vulnerable plaque. Eur. J. Ultrasound. 1998;7:219–224. doi: 10.1016/s0929-8266(98)00043-3. [DOI] [PubMed] [Google Scholar]
- 4.Ebisawa K, Hata K, Okada K, Kimata K, Ueda M, Torii S, Watanabe H. Ultrasound enhances transforming growth factor beta-mediated chondrocyte differentiation of human mesenchymal stem cells. Tissue Eng. 2004;10:921–929. doi: 10.1089/1076327041348437. [DOI] [PubMed] [Google Scholar]
- 5.Griebel AJ, Khoshgoftar M, Novak T, van Donkelaar CC, Neu CP. Direct noninvasive measurement and numerical modeling of depth-dependent strains in layered agarose constructs. J. Biomech. 2014;47:2149–2156. doi: 10.1016/j.jbiomech.2013.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.GuhaThakurta S, Budhiraja G, Subramanian A. Growth factor and ultrasound-assisted bioreactor synergism for human mesenchymal stem cell chondrogenesis. J. Tissue Eng. 2015;6:2041731414566529. doi: 10.1177/2041731414566529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hattori K, Ikeuchi K, Morita Y, Takakura Y. Quantitative ultrasonic assessment for detecting microscopic cartilage damage in osteoarthritis. Arthritis Res. Ther. 2005;7:R38–R46. doi: 10.1186/ar1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Konofagou EE, Varghese T, Ophir J. Spectral estimators in elastography. Ultrasonics. 2000;38:412–416. doi: 10.1016/s0041-624x(99)00116-x. [DOI] [PubMed] [Google Scholar]
- 9.Konofagou EE, Varghese T, Ophir J, Alam SK. Power spectral strain estimators in elastography. Ultra-sound Med. Biol. 1999;25:1115–1129. doi: 10.1016/s0301-5629(99)00061-7. [DOI] [PubMed] [Google Scholar]
- 10.Lee HJ, Choi BH, Min BH, Son YS, Park SR. Low-intensity ultrasound stimulation enhances chondrogenic differentiation in alginate culture of mesenchymal stem cells. Artif. Organs. 2006;30:707–715. doi: 10.1111/j.1525-1594.2006.00288.x. [DOI] [PubMed] [Google Scholar]
- 11.Lennon DP, Haynesworth SE, Bruder SP, Jaiswal N, Caplan AI. Human and animal mesenchymal progenitor cells from bone marrow: identification of serum for optimal selection and proliferation. In Vitro Cell Dev. Biol. Anim. 1996;32:602–611. [Google Scholar]
- 12.Lewis J. Fast normalized cross-correlation.. Canadian Image Processing and Pattern Recognition Society; Quebec City. 1995. [Google Scholar]
- 13.Liang WH, Kienitz BL, Penick KJ, Welter JF, Zawodzinski TA, Baskaran H. Concentrated collagen-chondroitin sulfate scaffolds for tissue engineering applications. J. Biomed. Mater. Res. A. 2010;94:1050–1060. doi: 10.1002/jbm.a.32774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lötjönen P, Julkunen P, Tiitu V, Jurvelin JS, Töyräs J. Ultrasound speed varies in articular cartilage under indentation loading. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011;58:2772–2780. doi: 10.1109/TUFFC.2011.2143. [DOI] [PubMed] [Google Scholar]
- 15.Lötjönen P, Julkunen P, Töyräs J, Lammi MJ, Jurvelin JS, Nieminen HJ. Strain-dependent modulation of ultrasound speed in articular cartilage under dynamic compression. Ultrasound Med. Biol. 2009;35:1177–1184. doi: 10.1016/j.ultrasmedbio.2009.03.002. [DOI] [PubMed] [Google Scholar]
- 16.Louw TM, Budhiraja G, Viljoen HJ, Subramanian A. Mechanotransduction of ultrasound is frequency dependent below the cavitation threshold. Ultrasound Med. Biol. 2013;39:1303–1319. doi: 10.1016/j.ultrasmedbio.2013.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lu XL, Sun DD, Guo XE, Chen FH, Lai WM, Mow VC. Indentation determined mechanoelectro-chemical properties and fixed charge density of articular cartilage. Ann. Biomed. Eng. 2004;32:370–379. doi: 10.1023/b:abme.0000017534.06921.24. [DOI] [PubMed] [Google Scholar]
- 18.Mak AF, Lai WM, Mow VC. Biphasic indentation of articular cartilage—I. Theoretical analysis. J. Biomech. 1987;20:703–714. doi: 10.1016/0021-9290(87)90036-4. [DOI] [PubMed] [Google Scholar]
- 19.Mannoni A, Briganti MP, Di Bari M, Ferrucci L, Costanzo S, Serni U, Masotti G, Marchionni N. Epidemiological profile of symptomatic osteoarthritis in older adults: a population based study in Dicomano, Italy. Ann. Rheum. Dis. 2003;62:576–578. doi: 10.1136/ard.62.6.576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mansour JM, Gu DW, Chung CY, Heebner J, Althans J, Abdalian S, Schluchter MD, Liu Y, Welter JF. Towards the feasibility of using ultrasound to determine mechanical properties of tissues in a bioreactor. Ann. Biomed. Eng. 2014;42:2190–2202. doi: 10.1007/s10439-014-1079-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mansour JM, Welter JF. Multimodal evaluation of tissue-engineered cartilage. J Med. Biol. Eng. 2013;33:1–16. doi: 10.5405/jmbe.1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Motavalli M, Whitney GA, Dennis JE, Mansour JM. Investigating a continuous shear strain function for depth-dependent properties of native and tissue engineering cartilage using pixel-size data. J. Mech. Behav. Biomed. Mater. 2013;28C:62–70. doi: 10.1016/j.jmbbm.2013.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mow VC, Gibbs MC, Lai WM, Zhu WB, Athanasiou KA. Biphasic indentation of articular cartilage—II. A numerical algorithm and an experimental study. J. Biomech. 1989;22:853–861. doi: 10.1016/0021-9290(89)90069-9. [DOI] [PubMed] [Google Scholar]
- 24.Neu CP, Hull ML, Walton JH. Error optimization of a three-dimensional magnetic resonance imaging tagging-based cartilage deformation technique. Magn. Reson. Med. Sci. 2005;54:1290–1294. doi: 10.1002/mrm.20669. [DOI] [PubMed] [Google Scholar]
- 25.Neu CP, Hull ML, Walton JH. Heterogeneous three-dimensional strain fields during unconfined cyclic compression in bovine articular cartilage explants. J. Orthop. Res. 2005;23:1390–1398. doi: 10.1016/j.orthres.2005.03.022.1100230622. [DOI] [PubMed] [Google Scholar]
- 26.Neu CP, Hull ML, Walton JH, Buono-core MH. MRI-based technique for determining nonuniform deformations throughout the volume of articular cartilage explants. Magn. Reson. Med. Sci. 2005;53:321–328. doi: 10.1002/mrm.20343. [DOI] [PubMed] [Google Scholar]
- 27.Neu CP, Walton JH. Displacement encoding for the measurement of cartilage deformation. Magn. Reson. Med. Sci. 2008;59:149–155. doi: 10.1002/mrm.21464. [DOI] [PubMed] [Google Scholar]
- 28.Nuesch E, Dieppe P, Reichenbach S, Williams S, Iff S, Juni P. All cause and disease specific mortality in patients with knee or hip osteoarthritis: population based cohort study. BMJ. 2011;342:d1165. doi: 10.1136/bmj.d1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ophir J, Alam SK, Garra B, Kallel F, Konofagou E, Krouskop T, Varghese T. Elastography: ultrasonic estimation and imaging of the elastic properties of tissues. Proc. Inst. Mech. Eng. H. 1999;213:203–233. doi: 10.1243/0954411991534933. [DOI] [PubMed] [Google Scholar]
- 30.Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrason. Imaging. 1991;13:111–134. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- 31.Schumann D, Kujat R, Zellner J, Angele MK, Nerlich M, Mayr E, Angele P. Treatment of human mesenchymal stem cells with pulsed low intensity ultra-sound enhances the chondrogenic phenotype in vitro. Biorheology. 2006;43:431–443. [PubMed] [Google Scholar]
- 32.Solchaga LA, Penick K, Porter JD, Goldberg VM, Caplan AI, Welter JF. FGF-2 enhances the mitotic and chondrogenic potentials of human adult bone marrow-derived mesenchymal stem cells. J. Cell. Physiol. 2005;203:398–409. doi: 10.1002/jcp.20238. [DOI] [PubMed] [Google Scholar]
- 33.Spilker RL, Suh JK, Mow VC. A finite element analysis of the indentation stress-relaxation response of linear biphasic articular cartilage. J. Biomech. Eng. 1992;114:191–201. doi: 10.1115/1.2891371. [DOI] [PubMed] [Google Scholar]
- 34.Tien YC, Lin SD, Chen CH, Lu CC, Su SJ, Chih TT. Effects of pulsed low-intensity ultrasound on human child chondrocytes. Ultrasound Med. Biol. 2008;34:1174–1181. doi: 10.1016/j.ultrasmedbio.2007.12.019. [DOI] [PubMed] [Google Scholar]
- 35.Varghese T, Konofagou EE, Ophir J, Alam SK, Bilgen M. Direct strain estimation in elastography using spectral cross-correlation. Ultrasound Med. Biol. 2000;26:1525–1537. doi: 10.1016/s0301-5629(00)00316-1. [DOI] [PubMed] [Google Scholar]
- 36.Verbrugge LM. Women, men, and osteoarthritis. Arthritis Care Res. 1995;8:212–220. doi: 10.1002/art.1790080404. [DOI] [PubMed] [Google Scholar]
- 37.Walker JM, Myers AM, Schluchter MD, Goldberg VM, Caplan AI, Berilla JA, Mansour JM, Welter JF. Nondestructive evaluation of hydrogel mechanical properties using ultrasound. Ann. Biomed. Eng. 2011;39:2521–2530. doi: 10.1007/s10439-011-0351-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Welter J, Citak M, Baskaran H, Caplan A, Goldberg V, Mansour J. Does acoustic homogeneity correlate with tissue quality in engineered cartilage?. OARSI World Congress on Osteoarthritis; San Diego, CA. 2011. [Google Scholar]
- 39.Whitney GA, Jayaraman K, Dennis JE, Mansour JM. Scaffold-free cartilage subjected to frictional shear stress demonstrates damage by cracking and surface peeling. J. Tissue Eng. Regen. Med. 2014 doi: 10.1002/term.1925. doi:10.1002/term.192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang ZJ, Huckle J, Francomano CA, Spencer RG. The effects of pulsed low-intensity ultrasound on chondrocyte viability, proliferation, gene expression and matrix production. Ultrasound Med. Biol. 2003;29:1645–1651. doi: 10.1016/j.ultrasmedbio.2003.08.011. [DOI] [PubMed] [Google Scholar]
- 41.Zheng YP, Bridal SL, Shi J, Saied A, Lu MH, Jaffre B, Mak AF, Laugier P. High resolution ultra-sound elastomicroscopy imaging of soft tissues: system development and feasibility. Phys. Med. Biol. 2004;49:3925–3938. doi: 10.1088/0031-9155/49/17/007. [DOI] [PubMed] [Google Scholar]
- 42.Zheng YP, Ding CX, Bai J, Mak AF, Qin L. Measurement of the layered compressive properties of trypsin-treated articular cartilage: an ultrasound investigation. Med. Biol. Eng. Comput. 2001;39:534–541. doi: 10.1007/BF02345143. [DOI] [PubMed] [Google Scholar]
- 43.Zheng YP, Mak AFT, Lau KP, Qin L. An ultrasonic measurement for in vitro depth-dependent equilibrium strains of articular cartilage in compression. Phys. Med. Biol. 2002;47:3165–3180. doi: 10.1088/0031-9155/47/17/308. [DOI] [PubMed] [Google Scholar]
- 44.Zheng YP, Niu HJ, Arthur Mak FT, Huang YP. Ultrasonic measurement of depth-dependent transient behaviors of articular cartilage under compression. J. Biomech. 2005;38:1830–1837. doi: 10.1016/j.jbiomech.2004.08.020. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.