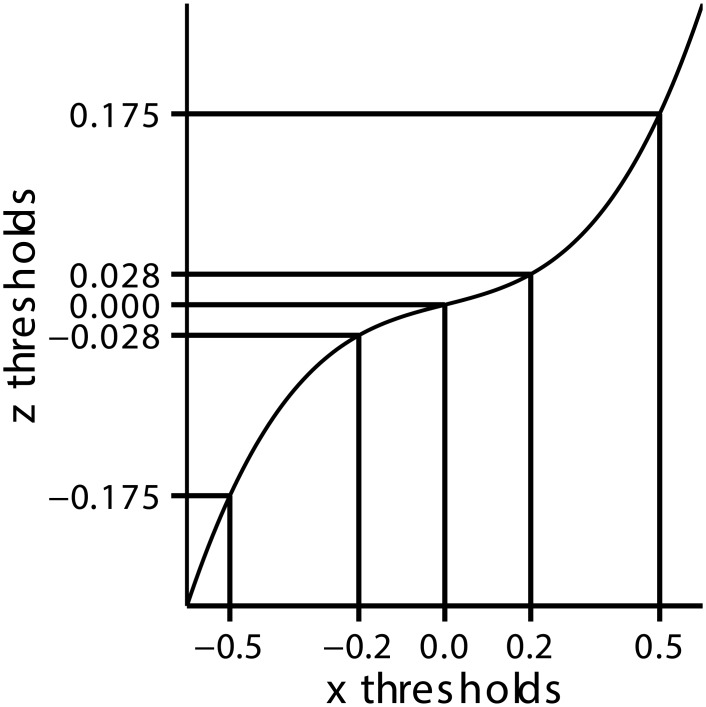
Fig 1. For one-dimensional sensory data, x, any monotonic transformation, z(x), can give the same mapping from x to c.

The best we, as experimenters, can do is to determine the mapping from x to c, which, for discrete mappings, corresponds to a set of thresholds (the vertical lines). We can, however, get the same mapping from x to c by first transforming x to z (the curved black line), then thresholding z. The relevant thresholds are simply given by passing the x-thresholds through z(x) (giving the horizontal lines). Therefore, there is no way to determine the “right” z(x)—any z(x) will fit the data (as long as z(x) is a strictly monotonic function of x).