Image-derived and arterial blood sampled input functions for quantitative PET imaging of the angiotensin II subtype 1 receptor in the kidney

Abstract

Purpose:

The radioligand ¹¹C-KR31173 has been introduced for positron emission tomography (PET) imaging of the angiotensin II subtype 1 receptor in the kidney in vivo. To study the biokinetics of ¹¹C-KR31173 with a compartmental model, the input function is needed. Collection and analysis of arterial blood samples are the established approach to obtain the input function but they are not feasible in patients with renal diseases. The goal of this study was to develop a quantitative technique that can provide an accurate image-derived input function (ID-IF) to replace the conventional invasive arterial sampling and test the method in pigs with the goal of translation into human studies.

Methods:

The experimental animals were injected with [¹¹C]KR31173 and scanned up to 90 min with dynamic PET. Arterial blood samples were collected for the artery derived input function (AD-IF) and used as a gold standard for ID-IF. Before PET, magnetic resonance angiography of the kidneys was obtained to provide the anatomical information required for derivation of the recovery coefficients in the abdominal aorta, a requirement for partial volume correction of the ID-IF. Different image reconstruction methods, filtered back projection (FBP) and ordered subset expectation maximization (OS-EM), were investigated for the best trade-off between bias and variance of the ID-IF. The effects of kidney uptakes on the quantitative accuracy of ID-IF were also studied. Biological variables such as red blood cell binding and radioligand metabolism were also taken into consideration. A single blood sample was used for calibration in the later phase of the input function.

Results:

In the first 2 min after injection, the OS-EM based ID-IF was found to be biased, and the bias was found to be induced by the kidney uptake. No such bias was found with the FBP based image reconstruction method. However, the OS-EM based image reconstruction was found to reduce variance in the subsequent phase of the ID-IF. The combined use of FBP and OS-EM resulted in reduced bias and noise. After performing all the necessary corrections, the areas under the curves (AUCs) of the AD-IF were close to that of the AD-IF (average AUC ratio =1 ± 0.08) during the early phase. When applied in a two-tissue-compartmental kinetic model, the average difference between the estimated model parameters from ID-IF and AD-IF was 10% which was within the error of the estimation method.

Conclusions:

The bias of radioligand concentration in the aorta from the OS-EM image reconstruction is significantly affected by radioligand uptake in the adjacent kidney and cannot be neglected for quantitative evaluation. With careful calibrations and corrections, the ID-IF derived from quantitative dynamic PET images can be used as the input function of the compartmental model to quantify the renal kinetics of ¹¹C-KR31173 in experimental animals and the authors intend to evaluate this method in future human studies.

1. INTRODUCTION

Positron emission tomography (PET) is an excellent imaging tool for quantitative investigation of central and peripheral receptors.¹ Dynamic PET imaging techniques and compartmental model analysis have been widely used for quantification of the biokinetics of radioligands in vivo.² In the present work, we carried out dynamic PET studies to quantify the binding of the radioligand ¹¹C-KR31173 to the renal angiotensin II subtype 1 receptor (AT₁R) in vivo,³ a potential biomarker for renovascular hypertension and progression of renal injury. Binding parameters in pigs were estimated from time activity curves using compartmental model analysis.

Compartmental model analysis requires both a tissue time activity curve (TAC) and an input function. Arterial blood samples are used to derive the input function, but this approach is invasive with potential side effects and difficult to carry out in patients with renal diseases. Alternative methods include a population based input function⁴ and an image-derived input function (ID-IF).⁵ ID-IF has the advantage of being noninvasive but suffers from inaccuracies caused by inferior image quality from dynamic PET scans.

Many studies of the ID-IF have been published for studies of the receptors in the brain^6–9 or heart¹⁰ but not in the kidneys. The partial volume effect (PVE) has been widely recognized as a factor affecting the accuracy of the ID-IF.¹¹ It has been shown that filtered back projection (FBP) and ordered subset expectation maximization (OS-EM) reconstruction techniques can also result in quantitative differences¹² but their effect is often neglected. In the present work, we investigated the effect of PVE correction methods and also the effect of image reconstruction algorithms. We also took into consideration the metabolism and red cell binding of the radiopharmaceutical.

2. METHODS

2.A. Image and data acquisition

Dynamic PET scans were carried out in six domestic pigs (average age 2.5 months). The animal protocol was approved by the Animal Care and Use Committee. Among six pigs, nine different scans were conducted. For each pig PET study, ∼0.74 GBq [¹¹C]KR31173 was injected and a 90 min dynamic 2D PET study of the kidneys was obtained using a GE Advance scanner. The scan time for each frame varied from 5 s to 5 min (Table I). The resolution of the scanner was determined using a physical phantom with point sources to be 6 mm, which was in agreement with the scanner specification. The artery derived input function (AD-IF) was used as reference and was measured from a total of forty 0.5 ml arterial blood samples. The activity of aliquot plasma samples was measured in a well counter cross-calibrated with the PET scanner. The sampling scheme was ∼5 s intervals in the early phase and up to 10 min in the late phase. All the measurements were decay corrected. A limited number of blood samples were also used to measure total blood activity and to calculate red cell binding. Venous blood samples were also collected at limited times and compared to the arterial blood samples. Magnetic resonance angiography (MRA) scans of the abdominal aorta and kidneys were acquired in the experimental animals for anatomical reference.

TABLE I.

Framing schedule for dynamic scan.

Scans	12	12	6	7	4	4	12	Total: 57
Scan time (s)	5	10	20	60	90	180	300	Total: 5400

2.B. Image processing and reconstruction

All PET data were corrected for crystal efficiency, dead time effects, random events, and radioactive decay. Attenuation correction was carried out with the help of a Ge-68 transmission scan. The pig images were reconstructed with both the FBP and OS-EM algorithms. The reconstructed image matrix size was 256*256 with pixel size of 2 mm and slice thickness of 4.25 mm. The OS-EM algorithm included 21 subsets and 2 iterations. A postsmoothing filter was not used in either methods. Scatter correction was applied to both image reconstruction methods.

2.C. Time activity curves and input function determination

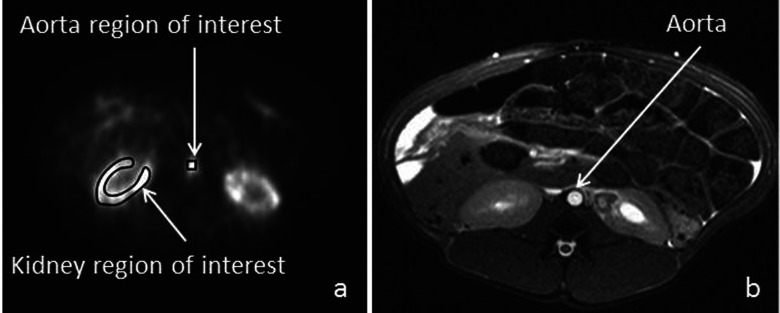
Kidney TACs were obtained from the renal cortex using manually drawn ROIs as shown in Fig. 1(a), which depicts a typical anatomical structure from a pig scan.

FIG. 1.

(a) An example of a ROI in the aorta as well as the kidney cortex from a dynamic PET scan in a pig. (b) MRA images from a pig study showing the normal anatomical structure of the aorta and kidneys.

The ID-IF was obtained from the average intensities of volumes-of-interest (VOI) of the abdominal aorta placed at the level of the kidneys in the dynamic 3D PET images [Fig. 1(a)]. The 3D VOI of the aorta was obtained by combining identical ROIs from five adjacent slices to reduce statistical noise. The 3*3 square ROI in the pig study included as much activity in the aorta as possible and excluded as much as background as possible. As the aorta may not be perpendicular to the imaging plane, the ROI was chosen slice by slice, and the resulting VOI was not a box. The size and shape of the VOI were also used as input parameters during partial volume correction described subsequently.

2.D. Effects of different reconstruction methods

The quantitative accuracy and precision of the ID-IFs obtained from the FBP and OS-EM reconstruction methods were investigated in pig studies and phantom studies.

ID-IFs from multiple pig studies were measured using both the FBP and OS-EM approaches. After applying the remaining corrections described in Sec. 2.E, the comparisons of FBP based ID-IF and OS-EM based ID-IF using AD-IF as gold standard were used to evaluate the bias and noise caused by different reconstruction approaches.

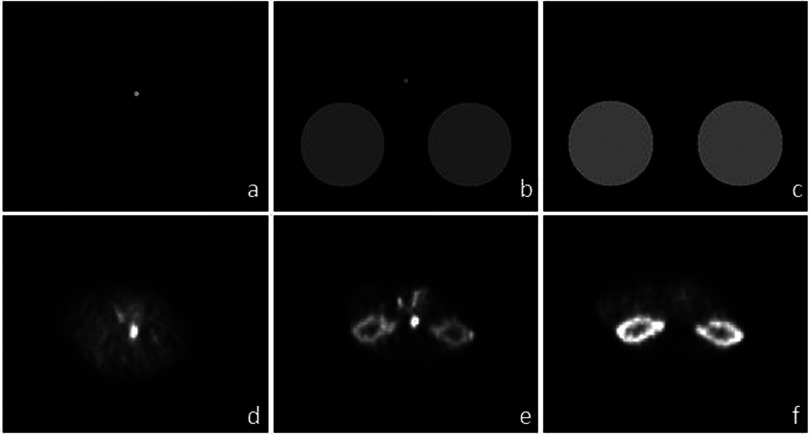
Simulation using dynamic digital phantoms with an equivalent level of noise was also included in our study to study the bias from iterative reconstruction approaches. Three time points of the phantom study are shown in Figs. 2(a)–2(c), corresponding to three time points of a typical pig scan shown in Figs. 2(d)–2(f). The two big circles represent the kidneys, while the small circle in the center represents the aorta. The activity density of the “kidney” and the “aorta” were set to values of the kidney and aorta measured in a pig study reconstructed with FBP at corresponding time points. To study the effects of kidney uptake on aortic activity, a second digital phantom with zero kidney uptake was also included. The activity level and noise level in the aorta for the second digital phantom were the same as in the first digital phantom. Using projection data from the phantom [Figs. 2(a)–2(c)], iterative image reconstruction methods including both maximum likelihood expectation maximization (ML-EM) and OS-EM using 21 subsets were performed. The number of updates was set at 210 (210 iterations for ML-EM and 10 iterations with 21 subsets for OS-EM) to avoid possible nonconvergent bias.¹³ Partial volume correction using the known phantom image was applied to the reconstructed activity in the aorta. The bias of ML-EM and OS-EM methods was calculated using the averaged results of 100 different noise realizations.

FIG. 2.

(a) A digital phantom ∼0.2 min postinjection, (b) digital phantom ∼1 min postinjection, (c) digital phantom after 2 min. (d) PET scan ∼0.2 min postinjection. (e) PET scan 1 min postinjection, (f) PET scan after 2 min. Images shown in (d)–(f) are reconstructed using OS-EM with 21 subsets and 2 updates. (b) and (e) show that the bias of OS-EM occurs in situations where the uptake in the kidney is similar to that of aorta.

Based on the results showed in Sec. 2.E, both FBP and OS-EM image reconstruction approaches were used for the ID-IF. During the first 2 min postinjection, the ID-IF was measured from images with the FBP method; the later phase was measured from images with the OS-EM method.

2.E. Partial volume correction

The quantitative accuracy of the activity in the aorta depends on the PVE due to its small size relative to the resolution of the PET system.¹⁴ That in turn will affect the quantitative accuracy of the entire ID-IF. The partial volume effect includes both activity spill-in and spill-out. In the early phase (the first 3 min including 24 time points in the dynamic scan) of our dynamic studies, the activity in the aorta was much higher than that in the surrounding background, and spill-out of activity to the surrounding background is the dominant effect. In the late phase (the rest of the scan including 33 time points in the dynamic scan), the activity in aorta was lower than background; hence, the spill-in from the surrounding background is the dominant effect. The recovery coefficient (RC) method was used for correcting PVE. The method can be represented by the following formula:¹⁵

$${\displaystyle {\mathrm{IF}}_{\text{measured}}\left(t\right)={\mathrm{RC}}^{\ast }{\mathrm{IF}}_{\mathrm{truth}}\left(t\right)+\text{background}{\left(t\right)}^{\ast }\text{spillover},}$$ (1)

where IF_measured(t) is the summed image intensity of the VOI over the aorta at time t, RC is the fraction of true activity that remains in the VOI, IF_truth(t) is the true activity of the VOI, and background(t)*spillover is the amount of background activity spilled into the VOI. The RC was estimated from a digital phantom study with an object distribution similar to the aorta in the PET studies. The anatomical shape of the aorta and the aortic VOI was determined using MRA images as shown in Fig. 1(b) and the resolution of the PET.

The recovery coefficients were estimated by simulation that was based on the measured diameter of the abdominal aorta, the shape of the ROI, and the resolution of the PET system. The aorta was represented by a cylinder and background activity was set to zero. Since the activity spill-out effect was negligible along the vertical axis and mainly existed in the horizontal plane, it was possible to simplify the VOI into a ROI. The shape of the ROI was the same as the one used for measurement of the aorta activity from the reconstructed images. A Gaussian smoothing filter with the FWHM of 6 mm was applied to simulate the spill out effects; the FWHM was chosen to match the resolution of the scanner. The recovery coefficient was obtained by dividing the average value in the ROI by the original activity level.

To take into consideration the spillover coefficient, the equation for ID-IF was modified as

$${\displaystyle {\mathrm{IF}}_{\mathrm{measured}}\left(t\right)={\text{RC}}^{\ast }{\mathrm{IF}}_{\mathrm{truth}}\left(t\right)+\text{background}\_\text{term},}$$ (2)

where the background_term was assumed to be a constant and was estimated using a single sample point. The calibration point was acquired by measuring the activity level in the vein 60 min after injection. When a venous sample was not available, a population based calibration point obtained by averaging the artery blood sample at 60 min was used. The background_term was calculated from the calibration point using Eq. (3). The correction of spillover effects on ID-IF was done by subtracting the calculated background_term from the measured data as shown in Eq. (2),

$${\displaystyle \text{background}\_\text{term}={\mathrm{IF}}_{\mathrm{measured}}\left(60\text{min}\right)-{\text{RC}}^{\ast }\text{calibration point}.}$$ (3)

2.F. Biological corrections of the input function

The measured activity derived from the aorta VOI represents activity from whole blood, while in a compartment model, the input function is plasma activity. Red cell binding and hematocrit (HCT) were measured to convert the VOI data from whole blood activity to plasma activity using the following formula:¹⁶

$${\displaystyle C_{\text{plasma}}\left(t\right)=\frac{C_{\text{blood}}{\left(t\right)}^{*}\left(1-\text{RBC}\_\text{binding}\left(t\right)\right)}{1-\text{HCT}},}$$ (4)

where C_plasma(t) is the plasma input function, C_blood(t) is the whole blood input function, RBC_binding(t) is the measured amount of tracer bound to red blood cells during the dynamic scan, and HCT is hematocrit.

Measurements of pig blood samples through the dynamic scan showed that the red blood cell binding was low (0%–5%) in the early phase of the input function, making it possible to use a population based value or to completely neglect this effect without introducing much error.

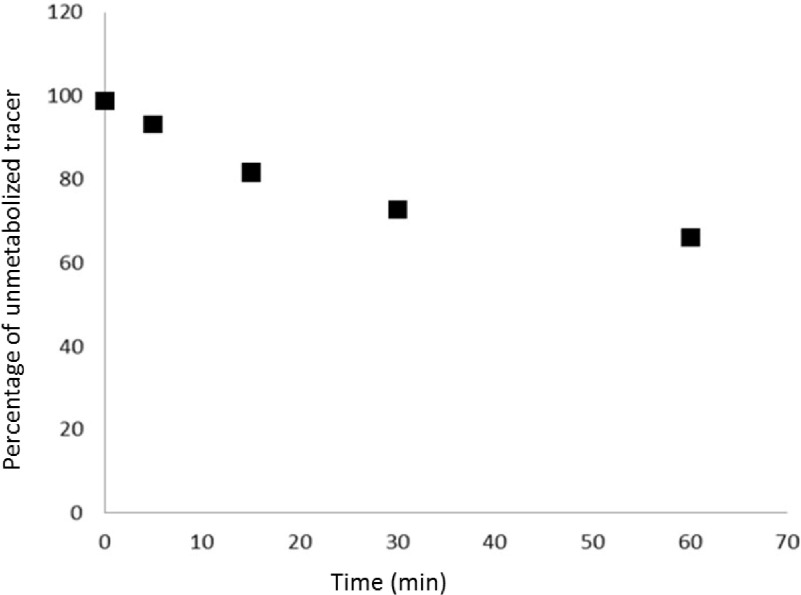
The input functions were corrected for metabolites which were determined by high pressure liquid chromatography (HPLC) of plasma samples³ (Fig. 3). Radioligand metabolism was slow with 80% unmetabolized tracer at 10 min.

FIG. 3.

The percentage of unmetabolized tracer over time for one individual pig study. The curves in other studies were similar in both shape and magnitude. The percentage of metabolized tracer in the first 3 min was relatively small, resulting in an insignificant change of the quantitation of ID-IF from metabolism.

2.G. Two-tissue parallel compartment model

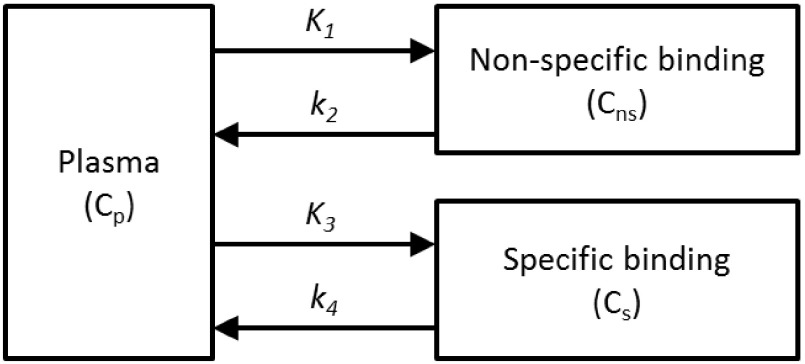
The kinetic parameters that quantify radioligand binding in the target organ were estimated by a compartmental model which included one plasma compartment for the input function and two compartments representing specific and nonspecific binding for the renal parenchyma. Using pig data from the biodistribution studies and the receptor distribution within the tissues, a two-tissue parallel connectivity model was chosen¹⁷ (Fig. 4). This was justified by the absence of a barrier between the receptor and plasma, which in brain tracer kinetic studies necessitates the use of a serial connectivity model. The parenchymal impulse response function of the parallel model is represented by a biexponential function,

$${\displaystyle f\left(t\right)=K_1{e}^{-k_{2}t}+K_3{e}^{-k_{4}t}.}$$ (5)

And the distribution volume ratio (DVR) can be calculated as

$${\displaystyle \text{DVR}=\frac{{\text{DV}}_{\text{specificbinding}}}{{\text{DV}}_{\text{non-specificbinding}}}=\frac{K_3}{k_4}/\frac{K_1}{k_2}.}$$ (6)

The integrated software package called kinetic imaging system (kis) (Ref. 18) was used to estimate the kinetic parameters from the renal cortical time activity curves using both the AD-IF and ID-IF.

FIG. 4.

A two-tissue parallel connectivity model to determine the biodistribution of angiotensin II subtype I receptor in the pig kidney.

3. RESULTS

3.A. Comparison between AD-IF and ID-IF

3.A.1. Effect of PET reconstruction (FBP vs OSEM) on the ID-IF

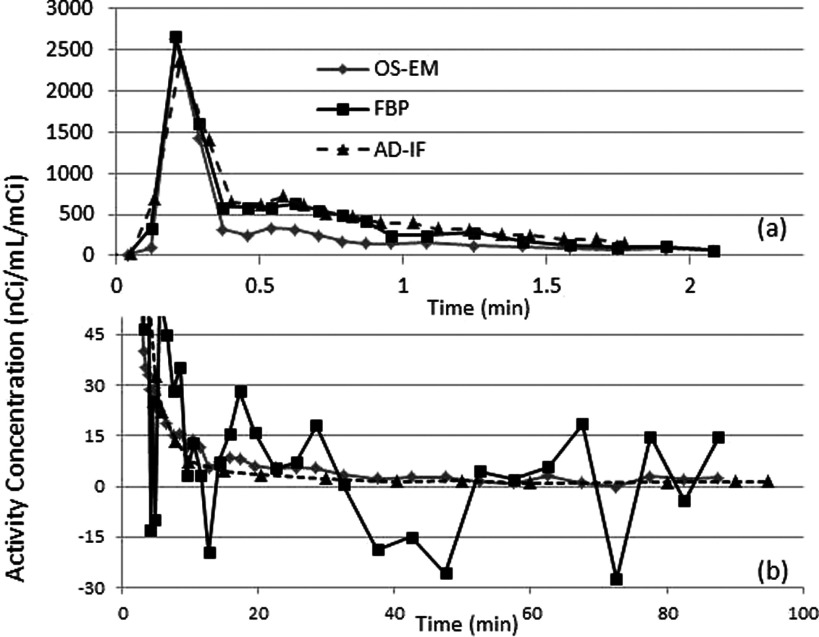
Figure 5 shows the ID-IFs acquired from the FBP and OS-EM reconstruction methods in the early (up to 2 min) and late phases of the dynamic PET study in a sample animal. Both ID-IFs were derived from the reconstructed images using identical VOIs with complete correction (partial volume correction, biological corrections). There were large differences between the input functions during the early phase between 0.5 and 2 min. As shown in Fig. 5(a), the ID-IF from FBP showed good agreement with AD-IF, while the ID-IF from OS-EM showed lower values between 0.5 and 2 min. This bias effect was reproducible in multiple pigs. During the later phase [Fig. 5(b)], the ID-IF obtained from FBP reconstruction is much noisier than the one obtained from OS-EM reconstruction, in line with other observations.^19,20

FIG. 5.

Comparison of ID-IF after correction using measurement from OS-EM reconstructed images and FBP reconstructed images and arterial blood samples derived input function (AD-IF) from a pig study. (a) The first 2 min. (b) After 3 min. This figure shows that FBP based ID-IF was a better choice at the early phase of input function with lower bias while OS-EM based ID-IF performs better at the late phase with lower noise. The correction includes PVC and biological corrections.

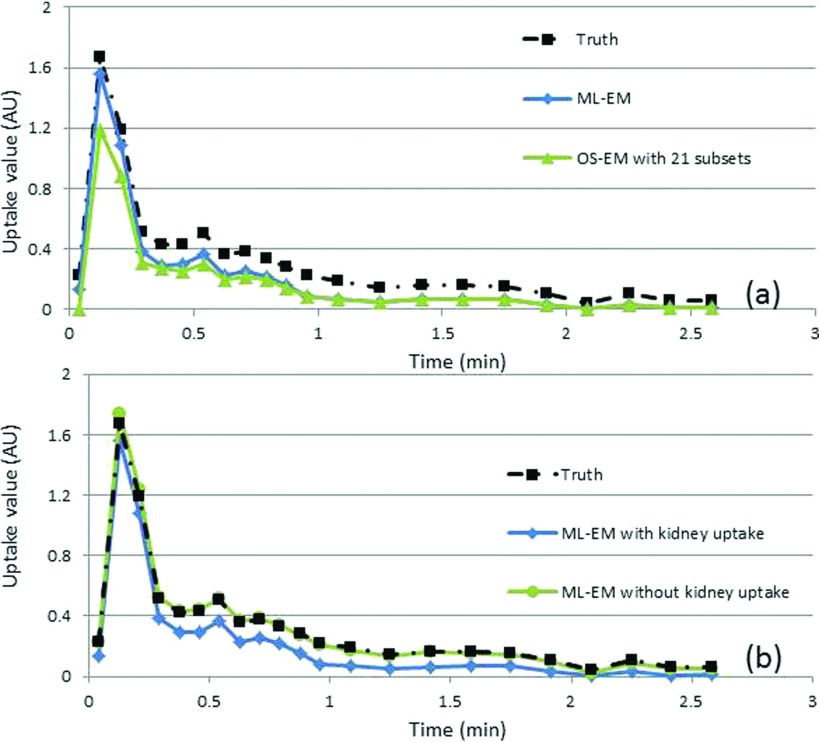
Results from a phantom study after averaging 100 noise realizations showed a bias similar to that from the iterative image reconstructions. Bias was observed in ∼0.5–2 min postinjection where the kidney has similar activities when compared with aorta. ML-EM showed less bias when compared with OS-EM, suggesting high number of subsets contributed to larger bias, which is consistent with literature.²¹ Bias was greatly reduced when the kidney uptakes were set to zero [Fig. 6(b)] suggesting that iterative image reconstruction produced bias in small structures (e.g., aorta) when there was a large structure (e.g., kidney) with a similar uptake value in the vicinity ∼0.5–2 min after injection [Fig. 2(b)]. The deviation of the average estimated value calculated from different noise realizations was much smaller and was likely not the main contributing factor to the bias. Both FBP image reconstruction results (averaging results of multiple noise realizations) and noise-free iterative image reconstruction were in good agreement with the ground truth from the phantom unlike the iterative image reconstruction results from noisy data. ML-EM resulted in smaller bias than OS-EM, suggesting that an increased number of subsets would further increase the bias. A study of different iteration number suggested that it takes about 100 updates for both OS-EM and ML-EM method to converge; thus, the bias in Fig. 6 is not caused by nonconvergence.

FIG. 6.

Comparison of the ID-IFs with the truth obtained from a dynamic digital phantom study and measured aorta activity level using (a) ML-EM and OS-EM image reconstruction methods with noise levels equivalent to those found clinically and (b) ML-EM using the digital phantom with and without kidney uptake.

With the combined use of FBP and OS-EM reconstruction, both bias and variance from the ID-IF of the pig data were reduced. The first 3 min of ID-IF were acquired from FBP reconstructed images, while the rest were acquired from OS-EM reconstructed images. The combined use of FBP and OS-EM for ID-IF resulted in good agreement with the data from the arterial blood samples.

3.A.2. Partial volume correction

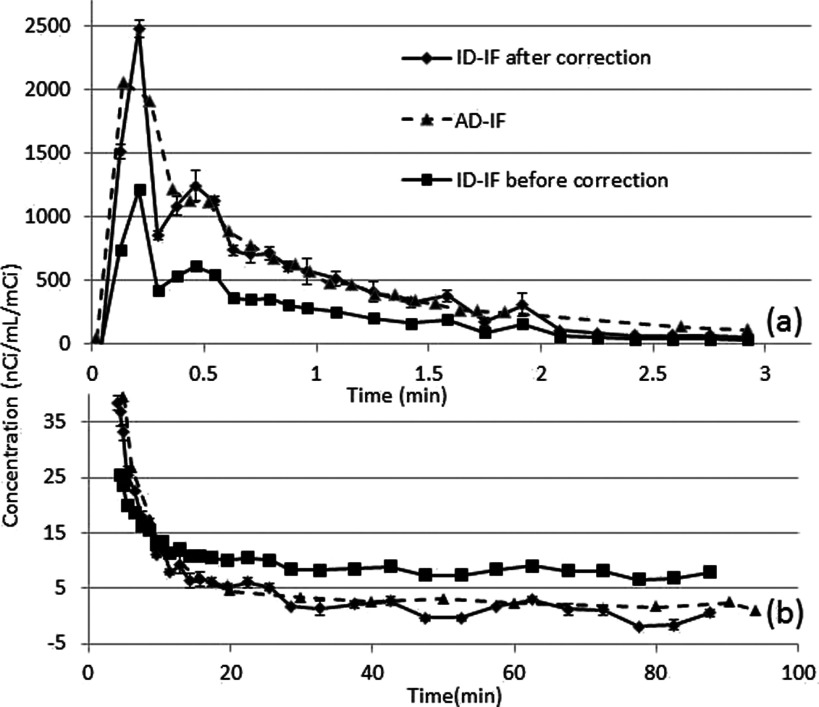
The AD-IF was used as the gold standard for the ID-IF. Figure 7(a) shows the ID-IF using combined OS-EM and FBP before and after partial volume correction, and the AD-IF study during the first 2 min postinjection. The uncorrected ID-IF is largely biased due to the spill-out effect, while the corrected ID-IF was well matched with the arterial blood samples. The AD-IF does not show a shape peak in the first minute due to the relatively long sampling period of 5 s. Similar results were observed in all experimental animals.

FIG. 7.

Comparison of ID-IF after correction, before correction, and AD-IF using a pig data. (a) The first 3 min (b) After 4 min. The corrected ID-IF shows good agreement with AD-IF. The correction includes PVC and biological corrections.

The area under the curve (AUC) was used for comparisons. Table II shows the AUC ratios for ID-IF and AD-IF after corrections for the first 3 min. The difference is around 5% for the last five studies and the average difference is 7.6%. The first 3 min contribute ∼80% of the total AUC.

TABLE II.

Ratio of AUC of ID-IF over AD-IF from pig studies.

Pig ID No.	1	2	3	4	5	6	7	8	9	Average
Ratio	1.16	1.06	0.83	0.92	1.06	0.96	1.02	0.94	1.06	1.00
Absolute difference	0.16	0.06	0.17	0.08	0.06	0.04	0.02	0.06	0.06	0.08

Figure 7(b) compares the corrected and uncorrected ID-IFs with AD-IF for the same pig study after 2 min. The uncorrected ID-IF has a significant bias compared to the AD-IF, which is caused by the spill-in effect from background activity. The ID-IF after correction matches well with AD-IF, albeit with a larger noise dependent variance. The difference between using a population based calibration point and an individual calibration point was small as the total contribution of the later phase is relatively small.

3.B. Kinetic parameter estimation

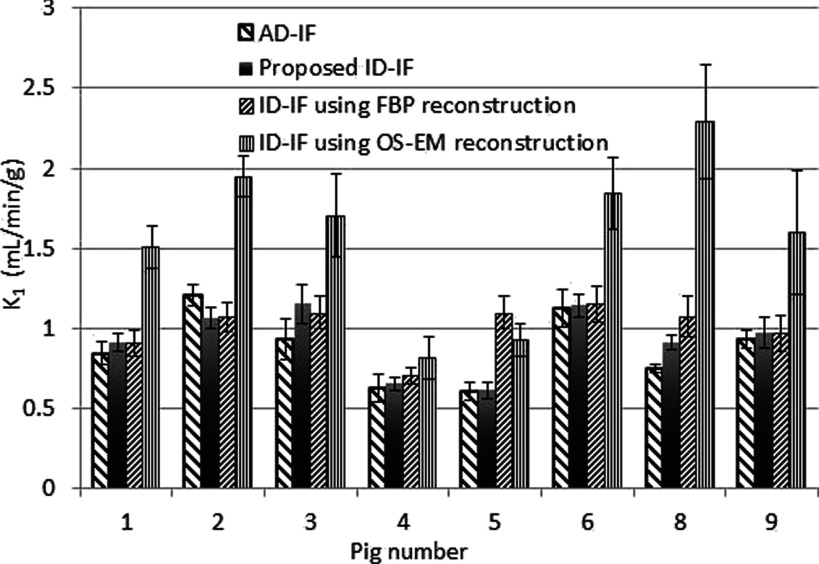
Using the 2-compartment model shown in Fig. 4, we were able to fit the pig kidney TAC and estimate the tracer kinetic parameters. Figure 8 shows the estimated K₁ values determined with four input functions: (1) AD-IF, (2) ID-IF with the proposed approach (e.g., using FBP at earlier time points and OSEM at later time points plus all other corrections), (3) ID-IF with FBP reconstruction plus all other corrections, and (4) ID-IF with OS-EM reconstruction plus all other corrections. The results show (Fig. 8) that the K₁ values determined with the proposed approach are the closest to the K₁ values determined with the AD-IF. These values also showed the highest linear correlation (R = 0.872). The reconstruction with FBP only resulted in a higher estimation error while OS-EM reconstruction resulted in much higher bias. Table III shows the estimated noise (calculated as the standard deviation of the estimation over the mean value of estimation) and the absolute percentage bias (defined as the absolute difference of kinetic parameters between AD-IF and ID-IF using different reconstruction methods over the value of kinetic parameters from AD-IF) of the kinetic parameters K₁, k₂, K₃, and k₄ from eight pig PET studies. (Time activity curves from pig number 7 were not analyzed due to a poor curve fit with the 2-tissue-compartmental model.)

FIG. 8.

The comparison of K₁ measured from AD-IF, the proposed ID-IF, ID-IF using only FBP image reconstruction, and ID-IF of using only OS-EM image reconstruction. The bias found in OS-EM results in a large difference compared to the gold standard (AD-IF).

TABLE III.

Average estimation errors of the parameters from eight pig PET studies.

	K1		k2		K3		k4
	[(ml/min)/g]		(1/min)		[(ml/min)/g]		(1/min)
Kinetic parameter	Absolute bias	Estimation noise	Absolute bias	Estimation noise	Absolute bias	Estimation noise	Absolute bias	Estimation noise
AD-IF	0	0.087	0	0.12	0	0.16	0	0.32
Proposed ID-IF	0.094	0.074	0.081	0.11	0.16	0.16	0.099	0.35
ID-IF using FBP reconstruction	0.22	0.095	0.17	0.16	0.32	0.41	0.45	0.63
ID-IF using OS-EM reconstruction	0.81	0.14	0.15	0.15	0.52	0.24	0.31	0.44

The results in Table III demonstrate that the difference between using the proposed ID-IF with correction and AD-IF is comparable within the estimation error and that the ID-IF is a feasible replacement for AD-IF. The use of FBP or OS-EM alone resulted in reduced accuracy (Fig. 8).

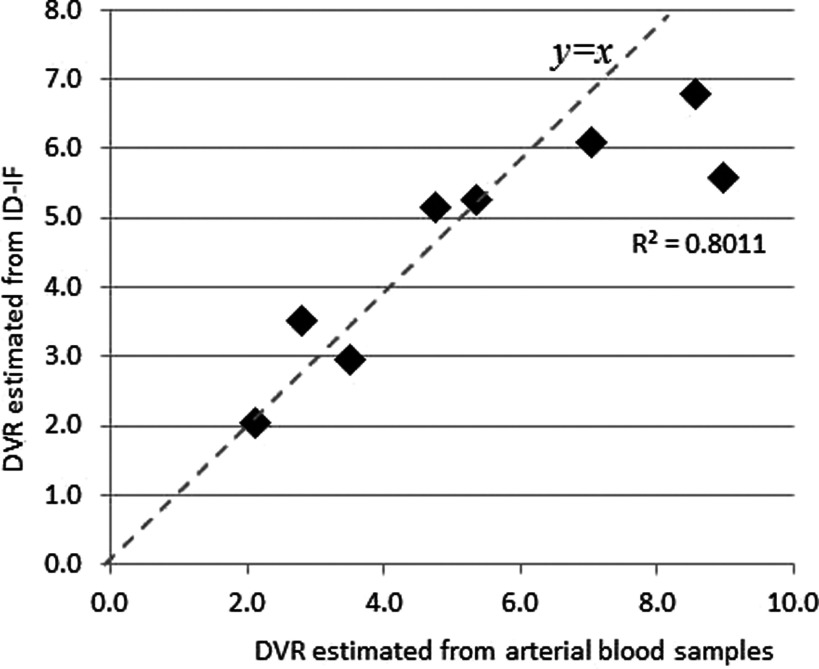
DV_{specificbinding} is defined as K₃/k₄ while DV_{non-specificbinding} is defined as K₁/k₂. In Fig. 9, the DVRs estimated from the ID-IF are plotted against those estimated from AD-IF in the eight pig studies. The correlation is 0.9489, showing that it is possible to use ID-IF to replace arterial blood samples.

FIG. 9.

The DVR estimated from ID-IF against those estimated from arterial blood samples from eight pig studies, with R = 0.872.

3.C. Acquisition time

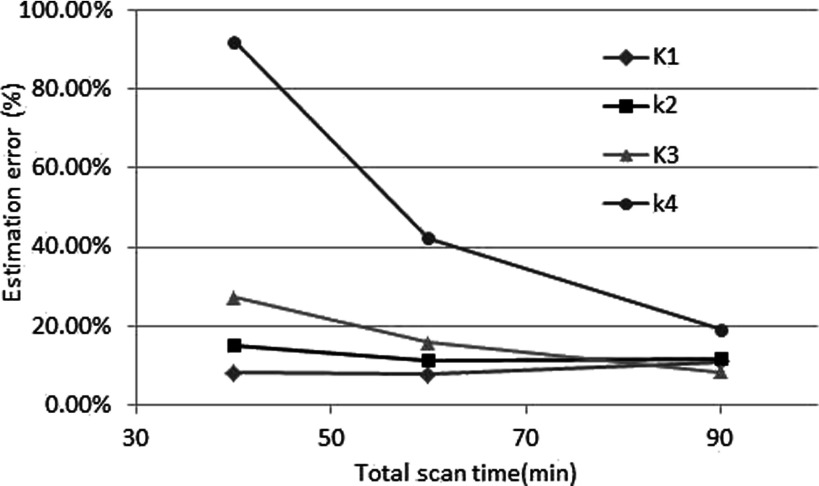
The effect of possible reduced scan time was also studied. The results are shown in Fig. 10. The estimation error of k₄ increases dramatically with a decrease in scan time less than 60 min since the information needed to estimate k₄ is mainly in the later phase. The changes in the estimation error of other parameters were relatively small.

FIG. 10.

The effects of total scan time for different parameters.

4. CONCLUSIONS AND DISCUSSIONS

In this study, the effects of different reconstruction methods on the ID-IF were investigated. Overall, reconstructed images from the FBP have a higher noise level but lower bias when compared to the OS-EM method. The combination of both (FBP for the first 2 min and OS-EM for the rest) can reduce both variance and bias for quantitative measurement in cases where only a small ROI can be used. Iterative image reconstruction methods such as OS-EM and ML-EM reconstructed images have lower noise levels even when the ROI is small.

Our results indicate that the quantification bias of OS-EM and ML-EM can be a problem when measuring activity in small anatomical structures such the aorta in the vicinity of larger anatomical structures such as the kidneys even after sufficient number of updates. The use of a larger ROI will reduce the variance, but it cannot reduce the bias, and quantitative measurements using iterative algorithms such as OS-EM and ML-EM should be handled with extra care. An easy solution to this problem is to use FBP reconstruction techniques with pre-reconstruction attenuation and scatter corrections. In cases where pre-reconstruction attenuation and scatter corrections are not available, work needs to be done to solve this problem.

Our studies using a digital phantom suggested that the quantitation bias of iterative reconstruction is related to the subset number used in OS-EM and the noise level. A reduced subset number will result in reduced bias, but the bias cannot be fully eliminated even with a minimal number of subsets (ML-EM). The bias is eliminated in a noise-free situation, which is not realistically available. The cause of the bias for the ML-EM algorithm can be explained using the update equation of expectation–maximization [Eq. (7)],

$${\displaystyle x_j^{l+1}=x_j^l\left[\frac{\sum _i\frac{p_i{K}_{i,j}}{\sum _{j^{\prime }}{K}_{i,j^{\prime }}\cdot x_{j^{\prime }}^l}}{\sum _i{K}_{i,j}}\right],}$$ (7)

where x_j is the density value in the j-th pixel, p_i is the collected projection data in bin i, and K_i,j is the projection matrix. l is iteration number. Unlike with FBP, the results of reconstruction using Eq. (7) are the result of multiple updates. Each update compares the original projection data to the calculated projection from the estimated image. In cases where a large anatomical structure such as the kidney has comparable uptake to that of the small target VOI, and when the contribution of the target VOI to the calculated projection data is comparable to the magnitude of the quantum noise in the projection data contributed from the large anatomical region, the update formula will likely be unable to distinguish the real activity uptake in the target VOI from the quantum noise. This causes the bias of the activity in the target VOI even after convergence. With current clinical setting (42 updates), it is likely that the insufficient updates number is another factor that contributes to higher bias in the OS-EM derived ID-IF. Unlike the formulation of ML-EM image reconstruction, FBP is strictly linear; the average of FBP reconstructed images each with noisy data is equivalent to the FBP image reconstruction of an averaged less noisy projection data. Therefore, ID-IF using FBP does not result in bias given all necessary corrections such as attenuation correction and PVC. The multiplicative update equation of the ML-EM does not enforce the linearity constraint, which may result in bias in high noise situations.

There are many ways to correct for the partial volume effect. In our case, as the anatomical structure and activity distribution are relatively simple, the estimation and application of the recovery coefficient is an effective method. For more complicated anatomical structures and distributions of activity, more advanced partial volume correction methods will be needed. Equation (2) is an approximation with the use of a single calibration point. The approximation was valid due to the fact that the slope of input functions in their later phase tends to be zero. The area under the input function after 10 min only contributes around 10% of the total area under the curve as observed in the AD-IF, and the effects of calibration point on the early phase are also negligible due to the large difference of magnitude in the early and late phases, indicating that the quantitative accuracy of the input function was less sensitive to the accuracy of the calibration point.

The DVR calculated using Eq. (6) is sensitive to the accuracy of kinetic parameters, as the error for each kinetic parameter propagated to the final estimation of DVR. A direct estimation approach should be applied in future studies to reduce estimation inaccuracy.

Although we did not detect any visible motion during the first 3 min of scanning in our pig studies, the acquired data might have been affected by motion of the animal during the 90-min scan time, even if the animals are tied to the bed. The small aorta VOI is very susceptible to motion effects. The use of a calibration point should make corrections possible for the spill-in and motion effects in the late phase of the dynamic study in future work.

Since the value of input function after 10 min is relatively small compared to the peak value, it is possible to use population based metabolite⁸ correction or no metabolite correction at all. The AUC difference between ID-IFs with and without was ∼2.7% on average, ∼6% at maximum, which is small. In this work, we applied both corrections for red cell binding and metabolites, but as indicated above, these corrections may not be necessary.

5. CONCLUSION

Our results show that with careful corrections and calibrations, the ID-IF derived from quantitative dynamic PET images using combined image reconstruction methods (FBP and OS-EM) can be used as the input function of the compartmental model to quantify the renal kinetics of ¹¹C-KR31173 both in experimental animals and can potentially be applied to humans.

Glossary

NOMENCLATURE

AD-IF=

artery derived input function

AT1R=

angiotensin II subtype 1 receptor

AUC=

area under curves

DVR=

distribution volume ratio

FBP=

filtered back projection

HCT=

hematocrit

HPLC=

high pressure liquid chromatography

ID-IF=

image-derived input function

kis=

kinetic imaging system

ML-EM=

maximum likelihood expectation maximization

MRA=

magnetic resonance angiography

OS-EM=

ordered subset expectation maximization

PET=

positron-emission tomography

PVE=

partial volume effect

PVC=

partial volume correction

RC=

recovery coefficient

ROI=

region of interest

TAC=

time activity curve

VOI=

volumes of interest