Table 1.

Large L scaling of some key quantities for RNA SSs. For the number of sequences Ω for the NS of the largest non-trivial structure, defined as Ω = 10^U, we find 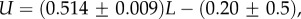whereas for the trivial structure, with Ω = 10^T, we find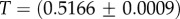 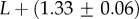so that U becomes relatively more close to T as L increases. The G-sampled mean of 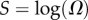scales as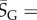 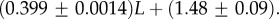For large L, 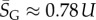, whereas for P-sampling 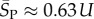so that 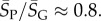Similarly, the standard deviations of log(Ω) can be directly calculated, and in the large L limit tend to 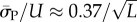and 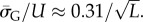This explains analytically what can be observed qualitatively in figure 3 and the electronic supplementary material, figures S1 and S2: the P_G(Ω) distribution is slightly narrower than the P_P(Ω) distribution. As L increases both distributions become more sharply peaked relative to the total range [0, U] and P_G(Ω) highlights SS phenotypes that are deeper into the tails of the P_P(Ω) distribution (and vice versa).

quantity	large L scaling form
total number of genotypes	NG = 4L
total number of SS phenotypes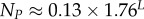
mean Ω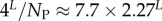
largest non-trivial Ω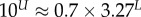
Ω for the trivial structure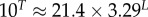
probability to sample trivial structure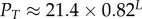
Ω near peak for phenotype sampling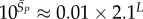
Ω near peak for genotype sampling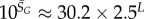
Shannon entropy of distribution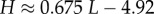
‘effective number’ of SS phenotypes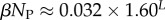
bias parameter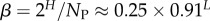
G-sampled mean number of stacks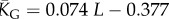
P-sampled mean number of stacks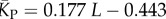