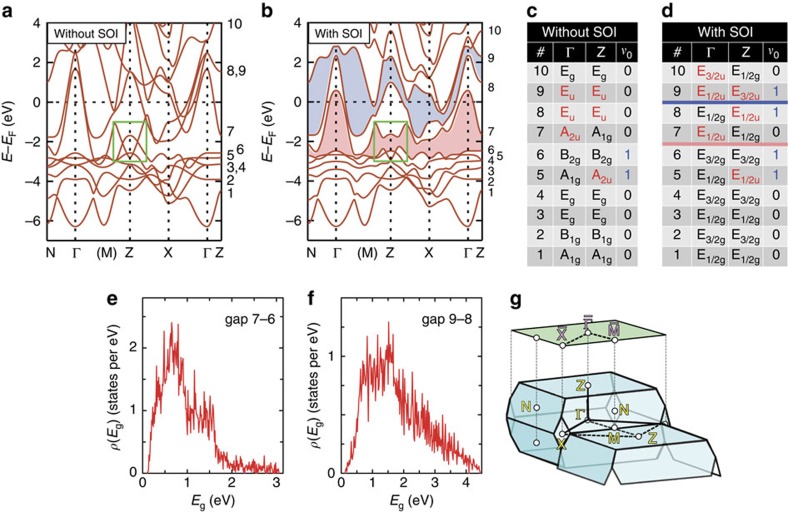
Figure 4. Analysis of parity and topological invariant for valence bands.
(a,b) First-principles band calculations without and with spin–orbit interaction (SOI), respectively. Valence bands are numbered by the energy (E) at the Z point, as shown in the right side of the panels. The green rectangles indicate the energy region where the surface Dirac cone appears. Pink (blue)-shaded area in b shows gap 7−6 (gap 9−8) induced by SOI. (c,d) Lists of the topological invariant ν0 and the symmetries of wavefunctions at the Γ and Z points without and with SOI, respectively. The left-end columns (#) indicate the number of the valence bands as given in a and b, respectively. The symmetries indicated with red (black) have the odd (even-) parity. ν0=1 indicates the topologically non-trivial band-inverted state. The pink (blue) line in d denotes the gap 7−6 (gap 9−8). (e,f) The distribution of the direct gap (Eg) for gap 7−6 and gap 9−8, respectively, obtained by the band calculation. (g) The blue solid (green plane) indicates the three (two)-dimensional Brillouin zone with high-symmetry points Γ, Z, N, X and M ( ,
,  and
and  ). Γ, Z, N and X are the three-dimensional time-reversal invariant momenta (TRIM).
). Γ, Z, N and X are the three-dimensional time-reversal invariant momenta (TRIM).