A phenomenological relative biological effectiveness (RBE) model for proton therapy based on all published in vitro cell survival data

Abstract

Purpose

Proton therapy treatments are currently planned and delivered using the assumption that the proton relative biological effectiveness (RBE) relative to photons is 1.1. This assumption ignores strong experimental evidence that suggests the RBE varies along the treatment field, i.e. with linear energy transfer (LET) and with tissue type. A recent review study collected over 70 experimental reports on proton RBE, providing a comprehensive dataset for predicting RBE for cell survival. Using this dataset we developed a model to predict proton RBE based on dose, LET and the ratio of the linear-quadratic model parameters for the reference radiation (α/β)_x, as the tissue specific parameter.

Methods and Materials

The relationship of the RBE on dose, dose average LET (LET_d) and (α/β)_x was explored using 287 experimental data points. A RBE model based on the linear quadratic model was derived from a nonlinear regression fitting to the data.

Results

The proposed model predicts that the RBE increases with increasing LET_d and decreases with increasing (α/β)_x. The model additionally predicts a decrease in RBE with increasing dose.

Conclusions

The proposed phenomenological RBE model is derived using the most comprehensive collection of proton RBE experimental data to date. The model agrees with previous theoretical predictions on the relationship between RBE, LET_d and (α/β)_x and also makes predictions on the relationship between RBE and dose. The proposed model shows a relationship between both α and β with LET_d. Previously published phenomenological models, based on a limited data set, may have to be revised.

1. Introduction

The relative biological effectiveness (RBE) is defined as the ratio of the reference photon dose to the proton dose necessary to cause the same level of effect. Traditionally, dose in proton radiotherapy is prescribed by scaling the physical proton dose by 1.1, i.e. protons are assumed to be 10% more efficient than photons. This however assumes a spatially invariant RBE within all treatment fields and disregards strong experimental evidence (mostly based on cell survival) that suggests the RBE varies. It has been suggested that using a variable RBE may help improve proton therapy outcomes as well as help interpret clinical results from proton therapy (Carabe et al 2013, Tilly et al 2005, Wedenberg and Toma-Dasu 2014, Paganetti 2015).

The RBE depends on the type of particle, the dose averaged linear energy transfer (LET_d) as a reasonable approximation of macroscopic dosimetric parameters, the cell or tissue type defined by (α/β)_x as well as the dose per fraction (Paganetti et al 2002). Previous experimental studies have shown a strong correlation between RBE and LET_d, suggesting RBE increases with increasing LET_d (Belli et al 1989, 1992, Folkard et al 1996, Perris et al 1986, Coutrakon et al 1997, Schettino et al 2001, Wouters et al 1996). This implies that the RBE around the distal edge of the spread out Bragg peak (SOBP) is larger than that in the plateau region since the increase in LET_d may soften the sharp decrease in dose at the distal edge. For this reason different studies have suggested a shift in the proton biological effective range by 1–2 mm (Robertson et al 1975, Paganetti and Goitein 2000). Generally, the RBE is expected to decrease with both increasing (α/β)_x and increasing dose (Paganetti et al 2002, Gerweck and Kozin 1999), however, the experimental data from single experiments is unsatisfactory in showing a clear correlation between RBE and (α/β)_x or dose. With the development of increasingly conformal proton therapy beam delivery systems, having a proper understanding of the RBE and the relevant treatment-scaling factor is essential for accurate calculation of the effective or biological dose in the patient as well as for efforts to reduce range margins.

A recent review study of the literature analyzed more than 70 reports to investigate the relationship of RBE with dose, biological endpoint and LET_d (Paganetti 2014), including a full analysis of RBE values for clonogenic cell survival. The analysis of the experimental data collected in this study suggested that the proton RBE increases with increasing LET_d as well as decreased with increasing (α/β)_x. It was also shown that the RBE increased with decreasing dose. The comprehensive collection of data in Paganetti (2014) provides an unprecedented platform for the development and/or refinement of a biophysical model that predicts proton RBE.

In this study the experimental data presented in Paganetti (2014) was extracted and analyzed to parameterize the relationship of RBE versus dose, LET_d and (α/β)_x for proton therapy. The derived model was compared with other published models. Note that, as in the review article, the LET_d values reported in this work are not absolute proton LET_d values but relative to the reference photon generated LET_d values (e.g. ~0.3 keV/μm for 6-MV photon beams).

2. Methods and Materials

2.1. Experimental Data

Paganetti (2014) extracted experimental data from 76 different studies and analyzed the data in the framework of the linear-quadratic (LQ) model. Allowing the calculation of common quantities for each of the studies and making it possible to determine certain parameters that the experiment may not have reported (e.g. RBE at a certain dose). In this study, the full collection of data presented in Paganetti (2014) was used to develop a new phenomenological model that predicts proton RBE. For each experimental data set, the following parameters relevant to the linear-quadratic model were extracted: α_x and β_x which describe the tissue dose response to photons, α and β describing the tissue dose response to protons and the dose averaged LET (LET_d) at the position of the biological sample. Since the LET_d value at the measurement point was not reported in the majority of the studies, Paganetti (2014) inferred the LET_d values in these cases from either look-up tables or Monte Carlo simulations. Assuming the same level of effect compared to the reference radiation, the RBE for different proton doses (D_p) was calculated using a RBE formalism based on the LQ model:

$$\mathit{RBE}\left[D_p,{\left(\frac{\alpha }{\beta }\right)}_x,{\mathit{LET}}_d\right]=\frac{1}{2D_p}\left(\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x^2+4{\left(\frac{\alpha }{\beta }\right)}_x\frac{\alpha [{\mathit{LET}}_d]}{{\alpha }_x}{D}_p+4\frac{\beta [{\mathit{LET}}_d]}{{\beta }_x}{D}_p^2}-{\left(\frac{\alpha }{\beta }\right)}_x\right).$$ (1)

The uncertainty in the RBE was calculated in Paganetti (2014) from the uncertainties reported in each of the individual published studies and used here to weigh the fitted data.

The primary data set extracted from Paganetti (2014) had a large range of LET_d and (α/β)_x values, resulting in RBE values ranging from 0.02 to 7.4 for a dose of 2 Gy. To develop a biophysical model relevant to clinical proton therapy, restrictions were applied to the primary data set. Only data points with LET_d < 20 keV/μm and (α/β)_x < 30 Gy were used in the fit. The exclusion criterion corresponds to the clinically relevant LET_d range, where the RBE is approximately linear with respect to LET_d (Paganetti 2014). These restrictions excluded 84 points from the original set of 369 data points. Data removed due to the restriction of (α/β)_x < 30 Gy included all the reported measurements in some studies (Ristic-Fira et al 2011, Petrović et al 2010, Antoccia et al 2009, Sakamoto et al 1980, Keta et al 2014) or the removal of selected data points (Belli et al 2000, Bettega et al 2000, Blomquist et al 1993, Grosse et al 2014, Baggio et al 2002, Schettino et al 2001, Urano et al 1980). The restriction of LET_d < 20 keV/μm excluded another two studies (Goodhead et al 1992, Wéra et al 2011) as well as selected data points from other studies (Belli et al 1989, 1992, 1993, 1998, 2000, Bettega et al 1998, Chaudhary et al 2014, Fiorini et al 2011, Folkard et al 1989, Ogheri et al 1997, Prise et al 1990, Schettino et al 2001, Schuff et al 2002, Sgura et al 2000). The RBE was considered for proton doses ranging from 1 – 10 Gy, governed by the assumed validity of the linear-quadratic model. For this reason, a data point only valid for doses between 8–24 Gy was also eliminated from the data set (Ristić-Fira et al 2008). Additionally, one outlier, with (α/β)_x = 25.5 Gy, LET_d = 12.1 keV/μm and RBE = 2.55 for D_p = 2 Gy, was excluded from the fit (Perris et al 1986). The other point reported in this study ((α/β)_x = 25.5, LETd = 5.8 and RBE = 1.62) was not an outlier but was also removed for the sake of consistency.

2.2 The RBE Model

A LQ-based RBE model (equation (1)) was used to parameterize the dependence of proton RBE on LET_d, (α/β)_x and dose:

$$\mathit{RBE}\left[D_p,{\left(\frac{\alpha }{\beta }\right)}_x,{\mathit{LET}}_d\right]=\frac{1}{2D_p}\left(\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x^2+4D_p{\left(\frac{\alpha }{\beta }\right)}_x{\mathit{RBE}}_{max}+4RB{E}_{\mathit{min}}^2{D}_p^2}-{\left(\frac{\alpha }{\beta }\right)}_x\right)$$ (2)

where RBE_max and RBE_min correspond to the asymptotic values of RBE at doses 0 and ∞ Gy, respectively (Carabe-Fernandez et al 2007). RBE_max and RBE_min are quantified in terms of the following ratios:

$$\begin{array}{c}{\mathit{RBE}}_{\mathit{max}}[\alpha ,{\alpha }_x,{\mathit{LET}}_d]=\frac{\alpha [{\mathit{LET}}_d]}{{\alpha }_x}\\ {\mathit{RBE}}_{\mathit{min}}[\beta ,{\beta }_x,{\mathit{LET}}_d]=\sqrt{\frac{\beta [{\mathit{LET}}_d]}{{\beta }_x}}.\end{array}$$ (3)

Carabe et al. (2012) assumed that both RBE_min and RBE_max have a linear relationship with respect to LET_d as well as a dependence on (α/β)_x. Here we make the same assumption for RBE_max however we assume that RBE_min has a dependence on $\sqrt{{(\alpha /\beta )}_x}$ (Jones 2015),

$$\begin{array}{c}{\mathit{RBE}}_{\mathit{max}}[{(\alpha /\beta )}_x,{\mathit{LET}}_d]=p_0+\frac{p_1}{{(\alpha /\beta )}_x}{\mathit{LET}}_d\\ {\mathit{RBE}}_{\mathit{min}}[{(\alpha /\beta )}_x,{\mathit{LET}}_d]=p_2+p_3\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x}{\mathit{LET}}_d,\end{array}$$ (4)

where p_0–3 are the fit parameters for our model. Both assumptions are in accordance with the LQ model. A fit to the extracted experimental data for the response parameter, RBE, was performed using a robust non-linear regression technique in Matlab (Mathwork Inc.) with predictor variables D_p, LET_d, and (α/β)_x with the model,

$$\mathit{RBE}\left[D_p,{\left(\frac{\alpha }{\beta }\right)}_x,{\mathit{LET}}_d\right]=\frac{1}{2D_p}\left(\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x^2+4D_p{\left(\frac{\alpha }{\beta }\right)}_x\left(p_0+\frac{p_1}{(\alpha /\beta )x}{\mathit{LET}}_d\right)+4D_p^2{\left(p_2+p_3\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x}{\mathit{LET}}_d\right)}^2}-{\left(\frac{\alpha }{\beta }\right)}_x\right).$$ (5)

The Matlab NonLinearModel.fit algorithm was used to estimate the fit coefficients (p_0–3) using an iterative procedure. The experimental data is associated with considerable uncertainties as a result of stochastic variations in the radiation fields as well as variations in cell sensitivity within the same culture. Furthermore, systematic differences in the analysis of the experimental data are likely to occur, which different groups may estimate differently. The uncertainties calculated for the RBE from Paganetti (2014) were used to weigh the data in the fitting procedure. No uncertainty in LET_d and dose were considered but the reported uncertainties in α_x, β_x, α and β were used to calculate the error in RBE.

2.3 Comparison of models

The fitted model was compared to two previously published proton RBE models, both based on a parameterization of the LQ RBE model. Each model has a different assumption regarding the relationship between LET, β, α and (α/β)_x. The Carabe et al. model (Carabe et al 2012) applies a linear relationship between RBE_min, RBE_max and LET_d with a slope depending on (α/β)_x (equation (2)) with

$$\begin{array}{c}{\mathit{RBE}}_{\mathit{max}}\left[{\mathit{LET}}_d,{\left(\frac{\alpha }{\beta }\right)}_x\right]=0.843+0.154\frac{2.686}{{(\alpha /\beta )}_x}{\mathit{LET}}_d\\ {\mathit{RBE}}_{\mathit{min}}\left[{\mathit{LET}}_d,{\left(\frac{\alpha }{\beta }\right)}_x\right]=1.09+0.006\frac{2.686}{{(\alpha /\beta )}_x}{\mathit{LET}}_d.\end{array}$$ (6)

The Wedenberg et al. model (Wedenberg et al 2013) on the other hand is based on the assumption that there is a linear relationship between α and LET_d with a slope depending on (α/β)_x, while β is assumed to be independent of LET_d with

$$\mathit{RBE}\left[D_p,{\left(\frac{\alpha }{\beta }\right)}_x,{\mathit{LET}}_d\right]=\frac{1}{2D_p}\left(\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x^2+4D_p\left({\left(\frac{\alpha }{\beta }\right)}_x+0.434{\mathit{LET}}_d\right)+4D_p^2}-{\left(\frac{\alpha }{\beta }\right)}_x\right).$$ (7)

Both models are based on fits through a small subset of the data used in our study.

2.4 SOBP and Patient RBE Simulation

A SOBP with a range/modulation width of 25 cm/10 cm was generated in water using the TOPAS Monte Carlo simulation system (Perl et al 2012), which has been extensively validated for proton therapy (Testa et al 2013). The SOBP was generated with a detailed model of the Francis H Burr Proton Therapy Center at Massachusetts General Hospital (Paganetti et al 2004). TOPAS features a number of different scorers, a function called by the user to record a specific simulation property. Both dose and LET distribution scorers were used in the simulation with a step size of 1 mm. The dose and LET_d along the SOBP was scored and used to calculate the RBE with the three models described above.

TOPAS has previously been used to simulate both LET (Giantsoudi et al 2013, Sethi et al 2014, Grassberger et al 2011) and RBE distributions (Polster et al 2015) in patient environments. For this study, two patients were selected from the MGH clinical patient database, a pediatric head and neck patient as well as a prostate patient. The purpose was to demonstrate the clinical impact predicted by our model for targets with low (α/β)_x (e.g. the prostate) and for treatment sites adjacent to organs at risk (e.g. the brainstem). An in-house Matlab-based script that links the treatment planning system to TOPAS was used to create all the input files for the simulation. The simulations were performed using the same steps as described elsewhere (Paganetti et al 2008, Schuemann et al 2014, Schümann et al 2012). All simulations were performed on a research-computing cluster with 10 and 30 parallel simulations per SOBP and patient field, respectively, each with 250,000 protons starting at the entrance of the treatment head. Variance reduction techniques were employed increasing the statistical accuracy by a factor of 64 (Ramos-Méndez et al 2013). The fitted RBE model was implemented in TOPAS as a new extension and then used to simulate the RBE distributions in each patient case. Our goal was not to do a study on the clinical impact of RBE variations but rather show the use of the RBE model in a patient.

3. Results and Discussion

3.1 Fit Parameters

We found that the fitted model (Equation (4)) would extend to the complex plane when data points with (α/β)_x ~ 0 were included in the fit. In order to avoid this behavior, three additional data points were removed from the primary data set. Two of these points had α_x = 0 Gy (Green et al 2001). The other point had (α/β)_x = 6.2 ×10⁻¹³ Gy (Hall et al 1978). The values of the fit coefficients in Equation (6) that best fit the experimental data, including the above mentioned restrictions, was found to be: p₀ = 0.99064 (Standard Error (SE) 0.014125), p₁ = 0.35605 (SE 0.015038), p₂ = 1.1012 (SE 0.0059972) and p₃ = −0.0038703 (SE 0.00091303) with a R-squared value of 0.255. From equation (4) we find,

$$\mathit{RBE}\left[D_p,{\left(\frac{\alpha }{\beta }\right)}_x,{\mathit{LET}}_d\right]=\frac{1}{2D_p}\left(\sqrt{{\left(\frac{\alpha }{\beta }\right)}_x^2+4D_p{\left(\frac{\alpha }{\beta }\right)}_x\left(0.999064+\frac{0.35605}{{(\alpha /\beta )}_x}{\mathit{LET}}_d\right)+4D_p^2{\left(1.1012-0.0038703\sqrt{{(\alpha /\beta )}_x}{\mathit{LET}}_d\right)}^2-{\left(\frac{\alpha }{\beta }\right)}_x}\right)$$ (7)

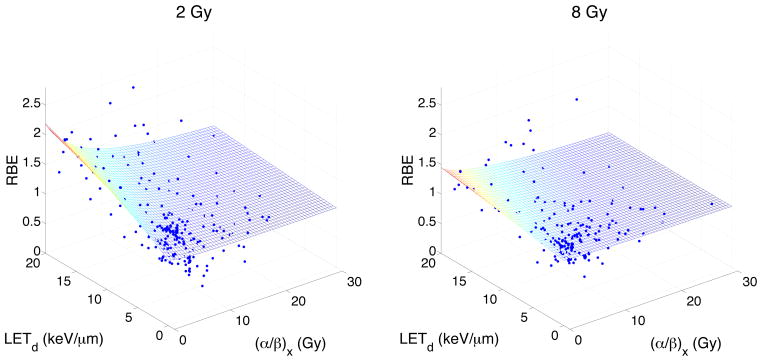
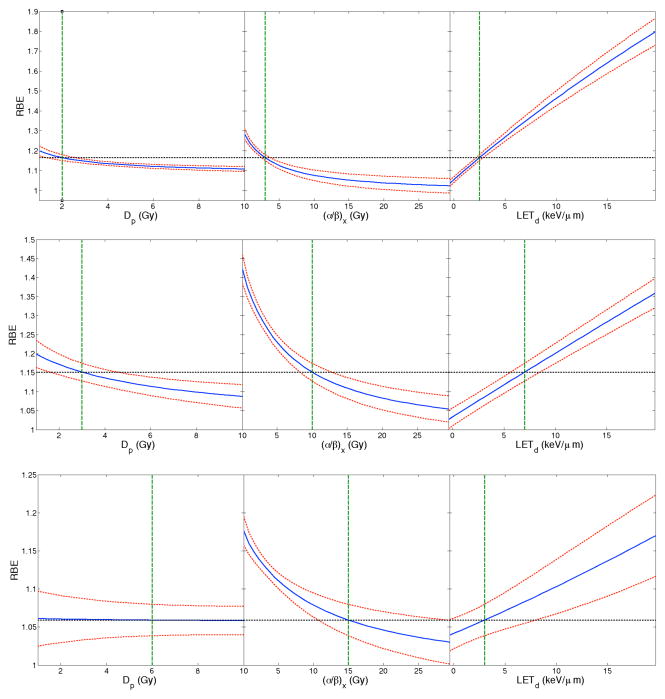
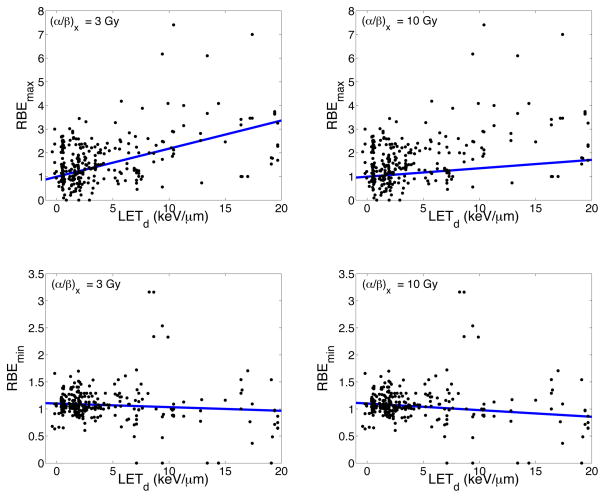
Figure 1 shows the dependence of the RBE for cell survival on LET_d and (α/β)_x for a dose of 2 Gy (left panel) and 8 Gy (right panel) as predicted by our model. The experimental data used in the fit is also shown. The model predicts a decrease in RBE with increasing (α/β)_x and an increase in RBE with increasing LET_d. As the dose increases, the model plane flattens and the RBE decreases. Figure 2 shows slices through the regression surface of our predicted model and plots the change in the response variable (D_p, (α/β)_x or LET_d) as a function of RBE, when all other predictor values are constant. The red dashed curves show the 95% confidence bounds for the predicted response values. Figure 3 plots the predicted RBE_max and RBE_min for our model as a function of LET_d for two different values of (α/β)_x. The experimental data is also plotted.

Figure 1.

The RBE for cell survival as a function of LET_d and (α/β)_x for a dose of 2 Gy (left panel) and 8 Gy (right panel) as predicted by our model. The experimental data used in the fit is also plotted. The LET_d is given relative to the reference photon radiation.

Figure 2.

Slices through the regression surface of our predicted model. The blue line in each row shows the change in the parameters (D_p, (α/β)_x or LET_d) as a function of RBE when all other predictors are held constant. The horizontal dashed black line in each panel shows the predicted RBE for the specific values of the predictor variables corresponding to the dashed vertical green lines. The red curves in each panel show the 95% simultaneous confidence bounds for the predicted response values. The top panel represents the case where D_p = 2 Gy, (α/β)_x = 3 Gy and LET_d = 2.5 keV/μm, the middle row where D_p = 3 Gy, (α/β)_x = 15 Gy and LET_d = 7 keV/μm and the bottom row where D_p = 6 Gy, (α/β)_x = 15 Gy and LET_d = 3 keV/μm.

Figure 3.

RBE_max and RBE_min as predicted by our model as a function of LET_d for an (α/β)_x of 3 and 10 Gy. The experimental data is also included in the plots.

3.2 Model Comparison

RBE as a function of LET

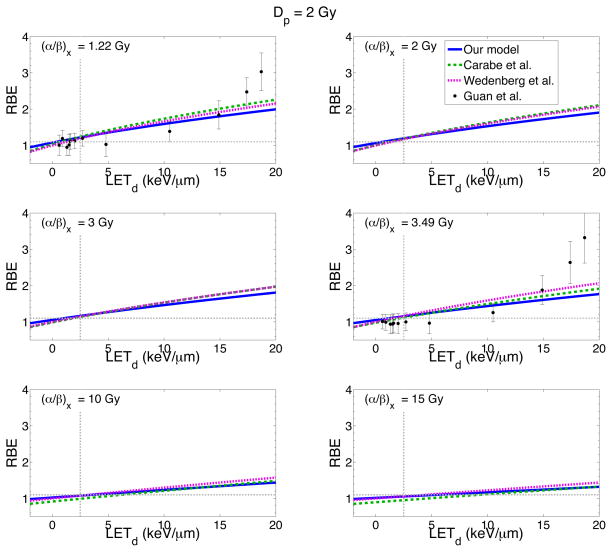
Figure 4 plots the RBE as a function of LET_d predicted by three different biological models for different (α/β)_x values and for a dose of 2 Gy. The horizontal grey dashed line represents a constant RBE of 1.1 and the vertical line a LET_d of 2.5 keV/μm (~ average LET_d in the plateau region of the SOBP). For each of the models considered, the RBE increases with increasing LET_d with a somewhat linear relationship between RBE and LET_d (especially at large (α/β)_x). All models predict a positive slope of RBE as a function of LET_d, with a steeper slope occurring at low (α/β)_x. This agrees with other theoretical studies which also find a linear relationship between RBE and LET_d, in the clinically relevant range of LET_d (Wilkens and Oelfke 2004, Chen and Ahmad 2012).

Figure 4.

RBE for cell survival as a function of LET_d for six different (α/β)_x values and a dose of 2 Gy. Three different models predict the RBE: our model (blue solid line), the Carabe et al. model (green dashed line) and the Wedenberg et al. model (pink dotted line). To test the predictability of the models, recently published experimental data for two different (α/β)_x values is also included (Guan et al. 2015).

At low (α/β)_x values (less than ~5 Gy), our model predicts RBE values lower than the Carabe et al. and Wedenberg et al. models for LET_d ≳ 5 keV/μm. At an (α/β)_x of 1.22 Gy our model is ~8% lower than the Wedenberg et al. model and ~13% lower than Carabe et al. model for LET_d > 5 keV/μm. Our model however predicts slightly higher RBE values at LET_d ≲ 5 keV/μm. For high (α/β)_x values (≥ 10 Gy), our model agrees better with the Wedenberg et al. model for low LET_d values. However at high LET_d, our model is similar to the Carabe et al. model. The discrepancy most likely reflects the limited data selected for the fits in both the Wedenberg et al. and Carabe et al models.

To test the predictability of our model, we also include new experimental data on RBE as a function of LET_d (Guan et al 2015) for an (α/β)_x of 1.22 Gy and 3.49 Gy, published after Paganetti (2014). The reported α, β, α_x, β_x and LET_d were extracted from the study and the RBE for 2 Gy was calculated for each data point. At low LET_d, most of the experimental data points fall in the region where all three of the models agree relatively well (within ~4%). At higher LET_d values, the experimental data agrees better with our model, within the uncertainties of the experiment. However the experimental data at very high LET_d values (LET_d = 18.7 kev/μm) show RBE values much higher than those predicted by any of the three models. One reason for this discrepancy could be due to the assumption in all of the models that α and β are linear functions of LET_d, whereas this experimental data seems to suggest an increase in slope as LET_d increases. This behavior is however not supported by our fit through all the experimental data.

RBE as a function of (α/β)_x

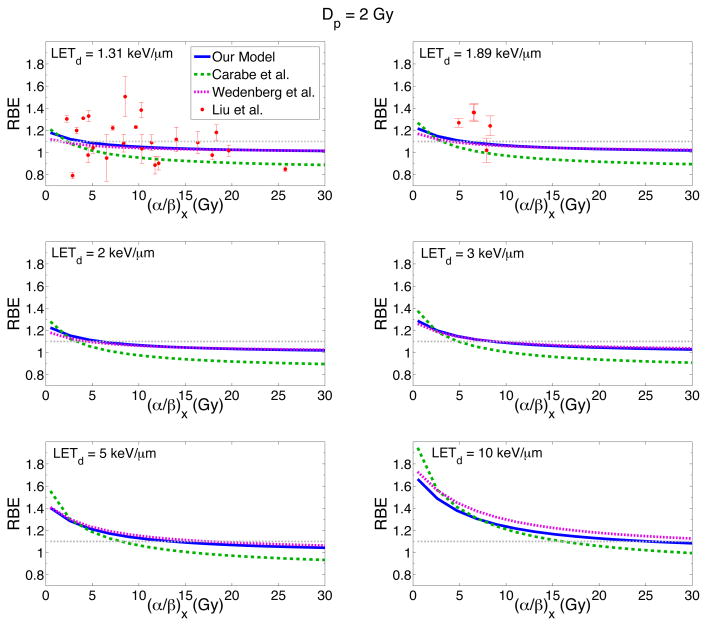
Figure 5 shows the RBE for cell survival as a function of (α/β)_x for four different LET_d values and for a dose of 2 Gy, predicted with the same models as Figure 4. The RBE decreases with increasing (α/β)_x for all three models. The decrease in RBE with increasing (α/β)_x is most significant at low (α/β)_x values, especially at large LET_d values, where the model curves are steeper.

Figure 5.

RBE for cell survival as a function of (α/β)_x for six different LET_d values and a dose of 2 Gy. Three different models predict the RBE: our model (blue solid line), the Carabe et al. model (green dashed line) and the Wedenberg et al. model (pink dotted line). To test the predictability of the models, recently published experimental data for LET_d values of 1.31 and 1.89 keV/μm is also included (Liu et al. 2015).

Our model has closer agreement with the Wedenberg et al. model, especially at low LET_d values (≤ 5 keV/μm). The Carabe et al. model predicts higher RBE values at low (α/β)_x values (< 2 Gy) than both other models but predicts much lower RBE values for (α/β)_x values greater than ~5 Gy (up to 14% less in the case of LET_d = 2 keV/μm).

In order to assess the predictive power of the model, experimental data published after the 2014 review (Paganetti 2014) are also shown in figure 5. The data were obtained in vitro using lung cancer cell lines for a LET_d of 1.31 and 1.89 keV/μm, relative to the reference photon radiation (Liu et al 2015). At a LET_d of 1.31 keV/μm, the majority of the experimental data predicts RBE values less than ~1.1. The experimental data however doesn’t favor one particular model. At a LET_d of 1.89 keV/μm, most of the RBE data values are larger than 1.1, which all three models underestimate. The large spread in the experimental data demonstrates not only the challenge in measuring RBE but also the difficulty in determining an effective model from this data.

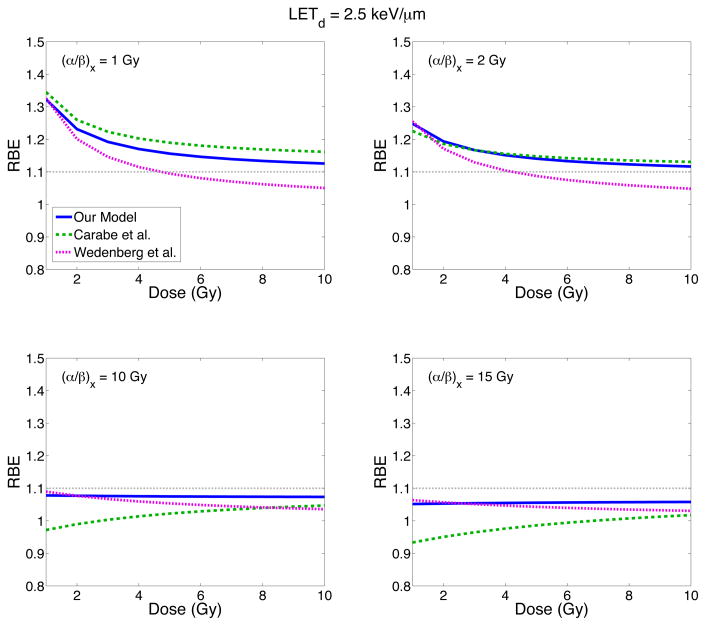
RBE as a function of dose

Figure 6 shows the RBE for cell survival as a function of dose for different (α/β)_x values and for an LET_d of 2.5 keV/μm. The LET_d was chosen as an approximate value of the LET_d in the plateau region of a SOBP (~2–3 keV/μm). The RBE decreases with increasing dose for (α/β)_x ≤ 2 Gy for all models. For large (α/β)_x, the RBE in the Carabe et al. model increases with increasing dose. The Wedenberg et al. model however predicts a decrease in RBE with increasing dose for all (α/β)_x values considered. For high (α/β)_x, the slope of our model converges to zero with RBE ~ 1.08 and 1.05 for (α/β)_x = 10 and 15 Gy, respectively.

Figure 6.

The RBE as a function of dose for different (α/β)_x values. Three different models predict the RBE: our model (blue solid line), the Carabe et al. model (green dashed line) and the Wedenberg et al. model (pink dotted line).

Most experiments predict an increase of RBE as dose decreases, however some experimental data indicate the opposite behavior (Paganetti 2014). Overall, the fitted model has better agreement with the Carabe et al. model at low (α/β)_x, predicting RBE values ~7% higher than the Wedenberg et al. model for (α/β)_x = 2 Gy. However at high (α/β)_x, the fitted model predicts RBE values up to ~11% higher than the Carabe et al. model.

In the Carabe et al. models, the trend of increasing RBE with increasing dose is due to the fact that RBE_min (RBE as D → ∞ Gy) is larger than RBE_max (RBE as D → 0 Gy) for high (α/β)_x values (and low LET_d values). This trend is not observed in some other models which predict a decrease in RBE for increasing dose for all (α/β)_x and LET_d values (Wedenberg et al 2013, Elsässer et al 2010, Wilkens and Oelfke 2004, Jones 2015). This is discussed further in (Grün et al 2013). An increase of RBE with dose is also not observed in our model.

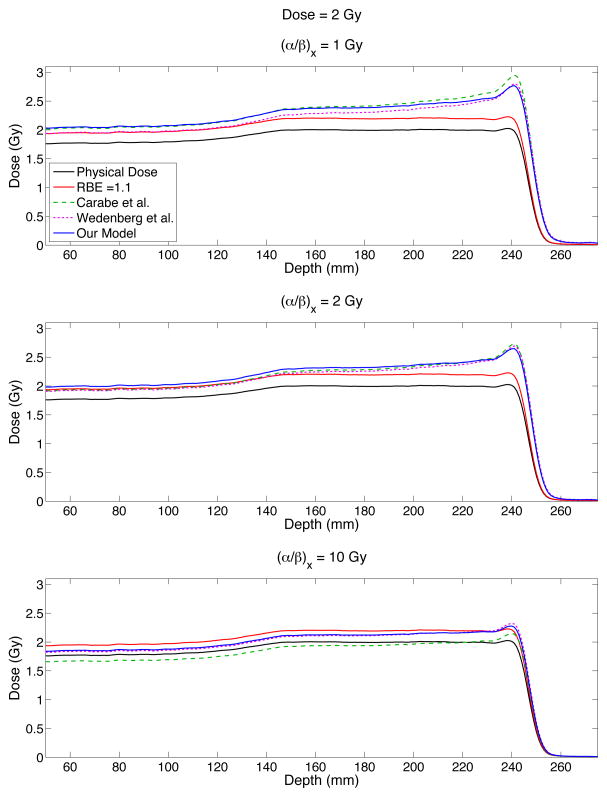
Spread out Bragg Peak (SOBP) simulation

The RBE values calculated by our, Wedenberg et al. and Carabe et al. models using the LET_d and dose values of the simulated SOBP are shown in Figure 7. The simulated SOBP had a modulation width of 10 cm and range of 25 cm with an average LET_d of ~ 3 keV/μm in the plateau region of the SOBP. The LET_d in the middle of the plateau region of the SOBP (depth ~160 – 220 cm) ranged from 1.4 – 3.1 keV/μm and from ~1.4 – 10 keV/μm over the entire plateau region.

Figure 7.

Predicted biological doses for three different models: Carabe et al. model (green dashed curve), the Wedenberg et al. model (pink dotted curve) and our model (blue solid curve) for a simulated spread out Bragg peak (SOBP) with a modulation width of 10 cm and a range of 25 cm. The physical dose is shown by the black solid curve while the red curve shows the physical dose scaled by a constant value of 1.1.

Each of the considered RBE models predict an increase in the biological dose at the distal edge of the SOBP as a result of the increase in LET_d (~7 keV/μm at 90% dose in the distal falloff) combined with a sharp drop in dose. At (α/β)_x = 1 Gy, the Carabe et al. model predicts the highest biological dose in the SOBP. At 90% dose in the distal falloff, the Carabe et al. model predicts a biological dose ~9% higher than our model. At the same point in the distal falloff, our model has a biological dose 28% higher than the dose scaled by 1.1, which is generally used in clinical treatment planning. The three models have the best agreement at an (α/β)_x of 2 Gy, especially in the plateau region of the SOBP. At 90% dose in the distal falloff, the Carabe at al. and Wedenberg et al. models both predict ~5% more biological dose than our model.

At an (α/β)_x value of 10 Gy, our model and the Wedenberg et al. model closely agree within ~1–2%, predicting RBE values between the physical and constant biological dose. At the distal edge, both models predict RBE values slightly larger than the constant RBE = 1.1 case (~4% higher). The Carabe et al. model predicts values lower than the physical dose in these regions except for at the distal edge, where the Carabe et al model is approximately equal to the constant biological dose. This is a result of the Carabe et al. model predicting RBE values below 1.0 for low LET_d values (see Figure 5).

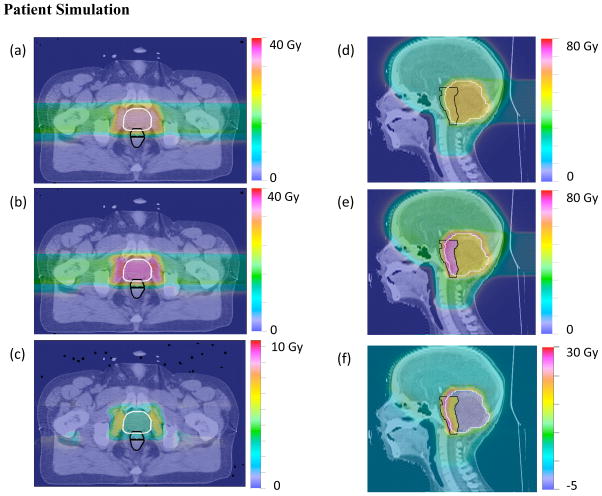
Two different proton treatment plans were simulated; a prostate and pediatric head and neck case, to demonstrate the RBE model predictions in a patient. The prostate case consisted of two transverse beams. We assume a prostate (α/β)_x value of 1.5 Gy with α_x = 0.036 Gy⁻¹ and β_x = 0.024 Gy⁻² (Brenner and Hall 1999). The rectum as well as the surrounding tissue (α/β)_x value was set to 3.1 Gy with α_x = 0.0890 Gy⁻¹ and β_x = 0.0287 Gy⁻² (Terry and Denekamp 1984). The head and neck treatment plan consisted of 10 beams. The (α/β)_x value of the target volume was set to 11 Gy with α_x = 0.55 Gy⁻¹ and β_x = 0.019 Gy⁻² (Steele et al. 1991). The (α/β)_x value of the rest of the brain was set to 2.1 Gy with α_x = 0.0499 Gy⁻¹ and β_x = 0.0238 Gy⁻² (Meeks et al 2000). For each case, the different (α/β)_x values were assigned to the relevant contours in the patient plan (e.g. 1.5 Gy to the prostate PTV and 3.1 Gy to all others). The left and right panels of figure 8 show both the prostate and the head and neck cases, combining all treatment fields for a total prescribed dose of 1.8 Gy per fraction. The biological dose with RBE assumed to be 1.1 is shown in (a) and (d) for each case. The biological dose with the RBE calculated from the proposed model is shown in (b) and (e) for each case. The difference between the biological dose with constant RBE and that calculated with the proposed model is shown in (c) and (f).

Figure 8.

Patient simulation studies of prostate (left panel) and head and neck (right panel) proton treatments. The biological dose with a constant RBE of 1.1 is plotted in (a) and (d) for the prostate and head and neck cases, respectively. The prescribed dose for the head and neck case was 55 Gy, while that for the prostate case was 35 Gy. The biological dose calculated with our proposed model is plotted in (b) and (e) for each case. The plots in (c) and (f) show the difference in biological dose between the RBE = 1.1 and the proposed model cases. The PTV is shown in white in both cases, while the rectum and brain stem (sensitive critical structures) are shown in black for each respective case.

In the case of the prostate treatment plan, two beams are delivered transversely and the distal edges of each SOBP have a higher RBE value than that of the plateau region of the SOBP. The plateau region coincides with the primary target volume (PTV). In this case, the areas that receive a higher biological dose as predicted by our model do not coincide with any critical structure (e.g. the rectum, represented by the black contour). The elevated RBE is mainly driven by the low value of the (α/β)_x value in the prostate. The actual RBE values calculated within the prostate target were ~1.2, while the RBE values occurring in the regions adjacent to the target region were ~1.3, instead of the assumed constant RBE of 1.1. Thus, the prescribed dose to the target would be exceeded by ~9% based on our model calculations, which could impact the interpretation of clinical trials comparing tumor control for proton versus photon therapy.

In the case of the head and neck treatment plan, the proposed model predicts that the region just outside the target volume receives a biological dose significantly higher than assumed by the current clinical practice using an RBE of 1.1. In this particular case, this region does coincide with a critical structure, the brainstem. The RBE values within the target were ~1.1 but those occurring within the sensitive brainstem were ~36% higher (RBE ~ 1.5). It has been suggested that in cases where proton fields stop in the brainstem, elevated RBE values could lead to brainstem toxicity. A recent study did not find statistically significant evidence to support this claim (Giantsoudi et al. 2015).

Figure 8 is shown to demonstrate how the use of our model might impact the RBE-weighted dose in proton therapy. Since this paper focuses on the model parameterization, an extended discussion about the clinical impact is beyond the scope of the manuscript. Note that the majority of published RBE values are based on clonogenic cell survival in vitro, which sheds some light on RBE variations in patients with respect to tumor control probability (TCP). Our model, as well as the majority of models previously published is based on clonogenic cell survival. The relevance of this data to define an RBE for normal tissue complications probabilities (NTCP) is controversial (Paganetti 2014, 2015). Due to lack of sufficient experimental data, RBE variations deduced from cell survival data may have to be considered not only for TCP but also for NTCP considerations.

Conclusion

We present a phenomenological model based on the well-know LQ model, to determine proton RBE as a function of dose averaged LET, the tissue specific (α/β)_x parameter and dose. Our model makes the assumptions of an inverse linear relationship of RBE_max to (α/β)_x and a linear relationship of RBE_min to $\sqrt{{(\alpha /\beta )}_x}$ as supported by the LQ model.

The model was derived using a non-linear regression fit to all published RBE experimental measurements before September 2014. The fitted model incorporates experimental data from a range of different (α/β)_x values (cell lines) as well as LET values for different doses, simultaneously. All previously published phenomenological models were based on limited experimental data sets.

The proposed model predicts an increase in RBE with increasing LET_d and a decrease in RBE with increasing in (α/β)_x. These relationships agree with observations from previous studies and with other theoretical predictions (Wedenberg et al 2013, Carabe et al 2012). The proposed model predicts a dose dependence on the RBE that depends on the LET_d and (α/β)_x values. For low (α/β)_x values, the RBE decreases with increasing dose. However for low LET_d and high (α/β)_x values, the RBE has very little dependence on dose. The proposed model assumes a linear relationship between α and LET_d as well as between β and LET_d. Some other models predict a constant β (β = β_x) (Wedenberg et al 2013, Chen and Ahmad 2012, Wilkens and Oelfke 2004), while the model by Carabe et al. uses a linear relationship between RBE_min and LET_d with a positive slope dependent on the inverse of (α/β)_x. Our model predicts a linear relationship between RBE_min and LET_d but with a small negative slope dependent on the square root of (α/β)_x.

The proposed model predicts the RBE for cell survival and is thus not necessarily applicable to other endpoints. While our model suffers from considerable uncertainties due to the spread of the underlying data, it can serve as a guideline when comparing proton and photon therapy results on tumor control and toxicities. The implications of experimental RBE values for tumor control probabilities and normal tissue complication probabilities have been discussed elsewhere (Paganetti 2014).