Figure 1.

Detection Mechanisms and Integration Criteria

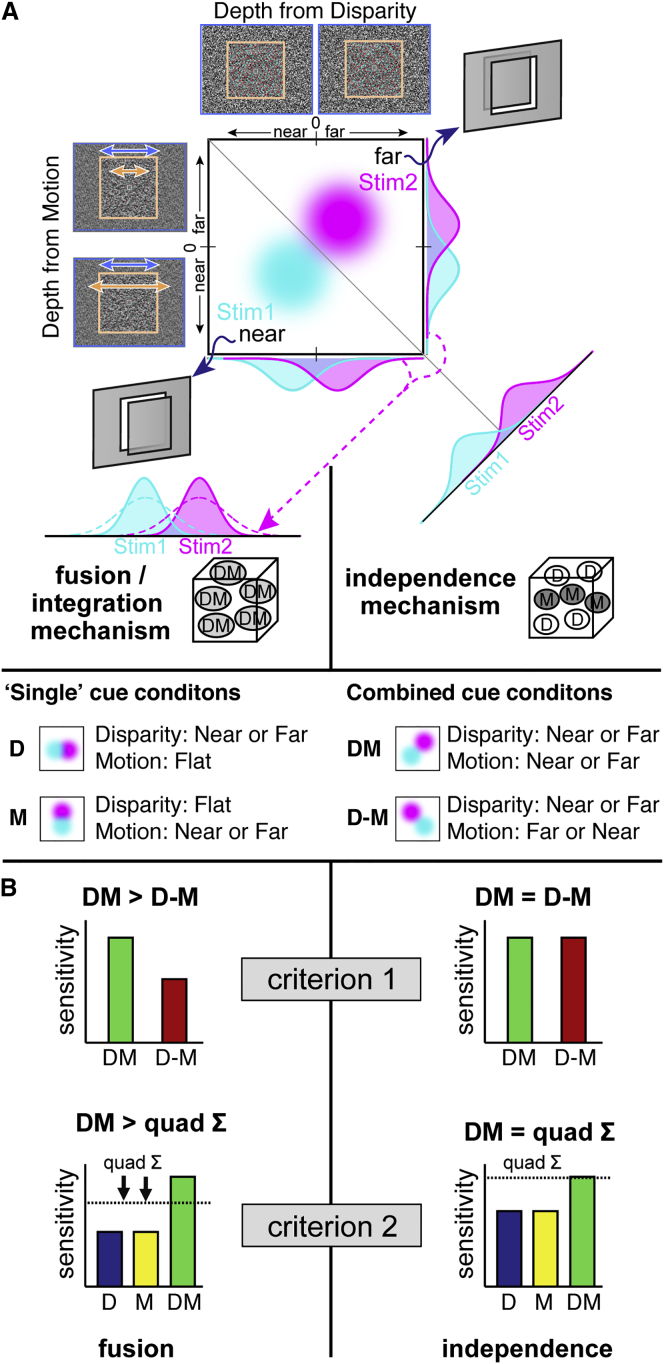
(A) Near versus far depths defined by motion and disparity. We illustrate depth estimators for stimulus 1 versus 2 as bivariate Gaussian distributions (magenta versus cyan “blobs”) in this motion-disparity space. A fusion mechanism (left) combines the cue dimensions to reduce variance: averaged estimator distributions become more “peaked” and are thus more discriminable. By contrast, an independence mechanism (right) increases the effective separation between the stimuli: by Pythagoras’ theorem (quadratic sum), the peak-to-peak separation between stimulus 1 and 2 is greater along the hypotenuse. Experimentally, we draw stimuli from different regions of the disparity-motion space. In “single” cue cases (D and M), stim1 and 2 differ in disparity-defined depth, but motion stays the same or vice versa. In combined cue conditions, disparity and motion can depict depth positions consistently (DM) or indicate opposite depths (D-M).

(B) Predictions for fusion (left) versus independence (right) mechanisms. In criterion 1, the fusion mechanism is compromised (lower performance) in the D-M condition, but the independence mechanism is unaffected because depth differences are detected independently. In criterion 2, the fusion mechanism is compromised by the “flat” cues in the D and M single cue conditions. In consequence, the ideal observer prediction (quadratic sum) underestimates DM empirical performance in the fusion case.