Two-State or Non-Two-State? An Excess Spectroscopy-based Approach to Differentiate the Existing Forms of Molecules in Liquids Mixtures

Abstract

Characterization/identification of the clusters/associates in liquids has long been a challenging topic. In this paper, we report a method to identify molecules with two different existing forms in a binary liquid solution. In this so-called two-state situation, the excess infrared spectra of a vibration mode of the respective molecule will show identical band shape if the other component is transparent in the region. More conveniently, the positions of the positive peak, negative peak, and zero-value will be seen to be fixed with varying compositions of the binary system. In the case of non-two-state mixtures, for example the mere solvation of solute by solvent, those positions will be variable. The conclusions are supported/demonstrated by computational simulation and experiments on two binary systems, D₂O−H₂O and C₆F₅I−cyclo-C₆H₁₂.

Liquids are much more complicated than gases and solids in the view point of theoretical treatment. They do not like gases which are typified by far molecular-separation and thus can be dealt with modified perfect gas law, nor do they like crystals which have definite structures and thus can be treated by the laws of solid-state physics. The biggest challenge in the study of liquids has been to describe their structures¹.

The earliest models take liquids as totally disordered structures. Later on, it was found that liquids are long range-disordered and short range-ordered². The presence of particular interactions such as hydrogen bonding³,⁴, halogen bonding⁵, and π–π stacking interactions⁶, will result in molecular association. It has been hypothesized that the associates could be dimer, trimer, tetramer, and multimers, either in linear, cyclic, or even branched forms⁷,⁸. If the associates are very stable and thus can be considered as discrete species, mass spectroscopy and methods to determine molecular weight such as freezing point depression can be of help. Unfortunately, most associates are not very stable, and can even be short-lived. To identify these not-very-stable associates, therefore, has been a long standing unsolved problem. In this paper, we report our effort to identify the associates using excess infrared spectroscopy.

Infrared spectra provide rich information of molecular structures. The absorption bands, however, are heavily overlapped for liquid samples. The concept of excess spectroscopy, proposed in our laboratory⁹,¹⁰, can improve the resolution to some extent. For example, by examining the O−H stretching band of tert-butanol–tetrachloride binary mixtures, we were able to identify four species in the mixtures, namely monomer, dimer, trimer, and multimers¹⁰. Other than this binary system, a number of binary systems including ionic liquids and molecular solvents have been investigated¹¹,¹²,¹³. One interesting phenomenon is that the positions of some excess peaks are independent of concentration. As exemplified in Fig. 1(a,b), the excess peaks over the ν(O−H) in C₂H₅OH−CD₃CN system (a) and ν(O−H) stretching in tert-butanol−CCl₄ system (b) show fixed positions¹⁰,¹³.

Figure 1. Excess infrared spectra.

(a) O–H stretching in C₂H₅OH−CD₃CN system¹³. (b) O–H stretching in tert-butanol–CCl₄ system¹⁰. (c) C ≡ N stretching in CD₃CN–CCl₄ system. Mole fractions of the binary mixtures have been indicated by the respective curves in the figure.

It should be stressed that not all the excess peaks behave like this. The positions can be concentration-dependent as shown in Fig. 1(c) for ν(C ≡ N) stretching in CD₃CN−CCl₄ system. Intuitively, the fixed position of an excess band should mean something, most likely a reflection of identical configuration of the concerned bond, plus the same or close solvent environment to the respective vibrational mode. In this paper, we will show that this is true under certain conditions, particularly when there are only two existing forms of the concerned molecules. By changing the concentration of the mixtures, the amount of the two forms will change. This is regarded as a two-state transformation.

The significance of the present work lies also on its correlation to the in-situ identification of molecular clusters in liquids. Up to date, there have been some experimental methods to investigate molecular clusters¹⁴. But they are almost all for gas phase identification. For liquid state samples, for example water, their clusters have been studied by spraying the samples into inert solvent such as liquid helium¹⁵,¹⁶. Molecular clusters identified by these methods cannot reflect the real situations in liquids. Recently, Ben-Amotz and co-workers proposed that solvent molecules in a solution can be classified as bulk and solvation-shell molecules¹⁷,¹⁸,¹⁹. They used a multivariate curve fitting method to extract the spectrum of the latter. In principle, the idea can be used to extract the spectra of molecular clusters, while the detailed information of those clusters, including their types and spectroscopic properties, is required to be known. As a matter of fact, we have to accept that unambiguous in-situ identification of molecular clusters in pure liquids and liquid mixtures is an unsolved problem. The method proposed in this work gives a solution to the case when there are two existing forms of the target molecule in a binary system. The two forms can be two types molecular clusters or one type cluster plus monomer of the concerned component.

Results and Discussion

Theory

We consider a binary system. For each of the two components, the absorbance at a selected wavenumber is described in the form of Beer-Lambert Law:

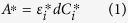where ε_i* and C_i* are the molar absorption coefficient and the molarity of the compound i in pure form, redspectively, d the light path. In the case of the binary mixtures, we assume the form of Beer-Lambert Law is still applicable:

where C = C₁+C₂. Generally speaking, absorption coefficient ε of the mixture is not a constant, but a function of wavelength and concentrations.

We define the absorption coefficient of an ideal mixture as:

where x₁ and x₂ are mole fractions of the two components. Then, the excess infrared spectrum, in the form of excess absorption coefficient, is defined as follows:

Now we purposely identify an absorption band of component 2 (solute, M), which is not overlapped with absorption bands from the other component (solvent, S). This means that the respective wavenumber range is transparent to the solvent. We assume that there are two existing forms of the solute, for example with and without forming complex with solvent (M₁ and M₂), over the entire or part of the concentration range. Their molar absorptivities are denoted as ε₂₁ and ε₂₂, which are independent on concentrations. The amounts of the two forms of the solute, however, are variable. The fraction of form 1 is denoted as δ over the two forms of the solute. In the absence of solvent, the fraction is δ₀. With these parameters, Equation (3) turns to be

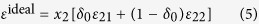Molar absorptivity of the real binary mixture is,

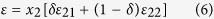Then, based on Equation (4), excess molar absorptivity of a real binary mixture is,

It is thus clear that the term defines the shape of an excess spectrum band, which is independent of the apparent concentration of the binary system. Only when the molar absorptivities of the two forms of the solute equal to each other, the excess function can be zero. Thus we conclude that the peak positions and zero-intensity frequency of the excess spectroscopic bands are all fixed in a series of binary mixtures, if there are only two existing forms of the solute and the solvent is transparent over the examined wavenumber range.

Digital simulation

With the above theoretical analysis, we have performed some digital simulation of excess infrared spectra to show the ideal appearance of the excess infrared spectra. Here, a single absorption band is expressed by the Lorentzian function as follows,

where w represents the full width at half-height, ν₀ the center position of band, and ε₀, the molar absorptivity when ν = ν₀. When there are two forms of the solute molecules in the binary system, the spectral function is expressed as follows,

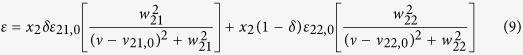The two peak positions are arbitrarily set at ν_21,0 = 3275 cm⁻¹ (State 1) and ν_22,0 = 3305 cm⁻¹ (State 2). By assigning the following parameters: ε_21,0 = 1, ε_22,0 = 0.9, w₂₁ = 80, w₂₂ = 70, the absorption bands representing the two states of the molecules can be derived and the results are shown in the inset of Fig. 2(a). Assuming pure M only exists in the form of State 1, and when the mole fraction of M decreases, the fraction of State 1 in M also decreases in the M−S binary system. Thus giving a series of apparent concentration x₂ =1, 0.8, 0.6, 0.4, 0.2, and 0, we assume δ = 1, 0.7, 0.45, 0.25, 0.1 and 0. IR spectra and excess infrared spectra are simulated and the results are shown in Fig. 2. As can be seen in Fig. 2(a), the absorption peak looks like singular and it shifts gradually to higher wavenumber with increasing solvent concentration. Apparently, the blue shift would have been caused by solvation effect.

Figure 2.

Simulated infrared spectra (a,c) and the respective excess spectra (b,d) for the two-state transformation system. The dashed and dash-dot dotted lines in (a,c) depict spectra of pure M and S. The inserts are: the absorption bands representing the two existing forms of the molecules in their pure states (a,c), overlapping presentation of the excess curves (b,d).

The excess infrared spectra shown in Fig. 2(b) provide correct insights of the system. Apart from showing a positive peak at the higher wavenumber side and a negative peak at the lower wavenumber side in each curve, which is the same with solvation effect, the spectra give fixed positions of positive and negative peaks at 3314 and 3264 cm⁻¹, respectively. Meanwhile, the zero-value points of the four excess spectra appear at identical position. Different values of the parameters generate excess infrared spectra with different shapes. When there is significant difference between the two w values, namely one broad peak overlaps with a very narrow peak, two zero-value points can be seen. Shown in Fig. 2(c,d) is one such example where ε_21,0 = 1, ε_22,0 = 1.4, w₂₁ = 200, w₂₂ = 90. Even in this case, the positive and negative peak positions and the zero-value positions are all fixed.

We also examined the solvation effect, where an infrared absorption band of component 2 shifts gradually. To do the simulation, we first constructed an absorption peak of component 2 centered at 3275 cm⁻¹ with ε_2,0 = 1 and half peak width w₂ = 80. Then the mole fraction of the component 2 decreases by 0.2 each step, and at the same time the absorption peak shifts to higher wavenumber by 10 cm⁻¹. The Lorentzian peak is described as follows

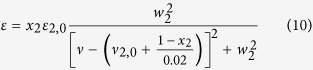The simulated infrared spectra as shown in Fig. 3(a) are quite similar to those in Fig. 2(a). The simulated excess infrared spectra, however, show completely different results. The positions of both positive and negative peaks, as well as the position of the zero-value point, are not fixed.

Figure 3.

Simulated infrared spectra (a) and excess infrared spectra (b) in the presence of solvation effect. The dashed and dash-dot dotted lines in (a) depict spectra of pure M and S, respectively. The insert is the overlapping presentation of the excess curves.

If two distinct states and solvent effects are combined, or there are more than two distinct states of the solute, the Equation (7) will not hold anymore. More or less, the positions of the positive and negative peaks will subject to changes. Nevertheless, our simulation indicates that, depending on the extent of hydration or the relative separation of the multi-state peaks, positions of part or all of the peaks in the excess spectra can be relatively fixed (see Supplementary Information). We, therefore, conclude that if the position of an excess peak is relatively fixed, most likely it represents a distinct species.

D₂O−H₂O system

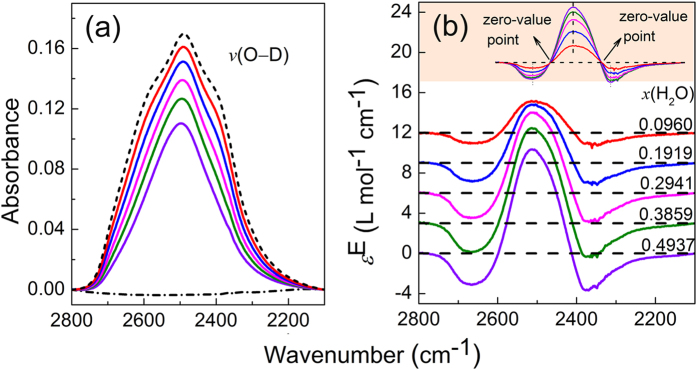
The hydrogen/deuterium atoms in a water molecule are not bonded to one molecule forever, but rather they can exchange with the hydrogen/deuterium in the neighboring molecules. Consequently, the H and D atoms in D₂O−H₂O mixture will switch one another to form the third species, HDO²⁰,²¹. In D₂O−H₂O binary system, there are two kinds of O−D, those in HDO and in D₂O. This is the case of two-state transformation upon changing concentration.

The partial ATR-FTIR and excess spectra of D₂O−H₂O system in the O−D stretching region are shown in Fig. 4. Normal water has no absorptions in the wavenumber region. The absorption band in Fig. 4(a) is assigned to ν(O−D) according to literature²⁰. In Fig. 4(b), the excess spectra show two fixed-position negative peaks, one fixed positive peak, and two fixed zero-value points, which are the same as the simulation result shown in Fig. 2(d). This demonstrates that, in the binary system with two-state transformation, both the excess peaks and zero-value points are fixed.

Figure 4.

Infrared spectra (a) and the respective excess infrared spectra (b) of D₂O–H₂O system in the range of the O–D stretching vibration. The dashed and dash-dot dotted lines in (a) depict spectra of pure D₂O and H₂O, respectively.

C₆F₅I− cyclo-C₆H₁₂ system

The C₆F₅I–cyclo-C₆H₁₂ system was also studied by ATR-FTIR technique. The IR and excess infrared spectra of the C₆F₅I–cyclo-C₆H₁₂ system in the C–I stretching region are shown in Fig. 5. The band at 805 cm⁻¹ is attributed to the C−I stretching vibration²². In Fig. 5(a), from top to bottom, the peak position is blue-shifted. In Fig. 5(b), the excess spectra show fixed positions of positive peak, negative peak, and zero-value points, which are in consistent with the simulation results shown in Fig. 2(b). This strongly suggests that C₆F₅I–cyclo-C₆H₁₂ system exists in two distinct states upon dilution with cyclo-C₆H₁₂. For C₆F₅I, cyclo-C₆H₁₂ is an inert solvent. So the two states may be attributed to the absorptions of monomer and self-aggregated C₆F₅I¹². Most likely, the self-aggregated C₆F₅I is the dimer of the molecule. Quantum chemical calculations were performed to find the optimized structure of the C₆F₅I dimer, which is shown in the inset of Fig. 5(a). As can be seen, the two molecules form a displaced π−π stacking interaction pair. The distance of the two planes is 0.303 nm. The interaction energy is −100.25 kJ/mol, suggesting the dimer is quite stable. Furthermore, the calculated frequencies of v(C−I) indicate that there is a redshift upon formation of dimer. Thus the negative peak at lower wavenumber is assigned to dimer and the positive one to monomer.

Figure 5.

Infrared spectra (a) and excess infrared spectra (b) of the C₆F₅I–cyclo-C₆H₁₂ system at different mole fraction of C₆F₅I in the wavenumber range of the C–I stretching vibration. The dashed and dash-dot dotted lines in (a) depict spectra of pure C₆F₅I and cyclo-C₆H₁₂, respectively.

Conclusions

In this paper, we developed a method to differentiate two-state and non-two-state of molecular exiting forms in binary liquid mixtures, based on the excess spectroscopic technique. If a molecule exists in two forms over a range of concentration in a binary mixture, the excess band of a vibration mode of the molecule will show fixed peak positions and zero-intensity frequencies in the concentration range if the other component has no absorption in the region. Otherwise, these positions should be concentration-dependent. These features are demonstrated with numerical simulation and experiments. In D₂O−H₂O system, there are two O−D stretching forms. They are readily assigned to that from D₂O and DOH. In C₆F₅I–cyclo-C₆H₁₂ system, the excess infrared spectra in the C−I stretching region suggest that there are two forms of C₆F₅I during the mixing process. They are most likely self-aggregated and non-aggregated C₆F₅I. The aggregation is believed to be in the form of displaced π−π stacking. For more complicated situations such as the coexistence of three or more forms of the concerned component, the feature/shape of the excess spectra will be concentration-dependent. But if the position of a positive peak or negative peak in a series of excess spectra is relatively fixed, most likely it indicates a distinct species.

Methods

Chemicals

D₂O (>99%) was purchased from Armar Chemicals. C₆F₅I (>98%) was purchased from J&K Scientific. Cyclo-C₆H₁₂ (>99%) was from Beijing Chemical Plant (Beijing, China). The samples were used without further purification.

Sample preparation

A series of D₂O−H₂O and C₆F₅I–cyclo-C₆H₁₂ binary mixtures were prepared by weighing. The mole fractions of H₂O in D₂O−H₂O mixtures are 1, 0.4937, 0.3859, 0.2941, 0.1919, 0.0960, and 0. The mole fractions of C₆F₅I in C₆F₅I–cyclo-C₆H₁₂ mixtures are 1, 0.8815, 0.7928, 0.7073, 0.5996, 0.5027, 0.3888, 0.2918, 0.2044, 0.1050, and 0.

FTIR spectroscopy

FTIR spectra over the range from 4000 to 650 cm⁻¹ were collected at room temperature (~25 °C) using a Nicolet 5700 FTIR spectrometer, equipped with an MCT detector. Two ATR cells made of trapezoidal ZnSe/Ge crystals were used in the experiments. A ZnSe crystal with an incident angle of 45° and 12 reflections was used to examine the stretching bands of O−D in D₂O−H₂O system. A Ge crystal with an angle of 60° and 7 reflections was used to examine the strong stretching bands of C−I in C₆F₅I–cyclo-C₆H₁₂ system. Spectra were recorded with a resolution of 2 cm⁻¹, a zero filling factor of 2, and 32 parallel scans. The refractive indexes of solutions were measured with a refractometer at 25 °C. The formulas suggested by Hansen²³, were used to do the ATR corrections.

Excess infrared spectroscopy

The theory of excess infrared spectroscopy has been described in detail elsewhere⁹,¹⁰. Briefly, an excess infrared spectrum is defined as the difference between the spectrum of a real solution and that of the respective ideal solution under identical conditions. The working equation in calculating the excess infrared spectrum is as follows:

where A is the absorbance of the mixture, d is the light path length, C₁ and C₂ are molarities of the two components, x₁ and x₂ are mole fractions of components 1 and 2, and ε₁^* and ε₂^* are molar absorption coefficients of the two components in their pure states, respectively. The calculation of the excess infrared spectra was programmed using Matlab 7.0 (Math Works Inc., Natick, MA).

Quantum chemical calculations

Quantum chemical calculations were performed by employing second-order many-body perturbation theory (MP2) at mixed basis sets with the Gaussian 09 program²⁴. The molecular geometry were fully optimized with the LANL2DZ²⁵, basis set for iodine atom and the aug-cc-pVDZ²⁶, basis set for hydrogen, carbon, and fluorine atoms. All the optimized geometries were recognized as local minima with no imaginary frequency.

Additional Information

How to cite this article: Zhou, Y. et al. Two-State or Non-Two-State? An Excess Spectroscopy-based Approach to Differentiate the Existing Forms of Molecules in Liquids Mixtures. Sci. Rep. 5, 16379; doi: 10.1038/srep16379 (2015).