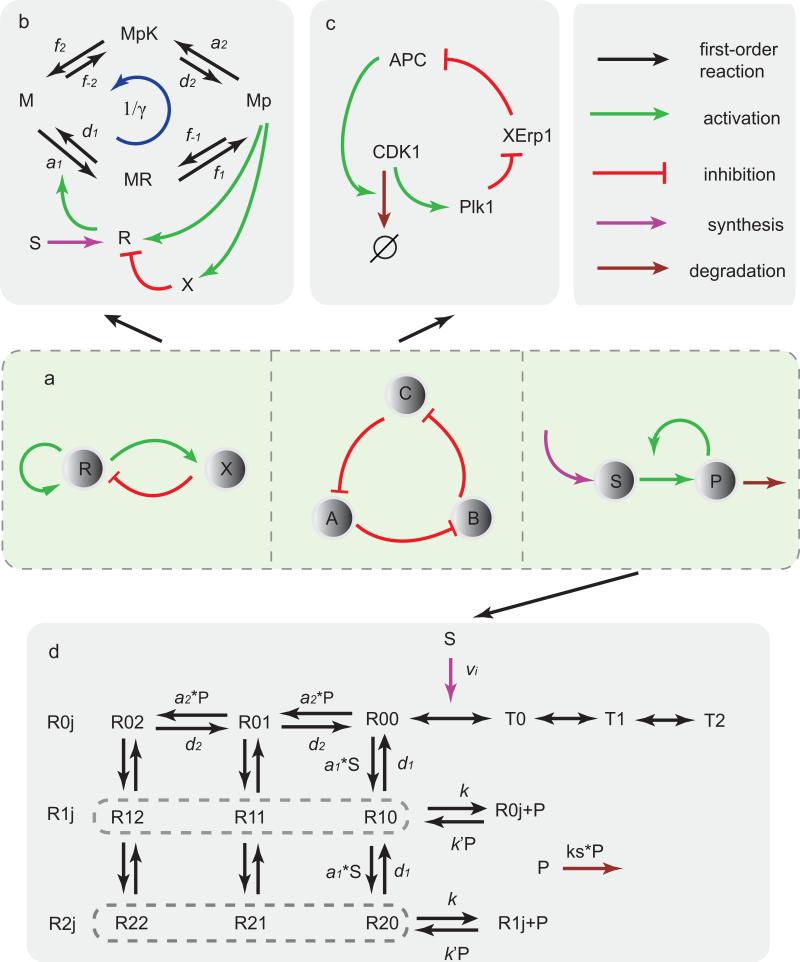
Figure 1.

Different network motifs and the corresponding biochemical oscillatory systems. (a) Illustrations of three network motifs for oscillation: activator-inhibitor, repressilator, and substrate-depletion. Lines with different colors stand for different reactions. (b) The activator-inhibitor model with a phosphorylation-dephosphorylation (PdP) cycle. R and K catalyse two opposing reactions M ↔ M_p (phosphorylation and dephosphorylation) through different intermediate complexes MR and M_pK. M_p activates both R (activator) and X (inhibitor). X inhibits R by enhancing its degradation. Parameter γ = d₁f_–1d₂f_–2/(a₁f₁a₂f₂) is introduced to characterize the reversibility of the system. S is the basic synthesis rate. (c) The “repressilator” model of cell cycle in eukaryotic cells. In the simplified network, CDK1 activates Plk1, Plk1 activates APC by suppressing the inhibitor of APC, XErp1, and APC degrades CDK1, forming the mutually activing/inhibiting loop. (d) The glycolysis network. The allosteric enzyme's protomer has two states, R (binding with P) and T (unbinding with P), and only R has the catalysis activity. Each R_i,j, with i = 1,2, ···, n_i and j = 1,2, ···, n_j represent the number of P and S bound to R, here we used n_i = n_j = 2. Each R_i,j can undergo reactions of R_i,j + S ↔ R_i,j+1 ↔ R_i,j + P. Detailed descriptions and rate values are given in SI.