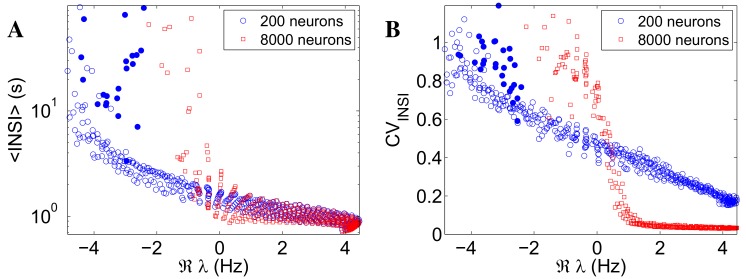
Fig 3. Stability analysis of the linearized dynamics captures most of the variability in the inter-network-spike interval (INSI) statistics.

〈INSI〉 (panel A) and CV_INSI (panel B) vs the real part ℜλ of the dominant eigenvalue of the Jacobian of the linearized dynamics, for two networks that are pointwise identical in the excitation-inhibition plane, except for their size (circles: 200 neurons, as in Fig 2; squares: 8000 neurons). The data points almost collapse on 1-D curves when plotted as functions of ℜλ, leading effectively to a “quasi one-dimensional” representation of the INSI statistics in the (w_exc, w_inh)-plane. The region in which the INSIs are neither regular (CV_INSI ∼ 0) nor completely random (CV_INSI ≃ 1), as typically observed in experimental data, shrinks for larger networks. The filled circles mark a null imaginary part ℑλ.