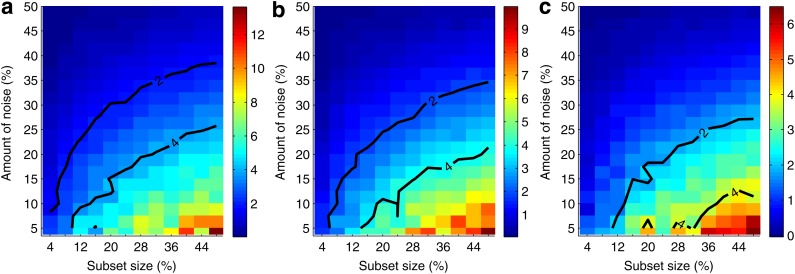
FIG. 7.

Information gain over background as a function of data size and amount of noise. Given a set of 5,000 samples and a subset size X, we randomly choose 10 subsets with size X. Then for each subset, we randomly seed noise up to a specified level and compute MI for all the pairs. We then repeat random noise assignment 100 times and do that for each subset. Finally we take an average for every pair. We also average MI for all noninformative pairs (other than 〈X₁₇, X₁₉〉, 〈X₁₂, X₁₉〉, and 〈X₁₁, X₁₉〉) into one value we call background MI. Three plots of the figure show heat maps for the three informative pairs, (a) 〈X₁₇, X₁₉〉, (b) 〈X₁₂, X₁₉〉, and (c) 〈X₁₁, X₁₉〉. Each point of the heat map corresponds to a difference between the average MI of the pair and the background MI for a given subset size and noise level. The difference is scaled by the size of the standard deviation of the MI of the pair, so the color bar corresponds to the number of standard deviations the average MI of the pair is from the average background MI. Two contours are shown for the difference equal to two and four standard deviations.