Harnessing Genetic Variation in Leaf Angle to Increase Productivity of Sorghum bicolor

Abstract

The efficiency with which a plant intercepts solar radiation is determined primarily by its architecture. Understanding the genetic regulation of plant architecture and how changes in architecture affect performance can be used to improve plant productivity. Leaf inclination angle, the angle at which a leaf emerges with respect to the stem, is a feature of plant architecture that influences how a plant canopy intercepts solar radiation. Here we identify extensive genetic variation for leaf inclination angle in the crop plant Sorghum bicolor, a C4 grass species used for the production of grain, forage, and bioenergy. Multiple genetic loci that regulate leaf inclination angle were identified in recombinant inbred line populations of grain and bioenergy sorghum. Alleles of sorghum dwarf-3, a gene encoding a P-glycoprotein involved in polar auxin transport, are shown to change leaf inclination angle by up to 34° (0.59 rad). The impact of heritable variation in leaf inclination angle on light interception in sorghum canopies was assessed using functional-structural plant models and field experiments. Smaller leaf inclination angles caused solar radiation to penetrate deeper into the canopy, and the resulting redistribution of light is predicted to increase the biomass yield potential of bioenergy sorghum by at least 3%. These results show that sorghum leaf angle is a heritable trait regulated by multiple loci and that genetic variation in leaf angle can be used to modify plant architecture to improve sorghum crop performance.

SUSTAINABLY increasing the productivity of crops on land currently used for agriculture without depleting natural resources is a global priority (Foley et al. 2011; Drewry et al. 2014). Improving the efficiency with which plants intercept solar radiation is one means to sustainably improve crop productivity. Leaf angle, or leaf erectness, is a plant canopy parameter that has drawn considerable attention because of the predicted improvement in photosynthetic efficiency and reduction in plant stress afforded by the redistribution of solar radiation from upper to lower levels of canopies (Tollenaar and Wu 1999; Duvick 2005; Murchie et al. 2009; Zhu et al. 2010; Murchie and Reynolds 2012; Drewry et al. 2014; Mansfield and Mumm 2014). Performance improvements predicted by theoretical models are corroborated by positive correlations between small leaf angles and cereal crop yields; post–green revolution rice cultivars have smaller leaf inclination angles and higher yields relative to their pre–green revolution predecessors (Yoshida 1972; Sinclair and Sheehy 1999; Sakamoto et al. 2006), and modern maize is also characterized by small inclination angles as a consequence of selection for increased grain yield in breeding programs (Duvick 2005; Lee and Tollenaar 2007; Hammer et al. 2009; Tian et al. 2011; Mansfield and Mumm 2014).

Despite the association of leaf angle with increased productivity, its genetic basis remains to be fully characterized for many of the major grasses. In maize, ligueless1 and ligueless2 have been identified as major regulators of leaf angle that can improve plant productivity (Pendleton et al. 1968; Lambert and Johnson 1978; Moreno et al. 1997; Walsh et al. 1998). More than 40 additional quantitative trait loci (QTL) have been identified in the maize nested association mapping (NAM) and recombinant inbred lines (RIL) populations (McMullen et al. 2009; Tian et al. 2011; Li et al. 2015). In rice, osdwarf4-1 and leaf inclination2 have been identified and shown to play roles in plant hormone responses that result in changes in leaf angle (Sakamoto et al. 2006; Zhao et al. 2010). Progress in identifying leaf angle QTL has been made in sorghum, the fifth most widely produced grain and forage crop, but a gene that regulates leaf angle has yet to be identified as has been done in maize and rice (Hart et al. 2001; Gill et al. 2014; Perez et al. 2014; Xin et al. 2015).

The physiological basis for the impact of leaf inclination angles on yield may be explained by altered vertical distribution of solar radiation in the canopy. Leaf positioning, a factor influenced by leaf inclination angle, can maximize carbon gain by optimizing interception of photosynthetically active radiation (PAR) for canopy photosynthesis and by mitigating heat stress induced by excess infrared radiation (IR) (Zhu et al. 2008, 2010; van Zanten et al. 2010; Song et al. 2013). In addition to mitigating the occurrence of excess radiation at the top of the canopy (Nobel 2005; Long et al. 2006; Zhu et al. 2010; Mullet et al. 2014), canopy architectures that have small upper leaf angles redistribute PAR more uniformly throughout the canopy, thereby reducing shade-induced senescence of lower leaves (Hurng et al. 1986; Sinclair and Sheehy 1999; van Zanten et al. 2010; Song et al. 2013). The resulting increase in green leaf area allows for greater accumulation of nitrogen, a possible rate-limiting factor during grain filling in modern high-yield cultivars (Drouet and Bonhomme 1999; Sinclair and Sheehy 1999; Hammer et al. 2009). More optimal vertical redistribution of solar radiation throughout the canopy also allows for denser planting of grain crops, an important factor contributing to increased grain yield per hectare (Sinclair and Sheehy 1999; Duvick 2005; Tian et al. 2011; Mansfield and Mumm 2014). For example, small leaf angles of the rice osdwarf-4 mutant and the maize liguleless2 mutant enabled higher-density planting that increased biomass yield of the respective crops (Lambert and Johnson 1978; Sakamoto et al. 2006).

Given successes in other grass crops, there is strong motivation for identifying the genetic basis of leaf angle and determining its physiological consequences in sorghum, particularly for bioenergy sorghum. High-biomass energy sorghum hybrids have long growing seasons and accumulate most of their biomass in tall (∼4 m) closed canopies (Rooney et al. 2007; Olson et al. 2012; Mullet et al. 2014). Over the long bioenergy growing season, small daily improvements in energy conversion efficiency conferred by more optimal leaf angles could translate into large seasonal increases in biomass accumulation. We examined the genetic basis of leaf inclination angle in sorghum using both grain and bioenergy sorghum RIL populations and identified multiple QTL contributing to the regulation of leaf angle. Moreover, we demonstrate that a leaf angle QTL present in grain sorghum germplasm is caused by sorghum dwarf-3 (a homolog of maize br2) and that the recessive allele of sorghum dwarf-3 decreases leaf inclination angle up to 34° (0.59 rad). Additionally, we use functional-structural plant modeling and field experiments to show that smaller leaf inclination angles cause solar radiation, including PAR, to penetrate deeper into energy sorghum canopies. The improvement in conversion efficiency afforded by the redistribution of PAR is predicted to increase the biomass yield of bioenergy sorghum over the growing season by at least 3%. Given these results, genetically optimizing leaf angle represents a promising way to sustainably increase sorghum productivity.

Materials and Methods

Genetic basis of leaf inclination angle

Two recombinant inbred line populations generated from biparental crosses of BTx623 × IS3620c (n = 398) and R07018 × R07020 (n = 96) were used to examine the genetic basis of leaf inclination angle in Sorghum bicolor (Burow et al. 2011; Bartek et al. 2012). Individuals from these populations were genotyped by sequencing using the restriction enzyme–based reduced representation technique Digital Genotyping (Morishige et al. 2013). Template DNA was prepared using the restriction enzyme NgoMIV for the BTx623 × IS3620c population and FseI for the R07018 × R07020 population. Libraries were sequenced with an Illumina HiSeq 2500. Reads were mapped to the sorghum reference sequence (Sbi1) with the Burrows-Wheeler Aligner (BWA v0.7.5.a) (Paterson et al. 2009; Li and Durbin 2010). Aligned reads were processed with Picard (v1.108), and variant calls (SNPs and indels) were generated using the GATK (v3.2-2) by following the naive pipeline of the RIG workflow (McKenna et al. 2010; Depristo et al. 2011; Van der Auwera et al. 2013; McCormick et al. 2015). Subsequent genetic maps were generated using R/qtl (Broman et al. 2003). The BTx623 × IS3620C genetic map contained 10,091 markers and was constructed as described in Truong et al. (2014) under a model of excess heterozygosity. Genotype data for R07018 × R07020 were quality controlled in a similar manner, and a genetic map containing 1968 markers was estimated as an F₅ using the BC_sF_t Tools in R/qtl. Genetic maps and genotype data are available in the Supporting Information, File S2.

Phenotyping leaf inclination angle

The two experimental crosses used to study the genetic basis of leaf inclination angle, BTx623 × IS3620c and R07018 × R07020, were planted and phenotyped in College Station, Texas, in a greenhouse and in experimental fields. Table 1 provides information on where, when, and the number of individuals from each population that were planted and phenotyped. Phenotypes used in heritability calculations and QTL mapping were the average of the biological replicates measured (Table 1). To phenotype leaf inclination angle, leaves were counted by starting from the youngest ligulated leaf to the older leaves further from the top the plant. That is, at the time of phenotyping, the youngest fully expanded leaf (below the whorl) was identified as leaf 1, and each subsequent leaf was numbered sequentially (e.g., leaf 3 was two leaves below leaf 1). Leaf inclination angle was measured with a protractor; the origin (pinpoint) was placed where the leaf midrib would meet the stem. The angle measured was between the stem and the adaxial midrib of the leaf (the axil).

Table 1. Experimental crosses and phenotyping metadata.

Cross generation	RILs (n)	Location (College Station, TX)	Planting		Phenotyping
			Date	Structure	Date(s)	Reps.
BTx623 × IS3620c  F6–8	88	Field	03/27/2013	One-row plot	06/20/2013, 06/26/2013, 06/30/2013	3
	336	Greenhouse	05/27/2014	Two per pot	07/04/2014–07/05/2014	2
	7	Field	04/08/2014	One-row plot	06/18/2014–06/19/2014	4
R07018 × R07020 F5	94	Greenhouse	07/30/2013	Three per pot	09/07/2013	3
	94	Field	04/08/2014	One-row plot	06/27/2014	3
	94	Field	04/08/2014	One-row plot	07/31/2014	3
	2	Field	04/08/2014	Four-row plots	07/22/2014–07/26/2014	10

This table contains the two biparental crosses used, the number (n) of RILs assayed, the location, time, and structure of planting, the number of biological replications phenotyped (i.e., number of plants), and the time at which measurements were acquired. Row plots in the field are planted mechanically and are 0.76 m apart and have a planting density of approximately 13.2 plants/m².

Stepwise multiple-QTL mapping and heritability estimates

Stepwise multiple-QTL analysis was performed on the genotype and phenotype data described earlier to identify the QTL and epistatic interactions between them that best describe the genetic basis of variation in leaf inclination angle phenotypes. Phenotype data were normalized by empirical normal quantile transformation (Peng et al. 2007). A single QTL analysis using the expectation-maximization (EM) algorithm initially identified primary additive QTL, and this was used to seed model selection for multiple-QTL analysis. We employed the method of Manichaikul et al. (2009) for model selection as implemented in R/qtl (Broman et al. 2003). This method considers the LOD score for a multiple-QTL model penalized by the complexity of the model, using penalty scores specific to each phenotype. We used computational resources on the Whole Systems Genomics Initiative (WSGI) cluster at Texas A&M University to calculate the penalties for main effects, heavy interactions, and light interactions; these penalties were calculated from 24,000 permutations of each phenotype from each population with genetic markers that were 2 cM apart (∼600 markers) to find a significance level of 5% in the context of a two-dimensional two-QTL genome scan; penalized LOD (pLOD) scores are listed in File S2.

We chose a parsimonious QTL model for each phenotype to report here (detailed statistics of each QTL model are provided in File S2). The models chosen are less prone to false-positive results in our approach to QTL model selection because we required additional QTL and interactions to increase the pLOD of the QTL model by at least its LOD penalties for main and light interactions, respectively. We did not choose an exhaustive QTL model, and less stringent QTL models for the phenotypes are possible.

In addition to variance explained by the QTL, we also estimated the variance explained by SNPs and indels across the genome for each phenotype using GCTA (Yang et al. 2011). The genetic variants that were used as input to genetic map construction (prior to the quality control involved in map construction) were quality controlled using PLINK v1.90b3u (Purcell et al. 2007), and heritability was estimated using a genomic relationship matrix (GRM) and restricted maximum likelihood (REML) as implemented in GCTA. This analysis estimates the proportion of observed phenotypic variance-covariance relationships among the lines that can be explained by the whole-genome relatedness of the lines estimated by markers, providing an estimate of narrow-sense heritability (Yang et al. 2013).

dw3 gene identification

The dwarf-3 (dw3) gene is well known for its effect on stalk height in S. bicolor. The common, nonfunctional dw3 allele contains an 882-bp tandem duplication in exon 5 that causes the loss of function; the null dw3 allele is genetically unstable and can revert to the functional Dw3 allele when the 882-bp duplication is removed by unequal crossing over (Multani et al. 2003). The reversion event is visually identifiable when it occurs in field plots of isogenic sorghum because the revertant is taller than its surrounding siblings. Seven dw3 revertants were identified in rows of recombinant inbred lines of BTx623 (dw3dw3) × IS3620c (Dw3Dw3) planted in College Station, Texas, fields in 2014 (Figure S1). The revertants and three of their nonrevertant siblings were genotyped by PCR to amplify a region of dw3; genotypes that contained one or two copies of the 882-bp DNA correspond to the functional and nonfunctional alleles, respectively. The primers used were designed by Farfan et al. (2012).

Calculation of the light extinction coefficient k

Light interception throughout crop canopies is often formalized as an extinction coefficient k (as derived in Beer-Lambert’s law) that relates the attenuation of light with properties of the material through which the light travels (Monteith and Moss 1977; Monsi and Saeki 2005; Nobel 2005; Long et al. 2006). Here we use the equation

$$I\left(x\right)=I_0{e}^{-kx}$$ (1)

Given data ${\left\{x_n,I\left(x_n\right)\right\}}_{n=1}^N$, where $I\left(x\right)$ is the intensity (power per unit area) of radiation from the sunlight at depth x down the canopy, we can estimate the light extinction coefficient k by fitting with the Levenberg-Marquardt algorithm for nonlinear least squares (Jones et al. 2001). A detailed explanation of the function and its adoption to describe the vertical distribution of sunlight in a crop canopy is provided in File S1. We use k as a descriptor to characterize and compare the distribution of light in simulated and field-grown sorghum canopies with differing leaf inclination angles.

Virtual sorghum canopies

We constructed functional-structural plant models of sorghum and collected depth and incident-light data ${\left\{x_n,I\left(x_n\right)\right\}}_{n=1}^N$ in simulated light environments and calculated values of theoretical k. The three-dimensional virtual sorghum plants were constructed using Lindenmeyer systems in L-py (Boudon et al. 2012). Lindenmeyer systems provide a set of production rules whereby plant structural models are produced by recursion through phytomers (Prusinkiewicz et al. 2012). The virtual canopies were then illuminated by the nested radiosity model as implemented in CARIBU (Chelle and Andrieu 1998; Chelle et al. 2004; Pradal et al. 2008) given light input that reflected solar conditions in College Station, Texas (data retrieved from the U.S. Naval Observatory, aa.usno.navy.mil). Details on methods of construction and the scripts used can be found in File S2.

Field experimental sorghum canopies

Two sorghum RILs, RIL 63 and RIL 73, were identified as lines with large phenotypic variation in leaf angle when phenotyping the R07018 × R07020 RIL population grown under greenhouse conditions (Bartek et al. 2012). To study the effect of leaf angle on light penetration at different depths in the plant canopy, two adjacent plots, one plot of RIL 63 and one plot of RIL 73, were planted in College Station, Texas, fields (W96°20", N30°37"); each plot had four rows with row spacing of 0.76 m² and was planted at a density of 13.2 plants/m². To estimate k values for each of the two plots, light penetration at multiple layers in the canopy was measured for seven collections using two lifts and two PAR meters (LP-80, Decagon Devices, Inc., Pullman, Washington) to simultaneously take readings at the same canopy height in the two canopies (File S1, Figure S2, and Table S1). All plot and plant measurements along with raw depth from the experimental field data, subsequent scaling employed, and their fits to equation (1) are available in File S2.

Estimating potential biomass gain

The calculation of biomass yield gain is based on the gain of solar conversion efficiency on a per-leaf basis of C4 plants. We used energy absorbed at each sequential leaf through the canopy (predicted by the CARIBU model) and estimated the conversion efficiency provided by Zhu et al. (2010). Conversion efficiency is modeled as a linear parameter in the Monteith equation for biomass (Zhu et al. 2010), and thus the biomass yield gain is the same amount as the efficiency gain. The calculations made are available in File S2 as a spreadsheet.

Data availability

Data and analyses, including genetic maps, genotypes, phenotypes, and analysis code are contained in File S2, hosted at https://github.com/mulletlab/leafangle_supplement.

Results

Genetic regulation of sorghum leaf angle

Given that leaf inclination angle is associated with productivity increases in other crop plants (Sinclair and Sheehy 1999; Duvick 2005; Tian et al. 2011; Mansfield and Mumm 2014), we sought to identify genetic loci that regulate leaf angle in sorghum. Identification of genetic loci that modulate leaf angle will enable both experimental analyses of the effect of leaf angle on radiation use efficiency (RUE) and nitrogen status and deployment of favorable alleles into breeding programs. Genetic analyses were carried out using two RIL populations derived from the following biparental crosses: (1) grain sorghum lines BTx623 and IS3620c and (2) late-flowering bioenergy sorghum lines R07018 and R07020.

Leaf angle is developmentally regulated and changes based on leaf age; leaves at the top of a plant typically have small leaf angles and minimal variation that could be attributed to genetics (see File S1). As such, the angles of the third and fourth (and fifth when not senesced) fully expanded ligulated leaves, counting from the uppermost fully expanded leaf at the top of the plant, were measured in the two RIL populations at varying stages of development as grown in the field and in greenhouses (Table 1). Model selection of multiple-QTL mapping analyses as described in Manichaikul et al. (2009) identified three loci in the grain population (BTx623 × IS3620c) and four loci in the bioenergy population (R07018 × R07020) that affected leaf inclination angle (P < 0.001; Table 2). In a given population, leaf number, and environment, the proportion of phenotypic variance explained by the multiple-QTL model was always greater than 15%. Given that the small population sizes used here for mapping can inflate QTL variance estimates via the Beavis effect (Beavis 1994, 1998; Xu 2003), we also estimated the proportion of phenotypic variance explained by genome-wide SNPs and indels, as described in Yang et al. (2011). Given the relatedness of individuals in the populations, the proportion of phenotypic variance explained by the SNPs and indels using a GRM and REML (as implemented in GCTA) approximates the narrow-sense heritability of the trait (Yang et al. 2013). Heritabilities of each leaf angle ranged from 9 to 62% depending on the population, location, and plant age (Table 2). Heritabilities in the BTx623 × IS3620c population were much larger owing to the large effect of the dw3 locus (discussed later); the dominant Dw3 allele is fixed in R07018 and R07020 and does not segregate in the bioenergy population (Figure S3).

Table 2. Trait heritability and QTL of leaf inclination angle.

Cross	Phenotyped	Leaf no.	Heritability ($\widehat{{\mathit{h}}^2}$)	QTL
				Chr.	LOD2 (Mbp)	Variance (%)
BTx623 × IS3620c	Fields; 90 DAP (n = 88)	3	0.62***	7	57.6–59.1a	37
		4	0.60***	1	55.6–60.4	12
				7	57.6–59.2a	38
	Greenhouse; 38 DAP (n = 336)	3	0.54***	7	58.3–58.8a	37
		4	0.50***	5	2.7–4.8	5
				7	58.3–58.8a	33
R07018 × R07020	Greenhouse; 39 DAP (n = 94)	3	0.39***	1	53.7–54.8b	24
		4	0.31***	1	13.6–61.3b	20
	Fields; 80 DAP (n = 94)	3	0.12**	7	55.2–58.3b	16
		4	0.23**	1	13.1–54.7b	19
		5	0.33***	1	13.1–15.2b	20
				1	53.4–54.7b	17
	Fields; 114 DAP (n = 94)	3	0.09*	3	5.6–61.1b	16
		4	0.12**	3	51.4–60.1	16
		5	0.14**	3	56.5–59.5	22

Estimates of trait heritability $\widehat{h^2}$ were approximated from estimations of variance explained by SNPs and indels across the genome for each phenotype (Yang et al. 2013). ***, **, and * denote P-values less than 0.0001, 0.05, and 0.1, respectively, for testing the null hypothesis that the trait is not heritable. All QTL models were chosen via model selection of multiple-QTL mapping analyses, as described in Manichaikul et al. (2009). All QTL were additive and have P-values < 0.001. The biparental cross, phenotype location (field or greenhouse), number of days after planting (DAP), individuals (n), and leaf number assayed in each experiment are given as metadata. The physical position [Sbi1, Paterson et al. (2009)] of largest LOD for each QTL and other statistics on the QTL models can be found in File S2.

^aLOD₂ intervals that contain the dw3 gene (chromosome 7: 58.55–58.56 Mbp).

^bLOD₂ intervals in which RILs 63 and 73 (the RILs used in field measurements of light extinction) are not genotypically identical.

dwarf-3 regulates leaf angle in sorghum

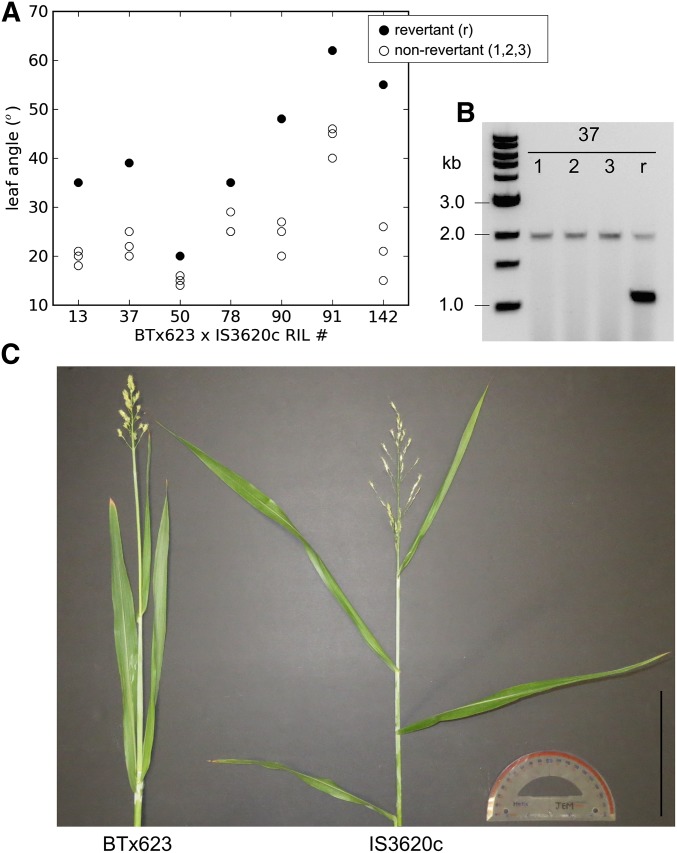
Comparisons between QTL mapping results for leaf inclination angle and plant height in the BTx623 × IS3620c RIL population showed identical marker association with both traits across an interval of chromosome 7 corresponding to the dwarf-3 (dw3) locus (data not shown). Previous reports also correlated alleles of dw3 with stem dwarfing and leaf inclination angle (Hart et al. 2001). Furthermore, dw3 is known to segregate in this mapping population, where BTx623 (dw3dw3) carries the nonfunctional dw3, an unstable allele that contains an 882-bp direct duplication that can revert to Dw3 by unequal crossing over (Multani et al. 2003), and IS3620c (Dw3Dw3) contains the functional Dw3 allele. The large phenotypic effect of the dominant Dw3 allele on height enables identification of tall revertants among dw3dw3 RILs. Therefore, we screened a field-grown subset of the BTx623 × IS3620c RIL population and identified revertant plants in seven different RIL plots by their increased heights. We found that the revertant plants with increased height also displayed large leaf inclination angles relative to nonrevertant plants (Figure 1 and Figure S1). Genotypes at the dw3 gene confirmed that the dominant Dw3 allele was present in the tall revertant plants. Dw3 revertant plants showed increases in leaf inclination angle of up to 34° (0.59 rad) relative to dw3 plants that were otherwise genetically identical individuals (Figure S1). Thus sorghum dw3 has a pleiotropic effect on both height and leaf angle.

Figure 1.

dw3 regulates leaf inclination angle. (A) Leaf 3 inclination angles of revertants (r) in filled black circles and nonrevertants (1, 2, 3) in empty white circles of seven RILs of BTx623 × IS3620c. (B) Genotypes of revertants and nonrevertants of RIL 37 at the dw3 locus using primers that flank the 882-bp tandem repeat that makes dw3 nonfunctional; unequal crossing over can lead to excision of one repeat copy and spontaneous reversion to the functional Dw3 allele (Multani et al. 2003; Farfan et al. 2012) (see Figure S1 for other RIL genotypes). (C) Parents, BTx623 and IS3620c, of the experimental cross in which revertants of dw3 were identified grown under greenhouse conditions. The protractor used to measure all leaf inclination angles here is also shown, and the scale bar is 6 inches.

Leaf angle affects vertical light distribution in sorghum canopies

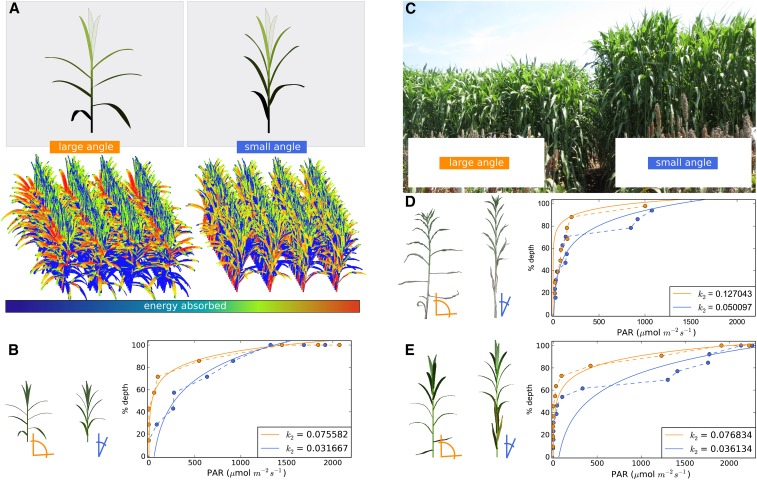
Once genetic loci regulating leaf inclination angle were identified, we sought to determine whether leaf inclination angle affects the distribution of solar radiation in the sorghum canopy and confers a functional difference in performance. To characterize and compare light interception by sorghum canopies with different leaf angles, the light extinction coefficients k of sorghum canopies were determined by modeling and using data from field measurements [equation (1)]. Given the same amount of available PAR, decreases in k translate to less PAR intercepted by upper layers of the canopy and more PAR available for interception at lower levels of the canopy (i.e., closer to the ground) (Monsi and Saeki 2005). We first compared the light extinction coefficient k of two simulated vegetative-phase grain sorghum canopies that intercepted all available light (Chelle et al. 2004; Pradal et al. 2008; Boudon et al. 2012). Plants in the simulated plots varying only in the leaf inclination angles of their fully expanded leaves were modeled under solar radiation conditions approximating a cloudless day in College Station, Texas, on July 13, 2013 (retrieved from U.S. Naval Observatory, aa.usno.navy.mil) (Figure 2A). The canopies with larger leaf inclination angles had a k that was two times larger than canopies with smaller leaf inclination angles, indicating that light was distributed more uniformly and deeper into the canopies of plants with small leaf inclination angles (Figure 2B).

Figure 2.

Leaf inclination angle affects light distribution in sorghum canopies. (A) Virtual sorghum plants and sorghum plots that vary in their leaf inclination angles (orange represents a larger leaf inclination angle relative to blue). (B) Light extinction curves for virtual plots from panel A simulated under solar conditions representing 13:00 on July 13, 2013, in College Station, Texas (W96°20", N30°37"). (C) Field plots of RIL 63 and RIL 73 from which light measurements were taken. (D) Light extinction curves for field plots from panel C assayed around 15:30 on July 22, 2014, in College Station, Texas. (E) Light extinction curves for virtual plots representing RIL 63 and RIL 73 simulated under solar conditions representing 15:30 on July 22, 2014, in College Station, Texas. In both simulation and field studies, plots with smaller leaf inclination angles fit a smaller light extinction coefficient k₂ relative to plots with larger leaf inclination angles (panels B, D, and E). k₂ values are derived from fits to equation (2) (see Materials and Methods).

To determine the extent that leaf inclination angle alters light distribution in canopies under field conditions, we identified two RILs from a biparental cross of bioenergy sorghum lines (R07018 × R07020), RIL 63 and RIL 73, that were phenotypically similar in all leaf traits measured except for leaf inclination angle (Figure S4). RIL 63 had a smaller leaf inclination angle at all phytomers compared to RIL 73 (Figure S4). Notably, RILs 63 and 73 from the R07018 × R07020 population had genotypic differences in three of the four QTL intervals affecting leaf angle identified by multiple-QTL mapping (indicated by b in Table 2); these genetic differences may underlie the large phenotypic differences in leaf inclination angle observed in these RILs. The two RILs were phenotypically similar with respect to stand density, leaf morphology, phytomer stem diameter and spacing, and biomass per unit height (Figure S4). Notably, RILs 63 and 73 varied with respect to the number of phytomers, leading to a difference in height and total biomass. Because of this height difference, measurements of k were scaled to percentage of canopy depth rather than absolute depth, although relative ordering of k values remains the same whether depth is scaled or not (Table S1). Four row plots of RILs 63 and 73 were planted in the field at College Station, Texas, in 2014 and analyzed after canopy closure in July. PAR was measured throughout the canopy seven times over the course of 4 days using two PAR meters mounted on a platform that could be moved to varying heights in the canopies (Figure S2 and Table S1). Six of the data sets showed that the plots containing plants with smaller leaf inclination angles distributed PAR to greater depths in the canopy, with two of the seven showing that the k of the large leaf inclination angle plots is more than twice as large as the k of the small leaf inclination angle plot (Figure 2D and Table S1).

While RILs 63 and 73 were phenotypically similar for most measured traits and genotypically different at most detectable leaf angle QTL (Table 2 and Figure S4), the possibility remained that their differences in light canopy penetration arose from factors not captured by the experiment, such as additional QTL regulating plant architecture. To investigate this possibility, simulated plants were parameterized using the measured phenotypes of RILs 63 and 73, including differences in phytomer number (and, consequently, height); traits not measured, such as leaf curvature, were kept constant, and the simulated plants were illuminated using field conditions. The light distribution plots generated by simulations were qualitatively similar to the field results (Figure 2, E and D). The possibility that differences in plant height and not leaf inclination angle were responsible for the smaller k of the small-angle plant was ruled out by removing phytomers so that the plant with small leaf angles, simulated RIL 63, was the same height as the plant with large leaf angles, simulated RIL 73; large leaf angles still caused k to be larger than small leaf angles (Figure S5). Fitting of the light extinction function [equation (1)] to the data revealed that the extinction model may not fully capture changes that occur in lower portions of the canopy (Figure 2, D and E). This suggests that the light extinction model’s assumption of a homogeneous canopy is an oversimplification (Song et al. 2013) and that factors such as leaf orientation and leaf senescence may need to be considered in future adjustments to the model.

We next determined whether the redistribution of incident PAR would be predicted to have a functional impact on biomass accumulation. Using estimates of conversion efficiency obtained from Zhu et al. (2010), we found that the redistribution of incident PAR in the simulated canopy with small leaf angles would cause an increase in overall conversion efficiency relative to the large leaf angle canopy. From this, we extrapolated a conservative estimate of biomass accumulation during a bioenergy sorghum growing season without water or nutrient limitations. For the virtual sorghum and lighting in Figure 2A, the conversion efficiency of the canopy with smaller leaf angles is predicted to be 1.0436 of the conversion efficiency of the canopy with large leaf angles. If we further assume that (1) the 4% gain in conversion efficiency is realized for 4 hr (midday) per 14-hr day and (2) the effect calculated is applicable to the duration of vegetative closed-canopy growth, then given a bioenergy sorghum growing season where 140 days are in the vegetative closed canopy of its 200-day growing season (Olson et al. 2012), we predict an overall increase of 3% conversion efficiency over the entire growing season. Thus, under these conditions, the canopy with smaller leaf angles has the potential to accumulate 3% more biomass than the canopy with large leaf angles. Since these performance differences are predicted from morphologically reasonable canopy parameters, leaf angle represents a realistic target to improve biomass yields without increasing input.

Discussion

This study has shown that leaf inclination angles are genetically regulated in S. bicolor and that leaf angle alters the vertical distribution of solar radiation in closed canopies under field conditions. The improved distribution of solar radiation is predicted to improve photosynthetic conversion efficiency of the canopy, resulting in a 3% gain in biomass yield for bioenergy sorghum. We found that the phenotypic difference in leaf angle between RIL 63 and RIL 73 corresponded with genotypic differences at most leaf angle QTL identified in the population from which they originated and that RIL 63 (with smaller leaf inclination angles) had a smaller light extinction coefficient k than RIL 73. Interestingly, RIL 63 also had more green leaf area and greater biomass than RIL 73. Additionally, while RIL 63 was taller, the length of each phytomer and biomass per unit height were similar (Figure S4), indicating that RIL 63 had an increased rate of phytomer production. This increase in phytomers and, in turn, biomass is consistent with the possibility that the small leaf angles of RIL 63 improved light interception and canopy conversion efficiency relative to RIL 73. Leaf appearance rate, or phyllochron, varies among sorghum genotypes during development and in response to the environment (Clerget et al. 2008; van Oosterom et al. 2011). In maize, field radiation intensity was negatively correlated with phyllochron (Birch et al. 1998). Determining whether the increased phyllochron in the small leaf angle genotype is a consequence of (1) differential genetic regulation of phyllochron, (2) lower radiation interception by upper leaves, and/or (3) increased photosynthetic conversion efficiency of the canopy will be investigated in future experiments. Additionally, prior work in maize and rice predict that the small leaf angles of RIL 63 will enable higher biomass accumulation at higher planting densities relative to RIL 73, so the effects of planting density also should be investigated (Lambert and Johnson 1978; Sakamoto et al. 2006).

Identification of dwarf-3, which encodes a P-glycoprotein that modulates polar auxin transport, as a regulator of leaf inclination angle by up to 34° (0.59 rad) in sorghum was shown by analysis of naturally occurring revertants. As with height, the action of the null dw3 allele on leaf angle is likely a consequence of reduced polar auxin transport from the shoot apical meristem (Multani et al. 2003; Knoller et al. 2010). Auxin was shown to regulate the establishment and propagation of the preligule band in maize plants with null alleles of liguleless1, liguleless2, and liguleless narrow (Moon et al. 2013), and P-glycoprotein (PGP) genes interact with PIN genes to influence local auxin distribution (Blakeslee et al. 2007; Mravec et al. 2008). Furthermore, rice LAZY1, a polar auxin transport repressor, regulates rice tiller angle via shoot gravitropism (Li et al. 2007; Dong et al. 2013), and maize ZmCLA4, an ortholog of rice LAZY1, increases shoot gravitropism and leaf angle at elevated expression levels (Zhang et al. 2014). Additional work will be necessary to determine the mechanism by which dw3 alleles regulate leaf angle. dw3 also regulates sorghum height, and the pleiotropic effects of dw3 explain observations from the sorghum literature, including a positive correlation between height and leaf angle in a sorghum grain association panel and increased leaf angle in some dw3 NILs (George-Jaeggli et al. 2013; Perez et al. 2014).

While dw3 had the largest effect on leaf angle of the loci reported here, the utility of dw3 for modulating leaf angle to improve sorghum productivity may be limited by its pleiotropic effects on height. Previous work has shown that the reduction in shoot biomass caused by dw3 reduces RUE and grain yield, which would likely offset any benefit afforded by small leaf angle for grain and bioenergy applications (George-Jaeggli et al. 2011, 2013). If the reduced productivity of grain sorghum with recessive dw3 is due to a reduction in stem reserves, as proposed by George-Jaeggli et al. (2011), any conversion efficiency benefits conferred by leaf angle would be constrained by the sink limitation caused by reduced stem size. The efficiency benefits of small leaf angles caused by the null dw3 allele may not be observed until recessive dw3 is put into a genetic background that is not sink limited. For bioenergy applications, it is likely that the reduction in height and biomass caused by recessive dw3 outweighs any productivity gains afforded by leaf angle, and other means of reducing leaf angle will be necessary. Fortunately, the genetic architecture underlying RIL 63 is promising because small leaf angles were associated with increased height and biomass.

In nature, large leaf angles may have been under positive selection because shading nearby plants would reduce competitors’ ability to compete for light and nutrients (Schmitt et al. 2003; Drewry et al. 2014). In monoculture grain cropping systems, small leaf angle has been under positive selection because this trait enables higher planting density and higher grain yield, presumably due to the benefits of improved RUE and increased nitrogen content of canopies (Drewry et al. 2014; Warnasooriya and Brutnell 2014). The design of C4 energy grass crops is at an early phase of development and could benefit from improved RUE afforded by small leaf angles (Mullet et al. 2014). Energy sorghum and grain sorghum canopies close 60–75 days after seedling emergence, approximately when grain sorghum reaches anthesis. In contrast, energy sorghum remains vegetative following canopy closure for an additional 140 days, and plants retain a whorl of developing leaves at the top of the canopy that have very small angles (Olson et al. 2012). In grain sorghum, from anthesis through grain maturity, canopies lack the whorl of leaves with small angles. As such, we expect that the potential effects of leaf angles on yield will vary depending on the duration of developmental phases of the crop.

This study identified significant genetic variation for leaf angle in sorghum germplasm that can be deployed in energy, forage, and grain sorghum breeding programs. The simulation and field results support the conclusion that smaller leaf inclination angles cause a redistribution of solar radiation in closed canopies resulting in greater photosynthetic conversion efficiency and greater biomass yield potential. Large-scale studies of energy sorghum hybrids differing in leaf angles will be required to determine the extent to which this trait can increase biomass yield under field conditions.