Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jun 26;5:11472. doi: 10.1038/srep11472

Extrinsic Origin of Persistent Photoconductivity in Monolayer MoS2 Field Effect Transistors

Yueh-Chun Wu 1,*, Cheng-Hua Liu 1,2,*, Shao-Yu Chen 1,†, Fu-Yu Shih 1,2, Po-Hsun Ho 3, Chun-Wei Chen 3, Chi-Te Liang 2, Wei-Hua Wang 1,a
PMCID: PMC4650635  PMID: 26112341

Abstract

Recent discoveries of the photoresponse of molybdenum disulfide (MoS2) have shown the considerable potential of these two-dimensional transition metal dichalcogenides for optoelectronic applications. Among the various types of photoresponses of MoS2, persistent photoconductivity (PPC) at different levels has been reported. However, a detailed study of the PPC effect and its mechanism in MoS2 is still not available, despite the importance of this effect on the photoresponse of the material. Here, we present a systematic study of the PPC effect in monolayer MoS2 and conclude that the effect can be attributed to random localized potential fluctuations in the devices. Notably, the potential fluctuations originate from extrinsic sources based on the substrate effect of the PPC. Moreover, we point out a correlation between the PPC effect in MoS2 and the percolation transport behavior of MoS2. We demonstrate a unique and efficient means of controlling the PPC effect in monolayer MoS2, which may offer novel functionalities for MoS2-based optoelectronic applications in the future.

Following the discovery of graphene1,2,3, two-dimensional (2D) materials have emerged as one of the most important research topics in condensed matter physics because of the novel phenomena exhibited by and the promising applications of these materials4,5,6. In particular, semiconducting layered materials7,8, such as transition metal dichalcogenides (TMD)9,10, can complement graphene because of their intrinsic bandgap and therefore can enrich the properties of these 2D materials11,12. Molybdenum disulfide (MoS2) is a layered semiconducting TMD and therefore exhibits a bandgap13,14, high mobility15,16 and strong mechanical properties17. Moreover, unique physical properties, including spin-valley coupling and the layer dependence of the band structure in MoS2, have been demonstrated18,19,20. The combination of these interesting properties has made MoS2 very attractive for new functionalities such as sensors21,22,23, logic circuits24,25 and optoelectronic devices26,27,28,29,30.

Recently, high photoresponsivity31,32, the photovoltaic effect29 and the photothermoelectric effect28. have been reported in monolayer MoS2-based photodetectors and phototransistors. Optoelectronic studies on these MoS2 devices demonstrated persistent photoconductivity (PPC), which is sustained conductivity after illumination is terminated32,33,34,35. However, a detailed understanding of PPC and its mechanism in MoS2 is still not available. The origin of the trap states in MoS2, which lead to the PPC effect, remains under debate36,37,38,39. Moreover, the PPC effect modifies the transport properties of MoS2 samples, which are sensitive to the history of photon irradiation. Therefore, it is essential to understand the PPC effect to control transport phenomena in MoS2.

Here, we present a systematic study of PPC in monolayer MoS2 field effect transistors. The PPC dependence on the temperature, the photon dose, and the excitation energy enabled us to attribute the PPC in MoS2 to random localized potential fluctuations that hinder the recombination of photoexcited electron-hole pairs. Comparing the PPC in suspended and substrate-supported MoS2 devices led us to conclude that PPC originates primarily from extrinsic sources. Moreover, we could correlate PPC phenomena with percolation transport, whereby carriers transfer among nearest low-potential puddles.

Details on the fabrication of the MoS2 field effect transistors can be found in the Supporting Information S1. In brief, we mechanically exfoliated MoS2 flakes onto an octadecyltrichlorosilane (OTS)-functionalized SiO2/Si substrate, thus obtaining a hydrophobic surface that minimized the amount of charged impurities in the 2D materials40. Monolayer MoS2 flakes were identified by optical microscopy and subsequently confirmed using Raman spectroscopy and photoluminescence (PL) measurements (Supporting Information S1). We deposited electrical contacts (Au, 50 nm) in a two-probe geometry using a residue-free approach41,42 to minimize contamination from the conventional lithography process. The MoS2 samples were stored under vacuum for 12 hours before performing the measurements to reduce the number of adsorbed molecules (Supporting Information S2). This procedure enabled us to investigate the photoresponse of MoS2 without interference from the gas adsorbate effect35.

Results and Discussion

Figure 1a shows the two-probe transconductance of sample A as a function of the back-gate voltage (G − VG). The MoS2 device exhibited typical n-type channel characters with a mobility of 0.7 cm2/Vs and an on/off ratio of 2 × 104. The MoS2 transistor was then illuminated by a laser (wavelength = 532 nm) with a spot size of ≃1.5 μm. After the illumination was terminated, the conductance of the device was greatly enhanced and remained in a high-conductivity state for a time period from 2 minutes to 2 hours, depending on the irradiated photo-dose. It is noted that the longer the illumination time, the higher was the conductance.

Figure 1. The PPC effect in a monolayer MoS2 transistor.

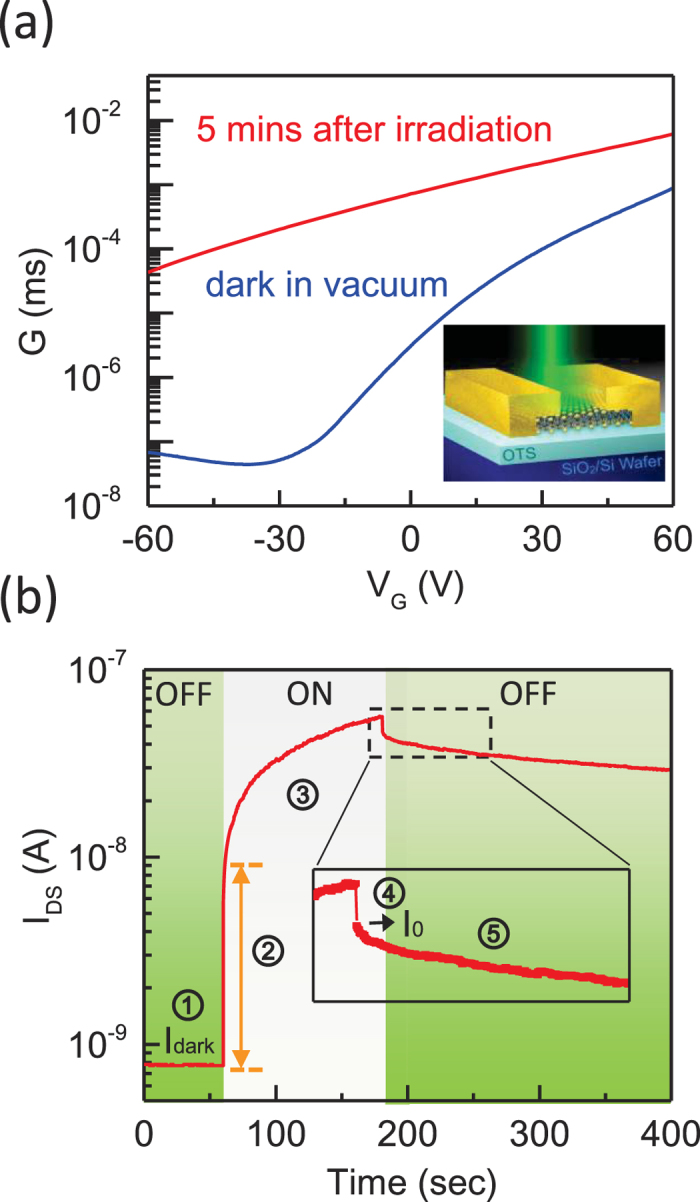
Figure 1

Open in a new tab

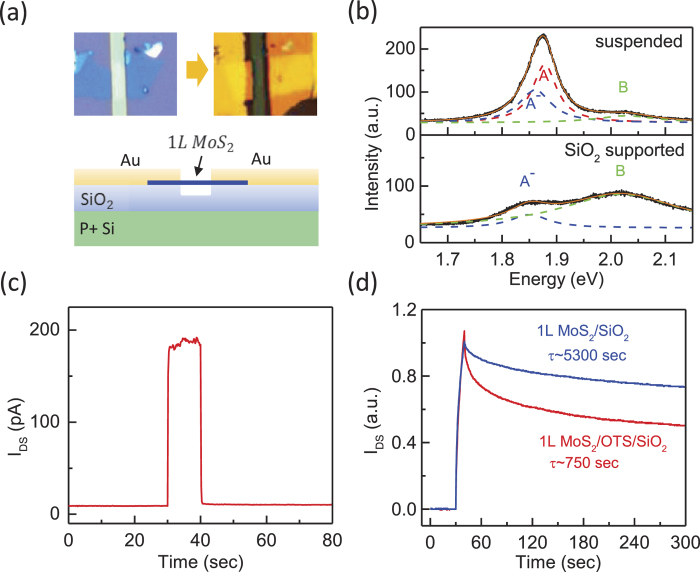
(a) Transconductance as a function of VG in the dark and after illumination at room temperature in vacuum, showing that the conductance of the device is greatly enhanced after illumination and remains in a high-conductivity state for a long period of time. Inset: a schematic of a MoS2 device on an OTS-functionalized substrate. (b) The photoresponse of the MoS2 device for VG = 0V and VDS = 50 mV, which can be classified into 5 stages. In addition to the photoresponse due to band-to-band transition (stages 2 and 4), the device exhibits a slow increase in the photocurrent under illumination (stage 3) and the PPC effect (stage 5).

We subsequently investigated the PPC in the MoS2 transistor in greater detail. Figure 1b shows the temporal evolution of the source–drain current (IDS − t) in vacuum (Supporting Information S3). The fast response of the current (stage 2) was attributed to a band-to-band transition that created conducting electrons and holes26,27. After the initial upsurge from the dark current (Idark) level, the ISD increased gradually to over 2 orders of magnitude (stage 3) above the dark current. This slow increase in the ISD could not be attributed to the common band-to-band transition. After the laser irradiation was terminated, the ISD exhibited a rapid drop because of the band-to-band transition (stage 4), followed by noticeable PPC (stage 5). The photocurrent at which PPC began to dominate is denoted by I0. This PPC effect was consistently observed in all of our 10 MoS2 devices. For MoS2 under ambient conditions, a short photoresponse time below 1 sec has been previously reported26 and attributed to the presence of gas adsorbates35. However, adsorbates were not a significant factor in the present study because our MoS2 samples were treated in vacuum.

We first discuss the temperature dependence of PPC in the MoS2 devices, which provides important indications of the PPC mechanism43. Figure 2a is a comparison of three characteristic PPC relaxations for sample A at T = 80, 180, and 300 K. For purposes of comparison, the dark level was subtracted, and the PPC was normalized by I0. It is noted that the PPC was more pronounced at high temperatures, although the photocurrent relaxed very fast and the PPC was considerably weakened at low temperatures (Supporting Information S4). The temperature dependence of the PPC was measured by heating the samples up to room temperature, allowing the carriers to relax to equilibrium38,44, and then cooling the samples down in the dark to the target temperature. The PPC relaxation curves were well-fitted by a single stretched exponential decay45,

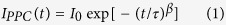graphic file with name srep11472-m1.jpg

where τ is the decay time constant, and β is the exponent (Supporting Information S5). The stretched exponential decay has been widely used to model relaxation processes in complex and slowly relaxing materials43,44,45,46. Therefore, this photocurrent decay suggests that PPC is related to disorders in the MoS2 devices.

Figure 2. The temperature dependence of PPC.

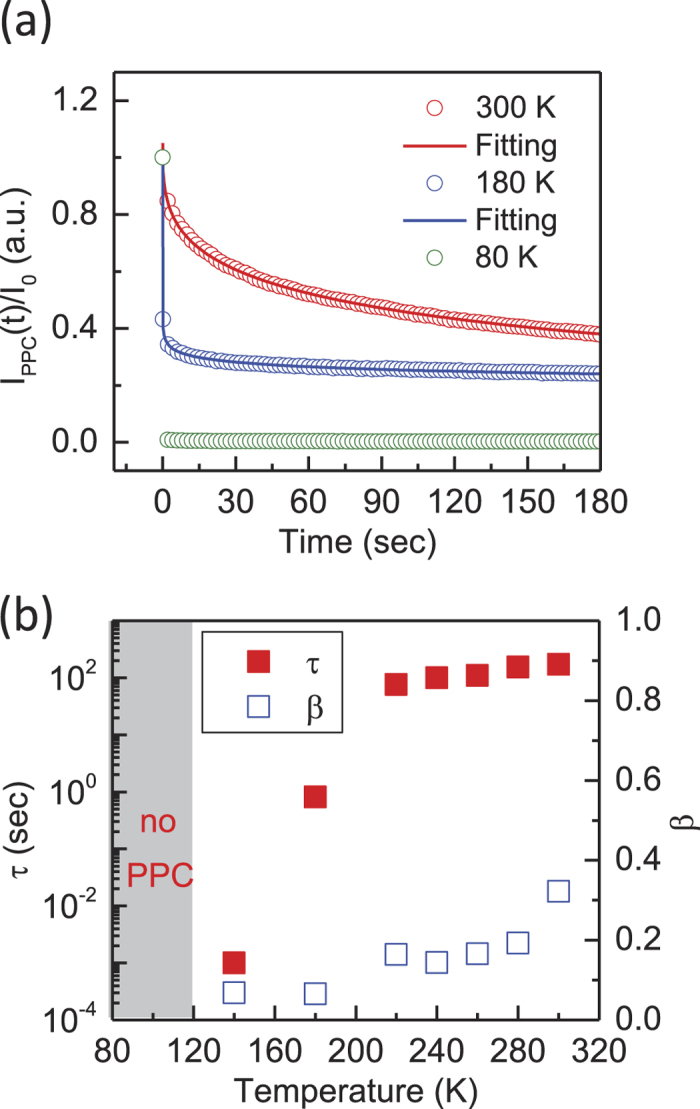
Figure 2

Open in a new tab

(a) Three characteristic PPC relaxations (circles) at T = 80, 180, and 300 K. PPC is more pronounced at higher temperatures but is greatly suppressed at T = 80 K. The PPC relaxations are well described by a stretched exponential decay (solid line). The stretched exponential decay is IPPC(t) = Ioexp[ – (t/τ)β] with the dark current subtracted. I0 in the PPC relaxation curves is normalized to 1 for comparison of the decay rate. (b) The temperature dependence of the decay time constant (τ) and the exponent (β). The grey region indicates the temperature range over which PPC is not observed.

The fitted τ and β values at different temperatures are shown in Fig. 2b. Clearly, the MoS2 device exhibited a shorter τ at low temperatures, which is a signature of the random local potential fluctuations (RLPF) model43,44. In the RLPF model, local potential fluctuations arise either because of intrinsic disorders in the materials or extrinsic charged impurities. Therefore, low-energy electrons and holes become localized in potential minima and are spatially separated, resulting in a long recombination lifetime. The thermal excitation of carriers to higher energy states above the mobility edge produces a photocurrent after the irradiation is terminated, resulting in the PPC effect. At low temperature, the carriers are well-confined inside charge traps and therefore, negligible PPC is observed. This RLPF model has been widely used to explain PPC in II-VI compound semiconductors43,44,46. However, this model has not been used to explain the PPC effect in 2D TMD materials.

The PPC in the MoS2 samples was attributed to the RLPF model in which the potential fluctuations originate from extrinsic36,47 or intrinsic48,49 sources. Extrinsic adsorbates or chemical impurities in the vicinity of the MoS2 samples can lead to trap states36,47. Alternatively, sulfur vacancies37 and the formation of MoO3 in bulk MoS2 have intrinsic causes. We determined the origin of the potential fluctuations by investigating the substrate effect on the PPC. We first measured the PPC in suspended MoS2 devices that were fabricated by exfoliating monolayer MoS2 onto SiO2/Si substrates with trenches (width ≃ 2 μm). Figure 3a shows the optical images of a fabricated suspended MoS2 device before and after deposition of the electrodes. To verify the suspension of the MoS2 sample, we measured the PL spectra of the sample, which are very sensitive to the existence of SiO2/Si substrates50. Figure 3b is a comparison of the PL spectra of a suspended MoS2 device (sample B) and a SiO2-supported MoS2. The PL spectrum of the suspended MoS2 exhibited a strong exciton peak (A), along with trion (A-) and exciton (B) peaks. The presence of the pronounced exciton peak A indicated that the MoS2 sample was free from the strong n-type doping effect of the SiO2 substrate50, indicating a suspended structure. In contrast, only trion (A-) and exciton (B) peaks were observed in the PL spectrum of SiO2-supported MoS2.

Figure 3. The substrate effect of PPC.

Figure 3

Open in a new tab

(a) Upper panel: optical images of the suspended MoS2 device before and after deposition of the electrode. Lower panel: a schematic of the suspended monolayer MoS2 device. (b) PL spectra of suspended (upper panel) and SiO2-supported (lower panel) monolayer MoS2 devices. (c) Photoresponse of the suspended MoS2 device showing negligible PPC at T = 300 K (VG = 0V, VDS = 5V). (d) Photoresponses of monolayer MoS2 on OTS-functionalized and conventional SiO2 substrates (VG = 0V, VDS = 5 V). The photocurrents are normalized by I0 for purposes of comparison.

Next, we discuss the photoresponse of the suspended MoS2 (sample B) that is shown in Fig. 3c. Interestingly, sample B exhibited a negligible PPC effect at T = 300 K, in contrast to the photoresponse of the substrate-supported MoS2 at the same temperature. Only the photoresponse from the band-to-band transition was observed in this suspended MoS2 device. The absence of the PPC effect in this control sample clearly indicated that the potential fluctuations in our MoS2 devices had extrinsic sources. We also compared the PPC effect for MoS2 devices that were fabricated on an OTS-functionalized SiO2 surface and those that were fabricated on conventional SiO2 substrates, as shown in Fig. 3d. The PPC effect in the MoS2/SiO2 device was stronger than that in the MoS2/OTS/SiO2 device. This substrate effect was consistently observed in several samples, suggesting that there were fewer charge traps in the MoS2/OTS/SiO2 devices than in the MoS2/SiO2 device. This difference was reasonable because the OTS-functionalized SiO2 surface is known to be hydrophobic and could therefore reduce surface adsorbates40, resulting in smaller potential variations. Further study is required to identify these extrinsic sources in detail, e.g., gas adsorbates and/or chemical impurities on the SiO2 interface. Nevertheless, our finding demonstrates the importance of extrinsic sources, thereby providing a means of eliminating the PPC effect to control the photoresponse in TMD materials.

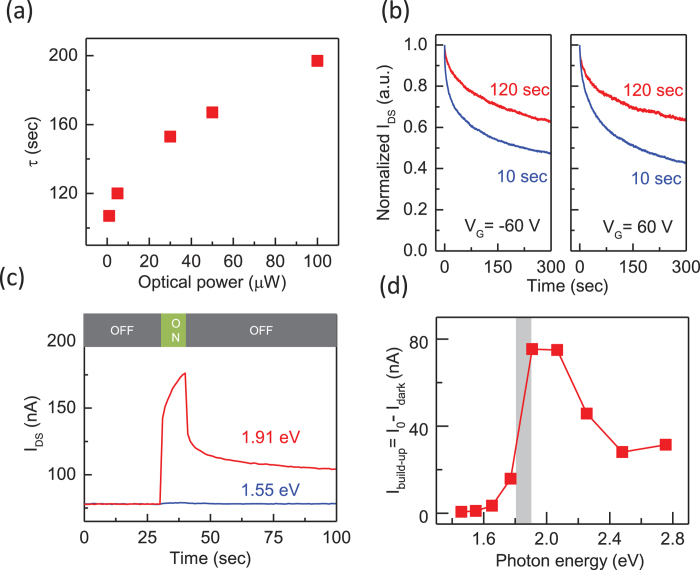
Next, we present the PPC dependence on the photon dose and the excitation energy to further validate the RLPF mechanism in our MoS2 samples. Figure 4a shows the excitation power dependence of τ at room temperature, where the PPC increases with the excitation power. In the RLPF model, more carriers are excited under higher photon doses, and more electrons and holes can redistribute to occupy the sites of the local potential minima. This redistribution of carriers is therefore enhanced under high excitation power, resulting in a larger τ after the photoexcitation is terminated46. Figure 4b shows the PPC relaxation for different illumination times at room temperature, where τ increases with the illumination time (Supporting Information S6), Similar to the effect of excitation power, this PPC dependence on the photon dose in MoS2 devices is in good agreement with the RLPF mechanism.

Figure 4. Photon dose and excitation wavelength dependences of the PPC relaxation.

Figure 4

Open in a new tab

(a) Excitation power dependence of the decay time constant for VG = –60 V and VDS = 50 mV. (b) The PPC relaxations for different illumination times (10 seconds and 120 seconds) at VG = ±60 V and VDS=50mV. (c) The temporal evolution of ISD for excitation energies below (Eex = 1.55 eV) and above (Eex = 1.91 eV) the bandgap at T = 300 K and VG = 0V. (d) The PPC build-up level (Ibuild-up) at different excited photon energies and VG = 0V. The photon dose and excitation energy dependences of the PPC are consistent with the RLPF model in the monolayer MoS2 devices.

We further investigated the PPC of monolayer MoS2 at different excitation energies ranging from 1.46 eV to 2.75 eV (Supporting Information S3), which included the optical bandgap in monolayer MoS2 ≃1.8 eV13,14. Figure 4c is a comparison of the temporal evolution of the photoresponse for excitation energies below (Eex = 1.55 eV) and above (Eex = 1.91 eV) the bandgap. While the IDS − t curve for Eex = 1.91 eV exhibited a typical photoresponse (which is similar to that in Fig. 1b), the photoresponse was insignificant for Eex = 1.55 eV. Figure 4d shows the excitation energy dependence of the PPC build-up level (Ibuild-up), which is defined as I0–Idark. Here, Ibuild-up represents the charging process in which photoexcited carriers fill up the local potential minimum during illumination. The photoresponse was clearly activated at Eex ~ 1.8 eV, showing that the bandgap of monolayer MoS2 is related to the PPC51. In the RLPF model, Ibuild-up is initiated by the photoexcited carriers through the band-to-band transition, which are subsequently confined by the trap states. Therefore, PPC can only occur when the photon energy surpasses the bandgap. To briefly summarize, our observations of the PPC dependence on the temperature, the substrate effect, the photon dose, and the excitation energy fully support the RLPF model as the mechanism of PPC in the monolayer MoS2 devices.

In addition to RLPF, two other mechanisms, large lattice relaxation (LLR)52,53 and the microscopic barrier (MB)54,55, are well-known mechanisms for PPC in a variety of materials, including mixed crystals, semiconductors, and heterostructures. In the LLR model, electrons are photoexcited from deep-level traps, and an energy barrier prevents the recapture of the electrons52,56, resulting in the PPC effect. Because the recapture is a thermally activated process, the PPC due to LLR is more pronounced at low temperatures, which is inconsistent with our observations (Fig. 2). Another feature of the PPC that results from LLR is that a photocurrent can be activated by excitation from deep-level traps to conduction bands57 with energies below that of the bandgap, which also contradicts the observed dependence of the PPC on the excitation energy. The MB is another mechanism for PPC in which photoexcited electron–hole pairs are spatially separated by a macroscopic potential barrier, followed by charge accumulation or trapping by barriers/spacers54,55. Recent studies on various structures, including MoS2/graphene30, quantum-dot/graphene58 and chlorophyll/graphene59 heterostructures, demonstrated noticeable PPC due to this MB model. However, there were no such artificially created structures in our MoS2 devices that could yield a macroscopic potential barrier. The PPC effect in the MB model also follows a single-exponential decay54, unlike the stretched exponential decay that was observed in our samples. We therefore conclude from our experimental data that LLR and MB are not mechanisms for PPC in our MoS2 devices.

Finally, we consider the connection between the PPC effect and the transport properties of the MoS2 devices. Figure 5a is an Arrhenius plot of the conductance of sample C at different 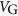Inline graphic values and shows that insulating behavior (dG/dT > 0) was found over the temperature range 80 < T < 300 K. For T > 200 K, the MoS2 sample exhibited thermally activated behavior, where the activation energy was extracted from the linear fit (Ea = 98 meV at VG = 0 V). The carrier transport in this temperature regime could be described by a percolation model, in which conduction occurs via a network of spatially distributed charge puddles60. The activation energy then corresponded to the average potential barrier of the charge puddles. For 80 K < T < 200 K, the correlation of the puddles decreased because of the decrease in the thermal energy, and the carriers could only conduct by tunneling between localized states60. Therefore, there was a phase transition from localized to percolation transport. The transition temperature of sample C was TC ~ 200 K, which corresponded to the temperature at which the G–1/T curve deviated from thermally activated behavior (more details are provided in Supporting Information S7). To compare the temperature dependence of the PPC and transport properties, we plot Ibuild-up as a function of temperature in Fig. 5b. The PPC is insignificant for T < 200 K because of the low conductivity in the localized transport regime. Notably, Ibuild-up exhibited an activated behavior for T > 200 K, where the transition temperature coincided with the TC value that was extracted from the transport behavior. Ibuild-up could be described by a percolation approach43:

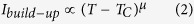graphic file with name srep11472-m3.jpg

where μ is the characteristic exponent. We found that this function fits the data reasonably well (μ = 2.6), indicating that the PPC relaxation was consistent with the percolation transport picture.

Figure 5. Correlations between PPC and transport behaviors.

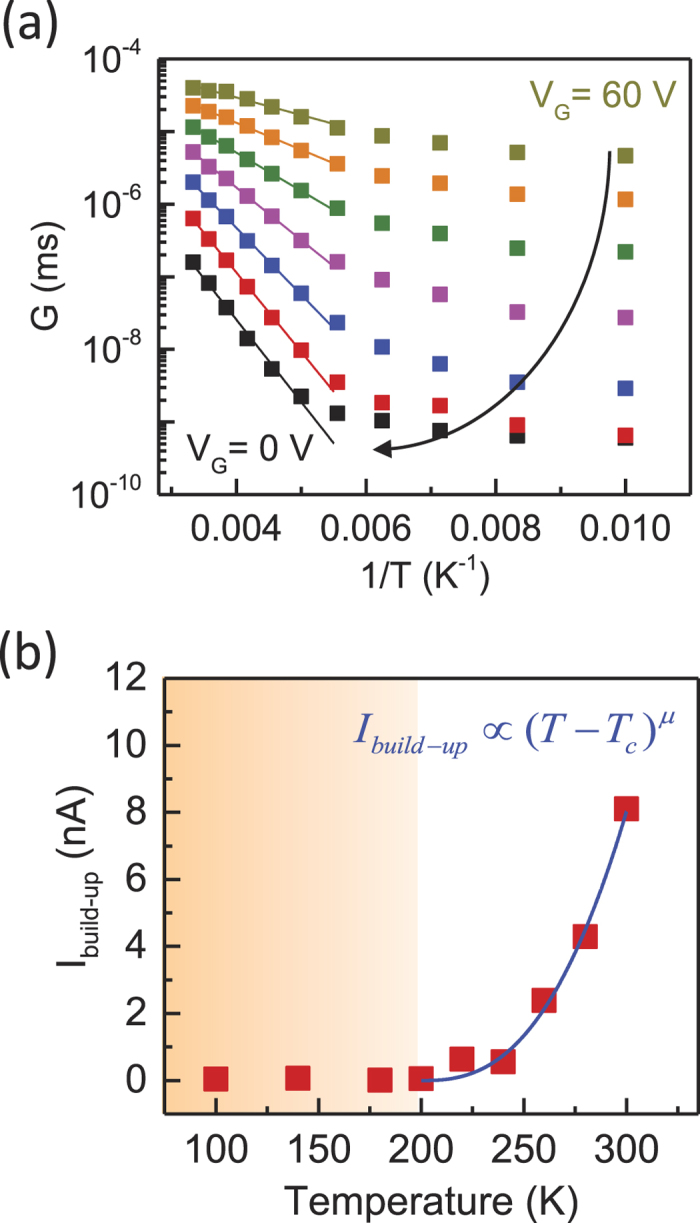
Figure 5

Open in a new tab

(a) The Arrhenius plot for the conductance of sample C at different VG values. The solid lines indicate linear fits in the thermally activated regime. (b) The temperature dependence of the PPC buildup level (Ibuild-up) at VG = 0V. For T > 200 K, Ibuild-up is well described by a percolation model, which is shown as a solid line. The shaded region denotes the temperature regime over which transport is dominated by tunneling between localized states.

In conclusion, we have demonstrated that PPC in monolayer MoS2 can be controlled by temperature, the photon dose, the excitation energy, and the substrate effect. These characteristics show that PPC in MoS2 can be well-explained by the RLPF model. The potential fluctuations could be attributed to extrinsic sources because of the absence of PPC in the suspended MoS2 devices. Moreover, the temperature dependence of the PPC could be described as a transition from localization to percolation models, which was in agreement with the transport properties of MoS2. The results of this study can provide insight into PPC phenomena in monolayer MoS2, which is important for the development of MoS2-based optoelectronic applications.

Methods

Sample preparation

MoS2 flakes (SPI Supplies) were mechanically exfoliated onto octadecyltrichlorosilane (OTS) self-assembled monolayer (SAM) functionalized SiO2 (300 nm)/Si substrates. The surface of the OTS-functionalized SiO2/Si substrate was hydrophobic with a typical contact angle above 110°. First, the MoS2 flakes were identified and characterized under an optical microscope using variations in contrast and then were examined by Raman and photoluminescence spectra. We adopted resist-free fabrication to prevent contamination of the MoS2 samples from the resist residue of the conventional lithography process. We used nanowire as a shadow mask to deposit metallic contacts (Au, 50 nm) with an electron-beam evaporator at a base pressure of 1.0 × 10–7 Torr. The MoS2 devices were then transferred into a cryostat (Janis Research Company, ST-500) for electrical and optical characterization. The samples were stored under a high vacuum of 1 × 10–6 Torr to minimize the undesirable adsorption of chemical substances. A Keithley 237 was used to perform the DC electrical measurements, and a Keithley 2400 was used to apply the back gate voltage.

Additional Information

How to cite this article: Wu, Y.-C. et al. Extrinsic Origin of Persistent Photoconductivity in Monolayer MoS2 Field Effect Transistors. Sci. Rep. 5, 11472; doi: 10.1038/srep11472 (2015).

Supplementary Material

Supplementary Information
srep11472-s1.pdf (843.9KB, pdf)

Acknowledgments

This work was supported by Academia Sinica and the Ministry of Science and Technology of Taiwan (Grant No. MOST 103-2112-M-001-020-MY3).

Footnotes

Author Contributions W.H.W. supervised the project. Y.C.W., C.H.L. and S.Y.C. designed the experiments. P.H.H. and C.W.C. provided the OTS-functionalized substrates. F.Y.S. provided the substrates for suspended samples. Y.C.W. and C.H.L. prepared the samples and carried out the photoresponse and transport measurements. Y.C.W., C.H.L. and S.Y.C. analyzed the data. W.H.W, Y.C.W., C.W.C. and C.T.L. wrote the paper. All authors discussed the results and contributed to the refinement of the paper.

References

  1. Novoselov K. S. et al. Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669, 10.1126/science.1102896 (2004). [DOI] [PubMed] [Google Scholar]
  2. Novoselov K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200, 10.1038/Nature04233 (2005). [DOI] [PubMed] [Google Scholar]
  3. Zhang Y., Tan Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204, (2005). [DOI] [PubMed] [Google Scholar]
  4. Novoselov K. S. et al. A roadmap for graphene. Nature 490, 192–200 (2012). [DOI] [PubMed] [Google Scholar]
  5. Butler S. Z. et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. Acs Nano 7, 2898–2926, 10.1021/Nn400280c (2013). [DOI] [PubMed] [Google Scholar]
  6. Huang X., Qi X. Y., Boey F. & Zhang H. Graphene-based composites. Chem. Soc. Rev. 41, 666–686, 10.1039/C1cs15078b (2012). [DOI] [PubMed] [Google Scholar]
  7. Novoselov K. S. et al. Two-dimensional atomic crystals. Proceedings of the National Academy of Sciences of the United States of America 102, 10451–10453, 10.1073/pnas.0502848102 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Coleman J. N. et al. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 331, 568–571, 10.1126/science.1194975 (2011). [DOI] [PubMed] [Google Scholar]
  9. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-layer MoS2 transistors. Nat Nanotechnol 6, 147–150, 10.1038/Nnano.2010.279 (2011). [DOI] [PubMed] [Google Scholar]
  10. Podzorov V., Gershenson M. E., Kloc C., Zeis R. & Bucher E. High-mobility field-effect transistors based on transition metal dichalcogenides. Appl. Phys. Lett. 84, 3301–3303, 10.1063/1.17236395 (2004). [DOI] [Google Scholar]
  11. Geim A. K. & Grigorieva I. V. Van der Waals heterostructures. Nature 499, 419–425, 10.1038/Nature12385 (2013). [DOI] [PubMed] [Google Scholar]
  12. Wang Q. H., Kalantar-Zadeh K., Kis A., Coleman J. N. & Strano M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012). [DOI] [PubMed] [Google Scholar]
  13. Mak K. F., Lee C., Hone J., Shan J. & Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 105, 136805, Artn 136805; 10.1103/Physrevlett.105.136805 (2010). [DOI] [PubMed] [Google Scholar]
  14. Splendiani A. et al. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 10, 1271–1275, 10.1021/Nl903868w (2010). [DOI] [PubMed] [Google Scholar]
  15. Baugher B. W. H., Churchill H. O. H., Yang Y. F. & Jarillo-Herrero P. Intrinsic Electronic Transport Properties of High-Quality Monolayer and Bilayer MoS2. Nano Lett. 13, 4212–4216, 10.1021/Nl401916s (2013). [DOI] [PubMed] [Google Scholar]
  16. Radisavljevic B. & Kis A. Mobility engineering and a metal–insulator transition in monolayer MoS2. Nat. Mater. 12, 815–820, 10.1038/nmat3687 (2013). [DOI] [PubMed] [Google Scholar]
  17. Castellanos-Gomez A. et al. Elastic Properties of Freely Suspended MoS2 Nanosheets. Adv. Mater. 24, 772–775, 10.1002/adma.201103965 (2012). [DOI] [PubMed] [Google Scholar]
  18. Mak K. F., He K., Shan J. & Heinz T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 494–498, (2012). [DOI] [PubMed] [Google Scholar]
  19. Xiao D., Liu G. B., Feng W. X., Xu X. D. & Yao W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 108, 196802, Artn 196802; 10.1103/Physrevlett.108.196802 (2012). [DOI] [PubMed] [Google Scholar]
  20. Zeng H., Dai J., Yao W., Xiao D. & Cui X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol. 7, 490–493, (2012). [DOI] [PubMed] [Google Scholar]
  21. He Q. et al. Fabrication of Flexible MoS2 Thin-Film Transistor Arrays for Practical Gas-Sensing Applications. Small 8, 2994–2999, 10.1002/smll.201201224 (2012). [DOI] [PubMed] [Google Scholar]
  22. Li H. et al. Fabrication of Single- and Multilayer MoS2 Film-Based Field-Effect Transistors for Sensing NO at Room Temperature. Small 8, 63–67, 10.1002/smll.201101016 (2012). [DOI] [PubMed] [Google Scholar]
  23. Zhu C. F. et al. Single-Layer MoS2-Based Nanoprobes for Homogeneous Detection of Biomolecules. J. Am. Chem. Soc. 135, 5998–6001, 10.1021/Ja4019572 (2013). [DOI] [PubMed] [Google Scholar]
  24. Radisavljevic B., Whitwick M. B. & Kis A. Integrated Circuits and Logic Operations Based on Single-Layer MoS2. Acs Nano 5, 9934–9938, 10.1021/nn203715c (2011). [DOI] [PubMed] [Google Scholar]
  25. Wang H. et al. Integrated Circuits Based on Bilayer MoS2 Transistors. Nano Lett. 12, 4674–4680, 10.1021/nl302015v (2012). [DOI] [PubMed] [Google Scholar]
  26. Yin Z. Y. et al. Single-Layer MoS2 Phototransistors. ACS Nano 6, 74–80, 10.1021/Nn2024557 (2012). [DOI] [PubMed] [Google Scholar]
  27. Lee H. S. et al. MoS2 Nanosheet Phototransistors with Thickness-Modulated Optical Energy Gap. Nano Lett. 12, 3695–3700, 10.1021/Nl301485q (2012). [DOI] [PubMed] [Google Scholar]
  28. Buscema M. et al. Large and Tunable Photothermoelectric Effect in Single-Layer MoS2. Nano Lett. 13, 358–363, 10.1021/nl303321g (2013). [DOI] [PubMed] [Google Scholar]
  29. Fontana M. et al. Electron-hole transport and photovoltaic effect in gated MoS2 Schottky junctions. Sci. Rep. 3 1634 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Roy K. et al. Graphene-MoS2 hybrid structures for multifunctional photoresponsive memory devices. Nat Nanotechnol 8, 826–830, 10.1038/Nnano.2013.206 (2013). [DOI] [PubMed] [Google Scholar]
  31. Lopez-Sanchez O., Lembke D., Kayci M., Radenovic A. & Kis A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 8, 497–501, 10.1038/nnano.2013.100 (2013). [DOI] [PubMed] [Google Scholar]
  32. Zhang W. et al. High-Gain Phototransistors Based on a CVD MoS2 Monolayer. Adv. Mater. 25, 3456–3461, 10.1002/adma.201301244 (2013). [DOI] [PubMed] [Google Scholar]
  33. Lopez-Sanchez O., Lembke D., Kayci M., Radenovic A. & Kis A. Ultrasensitive photodetectors based on monolayer MoS2. Nat Nanotechnol 8, 497–501, 10.1038/Nnano.2013.100 (2013). [DOI] [PubMed] [Google Scholar]
  34. Cunningham G. et al. Photoconductivity of solution-processed MoS2 films. J Mater Chem C 1, 6899–6904, 10.1039/C3tc31402b (2013). [DOI] [Google Scholar]
  35. Cho K. et al. Gate-bias stress-dependent photoconductive characteristics of multi-layer MoS2 field-effect transistors. Nanotechnology 25, 155201, Artn 155201; 10.1088/0957-4484/25/15/155201 (2014). [DOI] [PubMed] [Google Scholar]
  36. Ghatak S., Pal A. N. & Ghosh A. Nature of Electronic States in Atomically Thin MoS2 Field-Effect Transistors. Acs Nano 5, 7707–7712, 10.1021/Nn202852j (2011). [DOI] [PubMed] [Google Scholar]
  37. Qiu H. et al. Hopping transport through defect-induced localized states in molybdenum disulphide. Nat. Commun. 4, 10.1038/ncomms3642 (2013). [DOI] [PubMed] [Google Scholar]
  38. Zhu W. et al. Electronic transport and device prospects of monolayer molybdenum disulphide grown by chemical vapour deposition. Nat. Commun. 5, 10.1038/ncomms4087 (2014). [DOI] [PubMed] [Google Scholar]
  39. Ghatak S. & Ghosh A. Observation of trap-assisted space charge limited conductivity in short channel MoS2 transistor. Appl. Phys. Lett. 103, 122103-1–122103-4, Artn 122103; 10.1063/1.4821185 (2013). [DOI] [Google Scholar]
  40. Chen S.-Y., Ho P.-H., Shiue R.-J., Chen C.-W. & Wang W.-H. Transport/Magnetotransport of High-Performance Graphene Transistors on Organic Molecule-Functionalized Substrates. Nano Lett. 12, 964–969, 10.1021/nl204036d (2012). [DOI] [PubMed] [Google Scholar]
  41. Cheng H.-C., Shiue R.-J., Tsai C.-C., Wang W.-H. & Chen Y.-T. High-Quality Graphene p−n Junctions via Resist-free Fabrication and Solution-Based Noncovalent Functionalization. Acs Nano 5, 2051–2059, 10.1021/nn103221v (2011). [DOI] [PubMed] [Google Scholar]
  42. Shih F. Y. et al. Residue-free fabrication of high-performance graphene devices by patterned PMMA stencil mask. Aip Adv 4, 067129-1–067129-6, Artn 067129; 10.1063/1.4884305 (2014). [DOI] [Google Scholar]
  43. Jiang H. X. & Lin J. Y. Percolation transition of persistent photoconductivity in II-VI mixed crystals. Phys Rev Lett 64, 2547–2550, 10.1103/PhysRevLett.64.2547 (1990). [DOI] [PubMed] [Google Scholar]
  44. Jiang H. X. & Lin J. Y. Persistent Photoconductivity and Related Critical Phenomena in Zn0.3cd0.7se. Phys Rev B 40, 10025–10028, 10.1103/PhysRevB.40.10025 (1989). [DOI] [PubMed] [Google Scholar]
  45. Palmer R. G., Stein D. L., Abrahams E. & Anderson P. W. Models of Hierarchically Constrained Dynamics for Glassy Relaxation. Phys. Rev. Lett. 53, 958–961 (1984). [Google Scholar]
  46. Dissanayake A. S., Huang S. X., Jiang H. X. & Lin J. Y. Charge Storage and Persistent Photoconductivity in a Cds0.5se0.5 Semiconductor Alloy. Phys Rev B 44, 13343–13348, 10.1103/PhysRevB.44.13343 (1991). [DOI] [PubMed] [Google Scholar]
  47. Lu C. P., Li G. H., Mao J. H., Wang L. M. & Andrei E. Y. Bandgap, Mid-Gap States, and Gating Effects in MoS2. Nano Lett. 14, 4628–4633, 10.1021/Nl501659n (2014). [DOI] [PubMed] [Google Scholar]
  48. McDonnell S., Addou R., Buie C., Wallace R. M. & Hinkle C. L. Defect-Dominated Doping and Contact Resistance in MoS2. Acs Nano 8, 2880–2888, 10.1021/Nn500044q (2014). [DOI] [PubMed] [Google Scholar]
  49. Ghatak S., Mukherjee S., Jain M., Sarma D. & Ghosh A. Microscopic Origin of Charged Impurity Scattering and Flicker Noise in MoS2 field-effect Transistors. arXiv preprint arXiv :1403.3333 (2014). [Google Scholar]
  50. Scheuschner N. et al. Photoluminescence of freestanding single- and few-layer MoS2. Phys Rev B 89, 125406-1–125406-6, Artn 125406; 10.1103/Physrevb.89.125406 (2014). [DOI] [Google Scholar]
  51. Wu C.-C. et al. Elucidating the Photoresponse of Ultrathin MoS2 Field-Effect Transistors by Scanning Photocurrent Microscopy. J. Phys. Chem. Lett. 4, 2508–2513, 10.1021/jz401199x (2013). [DOI] [Google Scholar]
  52. Lang D. V. & Logan R. A. Large-Lattice-Relaxation Model for Persistent Photoconductivity in Compound Semiconductors. Phys. Rev. Lett. 39, 635–639, 10.1103/PhysRevLett.39.635 (1977). [DOI] [Google Scholar]
  53. Lang D. V., Logan R. A. & Jaros M. Trapping Characteristics and a Donor-Complex (Dx) Model for the Persistent Photoconductivity Trapping Center in Te-Doped AlxGa1-XAs. Phys Rev B 19, 1015–1030, 10.1103/PhysRevB.19.1015 (1979). [DOI] [Google Scholar]
  54. Queisser H. J. & Theodorou D. E. Decay kinetics of persistent photoconductivity in semiconductors. Phys. Rev. B 33, 4027–4033 (1986). [DOI] [PubMed] [Google Scholar]
  55. Theis T. N. & Wright S. L. Origin of Residual Persistent Photoconductivity in Selectively Doped GaAs/AlxGa1-XAs Heterojunctions. Appl. Phys. Lett. 48, 1374–1376, 10.1063/1.97028 (1986). [DOI] [Google Scholar]
  56. Nelson R. J. Long-Lifetime Photoconductivity Effect in N-Type GaAlAs. Appl. Phys. Lett. 31, 351–353, 10.1063/1.89696 (1977). [DOI] [Google Scholar]
  57. Lee Y. C. et al. Observation of persistent photoconductivity in 2H‐MoSe2 layered semiconductors. J. Appl. Phys. 99, 063706-1–063706-4, (2006). [Google Scholar]
  58. Konstantatos G. et al. Hybrid graphene-quantum dot phototransistors with ultrahigh gain. Nat. Nanotechnol. 7, 363–368, (2012). [DOI] [PubMed] [Google Scholar]
  59. Chen S.-Y. et al. Biologically inspired graphene-chlorophyll phototransistors with high gain. Carbon 63, 23–29, (2013). [Google Scholar]
  60. Lo S. T. et al. Transport in disordered monolayer MoS2 nanoflakes-evidence for inhomogeneous charge transport. Nanotechnology 25, 375201-1–375201-8, Artn 375201; 10.1088/0957-4484/25/37/375201 (2014). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep11472-s1.pdf (843.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES