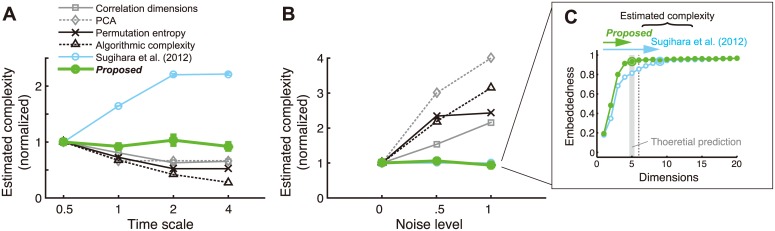
Fig 2. Cross-embedding with random coordinates dissociates interaction-relevant complexity from timescale or noise variations.

(A) Complexity estimates based on embedding y with x in the system used in Fig 1C–1F, where timescale of signal was varied. The estimates with each method were shown as relative values to those at timescale = 0.5. The results were similar in embedding x with y. (B) The results where the observation noise level was varied. The noise level corresponds to the standard deviation of the (zero-mean) normal distribution, from which noise were generated. The results are shown as relative values to those at noise level = 0. Although both the standard- and random-coordinate embedding methods (circle symbols) are invariant to noise level in terms of the relative values, the random-coordinate method estimates the true complexity more accurately in absolute values (see panel C). (C) Coordinate randomization avoids overestimation of complexity. The markers and error bars indicate the averages ±s.e.m. across 10 trials with different initial states of dynamics. Here, the pre-normalized complexity estimates using regular delay coordinates, (x _t, x _t-τ …) (open symbols), are compared with results in Fig 1C (y embedded by x) which used random delay coordinates (closed symbols); other conventions follows those in Fig 1F. The theoretically predicted embedding dimension of x (shaded bar) were accurately estimated using random coordinates, while the previous method using standard delay-coordinates tends to overestimate it, even exceeding the total number of nodes (dotted line) in the simulated system, which upper bounds the theoretically possible attractor dimensions by construction.