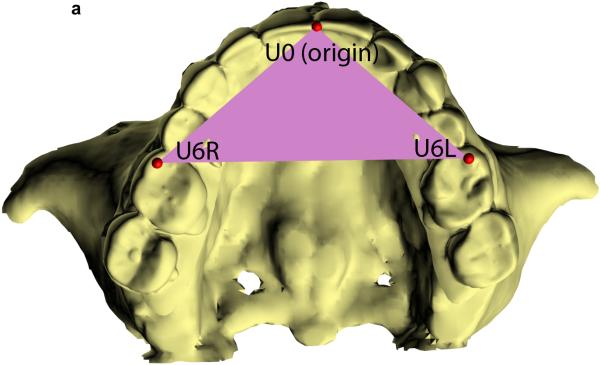
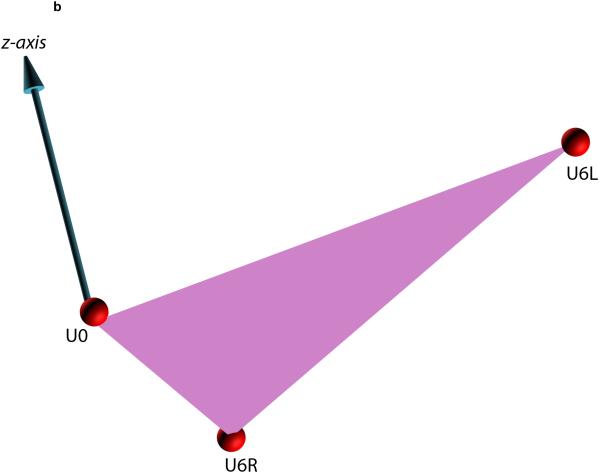
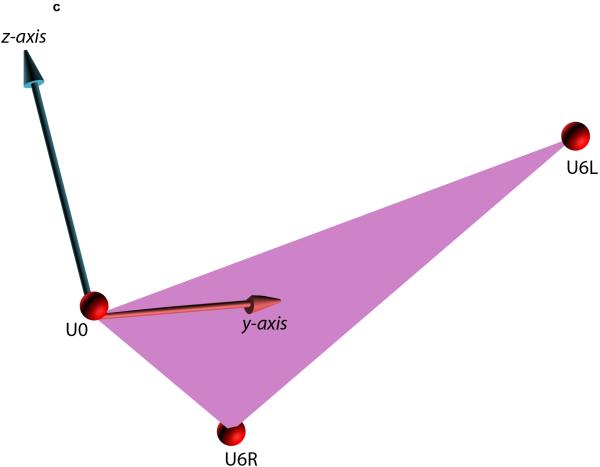
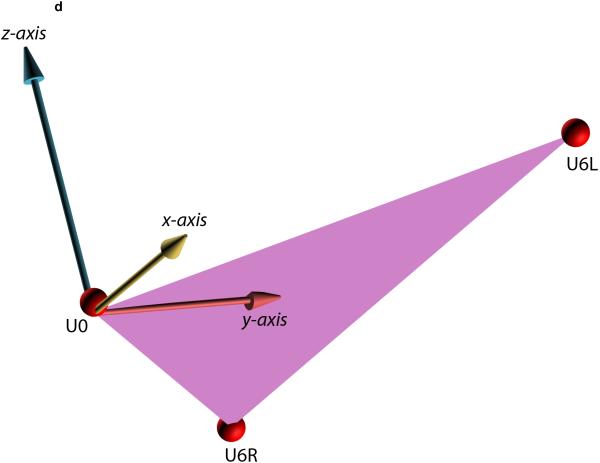
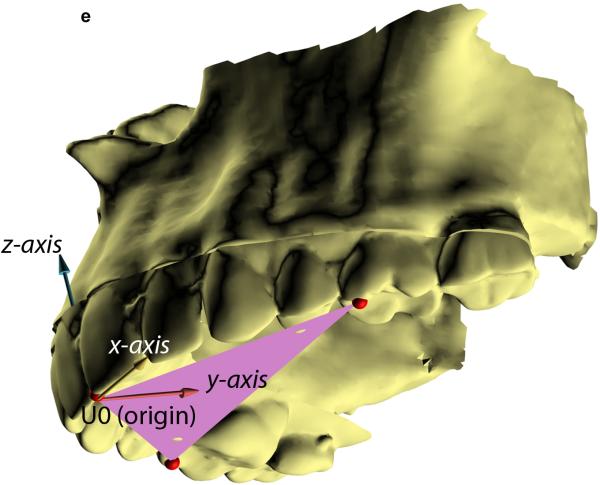
Fig. 2.
Defining the local coordinate system for a facial unit using the triangular method. This example illustrates how the triangular method is completed for the maxilla. (A) In the first step, a maxillary occlusal plane is defined by three points: right mesiobuccal cusp (U6R), left mesiobuccal cusp (U6L), and central dental midline (U0). U0 is used as the origin of the maxillary local coordinate system. (B) In the second step, the computer calculates a normal vector for this plane. This vector represents the vertical (z) axis of the local coordinate system. (C) In the third step, the computer calculates the local anteroposterior (y) axis. This axis passes through U0 and bisects a line that goes from U6R to U6L. (D) In the last step, the computer calculates the transverse (x) axis of the local coordinate system. This axis is perpendicular to z and y axes. (E) 3D view of the maxillary local coordinate system.