Filming the formation and fluctuation of skyrmion domains by cryo-Lorentz transmission electron microscopy

Significance

The need for denser storage devices calls for new materials and nanostructures capable of confining single bits of information in a few nanometers. A new topological distribution of spins termed skyrmions is emerging, which promises to robustly confine a small magnetization in a few-nanometers-wide circular domain. A great deal of attention is being devoted to the understanding of these magnetic patterns and their manipulation. We manufactured a large nanoslice supporting over 70,000 skyrmions, and film their evolution in direct-space via cryo-Lorentz transmission electron microscopy. We reveal the octagonal distortion of the skyrmion lattice and show how these distortions and other defects impact its long-range order. These results pave the way to the control of a large two-dimensional array of skyrmions.

Abstract

Magnetic skyrmions are promising candidates as information carriers in logic or storage devices thanks to their robustness, guaranteed by the topological protection, and their nanometric size. Currently, little is known about the influence of parameters such as disorder, defects, or external stimuli on the long-range spatial distribution and temporal evolution of the skyrmion lattice. Here, using a large ($7.3\times 7.3\mu {\text{m}}^2$) single-crystal nanoslice (150 nm thick) of Cu₂OSeO₃, we image up to 70,000 skyrmions by means of cryo-Lorentz transmission electron microscopy as a function of the applied magnetic field. The emergence of the skyrmion lattice from the helimagnetic phase is monitored, revealing the existence of a glassy skyrmion phase at the phase transition field, where patches of an octagonally distorted skyrmion lattice are also discovered. In the skyrmion phase, dislocations are shown to cause the emergence and switching between domains with different lattice orientations, and the temporal fluctuation of these domains is filmed. These results demonstrate the importance of direct-space and real-time imaging of skyrmion domains for addressing both their long-range topology and stability.

In a noncentrosymmetric chiral lattice, the competition between the symmetric ferromagnetic exchange, the antisymmetric Dzyaloshinskii–Moriya interaction, and an applied magnetic field can stabilize a highly ordered spin texture, presenting as a hexagonal lattice of spin vortices called skyrmions (1–4).

Magnetic skyrmions have been experimentally detected in materials having the B20 crystal structure such as MnSi (5), ${\mathrm{Fe}}_{1-x}$Co_xSi (6, 7), FeGe (8), and Cu₂OSeO₃ (9) and, recently, also on systems like GaV₄S₈ (10) and beta-Mn-type alloys (11). Small-angle neutron scattering studies of bulk solids evidenced the formation of a hexagonal skyrmion lattice confined in a very narrow region of temperature and magnetic field (T-B) in the phase diagram (5, 6). In thin films and thinly cut slices of the same compounds, instead, skyrmions can be stabilized over a wider T-B range as revealed by experiments using cryo-Lorentz transmission electron microscopy (LTEM) (12, 13). Furthermore, it was proposed and recently observed that skyrmions can also exist as isolated objects before the formation of the ordered skyrmion lattice (14, 15). A recent resonant X-ray diffraction experiment also suggested the formation of two skyrmion sublattices giving rise to regular superstructures (16).

In a 2D landscape, long-range ordering can be significantly altered by the presence of defects and disorder. Indeed, the competition between order and disorder within the context of lattice formation continues to be an issue of fundamental importance. Condensed matter systems are well known to provide important test beds for exploring theories of structural order in solids and glasses. An archetypal and conceptually relevant example is the superconducting vortex lattice, where real-space imaging studies allow direct access to the positional correlations and local coordination numbers (17–19). Up until now, however, analogous studies of skyrmion lattices have not been reported even though (as for superconducting vortices) it is well known that defects and dislocations present in a sample can pin the motion of skyrmions induced by external perturbations such as an electric field (20) or a magnetic field (16). This competition between disorder and elasticity will clearly give rise to a complex energy landscape promoting diverse metastable states (21) and superstructures (22, 23). Furthermore, previous imaging studies of skyrmion lattices could probe only the short-range order due to limitations in the size of the imaged area and its homogeneity.

In this paper, by systematic observations using cryo-LTEM, we reveal the magnetic field-dependent evolution of the skyrmion-related spin textures in a Cu₂OSeO₃ thin plate and study their long-range ordering properties imaging up to ∼1,000 lattice constants. The different phases of the spin textures are analyzed with state-of-the-art methods to unravel their spatial properties. At low magnetic fields, the coexistence of two helical domains is observed, in contrast to previous studies (9); the angle between the two helices’ axis is retrieved via a reciprocal space analysis. At the magnetic field close to the helical–skyrmion phase transition, evidence for a glassy skyrmion phase is found via cross-correlation analysis, a method that has recently been applied to the analysis of both X-rays and electron diffraction patterns to retrieve information on the local order and symmetry of colloidal systems (24–26). In this phase, we reveal also patches of octagonally distorted skyrmion lattice crystallites. In the skyrmion phase, by locating the position of each skyrmion and generating an angle map of the hexagonal unit cell they formed, we obtain a direct-space distortion map of the skyrmion lattice. This distortion map evidences the presence of orientation-disordered skyrmion lattice domains present within the single-crystalline sample. Each domain boundary coincides with a dislocation formed by a seven–five or a five–eight–five Frenkel-type defect. The number of such dislocations decreases with increasing magnetic field, and large single-domain regions are formed. The formation of these mesoscopic domains was also filmed with camera-rate (millisecond) time resolution. The presence of differently oriented skyrmion lattice domains was observed in spatially separated regions, or in the same area of the sample but at a different moment in time. Based on our observation, we propose an alternative scenario for the appearance of split magnetic Bragg peaks reported in ref. 16. Instead of the formation of regular superstructures of coexisting misoriented skyrmion lattices in real space, we suggest that the splitting is caused by a spatial or temporal integration of an orientation-fluctuating skyrmion lattice. This result highlights the importance of a direct-space, real-time probe for assessing the dynamical topological properties of a large number of skyrmions.

Experimental Procedures

A flat and smooth single-crystalline Cu₂OSeO₃ plate was thinned to 150 nm by the Focused Ion Beam (FIB) technique (see Materials and Methods). The sample was prepared as a slice with uniform thickness instead of the wedge-shaped sample used in previous studies (27). This sample geometry prevents significant positional drift of skyrmions, as is indeed common for wedge-shaped samples due to thickness variations or a temperature gradient. The smoothness and homogeneity of our sample are corroborated by the thickness map shown in SI Appendix, Fig. S13. We capture more than 70,000 skyrmions and span their low-temperature phase diagram as a function of the external magnetic field. All images were recorded in the (111) sample plane, and the magnetic field was applied along the $\langle 111\rangle$ direction.

Results

Real- and Reciprocal-Space Maps of Different Phases.

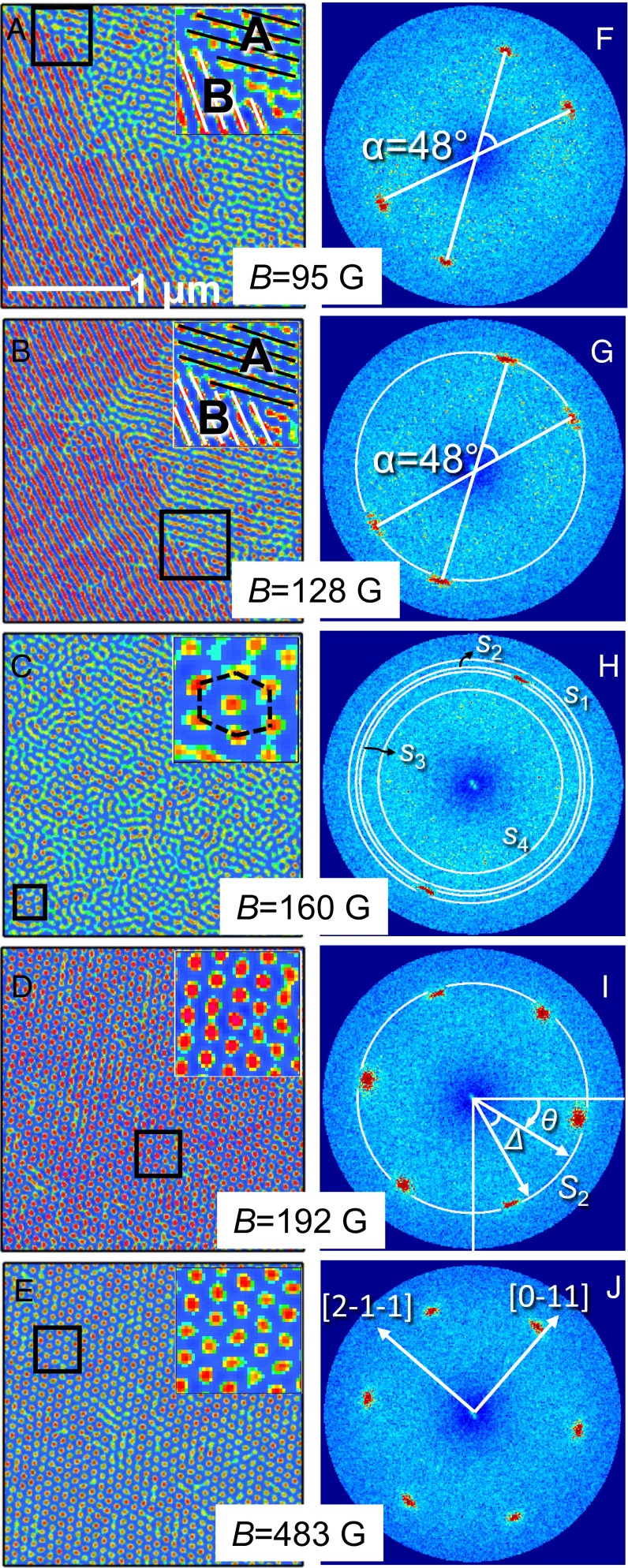
Cryo-Lorentz images at a temperature of $\text{T}\approx 7$ K and different magnetic fields are shown in Fig. 1 A–E. The images represent a $2.5\times 2.5$ μm² zoom of the total $7.3\times 7.3$ μm² micrograph. The images displayed are treated by a standard Fourier filtering algorithm for better visualization. However, all analyses were performed on the original images. The raw micrographs of the entire area imaged at all magnetic fields investigated are displayed in SI Appendix, Figs. S1–S7. A further zoom of the real-space image marked by the black solid square in each figure is shown in Fig. 1 A–E, Insets. Fig. 1 F–J depicts the reciprocal-space patterns obtained from the corresponding whole and unfiltered real-space image. Every 2D Fourier Transform (FT) is displayed up to a scattering vector $s=12\times {10}^{-3}{\text{Å}}^{-1}$ for clarity. Our FT procedure is explained in detail in SI Appendix, where the full 2D FTs obtained from each $7.3\times 7.3$ μm² micrograph are displayed as well.

Fig. 1.

Magnetic field dependence of the lateral magnetization in a 150-nm-thick Cu₂OSeO₃ single crystal at $\text{T}\approx 7$ K. $2.5\times 2.5$ μm² portion of the direct-space images (A–E) from the same region at all fields and the reciprocal-space patterns (F–J) obtained from the corresponding $7.3\times 7.3$ μm² real-space image. The FTs are displayed up to $s=12\times {10}^{-3}{\text{Å}}^{-1}$ for clarity. At B = 95 G and B = 128 G, the helical phase with two different helical domains is observed. B = 160 G represents a transition region from the helical to skyrmion phase. At higher fields, a complete skyrmion phase is observed.

In Cu₂OSeO₃, the helimagnetic phase develops spontaneously upon cooling below 57 K (16, 20) and is visible in Fresnel LTEM as periodically spaced stripes perpendicular to the helices’ screw axis. At the lowest fields of $B=95$ gauss (G) (objective lens off; measured residual magnetic field) and $B=128$ G, we observe two different helimagnetic domains with helices pointing in different directions (Fig. 1 A and B). These two domains are marked by A and B in Fig. 1 A and B, Insets and are characterized by a stripe period of $\approx$ 70 nm. Each domain generates a centrosymmetric pair of peaks in reciprocal space, with the propagation vectors for each helical domain rotated with respect to one another by $48°$ for both $B=95$ G and B = 128 G (Fig. 1 F and G). The intensity of each pair of centrosymmetric peaks in the FT reflects the degree of occupancy of the corresponding helical domain in the real-space image. These results contrast with those of a previous study where only one helimagnetic domain was observed within a probed area of 300 nm (9). However, periodicity values ranging from 50 nm to 70 nm are reported in the literature (9, 16, 28).

At an external field of $B=160$ G, just before the onset of the skyrmion phase, the system is characterized by a glassy distribution with patches of isolated skyrmions and skyrmions in small hexagonal crystallites (Fig.1C and Inset). Here, one of the two helimagnetic domains disappears, and only one orientation for the helices is found. Accordingly, the corresponding FT shows only one set of centrosymmetric peaks (Fig. 1H).

At larger magnetic field strengths, a complete skyrmion lattice forms (Fig. 1 D and E and Insets). The corresponding reciprocal-space image shows the familiar hexagonal pattern (Fig. 1 I and J).

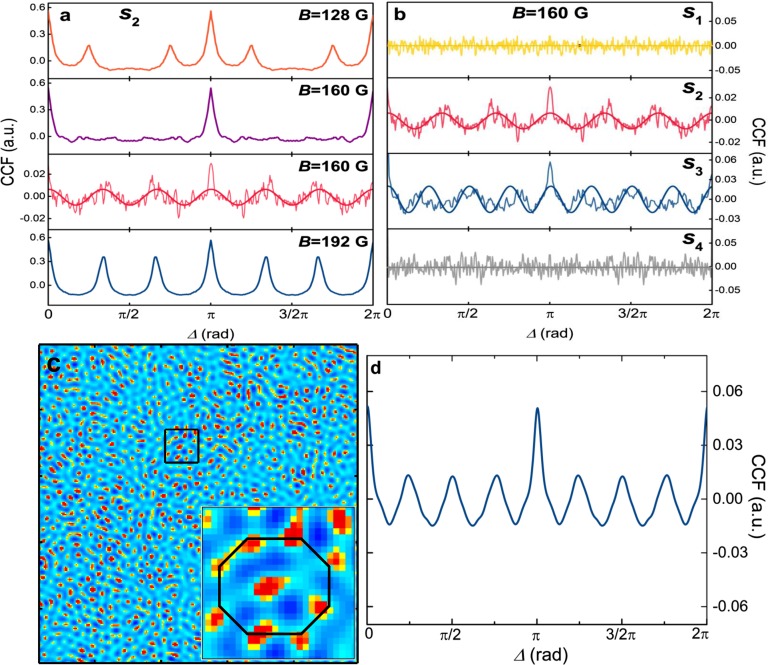
Cross-Correlation Analysis.

To investigate the topology of the magnetic structures at all fields, we analyzed the reciprocal-space patterns obtained from the FT of the direct-space images (shown in Fig. 1 F–J) by means of the cross-correlation function (CCF) defined as

$$C_s\left(\mathrm{\Delta }\right)=\frac{{\langle I\left(s,\theta \right)I\left(s,\theta +\mathrm{\Delta }\right)\rangle }_{\theta }-{\langle I\left(s,\theta \right)\rangle }_{\theta }^2}{{\langle I\left(s,\theta \right)\rangle }_{\theta }^2}$$ [1]

where, $I\left(s,\theta \right)$ represents the scattered intensity at defined scattering vector s, and azimuthal angle θ, and $\mathrm{\Delta }$ is the shift between two azimuthal angles. The angle brackets denote averaging over the variable θ (24, 26, 29–31).

Fig. 1I displays schematically how the computation of the CCF is carried out at a selected scattering vector $s_2$. Such a method has been successfully used to obtain information on the ordering properties of dilute amorphous systems (24) and dense aggregates (25). In the presence of a glassy distribution of skyrmions, the CCF allows the retrieval of information on the local symmetries of the spatial frequency distributions in the sample. We apply this methodology to the FT at the phase transition field, where a glassy distribution of skyrmions is observed. In Fig. 1 G–I, the reciprocal-space scattering distribution is shown for three different applied magnetic fields, and a few significant scattering vectors $s_i$ (with i = 1, 2, 3, 4) are highlighted by white circles. At $B=128$ G, the scattering features related to the helices, which have a pitch of $d_2=70$ nm, are found at $s_2=2\pi /d_2=8.97\times {10}^{-3}{\text{Å}}^{-1}$. At this scattering vector, the computation of the CCF yields the orange trace in Fig. 2A. Upon increasing the magnetic field until the value $B=160$ G, two different periodicities are determined in the CCF at $s_2$. The first, represented by the purple curve, is obtained from the two centrosymmetric peaks originating from the helical distribution at this field. When the peaks from the helical arrangement are masked from the diffraction pattern, the underlying diffuse magnetic scattering in the background at $s_2$ is accessible. The CCF of the background at $s_2$ shows a hexagonal arrangement (red curves) that can be fitted to a harmonic function. The sixfold periodicity retrieved at $B=160$ G from the magnetic speckle in the background reflects the presence of a disordered hexagonal lattice of skyrmions forming in the proximity of the phase transition and coexisting with one of the two helical domains. Thus, at this field, the CCF unravels an incipient orientational order of the skyrmion distribution. Upon entering the skyrmion phase, $B=192$ G, the orientational order is established, and the CCF shows sharp peaks (blue trace). Because all of the periodicities reported in Fig. 2A are found at the same distance in reciprocal space, this confirms the equivalent periodicity of both the helical and skyrmion lattice magnetic structures.

Fig. 2.

Cross-correlation analysis. (A) Field dependence of the CCF at the scattering vector $s_2$ (see Cross-Correlation Analysis for details). (B) Positional ordering of the magnetic speckle at $B=160$ G for four different scattering vectors. At the scattering vectors $s_2$ and $s_3$, respectively, a sixfold and an eightfold modulation are observed. (C) Real-space image at $B=160$ G highlighting a region with octagonal symmetry. (D) Average CCF of the FT of all of the octagonal regions found in the $7.3\times 7.3$ μm² real-space image at $B=160$ G.

The positional order of the incipient skyrmion phase at the transition field ($B=160$ G) can be investigated by looking at the scattering vector dependence of the CCF (Fig. 2B). At $s_1$ ($d_1=64$ nm), no periodicities are determined (yellow trace), and at $s_2$ and $s_3$, corresponding to a real-space distance of $d_2=70$ nm and $d_3=71$ nm, sixfold (red trace) and eightfold (blue trace) modulated CCFs, respectively, are found. The eightfold symmetry is found at a scattering vector corresponding to a slightly larger lattice constant, as expected from packing a larger number of skyrmions within the unit cell. At scattering vectors smaller than $s_4$ ($d_4=85$ nm), no periodicities are determined. This observation suggests that patches of both orientationally disordered hexagonal and octagonal distributions of skyrmions are found, in which the skyrmion–skyrmion distance is included in the range $70\pm 1$ nm. The presence of such an octagonal distribution can also be seen directly in the real-space image as highlighted in Fig. 2C. The average CCF computed from the FT of all of the octagonal regions found in the $7.3\times 7.3$ μm² real-space image is shown in Fig. 2D, indicating a clear eightfold periodicity.

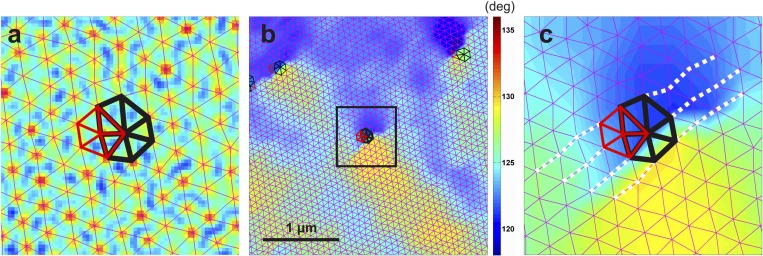
Formation of Skyrmion Domains.

In the skyrmion phase, we evaluate the role of disorder and defects in the lattice by locating the skyrmions in the real-space image and counting the number of nearest neighbors of each skyrmion via the Delaunay triangulation. A representative skyrmion lattice at $B=483$ G is shown in Fig. 3A in the background, and the Delaunay triangulated lattice is shown as magenta lines. A perfect skyrmion coordination has a hexagonal symmetry. An imperfect skyrmion coordination can have more or less than six neighbors and forms a lattice defect. A skyrmion pair with seven and five neighbors is highlighted with black and red lines, respectively. A spatial angle map of the orientation of skyrmions (SI Appendix, Skyrmion Positions and Angle Map Construction) is depicted in Fig. 3B. The formation of a multidomain skyrmion lattice is readily visible in this map, with different colors representing different domains. The Delaunay triangulation and the defects are plotted on the foreground of this map. It is important to note that the domain boundaries coincide with the defects. A zoom-in of a small region marked by a square in Fig. 3B is shown in Fig. 3C. The formation of a dislocation at the site of a five–seven defect is evidenced, as four lines can be drawn on one side of the seven–five defect, whereas only three lines can be drawn on the other side. This dislocation line forms the domain boundary between the two orientations of the skyrmion lattice that are characterized by blue and yellow regions. A similar behavior has been observed at all of the magnetic fields, and the images are shown in SI Appendix, Figs. S9–S12. However, as the magnetic field is increased, the dislocation density decreases, and large single-domain regions form. This highlights the fact that a stronger applied field induces higher levels of order.

Fig. 3.

Formation of the skyrmion domains. (A) Real skyrmion lattice and a Delaunay triangulated lattice (magenta lines) obtained for $B=483$ G. A skyrmion pair with seven and five neighbors, which forms a lattice defect, is highlighted with black and red lines, respectively. (B) Spatial angle map of the skyrmion lattice plotted together with the Delaunay triangulation and defects. (C) A zoom-in of the region marked by the square in B. The presence of a dislocation line at the domain boundary is evidenced.

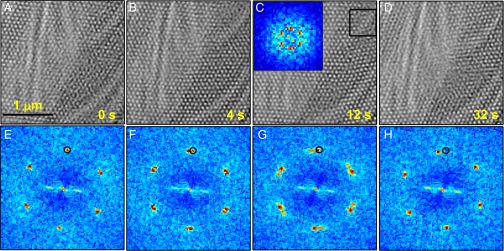
Fluctuation of Skyrmion Domains.

To understand the fluctuations of the skyrmion lattice in real time, we analyzed a movie acquired for 50 s. Each frame is exposed for 100 ms, and an image is acquired every 500 ms. The full movie is shown in Movie S1, and four frames at selected time points are displayed in Fig. 4. Fig. 4 A–D depicts the real-space images, and Fig. 4 E–H represents the corresponding FTs. Within this movie, the orientation of the skyrmion lattice is observed to fluctuate, and regions of well-distinguished orientations can be separated. At 0 s (Fig. 4 A and E), the skyrmion lattice forms a single domain. The corresponding FT shows a relatively sharp hexagonal pattern. The position of a single Bragg peak marked by a black circle can be used as the reference position for marking the deviations in the subsequent frames. At 4 s (Fig. 4 B and F), two domains with slightly different orientations are formed. Accordingly, a set of split Bragg peaks is obtained in the reciprocal-space map, where the splitting corresponds to the angle between the two domains in the sample with different skyrmion lattice orientations. One of the two subpeaks is found within the black reference circle, indicating that, out of the two domains, one domain has the same orientation as that found at 0 s and a second domain with a slightly different orientation has formed within this acquisition time. At 12 s (Fig. 4 C and G), the peak separation is larger and the subpeaks are farther away from the black circle, indicating a stronger fluctuation of the skyrmion lattice. An interesting point to note in this time frame is that the reciprocal-space map of a small region marked by the square in Fig. 4C also reveals the tendency to have split Bragg peaks (Fig. 4C, Inset). In this particular time and space point, either the two different orientations are found in the same frame at the same time or switching between the two has happened within the 100-ms exposure time. At 32 s (Fig. 4 D and H), one of the two domains disappears and forms a new single-domain skyrmion lattice that is rotated by about $11°$ from the domain formed at 0 s. This is evidenced by the single Bragg peak found away from the black circle in the FT. Our results clearly emphasize the importance of the time dimension for a proper investigation of the system. Moreover, these observations underline the importance of resolving the skrymion lattice in space and time for revealing its exact topology and the dynamical evolution caused by fluctuations and disordering effects.

Fig. 4.

Four different frames of Movie S1 are displayed. (A–D) The real-space images and (E–H) the corresponding FTs: (A and E) 0 s, (B and F) 4 s, (C and G) 12 s, and (D and H) 32 s. Fluctuations of the skyrmion lattice and formation of domains with different orientations as a function of time are evidenced by the splitting and unsplitting of the Bragg peaks and their continuous change of position.

Discussion

In our nanoslice, the observation of a splitting in the magnetic Bragg diffraction is caused by the spatial and/or temporal overlap of different disorder-induced lattice orientations within the experimental acquisition time. However, it is important to point out that the way in which disorder affects the skyrmion lattice orientation in a nanoslice can differ significantly from a bulk crystal, such as the one investigated in ref. 16, changing the details of the dynamical evolution and the spatial topology of the misoriented grains. This could explain the difference in the size of the mesoscopic domains and in their evolution upon applied magnetic field. Remarkably, in specific areas of the sample, we find that disorder can provoke sudden switches between well-defined orientations. This suggests that the energy landscape of the magnetic system has a complex nature, with several local minima separated by subtle barriers.

The ability to resolve the switching between these different minima would allow estimation and control of the energy barriers via ad hoc external stimuli such as light, electrons, or electric fields. Currently, the switching we observed was not entirely resolved due to limitations in the time resolution of the camera-rate acquisitions. Future experiments with time resolution in the microseconds to nanoseconds in our ultrafast TEM (32, 33) should therefore be able to fully resolve this behavior. The development of methods for the study of the symmetry and dynamics of large 2D arrays of skyrmions is an essential step toward their possible application in spintronic devices. Recent results have demonstrated the possibility of manipulating skyrmions at room temperature, making these magnetic structures more appealing for realistic applications (11, 34).

Materials and Methods

High-quality single crystals of Cu₂OSeO₃ were synthesized by the method of chemical vapor transport redox reactions. After mechanical thinning to about 30 μm, the sample was thinned to 150 nm by FIB using the classical H-bar technique. A fiducial layer of Pt was deposited to prevent preparation artifacts like curtaining. A final cleaning with 5-kV and 2-kV ion beam was applied to remove the amorphized layer and to minimize Ga implantation. The magnetic structures of the samples were investigated by using JEOL JEM-2200FS cryo-LTEM. Images were acquired in the Fresnel mode, i.e., defocused imaging (35), so that the objective lens was not used for imaging but for applying the magnetic field. The microscope was operated at 200 kV and equipped with a field emission source. The sample was cooled down to $7-10$ K using the liquid helium TEM holder (Gatan ULTS), and a magnetic field ranging from 95 G to 483 G was applied normal to the thin plate along the [111] direction. The magnetic field that is parallel to the electron optic axis was directly measured and calibrated at the specimen position.