Biomechanical properties of ileum after systemic treatment with epithelial growth factor

Abstract

AIM: Systemic treatment with epidermal growth factor (EGF) leads to growth of all parts of the small intestine in normal functioning rats. In this study, we investigated the effect of this growth process on morphometric and biomechanical parameters of ileum.

METHODS: Rats were treated with EGF (150 μg·kg^-1d^-1) or placebo via osmotic minipumps for 2, 4, 7, and 14 d. A segment of ileum was removed. The morphology at no-load state and zero-stress state was measured and passive biomechanical properties were assessed using a biaxial test machine (combined inflation and axial stretching).

RESULTS: The ileum weight increased after EGF administration. After 4 d’ EGF treatment, the wall thickness was increased. Significantly smaller inner perimeters were seen in 4 d and 7 d EGF treatment groups. The opening angle and residual strain began to increase after 7 d’ EGF treatment. Wall stiffness, evaluated from the stress-strain curves, showed a continuous decrease in circumferential direction during the first 7 d’ EGF treatment. The longitudinal stiffness increased during the first 7 d. The stress-strain curves for both circumferential and longitudinal direction tended to shift back to normal 14 d after starting EGF administration.

CONCLUSION: EGF can cause significant changes both in the morphology and in the passive mechanical properties of the rat ileum.

INTRODUCTION

Epidermal growth factor (EGF) is a peptide growth factor belonging to the EGF family[1]. Throughout the last decade, the pharmacological potential of systemic treatment of EGF has been explored[2]. In the gastrointestinal tract, EGF causes growth, inhibits gastric acid secretion, and leads to changes in electric potentials, enzyme activity and transport of amino acids[3-6]. Due to the pronounced effects on intestinal mucosa, the therapeutic potential of systemic treatment of EGF has been explored in animal experiments. For example it has been shown that EGF accelerates adaptive growth of the small intestine in different species[7-10].

Only few studies have addressed the effect of systemic treatment of EGF on the normal small intestine. In a series of studies, we have examined its effect on the morphological and biomechanical properties of the small intestine. Vinter-Jensen, et al[11] used impedance planimetry to examine the tension-strain properties of the intestinal wall after EGF treatment and found that the circumferential wall stiffness decreased during EGF treatment. However, their study had limitations because the circumferential strain was referenced to the no-load state rather than to the zero-stress state and the mechanical properties were only studied for the circumferential direction.

The present study was to investigate the time-dependent effect of systemic treatment with EGF on the passive biomechanical properties of the small intestine. Segments obtained from the ileum were tested in a biaxial mechanical test machine that renders possible simultaneous inflation and longitudinal stretch. Stress and strain were computed and material constants were derived for the circumferential and longitudinal directions.

MATERIALS AND METHODS

Animals and study design

Thirty-four female Wistar rats (bred at the Department of Pathology, Aalborg Hospital Denmark) weighing 190-200 g were included in this study. The animals were housed individually in cages on white special span wall bedding (temperature 21 °C, humidity 55% ± 5%, dark/light cycle 12-h shift). They were fed on a standard laboratory diet. The study complied with Danish regulations for care and use of laboratory animals.

Twenty-two rats were allocated to four groups and treated for 2 (n = 6), 4 (n = 6), 7 (n = 6), and 14 (n = 4) d with human recombinant EGF (150 μg/kg/d, Upstate Biotechnology, New York, USA) using osmotic minipumps (ALZET 2001; ALZA, Palo Alto, California, USA). Twelve rats served as controls (n = 3 for each time period). The body weights of both the control and EGF treated rats were measured at the beginning and the end of the study.

Collection of specimens

After treatment, the rats were anaesthetized (pentobarbital 50 mg·kg^-1 intraperitoneally) and a midline laparotomy was performed. The calcium antagonist papaverine (60 mg·kg^-1) was injected into the lower thoracic aorta through a cannula (22 G/25 mm) in order to abolish any contractile activity in the gastrointestinal tract. A 5.5-cm-long segment from ileum was excised after the attainment of muscle relaxation (no visible contraction was observed). The residual contents in the lumen were gently cleared using saline and the in vitro weight and length of the segment were measured. Then the segment was placed in cold Krebs solution containing 6% dextran aerated with a gas mixture (95% O₂ and 5% CO₂, pH7.4). Rings of 1-2 mm in length were cut at the edge of the tissue for no-load and zero-stress state measurements. The remaining part was used for the biaxial test.

Stress-strain experiment

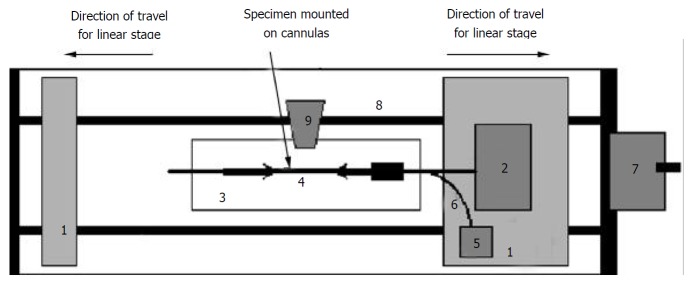
The stress-strain test was conducted on the self-developed biaxial machine (Figure 1), which consists of the force and pressure transducers, the organ bath, motion stage and electronics. The specimen was bathed in the physiological Krebs solution. The two ends of the sample were tied with silk threads on the cannulas and the length between the threads was measured. The length in vitro was approximately 30 mm. Then the cannulas were mounted on the rods. The rod on the right side contained a T-connector for changing the pressure in the ileum. The rod on the right was also attached to a force transducer. The rods could be moved towards or apart from each other at controlled rates by two linear stages using a motor. The whole segment was photographed using a video camera (SONY CCD Camera, Japan) for later analysis of length and diameter.

Figure 1.

Legend, biaxial test machine setup. 1: Stage, 2: Force transducer, 3: Organ bath, 4: Specimen, 5: Pressure transducer, 6: Infusion channel, 7: Motor for linear stage, 8: Rails for linear stage, 9: Video camera.

In mechanical testing of living tissues, preconditioning was necessary to obtain repeatable results. This meant that after the specimen was installed in the test machine, the loading and unloading processes were repeated for a number of cycles until the stress-strain relationship became stabilized. The number of cycles required depended on the tissue and method of preparation. In these experiments, we preconditioned the ileum at 6 cmH₂O pressure, 4 stretch cycles to stretch ratio 1.25. The segment was then elongated to stretch ratios of 1.0, 1.08, 1.16, and 1.25. At each stretch level, we applied the pressure to the levels of 0, 2, 4, and 6 cmH₂O. The corresponding diameter and gauge length, displacement and axial force at each stress level were monitored.

Determination of no-load state and zero-stress state

The tissue rings were immersed separately in small organ baths containing the aerated Krebs solution. They were photographed in the no-load state and then cut radially on the anti-mesenteric side to obtain their zero-stress state (Figure 2). A 30-min-period was allowed for equilibration after the radial cut and the specimens were photographed again. The selection of this time period was based on pilot experiments.

Figure 2.

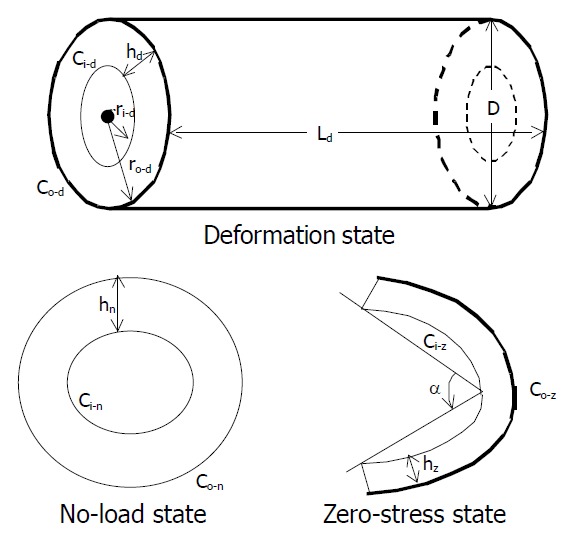
Legend, illustrations of intestinal small intestinal seg-ment in the no-load, zero-stress and deformed states. C, h, α, denoted the circumference, thickness, and opening angle, respectively. The subscripts n, z, d denoted the no-load state, zero stress state and deformed state, respectively. The sub-scripts i, o referred to the inner (mucosal) surface, outer (serosal) surface, respectively.

Data analysis

Morphometric data were obtained from the digitalized images of the segments in the zero-stress, no-load and deformed states. The measurements were done using dedicated software (Sigmascan 4.0, Jandel Scientific, USA). The following data were measured from each specimen at the no-load and zero-stress states (illustrated in Figure 2), which were the circumferential length (C), the wall thickness (h), the wall area (A), and the opening angle at the zero-stress state (α). The subscripts i, o, m, n, z and d refered to the inner (mucosal) surface, outer (serosal) surface, the mid-wall, the no-load state, zero-stress state and deformed condition, respectively. The opening angle α was defined as the angle subtended by two radii drawn from the midpoint of the inner wall to the inner tips of two ends of the specimen. Furthermore, the outer diameter (D) and the length (L_d) were measured from the images of the deformed segments.

The measured data were used for computation of the biomechanical parameters. Circumferential residual Green’s strain at the mucosal and serosal surface: E_i = 1/2[(C_i-n/C_i-z)²-1] and E_o = 1/2[(C_o-n/C_o-z)²-1] (1).

The stress and strain of the intestine in the deformed state were determined under assumptions that the intestinal wall was thin and homogenous and the intestinal geometry was a circular tube when pressurized. The circularity assumption had been verified in yet unpublished studies. The simplification we wished to make under the thin wall assumption was that the normal stress in the radial direction, σ_rr, was negligible and that the stresses σ_θθ, and σ_ϕϕ were approximately uniform throughout the wall thickness. Here r, θ, ϕ were polar coordinates in radial, circumferential and axial directions, respectively. The calculations were based on knowing the zero-state, no-load state dimensions, the outer diameters and lengths of the specimen at varying pressures, and assuming incompressibility of the intestinal wall. The longitudinal mid-wall stretch ratio, λ_ϕϕ = L_d/L_n; the luminal radius, Math 1; the wall thickness, h_d = r_o-d-r_i-d; the mucosal circumferential length, C_i-d = 2πr_i-d; the serosal circumferential length, C_o-d = 2πr_o-d; the mid-wall circumferential length,C_m-d = 1/2 (C_i-d + C_o-d); the mid-wall circumferential length at zero-stress state C_m-z = 1/2 (C_i-z + C_o-z), the circumferential stretch ratio, λ_ϕϕ = C_m-d/C_m-z. The longitudinal mid-wall stretch ratio was referenced to the no-load state because tissue strips were not cut for obtaining the zero-stress state in both directions. However, the longitudinal mid-wall length in rat intestine did not differ between the no-load and zero-stress states.

Math 1

Math 1.

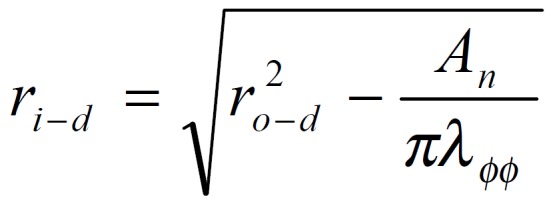
Math(A1).

Kirchhoff’s stress and Green’s strain at a given pressure were computed according to the following equations. The circumferential and longitudinal Kirchhoff’s stress: Math 2 (2)

Math 2

Math 2.

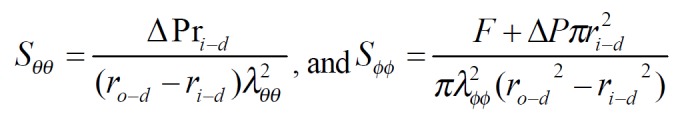
Math(A1).

Where △P was the transmural pressure difference, F was the force applied on the two ends of intestine. The circumferential and longitudinal midwall Green’s strain: Math 3 (3)

Math 3

Math 3.

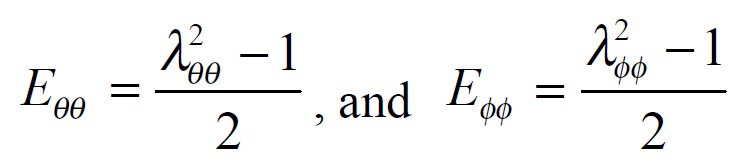
Math(A1).

The stress and strain under each level of pressure and stretch ratio were calculated. In order to compare the stress-strain relationships among different EGF groups, one dimensional stress-strain curve was fitted, averaged and plotted: Circumferential stress-strain relationship (P = 0 to P = 6 cmH₂O (λ_ϕϕ = 1)) was fitted by the exponential equation: strain = y₀ + kexp (stress/t). Longitudinal stress-strain relationship (λ_ϕϕ = 1 to λ_ϕϕ = 1.25 (P = 0 cmH₂O)) was fitted by another exponential equation because of different curve shapes, stress = exp (a + b × strain). Where y₀, k, and t, a, b were derived from the curve-fit regression done for each of segments. After fitting and averaging, the average curves with error bar could be obtained in different groups.

The exponential strain expression proposed by Fung[12] was applied to a set of test results on EGF treatment ileum. The stress and strain at a fixed stretch ratio of λ_ϕϕ = 1.16 and at varying pressure (P = 0, 2, 4, 6 cmH₂O) were calculated and fitted to the function. Math 4 (4) where W was the strain energy per unit mass of the tissue, and ρ₀ was the mass density (mass per unit volume) in the initial zero-stress state. Then ρ₀W⁽²⁾ was the strain energy per unit volume of the tissue at zero-stress state for two dimensions. From Math 5 (5) We obtained Math 6 (6) Where Math 7 (7) Where C (with units of stress,) and a₁, a₂, a₄ (dimensionless) were material constants, E_θθ^*, E_ϕϕ^* were strains corresponding to a selected pair of stresses S_θθ^*, S_ϕϕ^*. The material constants were determined by a modified version of Marquardt’s nonlinear least-squares algorithm.

Math 4

Math 4.

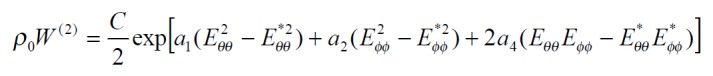
Math(A1).

Math 5

Math 5.

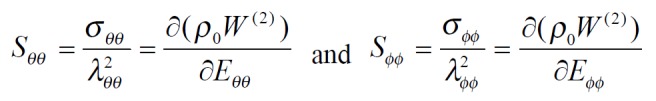
Math(A1).

Math 6

Math 6.

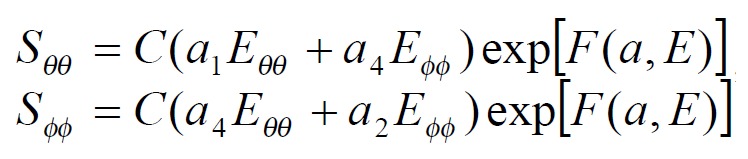
Math(A1).

Math 7

Math 7.

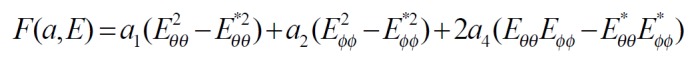
Math(A1).

The meaning of the material constants was discussed in detail by Fung[12]. Constant a₁ would affect the curve for S_θθ vs. E_θθ, the higher the a₁, the curve of S_θθ vs. E_θθ would leave the origin closer to the strain axis, and rise more rapidly, the more non-linear the curve was. Constant a₂ would affect the curve for S_ϕϕ vs. E_ϕϕ in a similar way. Constant a₄ specified the cross talk between the circumferential and longitudinal directions. The constant C fixed the scale on the stress axis. The larger the value of a₁, a₂ and a₄ was, the smaller C was[12].

Statistical analysis

Data were expressed as mean ± SEM. One-way analysis of variance was used to detect variations between treatment groups (Sigmastat 2.0^TM, Jandel Scientific, Germany). In case of significance (P < 0.05), differences were tested between the control group and EGF-treated groups at 2, 4, 7, and 14 d treatment (Dunnet’s Test). If the normality test failed, Kruskal-Wallis one way analysis of variance on ranks was used instead.

RESULTS

Weight and morphological data

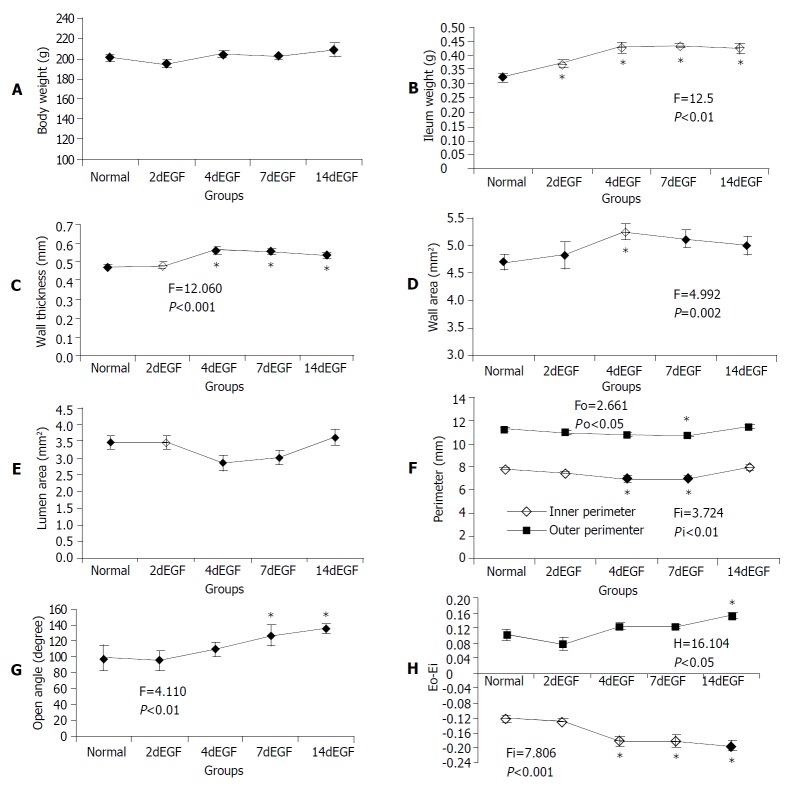
The total body weight did not change (Figure 3A). The ileum weight began to increase after 2 d’ EGF treatment (Figure 3B). The wall thickness increased significantly after 4 d’ EGF treatment, it did not change further (Figure 3C). A significantly larger wall area was observed in the 4 d’ treatment group (Figure 3D). The luminal area did not change significantly (Figure 3E). However, a significantly smaller inner perimeter was observed in the 4 d, and 7 d’ EGF treatment groups, but not in the 14 d’ group (Figure 3F).

Figure 3.

Legend, morphometric data of ileum in the no-load (A-F) and zero-stress states (G-H). F and P values were from one-way ANOVA for different treatment groups: If significant difference (P < 0.05) was found using one-way ANOVA (marked with a), multiple comparisons with normal controls were done using Dunnet’s test. Significantly different groups were marked with b.

Zero-stress state data

The opening angle increased significantly after 7 d’ EGF treatment and continued to increase up to 14 d (Figure 3G). The mucosal residual strain was compressive in all groups and decreased from 4 d of EGF treatment. The serosal residual strain was tensile with relatively higher values after 14 d of EGF treatment (Figure 3H).

Biomechanical data

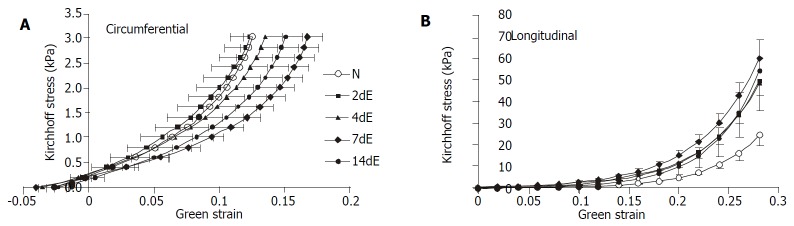
The stress-strain relationships are shown in Figure 4. In circumferential direction, the curves representing 4 d and 7 d of EGF treatment were shifted to the right, whereas 14 d’ EGF treatment curve shifted back towards normal. In longitudinal direction, the stress-strain curves representing 4 d and 7 d of EGF treatment were shifted to the left. Like the circumferential direction, the curves shifted towards normal after 14 d’ EGF treatment.

Figure 4.

Legend, intestinal stress-strain curves in the EGF-treated and normal control groups. Translation of the stress-strain curve to the right in the coordinate system implied tissue softening (decreased stiffness) and vice versa.

The derived material constants a₁, a₂, a₄, and C from the strain energy function are illustrated in Table 1. Constant a₁ and a₂ having comparably smaller SEM values were therefore more stable than the other parameters. A significantly smaller a₁ value was found in the 7 d’ and 14 d’ EGF treatment groups and larger a₂ values were found in the 2 d’ and 7 d’ EGF treatment groups. This demonstrated that 7 d’ EGF treatment had the lowest circumferential stiffness and comparatively high longitudinal stiffness, and that the remodeling was most significant in the 7 d’ EGF treatment group.

Table 1.

Material constants

	Normal	2dEGF	4dEGF	7dEGF	14dEGF
a1a	25.42 ± 1.91	18.19 ± 2.80	19.32 ± 3.91	11.57 ± 2.04b	13.61 ± 3.00b
a2a	21.51 ± 3.19	36.24 ± 0.95b	24.90 ± 3.72	34.74 ± 5.17b	27.51 ± 4.41
a4	6.41 ± 1.20	12.20 ± 2.98	7.13 ± 3.53	5.39 ± 1.29	4.78 ± 1.15
C (kPa)	1.13 ± 0.18	1.30 ± 0.27	2.32 ± 0.97	1.75 ± 0.30	1.02 ± 0.12

A: One-way ANOVA result: P < 0.05; B: Post analysis (Dunnet´s test) result: significantly different from normal control group (P < 0.05).

DISCUSSION

The major findings in the present study were that EGF treatment induced time-dependent morphometric and biomechanical remodeling in the ileum. The ileum weight and wall thickness increased. The biomechanical changes were characterized by increased opening angle, inner and outer residual strains, decreased circumferential wall stiffness and increased longitudinal wall stiffness.

As the function of the GI tract is to a large degree mechanical, it has become increasingly popular to acquire biomechanical information on the GI tract[13-17]. However, many aspects of its biomechanical function are still largely left unexplored. Previous investigations were mainly conducted on uni-axial isolated strip experiments and balloon distension[18,19]. In the isolated strip studies, the structural integrity of the organ wall was not preserved and the strip was not necessarily in its zero-stress state at resting conditions since large residual strains existed in the GI tract[19]. In the balloon distension test, by means of impedance planimetry, the luminal cross-sectional area (CSA) could be measured. CSA as function of pressure provided important information on luminal dimensions during the loading but gave little information about material properties without further mechanical analysis. Furthermore, the tension-strain relationship was only computed for the circumferential direction and the strain was not referenced to the zero stress state[18].

The zero stress state of an organ is the state at which the organ is stress-free, meaning that all external and internal forces are removed. Vaishnav and Vossoughi[20] and Fung[21] independently reported respectively that the no-load state of a blood vessel was not the zero stress state. Recently, residual strains were demonstrated in the esophagus, small intestine, and large intestine[14-16,22-28] and were found to be closely related to the growth and remodeling[24-30]. Hence the analysis of stress and strain begins with identification of the zero stress state.

This study was to explore how EGF affects geometric and biomechanical remodeling. EGF induced remodeling of the material structure, zero-stress state, and mechanical properties. The changes were quantified in terms of material constants in the constitutive equation. For computation of mechanical parameters we used video image techniques during loading and at no-load and zero-stress states. Assuming the intestine wall to be a membrane, biaxial experiments were done and a two- dimensional pseudostrain energy function was used to express the stress-strain relationship with reference to the zero-stress state. The use of pseudoelasticity to describe biological materials has been justified by Fung et al[12]. The vascular study by Liu and Fung[31] found that the zero stress state and the material constants changed with the development of diabetes.

Remodeling of the small intestine was evident after 4 d’ EGF treatment with increased wall thickness and decreased luminal area. This was consistent with Vinter-Jensen’s study[11]. They demonstrated that EGF stimulated intestinal wall thickness growth before the surface area growth. According to the histology observation, the growth progress mainly involved the mucosa layer. The speed of growth began to decrease after 4 d’ EGF treatment.

The small intestinal residual strains were negative at the mucosal layer and positive at the serosal layer. This implied that the mucosa was under compression in the no-load state and at physiological conditions in the low pressure range, whereas the muscle layers were in tension. As expected, both the residual strain and the opening angle increased in a time-dependent manner. The change of the opening angle was a result of non-uniform tissue remodeling of the organ wall. The opening angle increases when the inner layers had a higher growth rate than the outer layers or when the outer layer’ atrophy was more severe than the inner layer[32]. In the present EGF study, the mucosa growth was much faster than that in the other layers, which resulted in the increased opening angle and residual strains. It has been demonstrated that residual stress reduces the stress concentration at the inner wall of the GI tract at no-load and homeostatic states[15,16,22]. The residual stress in the resting condition may also serve as a growth-regulation factor[33]. However, additional studies are needed to investigate whether the growth influences the residual stress distribution or vice versa.

The biaxial test showed that the wall stiffness changed in response to EGF treatment. After 7 d’ EGF treatment, the wall stiffness decreased in circumferential direction and increased in longitudinal direction. The wall stiffness remodeled towards the normal state in both directions after 14 d’ EGF treatment. In circumferential direction, the result was consistent with Vinter-Jensen’s report[11]. The different tendency of intestinal wall stiffness change in the two directions demonstrated that EGF-induced tissue remodeling was heterogeneous in the ileum. The elastic modulus of the intestine wall was closely related to the morphological wall composition and the stiffness was mainly dependent on the collagen in the submucosal layer[15,34]. The submucosal layer did not remodel to the same degree as the mucosal layer. Therefore, the intestinal wall became softer in the circumferential direction after EGF treatment. At this point we could not explain the different remodeling in the two directions. A possible explanation is that the collagen orientation changed its direction during EGF treatment. This study did not intend to evaluate the collagen orientation angle, so this needs to be evaluated in future studies. Another noticeable result was that after 14 d’ EGF treatment the curves shifted towards normal in both directions. We hypothesize that the pronounced proliferation of the intestine in the first week is due to direct stimulation by exogenous EGF. However, after one week, a negative feedback mechanism of the organ reduced the response to endogeneous EGF, resulting in reduced growth speed of the intestine. Finally, after two weeks, the remodeling might be determined by the stress in the tissue in accordance with the stress-growth law proposed by Fung[21].

ACKNOWLEDGEMENT

The recombinant EGF was a generous gift from Professor Esam Z. Dajani, International Drug Development Consultants Corporation, a Division of Mid Gulf U.S.A., Inc., Long Grove, Illinois, U.S.A.