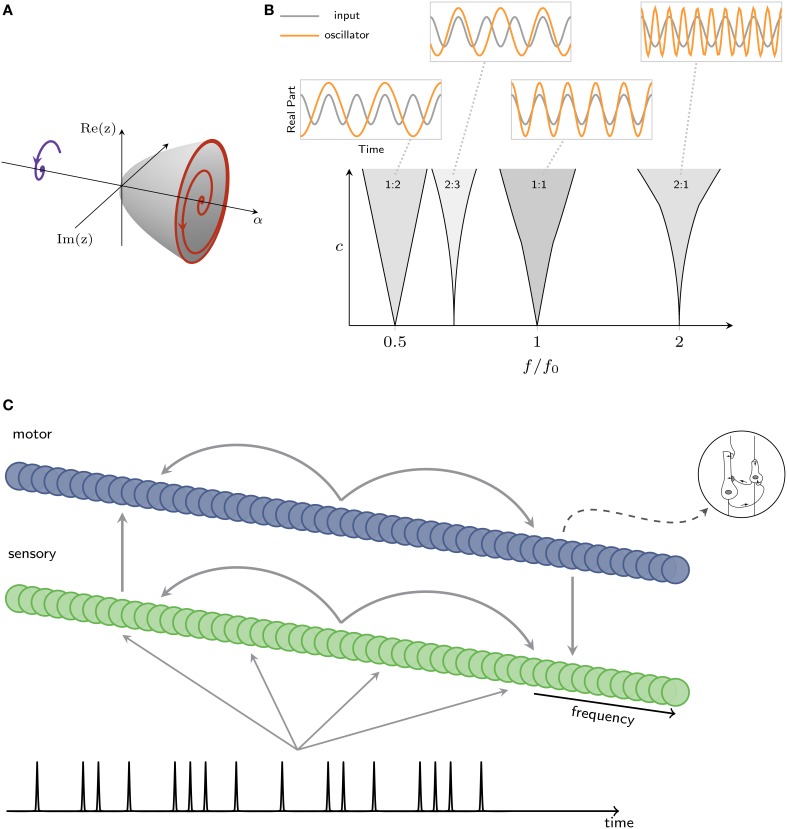
Figure 4.

(A) Intrinsic oscillatory dynamics can take the form of a Hopf bifurcation, where a value α = 0 is the critical point, between damped (left) and spontaneous (right) oscillation. (B) Mode locking in the canonical model. Within each resonance region (shaded), the canonical model mode-locks to input at the ratio shown in figure (c: coupling strength, f: oscillator's intrinsic frequency, f₀: input frequency). Insets show the inputs and traces produced by a canonical model. (C) Architecture of a model that captures interacting oscillatory dynamics in sensory and motor networks. A rhythm is input to a sensory network; sensory and motor networks are reciprocally connected, providing input to one another.