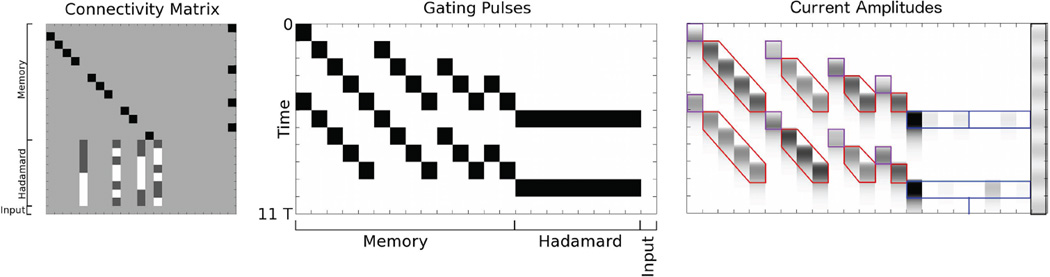
FIG. 5.

4 × 4 Hadamard transform on a window of input values moving in time. (Left) Connectivity Matrix. White denotes −1/2, light gray denotes 0, dark gray denotes 1/2, and black denotes 1. The connectivity matrix is subdivided into three sets of rows. “Memory” designates Read In and (non-cyclic) Memory populations. “Hadamard” designates populations for the calculation of Hadamard coefficients. Because the packet amplitudes can only be positive, the Hadamard transform is divided into two parallel operations, one that results in positive coefficients and one that results in absolute values of negative coefficients. “Input” designates filtered input from an outside source. (Middle) Gating Pulses. White denotes 0, black denotes g₀. T/τ = 2. Time runs from top to bottom. We show the computation for two successive windows, each of length 4T. The pulses transduce the input into four memory chains of length 4T, 3T, 2T and T. Thus, four temporally sequential inputs are bound in four of the memory populations beginning at times t = 4, 8T. Hadamard transforms are performed beginning at t = 5, 9T. Note that the second read in starts one packet length before the Hadamard transform so that the temporal windows are adjacent. (Right) Current Amplitudes. White denotes 0, black denotes the maximum current amplitude. Purple outlines denote Read In, red denote Memory and blue denote Hadamard transform populations. The left four Hadamard outputs are positive coefficients. The right four are absolute values of negative coefficients. The sinusoidal input waveform is shown to the right.