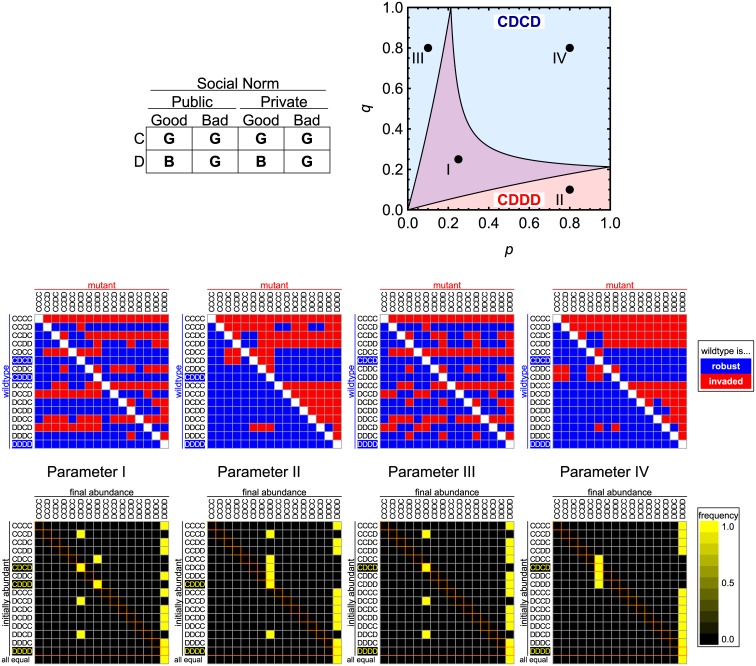
Fig 4. Numerical tests of evolutionary dynamics for a particular social norm which stabilizes both CDCD and CDDD (in addition to DDDD).
Top left: the social norm that is studied. Top right: our theoretical prediction of cooperative ESS for various p and q for b/c = 5. CDCD is ESS in the blue region. CDDD is ESS in the red region. Both are ESS in the purple region. Middle and Bottom rows: results of deterministic computer simulations. The chance of erroneous reputation assignment is set to e = 0.03. Middle row: pairwise comparison between a wildtype (initial frequency = 0.99) and a mutant (= 0.01). Invasion is deemed successful if the mutant’s frequency exceeds 0.01 after a long run. We observe no neutrality. Bottom row: competition among 16 action rules, where one of them is initially abundant (= 0.99) and the others are rare (= 0.01/15 each), or all 16 are initially equally abundant (= 1/16; ‘all equal’ treatment). Our theoretical prediction is in agreement with this numerical analysis. Parameter values (p, q) are I:(0.25, 0.25), II:(0.8, 0.1), III:(0.1, 0.8) and IV:(0.8, 0.8).