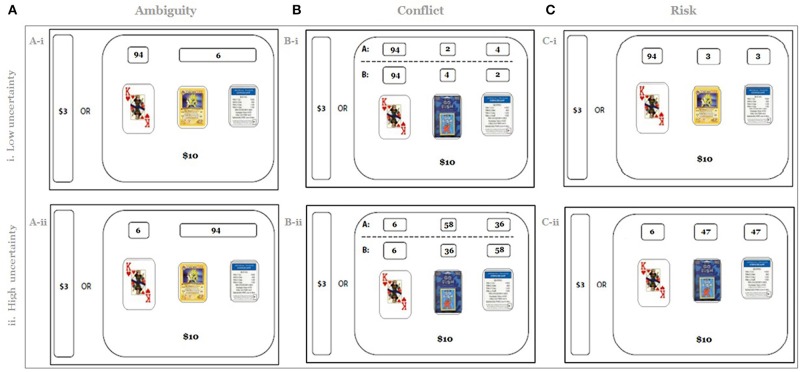
Figure 1.

Experimental design. Participants were asked to play a series of lotteries under several experimental conditions (A: ambiguity, B: conflict, C: risk). For each lottery, they would have to guess the type of card that they would draw from a mixed deck of 100 different cards (e.g., Trivial Pursuit, Pokémon, etc.). On each trial, participants could refuse to gamble, in which case they received $3. If they chose to play the lottery, they would receive $10 for a correct guess or nothing for an incorrect guess. In the ambiguity condition, the total number of “Type 2” and “Type 3” cards was provided (e.g., total of six Pokémon and Monopoly cards, A-i). In the conflict condition, participants received conflicting information about the numbers of Type 2 and Type 3 cards (e.g., two Monopoly cards and four Go-Fish cards vs. four Monopoly cards and two Go-Fish cards, B-i). In the risk condition the number of cards of Type 2 was always equal to the number of cards of Type 3. Note that the ambiguity gambles (A) are matched with the conflict gambles (B) and with risk gambles (C) on both expected value and variance under the assumption of a rational decision maker. The total number of cards in Piles 2 and 3 in this paper is referred to as the level of ambiguity (conflict); 30 unique combinations of cards of Type 1, Type 2, and Type 3 under each type of uncertainty were included in the experiment (see Supplementary Materials S.1); level of ambiguity (conflict) thus varied from 6 (A-i, B-i, the lowest of 30 levels of uncertainty) to 94 (A-ii, B-ii, the highest of 30 levels of uncertainty).