IsoDOT Detects Differential RNA-isoform Expression/Usage with respect to a Categorical or Continuous Covariate with High Sensitivity and Specificity

Abstract

We have developed a statistical method named IsoDOT to assess differential isoform expression (DIE) and differential isoform usage (DIU) using RNA-seq data. Here isoform usage refers to relative isoform expression given the total expression of the corresponding gene. IsoDOT performs two tasks that cannot be accomplished by existing methods: to test DIE/DIU with respect to a continuous covariate, and to test DIE/DIU for one case versus one control. The latter task is not an uncommon situation in practice, e.g., comparing the paternal and maternal alleles of one individual or comparing tumor and normal samples of one cancer patient. Simulation studies demonstrate the high sensitivity and specificity of IsoDOT. We apply IsoDOT to study the effects of haloperidol treatment on the mouse transcriptome and identify a group of genes whose isoform usages respond to haloperidol treatment.

In the genomes of higher eukaryotes, the DNA sequence of a gene often includes multiple exons that are separated by introns. A multi-exon gene may encode several RNA isoforms, each with a unique subset of exons. Recent studies have shown that more than 90% of human genes have multiple RNA isoforms which may be differentially expressed across tissues or developmental stages [Wang et al., 2008, Pan et al., 2008], and about 75% of human genes produce multiple RNA isoforms within a given cell type [Djebali et al., 2012]. Therefore, study of RNA-isoform expression and its regulation is of great importance to understand the functional complexity of a living organism, the evolutionary changes in transcriptome [Barbosa-Morais et al., 2012], and the genomic basis of human diseases [Wang and Cooper, 2007].

Gene expression has traditionally been measured by microarrays or exon arrays, most of which provide just a handful of probes per gene and poor resolution to distinguish multiple isoforms. [Purdom et al., 2008, Richard et al., 2010]. RNA sequencing (RNA-seq), on the other hand, provides much better data for this purpose [Wang et al., 2009]. In RNA-seq, fragments of RNA molecules (typically 200-500 bps long) are reverse transcribed and amplified, followed by sequencing of one or both ends (single vs paired-end). Each sequence is referred to as a read, which could be 30 - 150 bps or even longer. Reads are then mapped to a reference genome and the number of fragments overlapping each gene is counted. The expression of the j-th gene in the i-th sample is measured by a normalized fragment count after adjusting for read-depth of the i-th sample and the length of the j-th gene [Mortazavi et al., 2008].

The primary challenge with studying RNA isoforms is that we cannot directly observe the expression of each RNA isoform. More specifically, an RNA-seq fragment may be compatible with more than one RNA isoform, and thus we cannot unambiguously assign it to an RNA isoform. Several methods have been developed to address this challenge [Jiang and Wong, 2009, Salzman et al., 2011, Richard et al., 2010, Xing et al., 2006, Trapnell et al., 2010, Roberts et al., 2011, Li et al., 2010, Katz et al., 2010, Pachter, 2011, Chen, 2012]. Moreover, the annotation of RNA isoforms may not be complete or accurate and thus one may need to reconstruct transcriptome annotation using RNA-seq data [Denoeud et al., 2008]. Simultaneous transcriptome reconstruction and isoform abundance estimation can be achieved using different approaches, including penalized regression methods [Xia et al., 2011, Bohnert and Rätsch, 2010, Li et al., 2011b,a], where each possible isoform is treated as a covariate in a regression problem. Interested readers are referred to Ala-mancos et al. [2014] for a comprehensive list of relevant statistical/computational methods.

Differential isoform expression (DIE) and differential isoform usage (DIU) are related but distinct concepts. DIE assesses the difference of absolute expression in isoform level. In contrast, DIU assesses the difference of relative expression in isoform level. For example, if the expression of two isoforms of one gene are 10 and 20 in control and 50 and 100 in case, then there is DIE but no DIU because the relative expression of the first isoform is 1/3 in both case and control. Although many methods have been developed to estimate RNA isoform expression, only a few methods have been developed to assess DIE or DIU while modeling biological variability and accounting for the uncertainty of isoform expression estimation. These methods include BitSeq [Glaus et al., 2012], Cuffdiff2 [Trapnell et al., 2013], and EBseq [Leng et al., 2013]. All three methods are designed for two-group or multi-group comparisons with multiple samples per group. BitSeq (Bayesian Inference of Transcripts from Sequencing data) adopts a two-stage approach. The first stage is isoform expression estimation within each sample using a Bayesian MCMC method. The second stage is to assess differential expression of each isoform using the posterior samples from the first stage. Cuffdiff2 employs a likelihood-based approach for isoform expression estimation and relevant hypothesis testing. For each gene, Cuffdiff2 first estimates expectation and covariance of the expression of multiple isoforms, and then uses these estimates to assess differential expression of this gene or DIU of its isoforms. For differential expression, Cuffdiff2 constructs a test statistic of log fold change, standardized by its standard error. Cuffdiff2 offers two tests for DIU: one for all the isoforms sharing a transcription starting site (TSS) and one for differential usage of TSSs. The test statistic for DIU is the square root of the Jensen-Shannon divergence, divided by its standard error. While both BitSeq and Cuffdiff2 first estimate isoform expression and then perform hypothesis testing, EB-Seq uses isoform expression estimates from other methods. For two-group or multi-group comparisons, EBSeq assumes the (rounded) isoform expression estimate follows a negative binomial distribution with group-specific mean and overdispersion. EBSeq stratifies all isoforms into multiple categories to allow category-specific mean-variance relations. These isoform categories are constructed based on the difficulty of isoform expression estimation. For example, genes with one, two, or more isoforms may form three categories.

BitSeq, Cuffdiff2, and EBseq all address an important issue for differential isoform expression (DIE): to account for the uncertainty inherent in the isoform expression estimation process. However, there are two types of commonly encountered tasks that cannot be accomplished by these methods: to assess DIE with respect to a continuous variable, e.g., age or additive coding of genotype (i.e., 0, 1, 2, for genotype AA, AB, and BB), and to assess DIE across two groups with only one sample per group, which is not an uncommon situation in real data studies. For example, one may wish to compare isoform expression between the paternal and maternal alleles of an individual or between normal and cancer tissues of a patient. In such situations, the RNA-seq data allow a valid statistical test, although the population for statistical inference is limited to the tested case and control (i.e., what happens if we collect more RNA-seq fragments from this case and this control) rather than the general case and control populations (i.e., what happens if we collect more samples from case or control population). BitSeq and EBseq cannot compare two groups with one case and one control. Cuffdiff2 provides an ad-hoc implementation for this problem. Specifically, when there is one case and one control, Cuffdiff2 estimates isoform expression variance by combining case and control, which implicitly assumes most isoforms are not differentially expressed. Therefore it is expected that Cuffdiff2 would yield conservative p-values and limited power in this situation, which is confirmed in our simulation studies.

In this paper, we develop a statistical method named IsoDOT, which assesses DIE or DIU using RNA-seq data and addresses the aforementioned two tasks that cannot be accomplished by existing methods. IsoDOT treats all the RNA isoforms of a gene (or a transcript cluster of a few overlapping genes) as a unit and tests whether any of these RNA isoforms is associated with a covariate of interest. Alternative strategies would be to assess differential expression or differential usage of each exon set or each RNA isoform. For testing at the exon set level, the number of tests is much larger than gene-level testing, which increases the burden on multiple testing correction. In fact, multiple testing correction is also more challenging because multiple exon sets of the same gene often have correlated expression. For isoform-level testing, the major challenge is to incorporate the uncertainty in isoform expression estimation into the testing step. It is possible that two isoforms are very similar and thus available data cannot distinguish them. Therefore differential expression testing for these two isoforms separately is problematic. By performing testing per transcript cluster, IsoDOT bypasses the limitation of exon-set-level or RNA-isoform-level testing. After transcript clusters with significant DIE or DIU are identified, one may follow up on these transcript clusters to identify differentially expressed exon sets [Anders et al., 2012] or isoforms [Glaus et al., 2012, Trapnell et al., 2013, Leng et al., 2013].

Materials and Methods

An overview

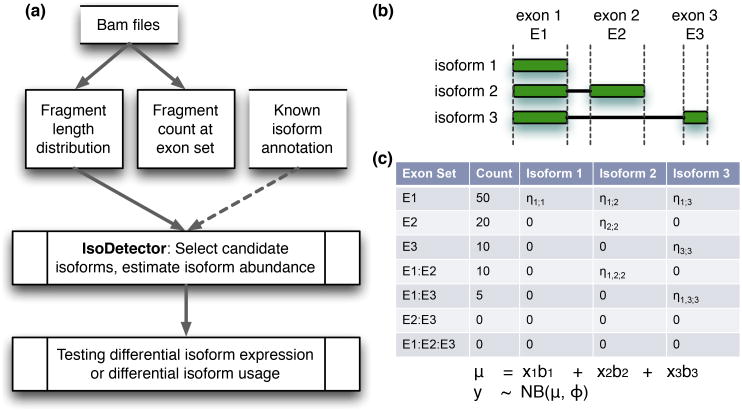
We assume that the locations and sizes of all the exons of a gene are known. If needed, one can use existing software (e.g., TopHat [Trapnell et al., 2009]) to detect previously unknown exons. The inputs of our method are the bam files of all samples. From each bam file, we derive the number of RNA-seq fragments overlapping each exon set (an exon set includes one or more adjacent or non-adjacent exons) and the distribution of RNA-seq fragments' lengths (Figure 1(a)). IsoDOT estimates RNA isoform expression across all samples, and outputs two p-values per gene: one for testing differential isoform expression (DIE) and one for testing differential isoform usage (DIU). The DIE test asks whether the absolute expression of any isoform of a gene is associated with the covariate of interest. In contrast, the DIU test asks, after adjusting for total expression of the corresponding gene, whether the relative expression of any isoform of this gene is associated with the covariate of interest.

Figure 1.

(a) IsoDOT work flow. The dash line indicates that known isoform annotation (i.e., transcriptome annotation) is optional, (b) A gene with 3 exons and 3 possible isoforms. (c) A matrix of input data. Each row corresponding to an exon set. The column “Count” is the number of RNA-seq fragments at each exon set, and the columns “isoform k” for k = 1,2,3 give the effective lengths of each exon set within each isoform, and specifically, η_A,k is the effective length of exon set A for the k-th isoform. NB(μ,φ) indicates a negative binomial distribution with mean μ, and dispersion parameter φ.

As part of IsoDOT, we have developed a penalized regression method, named IsoDetector, to estimate RNA isoform expression. In contrast to existing methods [Xia et al., 2011, Bohnert and Ratsch, 2010, Li et al., 2011b,a], IsoDetector employs penalized negative binomial regression with a log penalty. The negative binomial distribution is commonly used to model RNA-seq data, and previous studies have shown that it can account for variation in RNA-seq fragment counts across biological replicates [Langmead et al., 2010]. Many popular methods for differential expression testing, such as DEseq [Anders and Huber, 2010] and edgeR [Robinson et al., 2010], adopt such an assumption. More specifically, the negative binomial distribution assumption, denoted by N B(μ,φ), implies that the RNA-seq fragment count across biological replicates follows a negative binomial distribution with mean value μ and variance μ + μ²φ, where φ is an over-dispersion parameter. Therefore, the variance of a negative binomial distribution can be arbitrarily large for a large value of φ. The Log penalty, which can be interpreted as an iterative adaptive Lasso penalty [Tibshirani, 1996, Zou, 2006, Sun et al., 2010], is flexible enough to handle a broad class of penalization problems [Chen et al., 2014]. IsoDOT can test DIE/DIU against any categorical or continuous covariate at any sample size, with or without known isoform annotation. Our simulation and real data analysis demonstrate that IsoDOT performs very well with human or mouse RNA-seq data, but it can of course be applied to RNA-seq data from any species with a reference genome.

Two exons of a gene may overlap partially. In such situations, we split them into three exons: the part unique to the first or the second exon, and the part that belongs to both exons. Multiple genes may overlap on one or more exons, and we consider these genes as a transcript cluster, though any isoform of this transcript cluster can only be produced from one gene.

Isoform estimation in a single sample

We study the isoforms of each transcript cluster separately, and the following discussion applies to a specific transcript cluster. Denote the number of exons of a transcript cluster by k. Let A be an exon set, i.e., a subset of the k exons. Let y_iA be the number of sequence fragments that overlap and only overlap with all the exons of A in the i-th sample, where 1 ≤ i ≤ n, and n is the sample size. A sequence fragment overlaps with an exon if the “sequenced portion” of this fragment overlaps with at least 1 bp of the exon. For example, if a fragment is sequenced by a paired-end read where the first end overlaps with exon 1 and 2 and the second end overlaps with exon 4, then this fragment is assigned to exon set A = {1,2,4}.

To illustrate the main feature of our method, we consider a gene (which is a transcript cluster itself) with 3 exons and 3 isoforms (Figure 1(b)). Denote its expression at sample i by y_i = (y_i{1}, y_i{2}, y_i{3}, y_i{1,2}, y_i{2,3}, y_i{1,3}, y_i{1,2,3})^T. We assume y_iA follows a negative binomial distribution ψ(μ_iA,φ) with unknown mean μ_iA and dispersion parameter φ. Let μ_i be a column vector concatenating the μ_iA's, then μ_i = E(y_i). We model μ_i by:

$${\mathit{\mu }}_i={\mathbf{X}}_i\beta =\sum _{u=1}^p{\mathbf{x}}_{iu}{\beta }_u,{\beta }_u\ge 0,$$ (1)

where β_u is proportional to the transcript abundance of the u-th isoform, X_i = (x_i1, …, x_ip), and x_iu for 1 ≤ u ≤ p represents the effective lengths of all the exon sets for the u-th isoform in the i-th sample. Intuitively, effective length is the “usable length” for the data generation mechanism, i.e., the number of positions where a randomly selected sequence fragment can be sampled. The effective length of an exon set varies across the underlying isoforms. For example, isoforms 1 and 3 of the gene shown in Figure 1(b-c) do not include exon 2, and thus the effective length of exon set {2} is 0 for isoforms 1 and 3. In contrast, the effective length of exon 2 is nonzero for isoform 2, since it includes exon 2. In addition, effective length is also a function of the sample-specific RNA-seq fragment length distribution. The desired average length of RNA-seq fragments is often chosen during RNA-seq library preparation. However, the true fragment length distribution can be estimated from observed RNA-seq data. See Supplementary Materials Section A for details. In this example, the design matrix includes the effective lengths of all exon sets for isoforms 1, 2, and 3. Next, we recast the isoform estimation problem to a negative binomial regression problem with fragment counts y_i as response and effective lengths X_i as covariates:

$${\mathbf{y}}_i~\psi ({\mathit{\mu }}_i,\varphi ),\text{and}{\mathit{\mu }}_i={\mathbf{X}}_i\beta .$$ (2)

Equation (2) should be understood such that y_iA's are independent of each other and y_iA follows a negative binomial distribution ψ(μ_iA,φ). The independence assumption is reasonable because the fragment counts across exon sets should be independent given isoform configurations.

The regression problem presented in equation (2) is challenging because there can be a large number of possible isoforms and their effective lengths (e.g., the columns of the design matrix X_i) may be linearly dependent or significantly correlated. To address this difficulty, we first select a set of candidate isoforms, and then apply a penalized negative binomial regression to select the final set of isoforms from these candidate isoforms. The candidate isoforms can be selected using observed RNA-seq data (Supplementary Materials Section B) or a transcriptome annotation database (e.g., Ensembl [Flicek et al., 2011]).

In our analysis, we skip the exon sets that have zero or negligible effective lengths across all the candidate isoforms because these exon sets are not informative for isoform expression estimation. For example, the exon set {2,3} or {1,2,3} in the example shown in Figure 1 (c) are not included in the analysis. The number of candidate isoforms, denoted by p, can be much larger than the number of (informative) exon sets, denoted by m, and there may be high correlations among the effective lengths of the candidate isoforms. Therefore, selecting the final set of isoforms from the candidate isoforms is a challenging variable selection problem. Lasso penalty has been applied in previous studies. However, the selection consistency of Lasso requires an irrepresentability condition on the design matrix [Zou, 2006, Zhao and Yu, 2006], which posits that there are weak correlations between the “important covariates”, which have non-zero effects and the “unimportant covariates”, which have zero effects. This irrepresentability condition is often not satisfied for the isoform selection problem due to high correlations among candidate isoforms. We employ a Log penalty [Mazumder et al., 2011] for this challenging variable selection problem, which does not require the irrepresentability condition and can be interpreted as iterative adaptive Lasso [Sun et al., 2010, Chen et al., 2014]. The algorithm for fitting this penalized negative binomial regression is outlined in Supplementary Materials Section C.

Isoform estimation in multiple samples

To estimate isoform expression in multiple samples, we have to account for read-depth difference across samples. Let t_i be a read-depth measurement for the i-th sample. For example, t_i can be the total number of RNA-seq fragments in the i-th sample, or the 75 percentile of the number of RNA-seq fragments per gene in the i-th sample [Bullard et al., 2010]. We first consider a case without any covariate associated with isoform expression. To account for read-depth variation, we modify equation (1) to

$${\mathit{\mu }}_i=t_i{\mathbf{X}}_i\gamma =\sum _{u=1}^p{t}_i{\mathbf{x}}_{iu}{\gamma }_u,$$ (3)

where γ_u is proportional to relative expression of the u-th isoform, after normalizing by t_i.

Let ${\mathbf{y}}^{\mathbf{T}}=({\mathbf{y}}_1^{\mathbf{T}},\dots ,{\mathbf{y}}_n^{\mathbf{T}})$, ${\mathit{\mu }}^{\mathbf{T}}=({\mathit{\mu }}_1^{\mathbf{T}},\dots ,{\mathit{\mu }}_n^{\mathbf{T}})$, and ${\mathbf{Z}}^{\mathbf{T}}=(t_1{\mathbf{X}}_1^{\mathbf{T}},\dots ,t_n{\mathbf{X}}_n^{\mathbf{T}})$, where y and μ, are vectors of length nm and Z is a matrix of size nm × p. Recall that p is the number of candidate isoforms, n is sample size, and m is the total number of exon sets. Then the isoform selection problem can be written as a negative binomial regression problem

$$\mathbf{y}~\psi (\mathit{\mu },\varphi )\text{and}\mathit{\mu }=\mathbf{Z}\gamma ,\text{where}{\gamma }_j\ge 0\text{for}1\le j\le p.$$ (4)

After imposing a penalty, we solve this regression problem using the method described in Supplementary Materials Section C.

Next we consider isoform estimation given a continuous covariate g = (g₁, …, g_n)^T. We assume the expression of an isoform u for sample i, denoted by γ_iu, is a linear function of covariate g_i: γ_iu = a_u + b̃_ug_i. This linear model is an appropriate choice when g_i represents SNP genotype [Sun, 2012], which is the focus of our empirical data analysis. In this linear model setup, a complex set of constraints is needed for a_u and b̃_u so that γ_iu ≥ 0 for any value of g_i. Therefore we reformulate the problem as follows. Without loss of generality, we scale the value of g_i to be within the range of [0,1] with the minimum and maximum values being exactly 0 and 1, respectively. For example, if g_i corresponds to a SNP with additive effect, we can set g_i = 0, 0.5, or 1 for genotype AA, AB, or BB. Let b_u = b̃_u + a_u, then γ_iu = a_u + (b_u − a_u)g_i = a_u(1 − g_i) + b_ug_i. Under this model, we have

$${\gamma }_{iu}\ge 0\text{for any}{g}_i\in [0,1]\iff a_u\ge 0\text{and}{b}_u\ge 0.$$

Let a = (a₁,…, a_p)^T and b = (b₁,…, b_p)^T, we have

$${\mathit{\mu }}_i=t_i{\mathbf{X}}_i[\mathbf{a}(1-g_i)+\mathbf{b}{g}_i\mathbf{]}.$$ (5)

By concatenating a and b into a vector: θ = (a₁, …, a_p,b₁, …,b_p)^T, we can rewrite equation (5) as μ_i = W_iθ, where W_i = [t_iX_i(1 − g_i), t_iX_ig_i] is an m × 2p matrix. Let ${\mathbf{W}}^{\mathbf{T}}=({\mathbf{W}}_1^{\mathbf{T}},\dots ,{\mathbf{W}}_n^{\mathbf{T}})$, then the isoform expression estimation problem reduces to a negative binomial regression problem with non-negative coefficients

$$\mathbf{y}~\psi (\mathit{\mu },\varphi )\text{and}\mathit{\mu }=\mathbf{W}\mathit{\theta },\text{where}{\theta }_j\ge 0\text{for}1\le j\le 2p.$$ (6)

After imposing a penalty, we solve the resulting penalized regression problem by the coordinate ascend method described in Supplementary Materials Section C.

Finally we consider the general situation with q covariates, denoted by g₁,…, g_q, where g_v = (g_1v, …,g_nv)^T for v = 1, …,q. Without loss of generality, we assume 0 ≤ g_iv ≤ 1 for 1 ≤ i ≤ n and 1 ≤ v ≤ q. Then we model γ_iu by ${\gamma }_{iu}=q{a}_u+{\sum }_{v=1}^q(b_{vu}-a_u)g_{iv}=a_u{\sum }_{v=1}^q(1-g_{iv})+{\sum }_{v=1}^q{b}_{uv}{g}_{iv}$. This is simply a multiple linear regression model where each covariate g_v has its own effect. Let a = (a₁,…, a_p)^T and b_v = (b_1v,…, b_pv)^T, then

$${\mathit{\mu }}_i=t_i{\mathbf{X}}_i[\mathbf{a}\sum _{v=1}^q(1-g_{iv})+{\mathbf{b}}_1{g}_{i1}+\cdots +{\mathbf{b}}_q{g}_{iq}].$$ (7)

By concatenating a, b₁, b₂, …, b_q into a vector: $\mathit{\theta }={({\mathbf{a}}^{\mathbf{T}},{\mathbf{b}}_1^{\mathbf{T}},\dots ,{\mathbf{b}}_q^{\mathbf{T}})}^{\mathbf{T}}$, we rewrite the above equation as μ_i = W_iθ, where ${\mathbf{W}}_i=[t_i{\mathbf{X}}_i{\sum }_{v=1}^q(1-g_{iv}),t_i{\mathbf{X}}_i{g}_{i1},\cdots ,t_i{\mathbf{X}}_i{g}_{iq}]$ is an m × (q + 1)p matrix. Let ${\mathbf{W}}^{\mathbf{T}}=({\mathbf{W}}_1^{\mathbf{T}},\dots ,{\mathbf{W}}_n^{\mathbf{T}})$, then we form an negative binomial regression problem

$$\mathbf{y}~\psi (\mathit{\mu },\varphi )\text{and}\mathit{\mu }=\mathbf{W}\mathit{\theta },\text{for}{\theta }_j\ge 0,1\le j\le (q+1)p.$$ (8)

After imposing a penalty on each θ_j, we can solve the resulting penalized regression problem by the coordinate ascend method described in Supplementary Materials Section C.

When studying multiple samples, it is possible that an exon set is only expressed in a subset of samples. Therefore, when examining the fragment counts of this exon set across all samples, there are more 0's than expected by a negative binomial distribution. In such case, we introduce a zero-inflated component and employ the zero-inflated negative binomial distribution [Rashid et al., 2011] to model RNA-seq fragment count data.

Testing for differential isoform expression (DIE)

We have described the statistical model to estimate RNA isoform expression in multiple samples given one or more covariate. Building on this model, we assess differential isoform expression with respect to a set of covariates denoted by V using a likelihood ratio test. Specifically, the null hypothesis (H₀) is that b_uv = a_u for u = 1, …,p and v ∊ V and the alternative hypothesis (H₁) is that b_uv ≠ a_u for at least one pair of (u, v), where u = 1, …,p and v ∊ V. It is helpful to understand this test by considering two special cases. First, we assume there is only one numerical covariate. Under H₀, we solve the isoform estimation problem by a penalized negative binomial regression with expected value μ_i = t_iX_ia. Under alternative, μ_i = t_iX_i[a(1 − g_i) + bg_i]. Therefore the number of parameters is p under H₀ and 2p under H₁. The asymptotic Chi-square distribution with degree of freedom p does not apply because the models are estimated, under both H₀ and H₁, by penalized regression. In the second special case, we assume the only variable of interest is a categorical variable with d categories. This categorical variable can be coded as d − 1 binary variables, dented by g_i1,…, g_i,d−1. The expected values of fragment counts across exon sets under H₀ and H₁ are μ_i = (d − 1)t_iX_ia and ${\mathit{\mu }}_i=t_i{\mathbf{X}}_i[\mathbf{a}{\sum }_{v=1}^{d-1}(1-g_{iv})+{\mathbf{b}}_1{g}_{i1}+\cdots +{\mathbf{b}}_{d-1}{g}_{i,d-1}]$, respectively. Therefore the number of parameters under H₀ and H₁ are p and dp, respectively. Again, the asymptotic Chi-square distribution with degree of freedom (d − 1)p does not apply because the models are estimated, under both H₀ and H₁, by penalized regression.

We use likelihood ratio (LR) statistic as our test statistic:

$$\mathcal{L}\mathcal{R}=2({\mathit{\ell }}_1-{\mathit{\ell }}_0),$$

where ℓ₀ and ℓ₁ are the log likelihoods under null and alternative, respectively. Because of penalized estimation, the null distribution of this test statistic no longer follows the standard asymptotic distribution. We obtain the null distribution by parametric bootstrap or permutation. The parametric bootstrap approach proceeds as follows. (1) Fit the penalized negative binomial regression under null. (2) Sample fragment counts based on the fitted null model. (3) Using the sampled counts to refit models under null and alternative and calculate the LR statistic. (4) Repeat steps (1)-(3) a large number of times as needed [Jiang and Salzman, 2012]. (5) Calculate the p-value as the proportion of the bootstrapped LR statistics that are larger than . This parametric bootstrap procedure yields valid p-values regardless of the sample size n. However, since the sampling population is all the RNA-seq fragments from the studied samples, small p-values only imply a significant difference of the studied samples and should not be generalized to other individuals.

If sample size is sufficiently large (e.g., ≥ 5 cases vs. ≥ 5 controls), we can obtain valid statistical inference for the corresponding population (instead of studied samples) by calculating permutation p-values. Specifically, the null model is fitted without the covariate of interest, and thus its log likelihood l₀ remains unchanged across permutations. In each permutation, we permute the covariate of interest and refit the alternative model, and then calculate the likelihood ratio test statistic. We repeat this process a large number of times to obtain a null distribution of the likelihood ratio statistic.

Testing for differential isoform usage (DIU)

All the previous discussion, including RNA isoform expression estimation and differential isoform expression testing, focus on absolute expression of RNA isoforms, which is RNA isoform expression after correcting for read-depth variation across samples. Another measure of RNA isoform expression, which may be more interesting in many situations, is the relative expression with respect to the total expression of the corresponding gene or transcript cluster. This is because a gene may have higher or lower expression overall, and it may also switch the usage of some RNA isoforms. For example, a gene may predominately use one isoform in one tissue and switch to another isoform in another tissue. Such relative expression of an RNA isoform is referred to the isoform usage. For a transcript cluster of interest, we denote the total number of RNA-seq fragments in the i-th sample by r_i. Recall that in the previous discussions of DIE, t_i denotes a read-depth measurement for the i-th sample. To assess DIU, we apply the same procedure as assessing DIE, except that we replace t_i by r_i.

Results and Discussions

Simulation for case-control comparison

We simulated ∼1 million 76 + 76 bps paired-end RNA-seq reads for a single case and control sample respectively using Flux Simulator (http://flux.sammeth.net/simulator.html) and the Ensembl transcriptome annotations (version 67, http://useast.ensembl.org/info/data/ftp/index.html) for chromosome 1 (chr1) and chromosome 18 (chr18) for the mouse genome. We simulated the data such that all genes from chr1 were equivalently expressed and all genes from chr18 were differentially expressed, either in terms of total expression or isoform usage (Supplementary Figure 2). These simulated RNA-seq reads were mapped to the reference genome using Tophat [Trapnell et al., 2009]. Next, we counted the number of RNA-seq fragments per exon set. It was important to consider all exon sets rather than just exon or exon junctions because many RNA-seq fragments overlap with more than two exons. For example, in this simulated dataset, ∼27% of the paired-end reads overlapped 3 or more exons (Supplementary Figure 3). In addition, we confirmed that the number of sequence fragments per exon set was proportional to the effective length of the exon set (Supplementary Figure 4).

The dimension of this problem (i.e., the number of exon sets m versus the number of candidate isoforms p) was illustrated in Supplementary Figures 5-6. Given transcriptome annotation, p < m for the vast majority of transcript clusters, and without transcriptome annotation, we restricted the number of candidate isoforms so that approximately p < 10m. In either case, there were strong correlations among the candidate isoforms (Supplementary Figures 7-8), therefore necessitating the use of penalized regression in IsoDetector. After applying penalized regression, most transcription clusters included 10 or fewer isoforms, with or without transcriptome annotation (Supplementary Figures 9-10).

We compared isoform abundance estimates from IsoDetector and Cufflinks (v2.0.0) [Trapnell et al., 2010, 2013] using the case sample. The conclusions from the control sample were similar (results not shown). We focused on 1,062 transcript clusters (corresponding to 5,185 transcripts) that had at least 2 exons with ≥5 sequence fragments overlapping each exon. Most of these transcript clusters included 1-2 genes and 1-42 transcripts, and most of the 5,185 transcripts harbored 6-500 RNA-seq fragments (Figure 2a). If transcriptome annotation was unavailable, the isoforms selected by IsoDetector were more similar to the true ones than Cufflinks (Figure 2b). The two methods had similar accuracy in terms of transcript abundance estimation, either with (Figure 2c-2d) or without (Figure 2e-2f) transcriptome annotation.

Figure 2.

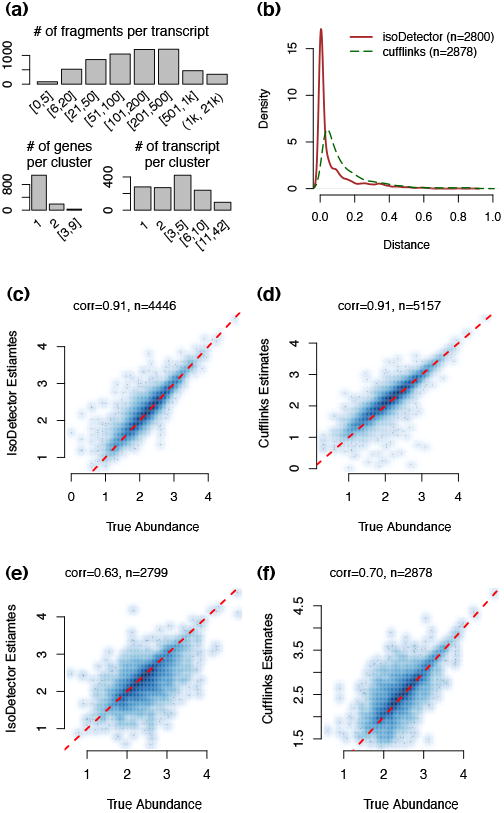
(a) A summary of the RNA-seq data and annotation of the simulated case sample. (d) Density curves of the distance between each de novo transcript and its closest transcript from transcriptome annotation. The distance is defined as the ratio of the number of unmatched base pairs over the total number of base pairs covered by either isoform. A base pair is “matched” if it corresponds to an exon or intron location for both isoforms. (c-d) Comparison of true transcript abundance vs. estimates from IsoDetector or Cufflinks when we use known isoform annotation. Both X and Y-axes are in log₁₀ scale. “n” is the number of transcripts with status “OK” for either IsoDetector or Cufflinks. (e-f) Comparison of true transcript abundance vs. estimates from IsoDetector or Cufflinks when we do not use any isoform annotation.

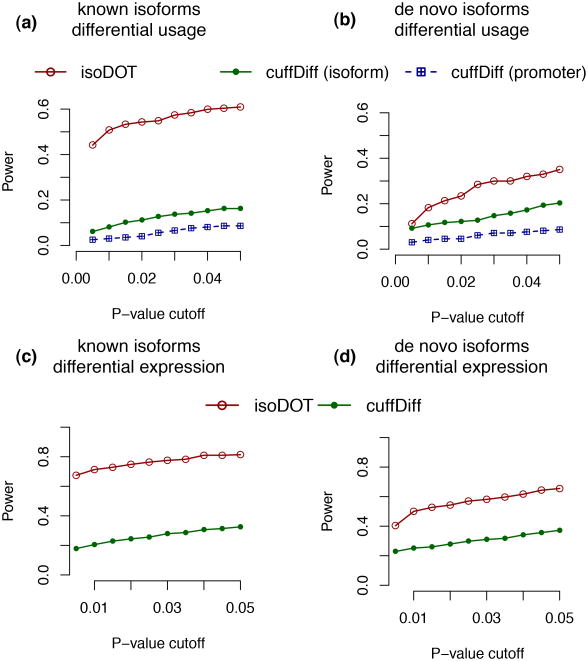
We next compared the power of IsoDOT to that of Cuffdiff (v2.0.0) [Trapnell et al., 2013] in terms of testing for differential expression or differential isoform usage. Cuffdiff results were obtained from three files: gene_exp.diff (differential expression), splicing.diff (differential usage of the isoforms sharing a transcription start site (TSS)), and promoters.diff (differential usage of TSSs). The majority of the genes in file gene_exp.diff have status “OK” and they were used in the following comparison. However, no gene has status “OK” in file splicing.diff or promoters.diff. In these two files, all the genes with meaningful p-values have status “NOTEST”, indicating that Cuffdiff recommends users not to trust these testing results. The reason is as follows. For a two group comparison with one case and one control, Cuffdiff combines the case and the control to estimate variance of biological replicates, which leads to a very conservative p-value since this approach implicitly assumes the case and the control have the same expected value. Nonetheless, these genes with status “NOTEST” were used in the following comparison because they are the only genes that we can use. A gene could have multiple p-values in splicing.diff. In favor of Cuffdiff for power comparison, we used the smallest p-value for each gene. Based on our simulation setup, power was defined as the proportion of the genes from chr18 that had significant DIE or DIU. IsoDOT had substantially higher power than Cuffdiff (Figure 3), attributed to the correct type I error control of IsoDOT (Supplementary Figure 11). The poor performance of Cuffdiff is not simply a calibration issue because IsoDOT still performs better than Cuffdiff when we compare two methods using ROC curves (Supplementary Figure 12). Instead, the poor performance of Cuffdiff is because it tries to estimate variance across biological replicates when there is no biological replicate at all. IsoDOT can perform a valid test because it does not try to estimate variance of biological replicates. Instead, it tries to estimate the variance due to resampling of RNA-seq reads. To be fair, Cuffdiff does recommend such test with one case versus one control and we include Cuffdiff in our comparison because it is the only method that allows for such testing. In conclusion, this simulation illustrated that IsoDOT worked well in this challenging situation of comparing one case vs. one control.

Figure 3.

Compare the power of IsoDOT and Cuffdiff for detesting genes with differential isoform usage (a-b) or differential isoform expression (c-d), while transcriptome annotation is known (a,c) or not (b,d).

Simulation for isoform usage eQTL

To illustrate the performance of IsoDOT in testing differential isoform usage with respect to a continuous covariate, we applied IsoDOT to map isoform usage eQTL (gene expression quantitative trait locus) using simulated RNA-seq data and real genotype data. We downloaded genotype data from 60 European HapMap samples [Thorisson et al., 2005] and selected 949,537 SNPs with minor allele frequency (MAF) > 0.05 for the following analysis. We defined transcription clusters based on Ensembl annotation (version 66, http://useast.ensembl.org/info/data/ftp/index.html), and selected 200 transcript clusters that satisfied the following two conditions for our simulation studies. (1) Each transcript cluster has > 1 annotated RNA-isoforms, and (2) Each transcript cluster has ≥ 1 SNP in the gene body (any intronic or exonic regions) or within 1000bp of the gene body. For each selected transcript cluster, we simulated RNA-seq fragment counts across exon sets under null (H₀) and alternative (H₁), respectively. Specifically, for each gene, we randomly selected 50% of the isoforms to have zero expression and set the expression of the other 50% of isoforms by drawing γ_u (equation (4)) from a uniform distribution U[0.5, 1].

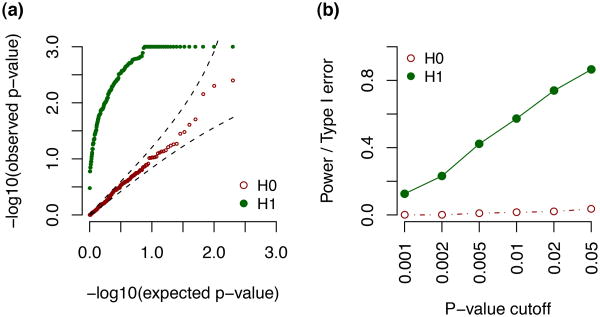
Next, we used these simulated data to assess differential isoform usage of each transcript cluster with respect to each of the nearby SNPs (within 1000bp of the gene body) and kept the most significant eQTL per transcript cluster. For each transcript cluster, up to 1000 permutations were carried out to correct for multiple testing across the multiple nearby SNPs. Under H₀, the permutation p-values followed a uniform distribution; and under H₁, the permutation p-values were obviously enriched with small values (Figure 4(a)). In this simulation, we had ∼ 80%/40% power to detect local isoform usage eQTL for permutation p-value cutoffs 0.05 and 0.005, respectively (Figure 4(b)). Therefore, this simulation demonstrates that IsoDOT correctly controls type I error and has power to detect differential isoform usage with respect to a continuous covariate.

Figure 4.

Simulation results for testing isoform-usage eQTL on 200 transcription clusters. (a) The qq-plot for p-values distributions against expected uniform distribution. (b) Power (H1) or type I error (H0) for different p-value cutoffs.

Haloperdiol treatment effect on mouse transcriptome

Haloperidol is a drug used to treat schizophrenia, acute psychotic states, and delirium. A major adverse side effect of chronic haloperidol treatment is tardive dyskinesia (TD). TD can be modeled in mice be examining haloperidol-induced vacuous chewing movements (VCMs) [Crowley et al., 2012]. We applied IsoDOT to analyze RNA-seq data for mice treated with haloperidol vs. placebo with particular interest in identifying genes responding to haloperidol treatment and/or responsible for VCM. RNA-seq data were collected from whole brains from four mice: two C57BL/6J mice treated with haloperidol or placebo and two 129S1Sv/ImJ×PWK/PhJ F1 mice treated with haloperidol or placebo. Each RNA-seq fragment was sequenced on both ends by 93 or 100bp, and 20-27 million RNA-seq reads were collected for each mouse (Supplementary Table 1). See Supplementary Materials Section D for additional details of the experiment.

We first studied differential isoform expression/usage between two C57BL/6J mice. RNA-seq reads were mapped to the mm9 reference genome using TopHat [Trapnell et al., 2009]. At FDR of 5%, IsoDOT identified 86 or 88 genes with differential isoform usage (DIU), with or without transcriptome annotation, respectively. For the test of differential isoform expression (DIE), also at FDR of 5%, IsoDOT identified 332 or 206 genes with or without transcriptome annotation, respectively. We sought to gain some insight of these four gene lists by applying functional category enrichment analysis [Sherman et al., 2009] on the top 100 genes in each list. Only those DIU genes identified with transcriptome annotation were significantly associated with biologically relevant categories such as neuron projection (Supplementary Figure 13-16). This implied that DIU, rather than DIE, might be more relevant to haloperidol treatment in C57BL/6J mice. The gene lists identified without transcriptional annotation did not show functional enrichment, which implied larger sample size or higher read-depth were needed to detect DIE or DIU without transcriptome annotation. According to Cuffdiff manual, it is not recommended to run Cuffdiff with sample size one versus one. However, we still evaluated the performance of Cuffidff in this dataset for comparison purpose. Using the results reported by Cuffdiff, no gene has q-value smaller than 0.05 (with or without annotation, alternative promoter or alternative splicing), and functional category enrichment analysis [Sherman et al., 2009] on the top 100 genes reported by Cuffdiff identified no significantly enriched functional category (Supplementary Figure 17).

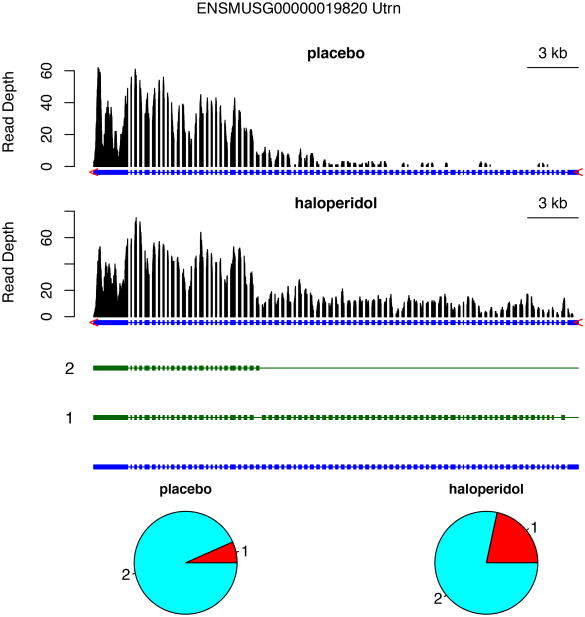
Several DIU genes identified by IsoDOT can be potential targets for follow up studies (Supplementary Table 2). For example, Utrn (utrophin, Figure 5) and Dmd (dystrophin) are both involved in neuron projection and could be candidates underlying the VCM side effect. Grin2b (glutamate receptor, ionotropic, NMDA2B, Supplementary Figure 18) or its human ortholog is involved in Alzheimer's disease, Huntington's disease, and amyotrophic lateral sclerosis (ALS), which are potentially relevant to the VCM side effect of haloperidol treatment. In addition, our previous studies had prioritized several other glutamate receptors such as Grin1 and Grin2a as candidates that response to haloperidol treatment using independent data and methods [Crowley et al., 2012].

Figure 5.

Differential isoform usage of gene Utrn between a mouse with haloperidol treatment and a mouse with placebo. The top panel shows the read-depth of RNA-seq reads in two conditions. Two annotated isoforms and all the exons are illustrated in middle panel. The expression of each isoform under two conditions are shown in the bottom panel.

Similar studies were conducted for the two F1 mice of 129S1Sv/ImJ×PWK/PhJ. To better map RNA-seq reads, we first built two pseudogenomes for 129S1Sv/ImJ and PWK/PhJ by incorporating Sanger SNPs and indels [Keane et al., 2011] into the reference genome and mapped RNA-seq reads to the two pseudogenomes separately. Next, alignments were remapped back to the reference coordinate system and the observed genetic variants were annotated for each RNA-seq fragment. IsoDOT identified much less DIU or DIE genes in these two F1 mice than in the two C57BL/6J mice. At FDR 0.2, no DIU genes were identified and 85 DIE gene were identified. Six of these 85 genes were involved in actin-binding, though this functional category was not significantly overrepresented.

The greater level of DIE and DIU in C57BL/6J than 129S1Sv/ImJ×PWK/PhJ following chronic haloperidol treatment was consistent with behavioral phenotype data which showed that C57BL6/J mice had greater susceptibility to haloperidol-induced VCM (Supplementary Figure 19) [Crowley et al., 2012]. Therefore, some of the C57BL/6J transcriptional changes detailed in this study might contribute to the development of haloperidol-induced VCM.

Allele-specific differential isoform usage

About 37.2% of the RNA-seq fragments from the two 129S1Sv/ImJ×PWK/PhJ F1 mice were only mapped to the paternal or maternal allele or were mapped to one allele with fewer mismatches, and hence they were allele-specific RNA-seq fragments. There was no genome-wide bias, i.e., ∼50% of the allele-specific RNA-seq fragments were mapped to each parental strain (Supplementary Table 1). Using these allele-specific RNA-seq fragments, we applied IsoDOT to assess differential isoform usage between maternal and paternal alleles. At a liberal FDR cutoff 0.2, no DIU gene was identified, and 19 or 30 DIE genes were identified from the haloperidol/placebo treated F1 mice, respectively. The genes with significant differential isoform usage in the haloperidol treated mice, but not the placebo treated mice might indicate genetic×treatment interactions. Supplementary Table 3 listed 23 such genes with DIU p-values < 0.01 in the haloperidol treated mice, and DIU p-values > 0.1 in the placebo treated mice. Among them, Synpo and Snap25 are associated with neuron functions. Snap25 is known to be associated with schizophrenia and/or haloperidol treatment at DNA [Müller et al., 2005], RNA [Sommer et al., 2010], and protein levels [Thompson et al., 1998, Honer et al., 2002]. To the best of our knowledge, this is the first report that the differential isoform usage of Snap25 is associated with genetic×haloperidol treatment interaction.

Software and data availability

An R package of IsoDOT is available at http://www.bios.unc.edu/∼weisun/software/isoform.htm. Testing differential isoform expression/usage is computationally intensive. Using IsoDOT with up to 1,000 parametric bootstraps, it will take on average 1-3 minutes to test differential isoform usage for a gene on a single processor. Parallel computation is needed and straightforward for genome-wide study. We are also actively working on implementing our method using Graphics Processing Unit (GPU) using the massively parallel algorithm described in Supplementary Materials Section E. Simulated RNA-seq data can be downloaded from http://www.bios.unc.edu/∼weisun/software/isoform_files/. The RNA-seq data of mouse haloperidol treatment experiment are available from NCBI GEO (GSExxx).

Discussion

We have developed a new statistical method named IsoDOT to assess differential isoform expression or usage from RNA-seq data with respect to categorical or continuous covariates. The resampling based approach is the basis of our hypothesis testing method. Two components of our method, the negative binomial distribution assumption and the Log penalty for penalized estimation are important for the success of this resampling based approach. First, the negative binomial distribution is a well-accepted choice for modeling RNA-seq fragment data across biological replicates. For the completeness of our paper, we also demonstrate that the negative binomial distribution provides a good fit of RNA-seq fragment counts, while the Poisson distribution assumption leads to a severe underestimate of variance (Supplementary Figure 20). Replacing the Log penalty with the Lasso penalty in IsoDOT leads to inaccurate type I error control and/or reduced power (Supplementary Figure 21). The limitation of Lasso is especially apparent when we do not use isoform annotation, where the number of candidate isoforms is much larger than sample size. This is consistent with previous findings that Lasso tends to select more false positives and has larger bias in effect estimates than the Log penalty [Chen et al., 2014].

Some biases should be accounted for to obtain better estimates of RNA isoform abundance. For example, the RNA-seq reads may not be uniformly distributed along the transcript, and DNA sequence features such as GC content may affect the abundance of RNA-seq reads. Such biases, if they exist, affect both the likelihoods under the null and alternative hypotheses and do not alter our Type I error rate. Furthermore, it may have limited impact on power because we calculate p-values through resampling approaches. For example, if the last exon of a gene tends to have a larger number of RNA-seq reads, our method may overestimate the expression of the isoform harboring the last exon. However, such over-estimation occurs under both the null and alternative hypotheses and, therefore, does not lead to inflated or deflated type I error. Systematically accounting for such biases are among our future plans to improve IsoDOT?s performance.

A major strength of IsoDOT is that it allows the assessment of differential isoform usage between one case and one control sample. This is especially important for paired samples, e.g., maternal and paternal alleles of one individual. When there are multiple paired samples, we can combine the p-values of multiple pairs using meta-analysis via Fisher's method or Stouffer's Z-score [Hunter et al., 1982]. In the preliminary study reported in this paper, we have identified several interesting genes (Utrn, Dmd, Grin2b, Snap25) whose isoform usage may respond to haloperidol treatment and are perhaps related to its side effects. In the near future, we plan to extend this study to include a much larger number of mice with diverse genetic backgrounds including mice from the Collaborative Cross [Churchill et al., 2004, Consortium, 2012].

Recently developed sequencing techniques can now deliver longer reads, including 2 × 250 bp reads from Illumina's MiSeq or 400 bp reads from Ion Torrent. Our methods can handle these longer sequencing reads without any difficulty. In fact, when the RNA-seq reads are long enough, transcriptome reconstruction becomes much easier. However, until all the isoforms of a transcript cluster can be unambiguously reconstructed and all the RNA-seq fragments can be assigned to an isoform with (almost) 100% certainty, testing differential isoform expression/usage remains a challenging problem where methods and software such as IsoDOT are needed. Another recently developed RNA-seq technique is to deliver “stranded” sequences so that RNA-seq from sense and antisense strands are separated. For the analysis of such stranded RNA-seq data, the only step in the IsoDOT pipeline that needs to be modified is to count the RNA-seq fragments for sense and anti-sense strands separately.