An unexpected finding: younger fathers have a higher risk for offspring with chromosomal aneuploidies

Abstract

The past decades have seen a remarkable shift in the demographics of childbearing in Western countries. The risk for offspring with chromosomal aneuploidies with advancing maternal age is well known, but most studies failed to demonstrate a paternal age effect. Retrospectively, we analyzed two case data sets containing parental ages from pre- and postnatal cases with trisomies 21, 13 and 18. The reference data set contains the parental ages of the general Swiss population. We dichotomized all couples into two distinct groups. In the first group, the mothers' integral age was as least as the father's age or older. We compared the frequency of cases in nine 5-year intervals of maternal age. In addition, we computed logistic regression models for the binary endpoint aneuploidy yes/no where paternal ages were incorporated as linear or quadratic, as well as smooth functions within a generalized additive model framework. We demonstrated that the proportion of younger fathers is uniformly different between cases and controls of live-born trisomy 21 as well, although not reaching significance, for fetuses over all mother's ages. Logistic regression models with different strategies to incorporate paternal ages confirmed our findings. The negative paternal age effect was also found in pre- and postnatal cases taken together with trisomies 13 and 18. The couples with younger fathers face almost twofold odds for a child with Down syndrome (DS). We estimated odds curves for parental ages. If confirmation of these findings can be achieved, the management of couples at risk needs a major correction of the risk stratification.

Introduction

The past decades have seen a remarkable shift in the demographics of childbearing parents in Western countries.¹ The progressively advancing parental age negatively influences the outcome of pregnancy by reducing fertility and increasing the number of miscarriages and stillbirths, the risk for chromosomal abnormalities and maternal factors such as hypertensive complications.² The risk for miscarriages is highest if both partners are advanced in age. Older couples comprising a woman aged ≥35 years and of a man ≥40 years have an at least fivefold higher risk for miscarriages.³ The significant effect of advancing maternal age on the risk of chromosomal abnormalities is well known, and several studies showed an exponential increase in the risk for an offspring with Down syndrome (DS) or another chromosomal aneuploidy.^{4, 5} The decrease in the quality of the oocyte with advancing maternal age is thought to be responsible for both the decline in fertility and the increasing risk of chromosomal abnormalities.^{1, 2} Recent experience with in vitro fertilization using donor oocytes from younger women supports this hypothesis.⁶ Therefore, one concluded that for risk assessment for aneuploidies the maternal age is the major factor.

A causative paternal age effect was more difficult to demonstrate, as paternally derived extra chromosomes account only for 5–10% of DS cases.^{7, 8} Most studies failed to demonstrate a paternal age effect,^{8, 9, 10, 11, 12, 13} or the significant age effect was limited to paternal age groups of >40 years.^{14, 15, 16, 17, 18, 19, 20} However, there is a major paternal factor influencing fertility and number of live births in the general population.³ The pathogenesis and the impact of paternal contribution to intrauterine survival of these conceptions is an important one that needs additional research.

In our retrospective study, we analyzed maternal and paternal ages of 1 932 927 live births born in Switzerland in the years from 1979 to 2006. We determined the reference distribution of maternal and paternal age in couples with a successful live birth and found an outstanding ‘demographic' paternal age effect. With advancing maternal age, the proportion of fathers with a higher age than their spouses decreased dramatically. Therefore, we postulated that also in couples with a child with aneuploidy this biological paternal age effect should exist and tested this hypothesis in two independent study groups with autosomal aneuploidies. In the DS study group, we compared the parental age in pre- and postnatal cases with trisomy 21. In the second study group we analyzed parental ages from pre- and postnatal cases of trisomy 13 (Patau syndrome) and trisomy 18 (Edwards syndrome).

Materials and Methods

Procedures

The reference data set contains the parental ages from live births from all married couples in Switzerland. It was obtained from the Federal Office of Statistics at Berne, Switzerland. Since 1979 the maternal and paternal ages of married couples were registered. The proportion of married couples from all couples with live births slightly decreased from 95.6% in 1979 to 84.6% in 2006. Finally, parental ages are available from 1 932 927 of the total 2 099 237 live births (92.1%) in the time period from 1979 to 2006.

The two case data sets contain parental ages rounded to integer years from pre- and postnatal cases with trisomy 21, with trisomy 13 and trisomy 18. From all samples, metaphase chromosome preparations had been performed according to standard procedures at the Institute of Medical Genetics in Zurich. Parts of the clinical data have been published previously.^{21, 22} Only cases with free aneuploidies and complete information of the parental ages had been included. At the end, the DS study group includes 198 prenatal and 559 postnatal cases with trisomy 21 (corresponds approximately to 15.7% of all estimated postnatal DS cases (N=3561) in Switzerland between 1979 and 2006⁴). A total of 20 pre- and 42 postnatal cases with trisomy 13 and 49 pre- and 101 postnatal cases with trisomy 18 fulfilled criteria for inclusion into the independent confirmation study group. The couples from all cases were living in the eastern half of Switzerland (cantons of Appenzell, Aargau, Glarus, Grisons, Lucerne, Sankt Gallen, Schaffhausen, Schwyz, Ticino, Thurgau, Unterwalden, Uri, Zug, Zurich). It is important to note that the births in the postnatal case data sets are a subset of the births in the original reference data set.

Statistical methods

As a first approach, we dichotomized all couples. In the first group the mother's age was at least the father's age (group 1: m.≥f.) and in the second group the father was older than the mother (group 2: m.<f.). We compared the proportion of cases in the two groups in 5-year intervals of maternal age (that is, 10–14, 15–19, 20–24 and so on, totally nine age groups) using Fisher's exact test. To correct for multiple testing in all these age groups, we use a Bonferroni-corrected significance level, that is, α*=α/9=0.0056 for a global significance level α=0.05. Odds ratios and Bonferroni-corrected confidence intervals (that is, at a confidence level of 1−(α/9)) for each maternal age category were calculated.²³ To get an idea about the uncertainty in estimating proportions, we computed Wilson-confidence intervals (Wilson CIs) at the Bonferroni-corrected level α*. The analyses were conducted on the independent study groups and on the pooled samples with trisomy 13, 18 and 21.

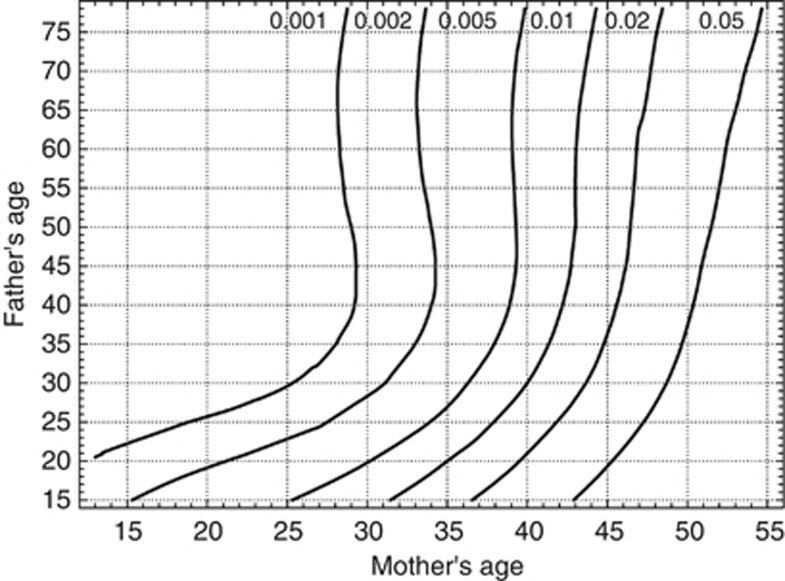
As a step towards quantification of the effects and explicitly modeling and visualizing the dependence of the odds for aneuploidy on parental ages, we computed three logistic regression models for the binary endpoint ‘aneuploidy yes/no'. As a first model, and to get an idea about the form of the dependence of the odds for aneuploidy, we computed a generalized additive model (GAM),^{24, 25} where parental ages were considered smooth effects each (model not shown) and jointly. Inspired by the forms of these dependencies we then generated simpler models with either both parental ages considered linear or linear plus quadratic. Using these simple models we are then able to provide estimates of odds ratios and corresponding 95% profile likelihood confidence intervals for aneuploidy for different scenarios of the parental ages. Effect quantification using the GAMs with the joint smooth effect was then received via computing predictions for the odds for aneuploidy, for all parental age combinations, see Figure 1. GAMs were computed with R²⁶ using the package mgcv,²⁷ with default settings for the smoothing parameters, see also Wood.²⁸ We got models that are sufficiently convenient to interpret; therefore, we did not consider father's–mother's age interactions in our models.

Figure 1.

Estimated odds for Down syndrome as a function of parental ages.

To conclude, it is important to note that absolute values of estimated odds in Figure 1 need to be taken with caution: To get number of cases comparable to the number of controls, we multiplied the case numbers with the factor 1/0.157, as according to Morris et al⁴ we have only data from ∼15.7% of all Swiss aneuploidy cases in the considered time interval at our institution. For data preparation, we first removed for each postnatal case with aneuploidy a corresponding control–case in the reference data set, as in the latter all births (that is, including all cases with aneuploidies) were contained. It is important to note that this was performed for postnatal cases with trisomies 13, 18 and 21.

Results

The relation of maternal and paternal age of live births in the reference population

We determined the reference distribution of maternal and paternal ages in couples of 1 932 927 live births from Switzerland. To dissect the effect of younger and older fathers, we dichotomized our data in the study and reference data sets. To get an idea about the uncertainty in estimating proportions, we computed Wilson CIs at the Bonferroni-corrected level α*. The proportion of younger fathers (that is, group 2: m.≥f.) increases monotonically from 0.65% (Wilson CI: 0.5–0.8) in the mother's age group from 15 to 19 years, to 4.3% (4.2–4.5; 20–24 y.), 10.4% (10.3–10.5; 25–29 y.), 20.4% (20.2–20.5; 30–34 y.), 32.5% (32.2–32.8; 35–39 y.), 42.4% (41.7–43.1; 40–44 y.), 45.1% (41.8–48.5; 45–50 y.) and to 69.1% (54.9–80.5) in the mother's age group over 50 years (Table 1, Figures 2 and 3).

Table 1. Comparison of the parental ages from all childbearing married couples in Switzerland and from couples of the two independent study groups with a child with trisomy 13, 18 and 21.

			Trisomy 21			Postnatal (N=559)			Trisomy 13 and 18 (N=212)			Combine trisomies (N=969)
Mother's age group	Live births in Switzerland from 1979 to 2006 (N=1 932 226)		Prenatal (N=198)
	M.≥F.	M.<F.	M.≥F.	M.<F.	Odds ratio (99.4% CI)	M.≥F.	M.<F.	Odds ratio (99.4% CI)	M.≥F.	M.<F.	Odds ratio (99.4% CI)	M.≥F.	M.<F.	Odds ratio (99.4% CI)
10–14	0	0	0	0		0	1		0	0		0	1
15–19	106	16 270	0	0		1	7	21.9 (1.1–429.1) P 0.05	0	2	0.0 (0-NaN) P 1.00	1	9	17.1 (0.9–320.3) P 0.06
20–24	11 787	259 647	0	4	0.0 (0-NaN) P 1.00	6	43	3.1 (0.9–10.3) P 0.02	0	11	0.0 (0-NaN) P 1.00	6	58	2.3 (0.7–7.5) P 0.06
25–29	73 018	630 515	3	19	1.4 (0.2–7.6) P 0.49	20	100	1.7 (0.9–3.4) P 0.03	15	47	2.8 (1.2–6.3) P 0.001*	38	166	2.0 (1.2–3.3) P 0.0005*
30–34	132 643	518 743	7	24	1.1 (0.3–3.8) P 0.82	64	120	2.1 (1.4–3.2) P 0.00001*	12	47	1.0 (0.4–2.4) P 1.0	83	191	1.7 (1.2–2.4) P 0.0001*
35–39	80 795	167 745	28	48	1.2 (0.6–2.3) P 0.46	61	74	1.7 (1.1–2.8) P 0.002*	22	24	1.9 (0.8–4.3) P 0.04	111	146	1.6 (1.1–2.2) P 0.0004*
40–44	16 614	22 559	21	41	0.7 (0.3–1.5) P 0.20	32	17	2.6 (1.1–5.9) P 0.001*	19	9	2.9 (0.9–8.8) P 0.007	72	67	1.5 (0.9–2.3) P 0.03
45–49	762	928	1	2	0.6 (0.0–18.2) P 1.00	8	4	2.4 (0.4–13.4) P 0.16	3	1	3.7 (0.1–89.8) P 0.33	12	7	2.1 (0.6–7.9) P 0.16
50-	65	29	0	0		1	0		0	0		1	0

Comparison of the parental ages: in the first group the mother's age is at least as much as the fathers age (M.≥F.) and in the second group the father is older (M.<F.). Confidence intervals are indicated for the Bonferroni-corrected significance level α0=α/9=0.0056 (‘*' indicates significance after Bonferroni correction). Bold values indicate level of significance.

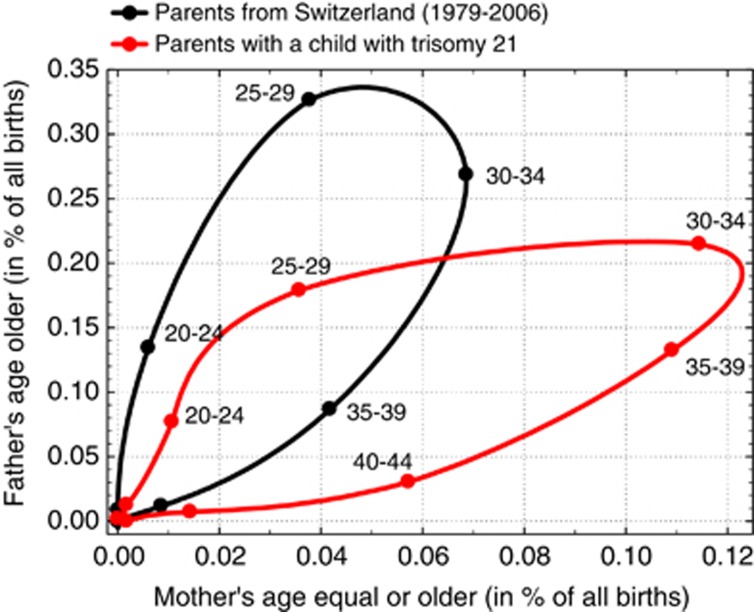
Figure 2.

Comparison of the parental ages in all married couples with live births in Switzerland in the years from 1979 to 2006 (N=1 932 927; black dots and line) and couples with a child with trisomy 21. Each point represents a maternal age group interval of 5 years. For each maternal age group the couples were dichotomized into two groups: in the first group the mother's age is equal or older than the father's age and in the second group the father is older.

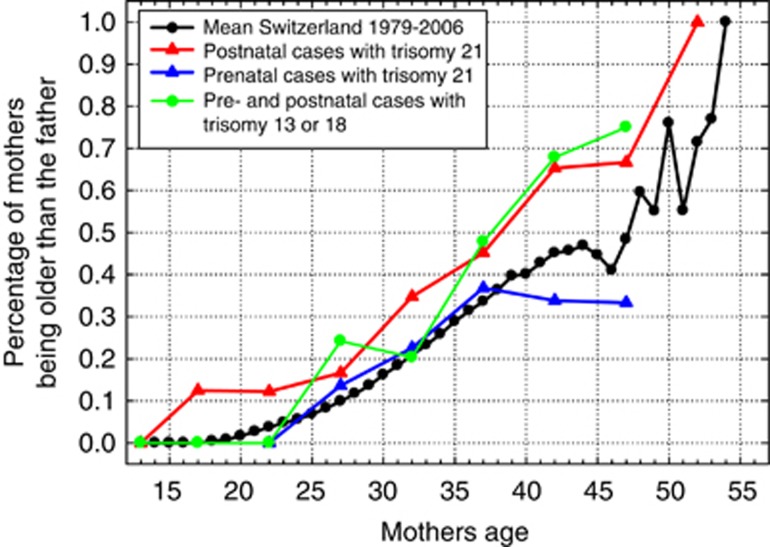
Figure 3.

Comparison of the parental ages in all married couples with live births in Switzerland in the years from 1979 to 2006 (N=1 932 927). The black dots represent one maternal year of age. The data from cases with trisomies 13, 18 or 21 are presented with colored symbols.

The relation of maternal and paternal ages in pre- and postnatal cases with DS

The proportion of younger fathers increased in both the prenatal and postnatal trisomy 21 group. In the postnatal trisomy 21 study group, the proportion rose continuously from 12.5% (Wilson CI: 1.3–60.4) in the mother's age group from 15 to 19 years, to 12.2% (4.3–30.5; 20–24 y.), 16.7% (9.3–28.0; 25–29 y.), 34.8% (25.8–45.0; 30–34 y.), 45.2% (33.9–57.0; 35–39 y.), 65.3% (45.6–80.9; 40–44 y.), 66.7% (30.0–90.3; 45–50 y.) and 100% (11.5–100) in the mother's age group over 50 years. In the group with prenatal trisomy 21 cases, this increase was less pronounced (0.0% (Wilson CI: 0.0–65.8; 20–24 y.), 13.6% (3.2–42.9; 25–29 y.), 22.6% (8.6–47.4; 30–34 y.), 36.8% (23.4–52.7; 35–39 y.), 33.9% (19.8–51.5; 40–44 y.), 33.3% (3.6–87.1; 45–50 y.). In some of the groups, the case numbers were critically low with high uncertainty in estimation of the proportions.

Comparison of parental ages between the reference and DS study group

In the study group with prenatal trisomy 21 cases in neither age group, a significant change of the risk for an offspring with aneuploidy was found. In the postnatal trisomy 21 cases the proportion of the group with younger fathers was significantly increased. The odds ratio for a child with trisomy 21 was elevated in all maternal age groups. Odds ratios were higher in the maternal age groups between 30 and 34 years: 2.1 (99.4% CI: 1.4–3.2; P 0.00001), between 35 and 39 years: 1.7 (99.4% CI: 1.1–2.8; P 0.002) and between 40 and 44 years: 2.6 (99.4% CI: 1.1–5.9; P 0.001). We only report age groups whose P-values are significant even after correction for multiple testing, that is, by comparison with the corrected significance level α*=α/9=0.0056.

Independent confirmation study and combined data sets

For confirmation of our findings in the primary DS study group we analyzed a second independent study group including pre- and postnatal cases with trisomies 13 and 18. In the combined group with cases with trisomies 13 and 18, the proportion of younger fathers increased continuously from 0.0% (Wilson CI: 0.0–79.4) in the mother's age group from 15 to 19 years, to 0% (0.0–41.1: 20–24 y.), 24.2% (12.5–41.5; 25–29 y.), 20.3% (9.7–37.8; 30–34 y.), 47.8% (29.2–67.0; 35–39 y.), 67.9% (42.0–86.0; 40–44 y.) and 75% (19.8–97.3) in the mother's age group 45–49 years. The odds for younger fathers were significantly higher in the maternal age groups from 25 to 29 years: 2.8 (99.4% CI: 1.2–6.3; P 0.001).

In the combined study group of the three aneuploidies, the proportion of younger fathers increased continuously from 10.0% (Wilson CI: 1.1–53.7) in the mother's age group from 15 to 19 years, to 9.4% (3.2–24.2: 20–24 y.), 18.6% (12.3–27.3; 25–29 y.), 30.3% (23.2–38.4; 30–34 y.), 43.2% (34.9–51.8; 35–39 y.), 51.8% (40.3–63.1; 40–44 y.) and 63.2% (33.2–85.5) in the mother's age group 45–49 years. The couples with younger fathers had higher odds in all maternal age groups: for 15–19 years: OR 17.1 (99.4% CI: 0.9–320.3; P 0.06), for 20–24 years: 2.3 (99.4% CI: 0.7–7.5; P 0.06), for 25–29 years: 2.0 (99.4% CI: 1.2–3.3; P 0.0005), for 30–34 years: 1.7 (99.4% CI: 1.2–2.4; P 0.0001), for 35–39 years: 1.6 (99.4% CI: 1.1–2.2; P 0.0004), for 40–44 years: 1.5 (99.4% CI: 0.9–2.3; P 0.03) and for 45–49 years: 2.1 (99.4% CI: 0.6–7.9; P 0.16). In the combined patients' group with the three most frequent postnatal autosomal aneuploidies, the couples with younger fathers were more likely to give birth to an affected offspring. This indicates a highly significant negative paternal age effect.

Regression analysis

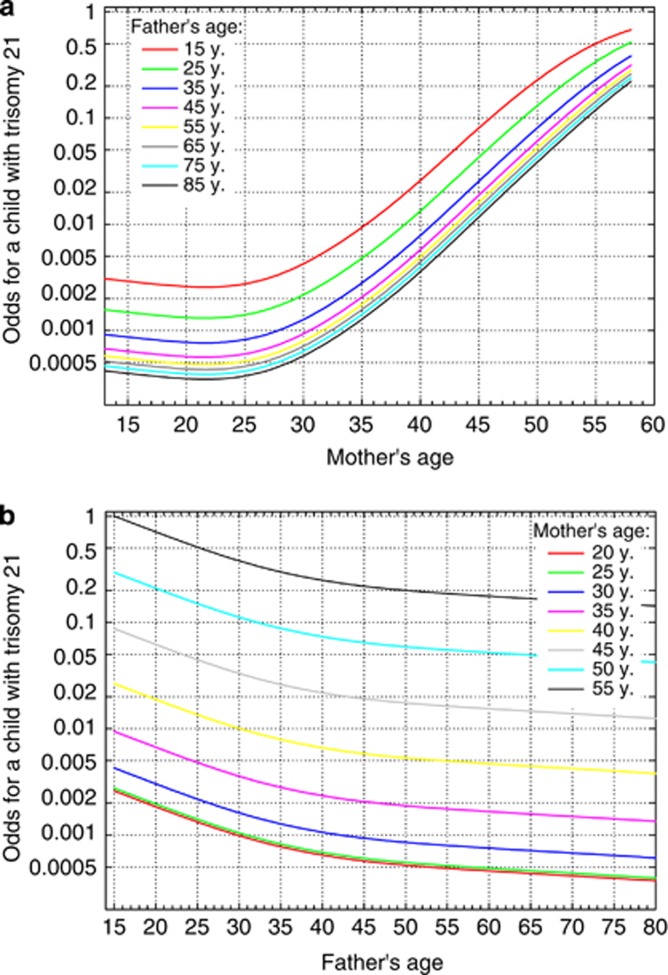
As a result of logistic regression with explanatory variables, mother's and father's age taken linearly into account, the odds for an offspring to be born with DS for a mother at the age of x+d were estimated to be by a factor exp(d · 0.1831) higher than for a mother at age x (see Table 2). These types of statements held true if the father's age was kept fixed. Specifically, per additional year of mother's age the odds for DS exponentially increased by the factor exp(0.1831)=1.20. For an increase in mother's age of d=10, we estimate an average increase in the odds for DS of exp(10 · 0.1831)=6.24. This interpretation held true for all age differences and for all maternal ages. The interpretation of the paternal age was similar. However, note that the sign for the estimated log odds was negative. This implies that the risk for DS decreased with increasing father's age. Specifically, for each additional year of age of the father, the odds for DS decreased by the factor exp(−0.0257)=0.97. The effect of the father's age was stronger in the model for the postnatal cases only, that is. the absolute value of the estimated coefficient was larger. Looking at the GAMs below and those with single smooth effects for mother's and father's age separately (not shown), it seemed that the effects of mother and father ages should not only be linearly modeled but at least quadratic. Table 3 provides a model that also includes quadratic effects and the models for pre- and postnatal cases are also given separately. The interpretation of the model with the quadratic effects is more complicated. The odds ratio does not only depend on the considered age difference d but also on the specific mother or father ages analyzed. More precisely, the odds for a father at age x+d compared with the odds at age x changed by a factor (for the mother's age left unchanged): g(x,d)=exp (−0.1985·d+0.0022 d(2x+d)). The interpretation for mother's age was similar. This phenomenon was also reflected in the estimated curves of predicted odds (Figure 4).

Table 2. Logistic regression models with all explanatory variables for pre- and postnatal cases with trisomy 21.

	Estimate	Estimated OR (exp(estimate))	95% Confidence interval	P-value
Pre- and postnatal DS cases
Intercept	−12.7040	<10−5	NA	<10−5
Mother	0.1831	1.20	1.18–1.22	<10−5
Father	−0.0257	0.97	0.96–0.99	0.002
Prenatal DS cases
Intercept	−18.6631	<10−5	NA	<10−5
Mother	0.282	1.33	1.28–1.37	<10−5
Father	0.0055	1.01	0.98–1.03	0.69
Postnatal DS cases
Intercept	−11.3900	<10−5	NA	<10−5
Mother	0.1485	1.16	1.13–1.19	<10−5
Father	−0.0392	0.96	0.94–0.98	0.0001

Table 3. Quadratic regression model with all explanatory variables for pre- and postnatal cases with trisomy 21.

	Estimate	Estimated OR (exp(estimate))	95% Confidence interval	P-value
Intercept	−3.7392	0.02	0.00–0.12	0.00001
Mother	−0.1694	0.84	0.77–0.93	0.00085
Mother 2	0.0053	1.005	1.004–1.007	<10−5
Father	−0.1985	0.82	0.76–0.89	<10−5
Father 2	0.0022	1.002	1.001–1.003	0.002

Figure 4.

Estimated age-specific live birth prevalence for Down syndrome. (a) Colored lines represent the estimated paternal age-specific odds for DS in relation to the maternal age. (b) Colored lines represent the estimated maternal age-specific odds for DS in relation to the paternal age.

GAM with joint function for explanatory variables

The resulting model was given in Figure 4. Note that in this figure, the contour lines were labeled with the log odds. The odds were generally increasing with increasing mother's age. As for the father's age we found that for fathers roughly older than 40, the probability for mothers to give birth to a child with DS was basically dependent on the mother's age only. For younger fathers, odds tended to decrease with increasing age (up to ∼40). Note that we did not include confidence bands in the plot (in order not to make it too confusing with too many lines, and since we inflated case numbers by 1/0.157) and that uncertainty is quite large for young and old fathers. As our DS study data set only involves ∼15.7% of all estimated postnatal DS cases (n=3561) in Switzerland between 1979 and 2006,⁴ we calculated risk estimates based on the estimated cases and the modeled relative risk from our data set.

Discussion

In our retrospective study, we analyzed mother's and father's age in live births from Switzerland during the years from 1979 to 2006. Using a large data set of this general reference population, we demonstrated a highly significant change of the parental age distribution by increasing mother's age. The paternal age had a highly significant effect on fertility and pregnancy outcome, as couples with a younger father had a higher probability of a successful live birth (from 0.65% for mother aged 15–19 years to 69.1% for mothers aged >50 years, see Table 1 and Huang² and de la Rochebrochard and Thonneau.³ In the primary DS study group the couples with younger fathers had more affected offspring with DS than their older counterparts in all maternal age groups, indicating a paternal age effect. A similar observation was recently reported for older mothers with fathers of age 20–24 years but not for paternal ages 25–29 years.²⁹ In all maternal age groups of our study, couples with younger fathers had nearly double the risk for a child with DS.

In general, we directly confirmed recent findings that reproductive success was reduced when both parents were advanced in age.³ By advancing maternal age, the proportion of childbearing females being older than their husbands was monotonically increasing, expressing a hidden paternal age effect. This ‘demographic' pattern was recognized in earlier studies and causes serious troubles for the statistical analysis of an etiological paternal age effect of paternal non-disjunction.¹⁵ When the wife's age was within the age groups having increased risk for DS, the fertility of the couple was the higher the younger the husband was. This independent ‘demographic' effect may have been counteracting a paternal age effect of paternal non-disjunction. As a consequence, it turned out to be difficult to detect any paternal age effect except a very strong one.^{15, 16, 17, 18, 19, 20, 21} Many studies had been designed to underline the etiological importance of paternal age for non-disjunction and have failed to detect any effect on the incidence of DS in addition to that accounted by the maternal age. Indeed, an independent paternal age effect was difficult to detect because of the high interactions between parental ages.

There are two hypothetically counteracting biological mechanisms we had to separate: on one hand, some studies showed a direct paternal age effect in fathers of advanced ages and, on the other hand, fertility was lower in these couples with older fathers. The simple dichotomization approach assisted to dissect the effect of older and younger fathers separately. As expected, the ‘demographic' paternal age effect was present in the reference population. The influence of the paternal age was outstanding and probably much larger than previously assumed. Most interestingly, the paternal effect was already present at young maternal ages and increased continuously. This steady increase in the general Swiss population was the baseline of the ‘demographic' paternal age effect.

In all maternal age intervals of the DS study group, a higher proportion of couples with younger husbands was present. This finding was confirmed in the independent study group with trisomies 13 and 18. The number of couples in the lower and upper ends of the age scale was limited. For the age groups with adequate numbers, the difference was highly significant, even after correction for multiple testing. These findings have also been explored by logistic regression models including parental ages as linear, quadratic and smooth functions via GAMs with joint function for both parental ages. The resulting models can be used to predict odds depending on parental ages, thereby quantifying the effect size. In the prenatal DS study group the negative paternal age effect was not significant and the ratio of older fathers significantly differed in prenatal cases at the 11th to 16th week of pregnancy compared with the ratio at birth. We therefore postulated a reduced chance of intrauterine survival for offspring with DS from older fathers. Age-dependent incidence figures both for the time of chorionic villus sampling, at amniocentesis and for newborns showed that about 17% of 21 trisomic fetuses die between the periods of CVS and amniocentesis and another 18% die between the time of amniocentesis and term.^{30, 31, 32} It is likely that these figures are even lower than the true incidences. If these corrections would be applied to the cases in our series, the figures likely would reach significance even for the prenatal cases. In cases with trisomies 13 and 18, the low numbers did not allow to differentiate between pre- and postnatal effects.

The increased relative risk for a child with DS in couples with younger fathers, with no consideration of the maternal age, has already been described by Roecker et al.³³ The different statistical methods used in their study also detected a strong negative paternal age effect, which supported the validity of our methods. A limitation of our study was that the study group was collected from only a part of the population from which the official data used for comparison were available. Indeed, the comparability of the two sets of data for this type of analysis was an important issue.¹⁵ To assess for sampling errors or statistical artifacts, we tested our hypothesis in an independent data set providing also evidence for an increased risk of aneuploidies of chromosomes 13 and 18 for younger fathers.

Our knowledge about the mechanisms underlying chromosomal non-disjunction in man is still surprisingly poor and only the advanced maternal age is a well-documented risk factor for non-disjunction. The increased risk for younger fathers is an unexpected finding, and the interpretation of this negative paternal age effect will give rise to different explanations. It is ahead of time to discuss possible interpretations of an association between the paternal age and an increased risk for a child with aneuploidy. Nevertheless, we postulate an independent negative paternal age effect that influences the couple's fertility. There is some biologic meaning, as the fertility of the couple is the higher the younger the husband is. Therefore, a higher risk for children with aneuploidies is not unexpected in couples with mothers of advanced age and young fathers. However, it is quite surprising that the paternal age has similar or even pronounced effects in mothers of young age, wherein chromosomal non-disjunction is rare and intrauterine survival is believed to be not significantly reduced. Our preliminary findings may have a major impact for decisions and procedures in artificial reproduction. For example, if a woman with the age of 35 years selects semen of a 20-year-old donor, this would indicate a nearly doubled risk for an offspring with aneuploidy compared with semen from a 40-years-ld male, for which, in contrast, the odds for dominant de novo mutations is increased. As a logical consequence, a systematic analysis of maternal and paternal ages in couples with children with genetic diseases due to dominant de novo mutations would be meaningful.

For a preliminary translation of our work into daily clinical work, we constructed estimated odds curves for both maternal and paternal ages. This preface plots need confirmation in further and larger independent studies. However, if replication of these findings can be achieved, the genetic and obstetric management of couples at risk needs a major correction of the risk stratification.

Unfortunately, molecular determination of the parental origin of the extra chromosome 21 could not be performed in our series. From examination of larger series of families with an index patient with free trisomy 21 (including about 200 patients from this series), it is known that in about 5–10% meiotic non-disjunction occurs in the sperm, and the age distribution of these families does not, in contrast to maternal meiotic failure, differ from normal controls.³⁴ Thus, it is unlikely that our sample would differ from that proportion, and that the results from our sample would be due to a higher incidence of paternal non-disjunction. A significant negative correlation between male age and hyperhaploidy in sperms was found in one study,³⁵ whereas several others found the contrary (see Buwe et al³⁶).

In addition, no determination of paternity could have been performed in this series. We therefore cannot exclude that in one or the other cases the legal father is not the biological father. However, it seems very unlikely that this could significantly modify the results. On the contrary, in these cases it is possibly more likely that the biological father would be younger than the legal father.

The authors declare no conflict of interest.