Skip to main content
. 2015 Dec 4;1(11):e1501057. doi: 10.1126/sciadv.1501057

Fig. 6. Example of how LSH groups fingerprints together in the database.

Fig. 6

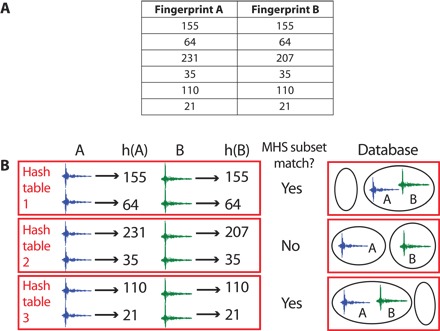
(A) Example of MHS for two similar fingerprints A and B, with p = 6. (B) LSH decides how to place two similar fingerprints A (blue) and B (green) into hash buckets (ovals) in each hash table (red boxes); waveforms are shown for easy visualization. The MHS length is p = 6, and there are b = 3 hash tables, so each hash table gets a different subset of the MHS of each fingerprint that is 6/3 = 2 integers long: the output of r = 2 Min-Hash functions. Taking each hash table separately: if the MHS subsets of A and B are equal, then A and B enter the same hash bucket in the database; this is true in hash tables 1 and 3, where h(A) = h(B) = [155, 64] and h(A) = h(B) = [110, 21], respectively. In hash table 2, however, the MHS subsets of A and B are not equal, because h(A) = [231, 35] and h(B) = [207, 35], so A and B enter different hash buckets.