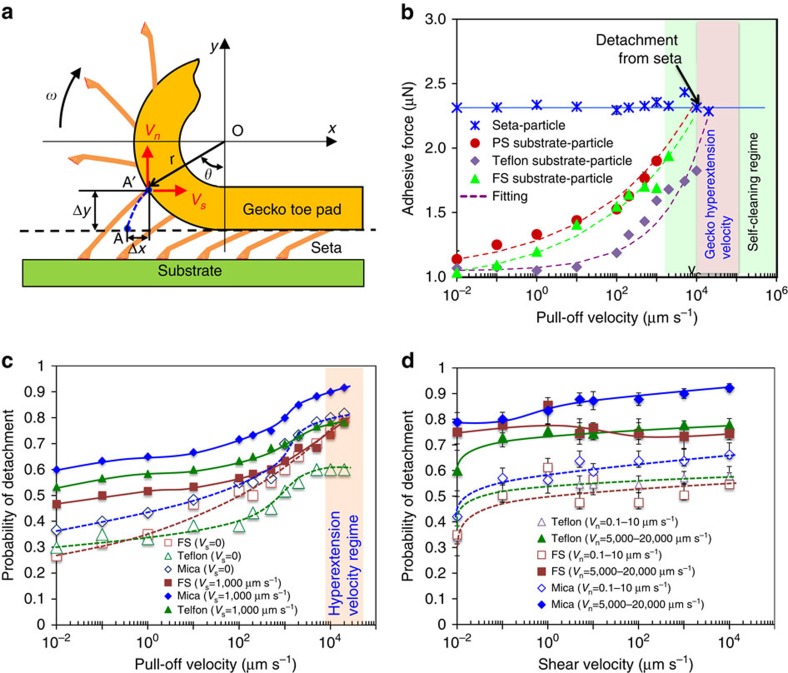
Figure 2. Gecko hyperextension and the probability of particle detachment from single setae.

(a) Schematic of gecko toe pad scrolling motion under digital hyperextension, which is modelled as a rolling motion of a circle, with a radius r, along a horizontal plane. The trajectory of a setal root (for example, from point A to A') follows the corresponding cycloid curve (for example, blue dashed line) depending on the specific location of each seta. The hyperextension generates normal velocity (V_n) as well as shear velocity (V_s) on the setal roots. (b) Dynamic adhesion responses between single seta and glass microsphere (F_s-p) and those between SiO₂ microparticles (d=10 μm) and FS, PS and teflon substrates (F_w-p) with increasing pull-off velocity (V_n). Probability of the SiO₂ particle (d=10–15 μm) detachment events from setae in 30-time trials on fused silica, mica and Teflon substrates as a function of (c) the pull-off velocity for shear velocities of 0, and 1,000 μm s⁻¹ and a preload of 1 μN, and (d) shear velocity at a preload of 1 μN for different pull-off velocities (error bar: s.d.). For the seta-particle contact experiments in (b), the microparticles are detached from the seta at 1,000–10,000 μm s⁻¹, depending on the type of substrates. These values are critical velocities V_c, above which the particles are detached from the setae. Note that the pull-off velocity of gecko setae during animal walking is estimated to be 10,000–30,000 μm s⁻¹, larger than the critical velocity V_c, suggesting that Tokay geckos' adhesive toe pads are always in the ‘self-cleaning regime' during animal locomotion. The estimated gecko pull-off velocity is illustrated in (b) and (c).