Fig. 1.

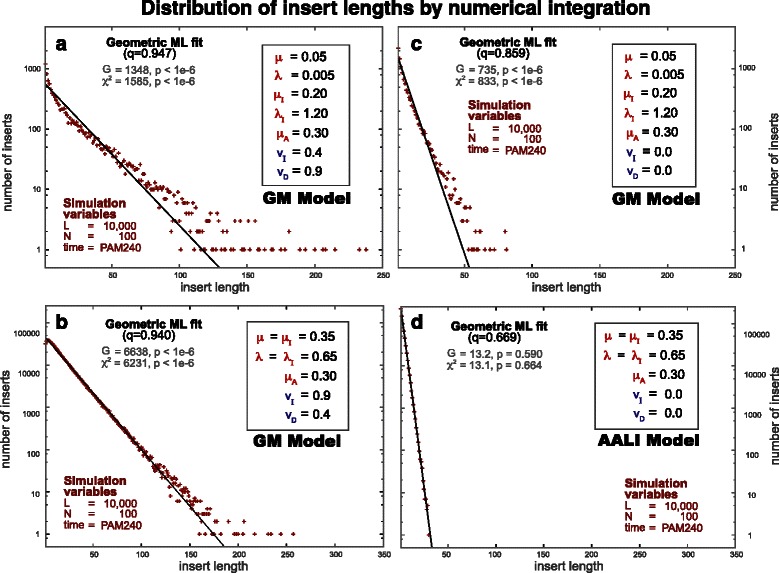
Under the GM evolutionary model, the length of inserts does not follow in general a geometric distribution, and therefore this model is incompatible with affine gap cost alignment. A sample of N=100 ancestral sequences of length L = 10,000 are evolved according to the GM model to different divergence times. The y-axis is given in logarithmic scale, thus a geometric distribution becomes a straight line. At a given divergence time t, evolved sequences are obtained by sampling from the infinitesimal time microscopic model at discrete intervals of δ t=10⁻⁵. For the particular divergence time corresponding to PAM240 (t=2.2), we present the histogram of insert lengths (i.e. the number of residues between any two ancestral positions) for several sets of parameter values. The black line corresponds to a maximum likelihood fit of the data to a geometric distribution of the form q ^l(1−q) with its corresponding G and χ ² goodness-of-fit tests and their corresponding probabilities. Panels (a) and (b) both consider cases in which residues are added according to geometric distributions. In particular, panel (b) considers that case in which λ=λ _I and μ=μ _I. In panels (c) and (d) all geometric parameters are zero, and residues are added one at a time. The particular parameters in Panel (d) corresponds to the AALI evolutionary model, a special case of the GM model in which insert length fits a geometric distribution. Notice that a straight line (geometric fit) is not sufficient to demonstrate affine models, because linear models (like the AALI model) also produce geometric insert lengths