Fig. 11.

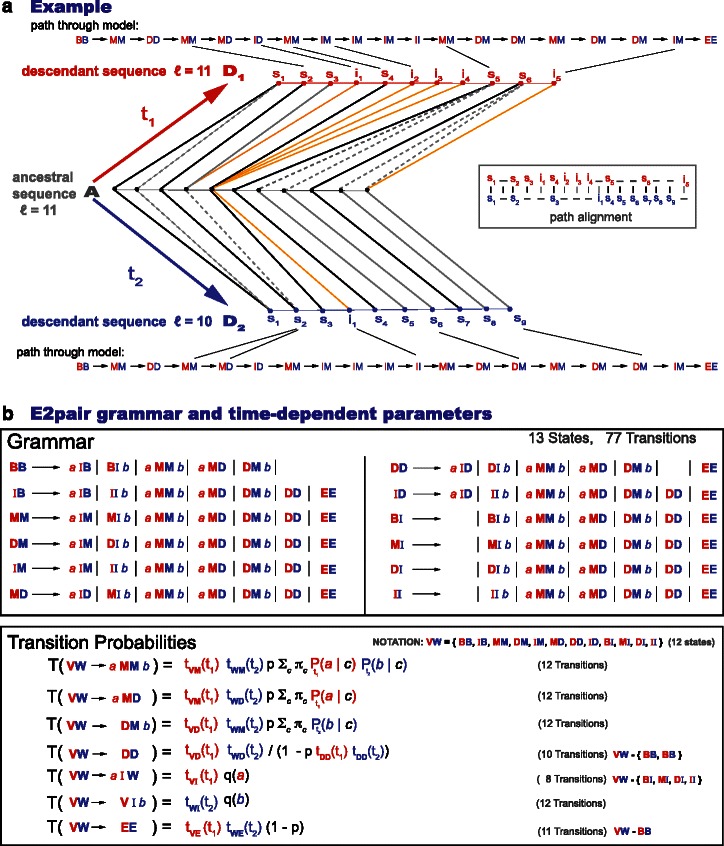
Model for aligning two extant sequences related by a common ancestor using an affine gap-cost and generally not reversible evolutionary model. a In the example, two extant sequences (marked with red and blue) are aligned according to an evolutionary history that involves an ancestral sequence of 11 residues, 5 aligned positions, one double deletion, and 11 gaps. Some of the gaps correspond to ancestral residues deleted in either of the sequences, and some of the gaps correspond to insertions (relative to the ancestor) in one of the two extant sequences. Many different choices of ancestral sequence and evolutionary histories (in addition to this example) contribute to that particular alignment. The E2pair model describes the probability associated to each of those processes. b The E2pair model grammar is described here. A particular history can be derived in only one way by the grammar (an unambiguous grammar). Since the ancestral sequence is an unknown, the model sums over all possible ones. The transition probabilities t_VW(t) are given by one of the evolutionary models specified in Table 1 evolutionary model (see also Fig. 2 and Fig. 3). The emission probabilities include a time-dependent substitution matrix P _t(a∣b), a residue distribution for emitting inserted residues q _I(a), and another one for ancestral residues π(a). There is also the geometric parameter p describing the distribution of ancestral sequence lengths. Since double deletions are not observed, the algorithm also sums over all of them. The factor 1/(1−pt_DDt_DD) that appears in all the transitions into the DD state, corresponds to summing over all possible DD→DD…→DD transitions, given by $\sum _{n=1}^{\infty }{\left(p{\mathrm{t}}_{\text{DD}}{\mathrm{t}}_{\text{DD}}\right)}^n$