Fig. 3.

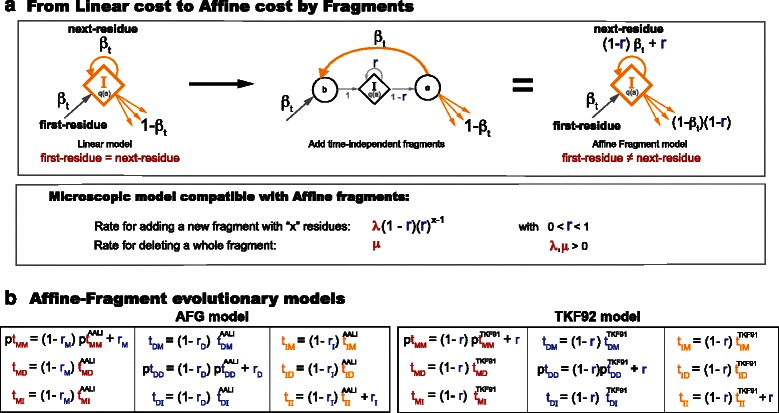
Affine fragment evolutionary models. a It is possible to convert a linear-cost model into an affine-cost one by adding units of indivisible “fragments”, each having a geometrically-distributed length. The resulting macroscopic affine model is compatible with a microscopic evolutionary model in which groups of residues are added/removed together instantaneously with a length controlled by a time-independent geometric Bernoulli parameter, with the condition that groups of residues created instantaneously together have to also die together. b Macroscopic fragments can be added to any state with a self-loop transition. The AFG model (Table 1) is a fragment derivative of the AALI model. In the TKF92 model (a fragment derivative of TKF91) fragments are added to all three M/D/I states with the same parameter r. The AFG model becomes reversible in the particular case that it uses the transition probabilities of the LR model, and by setting the Insert and Delete fragment parameters equal to each other (r _I=r _D). We call the reversible version of the AFG model the affine fragment reversible (AFR) model