Figure 3.

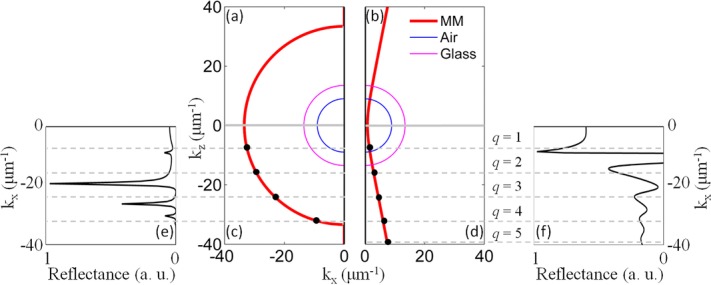
(a) and (b) Isofrequency contours in the first Brillouin zone calculated for a frequency corresponding to a free-space wavelength λ₀ = 700 nm for an infinite Au nanorod metamaterial with p = 0.5 for (a) ordinary, TE, and (b) extraordinary, TM, modes. In the elliptic regime (a), the dispersion is bounded and corresponds to that of a typical anisotropic dielectric. The isofrequencies contours in the superstrate (air) and the substrate (glass) are also shown. (c) and (d) The mode position of a metamaterial slab (400 nm in thickness) shown as dots corresponding to intersection of the isofrequency contours of the infinite metamaterial with the quantized values of k_z = q(π/l), where q = ±1, ±2, ±3,… resulting from the finite size of the slab in the z-direction. (e) and (f) Angular spectra of reflectance of the metamaterial slab as in (c) and (d) for λ₀ = 700 nm calculated using TMM. The position of the modes obtained analytically is shifted to higher wavevectors due to the analytic model assumptions, influencing the confinement of the modes.