Fig. 1.

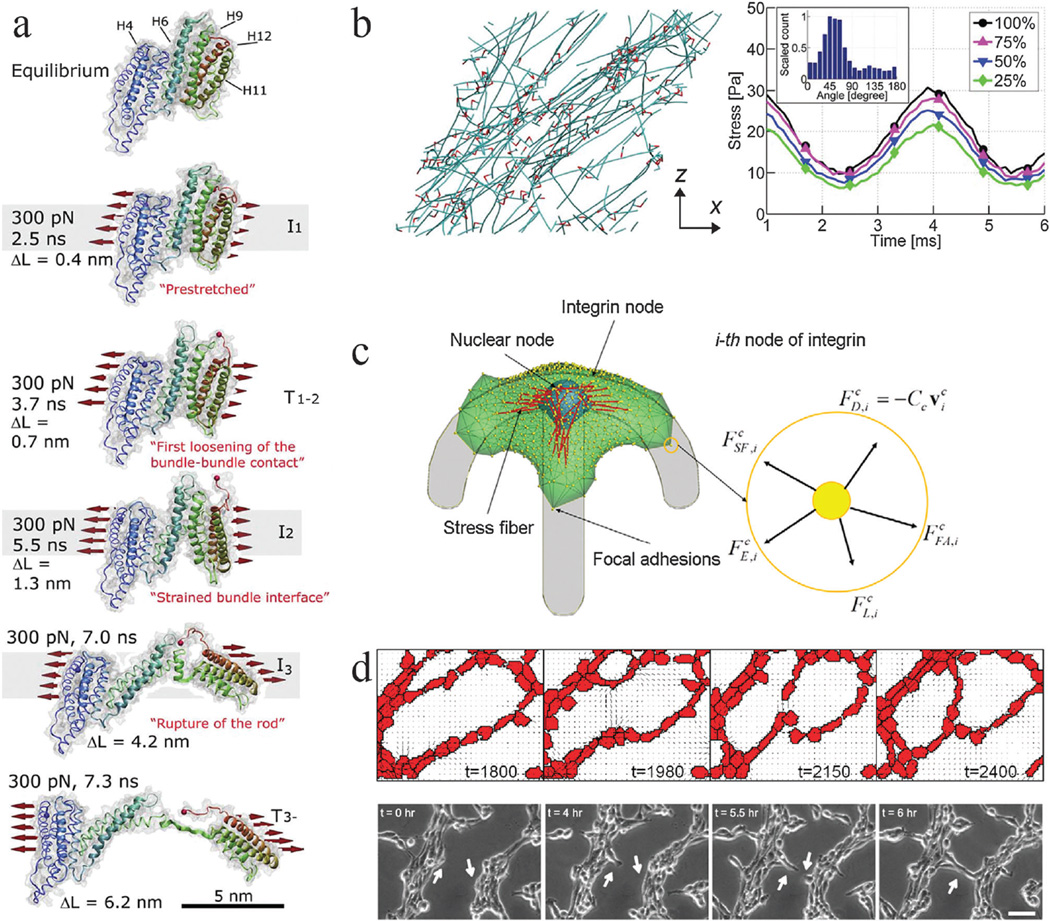
Mechanobiology simulations from molecular to multicellular scales. Coarse graining of simulation elements or reduction in system interactions is required to simulate larger scales due to computational cost. (a) Steered molecular dynamics simulation of a stretching force applied to the H1–H12 rod of talin, adapted from ref. 2. Talin has five vinculin binding helices (H4, H6, H9, H11, H12) in its rod domain. As the molecule is stretched by a 300 pN force distributed across its cross section (as indicated), the amount of buried surface area of the vinculin binding sites is reduced, suggesting increased binding affinity for vinculin. ΔL corresponds to the increase in length of the domain as compared to its equilibrium length, which is 3.2 nm. (b) Brownian dynamics simulations of actin (teal) networks connected via actin crosslinking proteins ACPs (red), adapted from ref. 4. (left) A prestrain is applied to this network in the x direction, inducing stress on ACPs and actin. This model predicts that a supportive framework emerges in this network that bears the majority of the stress, such that removal of large fractions of ACPs and actin still enables most of the stress to be sustained when identical oscillatory strain is applied (right). Simulation results provide insights that different mechanisms, such as ACP and actin bending and extension, dictate network viscoelasticity depending on prestrain. (c) A single-cell migration model with focal adhesions, stress fibers, protrusions, and a nucleus, adapted from ref. 110. The cell can adhere to a micropatterned surface and generate spatial profiles of traction forces comparable to experimental studies. Focal adhesions adhere to the substrate and stress fibers can connect to adhesion sites and the nucleus. 3D force balance calculations are performed at each integrin node. This model provides a platform for investigating how prominent intracellular components interact with each other and respond to environmental constraints to generate an integrated cell response. It also implicates the nucleus as a cause for asymmetry in leading and trailing edge adhesion dynamics. (d) Hybrid Potts and finite element model of endothelial networks, adapted from ref. 13. (top) Endothelial cells generate forces and deform a soft substrate. Neighboring cells respond to substrate strains and undergo durotaxis, leading to the formation of networks from single cells that resemble experimental observations (bottom). This model provides indications of how force signals can lead to endothelial morphogenesis.