Abstract
Whether or not chiral interaction exists between the optical orbital angular momentum (OAM) and a chiral molecule remains unanswered. So far, such an interaction has not been observed experimentally. Here we present a T-matrix method to study the interaction between optical OAM and the chiral molecule in a cluster of nanoparticles. We find that strong interaction between the chiral molecule and OAM can be induced by the excitation of plasmon resonances. An experimental scheme to observe such an interaction has been proposed. Furthermore, we have found that the signal of the OAM dichroism can be either positive or negative, depending on the spatial positions of nanocomposites in the cross-sections of OAM beams. The cancellation between positive and negative signals in the spatial average can explain why the interaction has not been observed in former experiments.
Many biomolecules are chiral in nature. Chirality plays a pivotal role in biochemistry and the evolution of life itself1,2. When chiral molecules interact with circularly polarized photons, they exhibit optical activity, such as the circular dichroism (CD) effect describing the difference in molecular absorption of right- and left-handed circularly polarized photons. The related CD spectroscopic technique has been one of the central methods for optically probing the molecular chirality3,4. In addition to polarized light, which is intrinsically linked to the spin angular momentum of photons, photons can carry orbital angular momentum (OAM), which is associated with the helicity in spatial phase distribution5,6,7,8,9,10. Over the past decades, many researchers have studied the interactions between OAM photons and chiral molecules11,12,13,14,15,16,17,18. Although many of them have predicted an exchange can occur between the OAM of the photon and the center of mass motion of the molecule, whether OAM photons can interact with molecular chirality remains an open question.
Vortex beams with various OAMs have been experimentally realized in the optical domain5,6. The possibility of encoding large amounts of information in vortex beams due to the absence of an upper limit has raised the prospects of their applicability in information processing tasks7,8. The OAM beams have been widely used in manipulating and trapping microscopic particles9,10. The problem is whether vortex beams with OAMs can be used to probe molecular chirality? Does this additional degree of freedom play a role in CD? If the interaction between the OAM and the chiral molecule was found, it is potentially useful for a broad range of research areas and applications. Thus, the electromagnetic (EM) interactions of OAM photons with atoms and molecules have received considerable attention11,12,13,14,15,16,17,18. Some theoretical investigations predicted that the interaction of OAM light with atoms and molecules should be observable within the electric dipole approximation11,12,13, but the others obtained a contradictory result14,15,16. The latter outcome has been supported by recent experimental studies17,18, which verified that the influence of the OAM on CD of chiral molecules can not be detectable.
On the other hand, recent investigations have demonstrated that light-molecule interactions can be enhanced via resonant excitations of surface plasmon resonance (SPR) of metallic nanostructures. For CD probe of molecular chirality, it has been reported a large difference in absorption of right- and left-handed circularly polarized photons in the SPRs19,20,21,22,23,24,25,26,27. In addition, the SPRs have been also used to improve nanoparticle(NP)-assisted biosensing28,29,30 and Raman scattering31,32,33. In this work, we attempt to explore the role of SPRs in the promotion of the interactions between the OAMs and the chiral molecules.
To address this issue, we study the interaction between the OAM beams and the nanocomposite comprising chiral molecule and metallic NPs. A method to study such an interaction has been developed by using the T-matrix. Based on such a method, we study the interaction between OAM beams and chiral molecules located in the vicinity of NPs. We find that the strong interaction between the chiral molecule and OAM can be induced by the excitation of plasmon resonances of NPs. Experimentally, such an interaction could be observed if we define the OAM dichroism (OD) to be the difference of absorption rates between two focused linear polarized OAM beams with opposite topological indices. We should stress here that a nonzero spatial-average OD signal exists only for the nanocomposites located in a certain spatial region of OAM beams. In addition, we also find that the OD can be further enhanced when the orientations of nanocomposites are fixed.
Results and Discussions
We consider here a semi-classical hybrid system consisting of a molecules and a cluster of 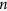 NPs, which is excited by an OAM beam with
NPs, which is excited by an OAM beam with 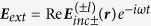 and
and 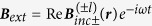 ,
, 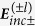 and
and 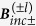 represent electronic and magnetic fields of the OAM beam (their expressions in aplanatic system are given in supplementary materials). The intensity of the incident wave is considered to be weak enough that the mechanical interaction between the light and the hybrid system can be neglected. The molecules used here are assumed to be point-like two-level systems, no vibrational structure of transitions is considered. According to the previous investigations, the master equation for quantum states of the molecule can be written as19,23,25
represent electronic and magnetic fields of the OAM beam (their expressions in aplanatic system are given in supplementary materials). The intensity of the incident wave is considered to be weak enough that the mechanical interaction between the light and the hybrid system can be neglected. The molecules used here are assumed to be point-like two-level systems, no vibrational structure of transitions is considered. According to the previous investigations, the master equation for quantum states of the molecule can be written as19,23,25
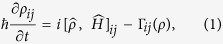 |
where 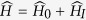 is the Hamiltonian of the molecule and
is the Hamiltonian of the molecule and 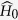 describes the internal electronic structure of the molecule,
describes the internal electronic structure of the molecule, 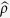 is the density matrix and
is the density matrix and 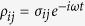 is the corresponding matrix element. Here
is the corresponding matrix element. Here 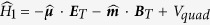 is the light-matter interaction operator,
is the light-matter interaction operator, 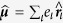 and
and 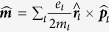 are electric and magnetic operators, and
are electric and magnetic operators, and 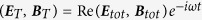 represents the EM field acting on the molecule. Where
represents the EM field acting on the molecule. Where 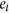 ,
, 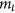 ,
, 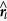 and
and 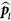 are the electric charge, mass, position and momentum operators for the
are the electric charge, mass, position and momentum operators for the 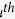 charged particle in the molecule system. The electric quadrupole interaction term
charged particle in the molecule system. The electric quadrupole interaction term 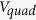 bears the same order of magnitude with the magnetic dipole term
bears the same order of magnitude with the magnetic dipole term 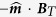 , whose expression is written as
, whose expression is written as 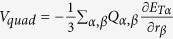 , with
, with 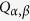 being the element of the electric quadrupole operator. In this work we set the electric dipole of the molecule to be aligned with the rotational symmetry axis of the nano system. Thus, this term makes no contribution to the dichroism and can be omitted here.
being the element of the electric quadrupole operator. In this work we set the electric dipole of the molecule to be aligned with the rotational symmetry axis of the nano system. Thus, this term makes no contribution to the dichroism and can be omitted here. 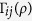 is the relaxation term which describes the damping with
is the relaxation term which describes the damping with 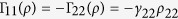 ,
, 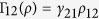 and
and 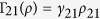 . By solving this equation within rotating-wave approximation, and letting
. By solving this equation within rotating-wave approximation, and letting 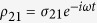 , we can obtain energy absorption rate of the system:
, we can obtain energy absorption rate of the system:
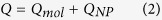 |
where 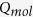 represents the absorption rate of the molecule in the system, which is expressed as
represents the absorption rate of the molecule in the system, which is expressed as
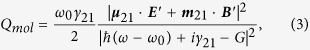 |
where 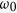 is the frequency of molecular transition,
is the frequency of molecular transition, 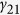 is the relaxation term,
is the relaxation term, 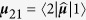 and
and 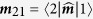 are the matrix elements of electric and magnetic dipole momentum operators.
are the matrix elements of electric and magnetic dipole momentum operators. 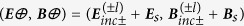 , with
, with 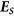 and
and 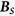 being the EM field of scattered wave by the NPs in the absence of the molecule.
being the EM field of scattered wave by the NPs in the absence of the molecule. 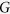 is the function which describes the broadening of the resonance peak of the signal due to the interactions between the molecules and NPs, and its expression can be founded in ref. 25. The induced dipole of the molecule is given by
is the function which describes the broadening of the resonance peak of the signal due to the interactions between the molecules and NPs, and its expression can be founded in ref. 25. The induced dipole of the molecule is given by 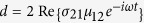 .
. 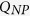 in Eq. (2) is the absorption rate of NPs in the system. According to the law of energy conservation, it equals to the energy flows into them. Thus we have
in Eq. (2) is the absorption rate of NPs in the system. According to the law of energy conservation, it equals to the energy flows into them. Thus we have
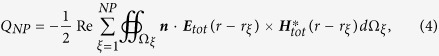 |
where 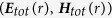 are the amplitudes of the total complex EM field in the space, and
are the amplitudes of the total complex EM field in the space, and 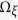 denotes a surface circumscribing around the
denotes a surface circumscribing around the 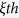 NP. If we define OAM dichroism (OD) of the system as the difference of absorption rate between two focused linear polarized OAM beams with opposite topological indices
NP. If we define OAM dichroism (OD) of the system as the difference of absorption rate between two focused linear polarized OAM beams with opposite topological indices 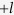 and
and 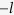 , at the same time, they are space inversion of each other, it can be expressed as
, at the same time, they are space inversion of each other, it can be expressed as
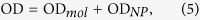 |
where 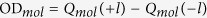 represents the contribution of the molecule in the molecule-NP nanocomposites, whose value is influenced by the NPs.
represents the contribution of the molecule in the molecule-NP nanocomposites, whose value is influenced by the NPs. 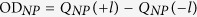 is the molecule-induced OD for the nanoparticles, where
is the molecule-induced OD for the nanoparticles, where 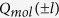 and
and 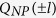 can be written as (see methods section for detail)
can be written as (see methods section for detail)
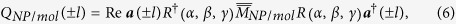 |
where 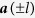 is arranged as
is arranged as 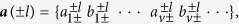 with
with 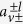 and
and 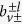 are set to be the vector spherical function (VSF) expansion coefficients of an OAM beam propagating along the
are set to be the vector spherical function (VSF) expansion coefficients of an OAM beam propagating along the 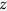 direction (see supplementary material).
direction (see supplementary material). 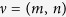 is introduced here for notation simplification, and the convention
is introduced here for notation simplification, and the convention 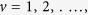 when
when 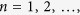 and
and 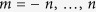 is used. Absorption of waves in any direction can be calculated by changing the Euler angles
is used. Absorption of waves in any direction can be calculated by changing the Euler angles 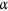 ,
, 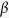 and
and 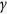 .
. 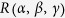 is the rotation matrix which depends only on the direction of the incident wave which is given in refs 34, 35, 36, while
is the rotation matrix which depends only on the direction of the incident wave which is given in refs 34, 35, 36, while 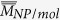 is a matrix determined only by the property of the illuminated system, which has the form of
is a matrix determined only by the property of the illuminated system, which has the form of
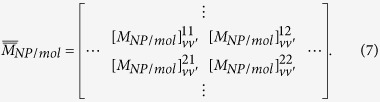 |
Based on Eqs. (4, we can obtain OD through numerical calculations. However, the results depend on geometrical configuration of the system. For example, the OD signals for the NP-molecule system being fixed in a certain region in space but possessing random orientations are different from those for the case being distributed uniformly in the whole space with random orientations. They are also different from the case, which the direction of the chiral system is fixed, and the system is distributed uniformly in some certain regions. In the following, we will deal with each case separately.
OD for nanocomposites with fixed positions and random orientations
In practice, molecule-NP nanocomposites in liquid environment have random orientations, averaging over the solid angles of the directions of the samples need to be done. This is equivalent with averaging over the solid angles of the directions of the incident light as has been considered for the calculation of absorption and CD spectra19,23,25,26. Likewise, we did the average OD calculations for a system with random orientations but fixed position. The absorption for the OAM light by nanoparticles and the molecule should be rewritten as
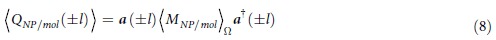 |
with
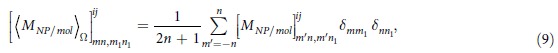 |
where 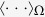 represents the averaging over the solid angle. For a chiral system,
represents the averaging over the solid angle. For a chiral system, 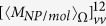 or
or 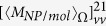 should not be vanished. Also by analyzing the properties of
should not be vanished. Also by analyzing the properties of 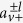 and
and 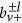 under space inversion, the orientation averaged OD of the system is given by (see methods section for detail)
under space inversion, the orientation averaged OD of the system is given by (see methods section for detail)
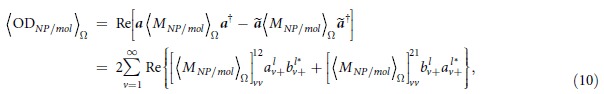 |
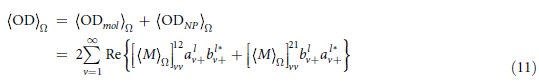 |
with 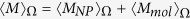 . From the above equations, the orientation averaged OD of the system can be obtained.
. From the above equations, the orientation averaged OD of the system can be obtained.
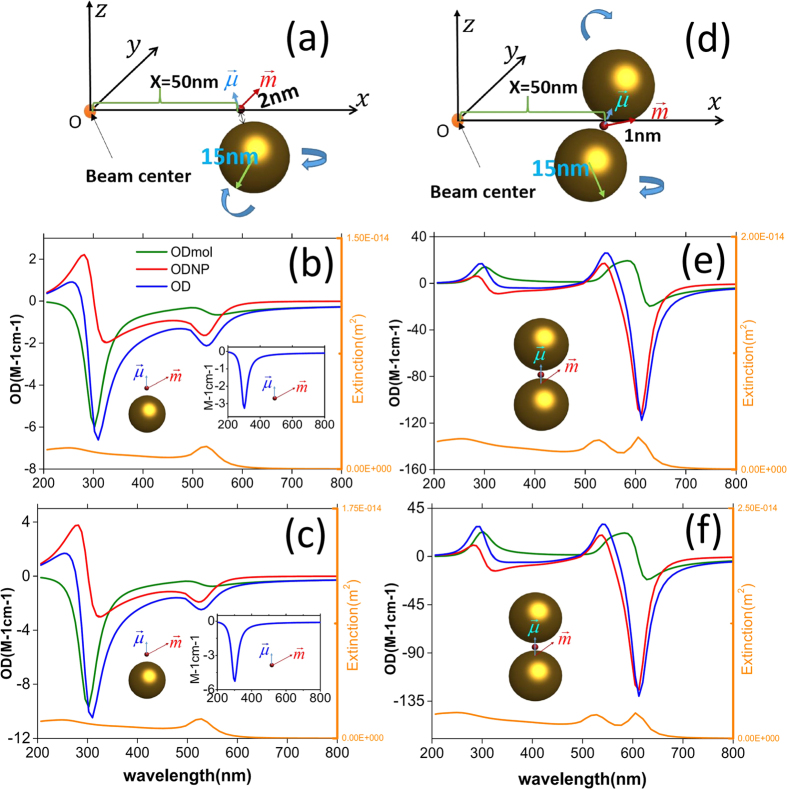
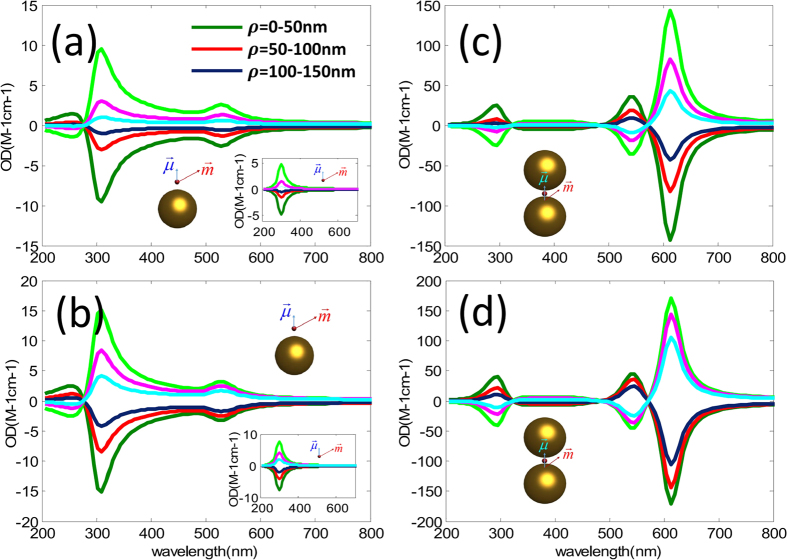
Figure 1(b,c) show the calculated orientation averaged OD as a function of wavelength for a chiral molecule being placed in the vicinity of a single gold sphere (Fig. 1(a)) for the OAM incident beam with 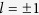 and
and 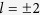 , respectively. Here the OAM beams used are x directional polarized Laguerre-Gaussian (LG) lights with a numerical aperture of
, respectively. Here the OAM beams used are x directional polarized Laguerre-Gaussian (LG) lights with a numerical aperture of 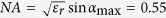 and having a filling factor of
and having a filling factor of 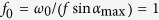 . The focusing position of the beam locates at the origin of the coordinate, as shown in Fig. 1(a). The radius of the gold sphere is taken as 15 nm, the distance between the chiral molecular and the sphere is taken as 2 nm. The parameters of the molecular dipole are taken according to refs. 1 and 23:
. The focusing position of the beam locates at the origin of the coordinate, as shown in Fig. 1(a). The radius of the gold sphere is taken as 15 nm, the distance between the chiral molecular and the sphere is taken as 2 nm. The parameters of the molecular dipole are taken according to refs. 1 and 23: 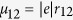 and
and 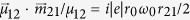 with a resonance wavelength of 300 nm. The direction of the electric dipole of the molecule is set to be align with the symmetry axis of the NP. In our calculations, we use
with a resonance wavelength of 300 nm. The direction of the electric dipole of the molecule is set to be align with the symmetry axis of the NP. In our calculations, we use 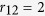 Å,
Å, 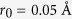 and
and 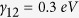 . For the dielectric functions of Au, the Johnson’s data were adopted37, the permittivity of water is taken to be
. For the dielectric functions of Au, the Johnson’s data were adopted37, the permittivity of water is taken to be 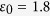 . If the OD signals are in units of
. If the OD signals are in units of 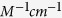 , they have to be multiplied by
, they have to be multiplied by 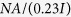 where
where 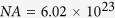 is Avogadro’s number19,23, I is related to the square of the incident electric field through
is Avogadro’s number19,23, I is related to the square of the incident electric field through 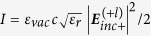 .
.
Figure 1.
(a) System of coordinates and schematics of a complex composed of a gold nanoparticle and chiral molecule. (b,c) Orientation averaged OD as a function of wavelength for a metal nanoparticle and chiral molecule under the OAM incident beam with 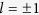 and
and 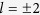 , respectively. The insets represent the calculated results for the single chiral molecule without NPs. (d) System of coordinates and schematics of a NP dimer and a chiral molecule. (e,f) Calculated OD as a function of wavelengths for the Au dimer and a chiral molecule under the OAM incident beam with
, respectively. The insets represent the calculated results for the single chiral molecule without NPs. (d) System of coordinates and schematics of a NP dimer and a chiral molecule. (e,f) Calculated OD as a function of wavelengths for the Au dimer and a chiral molecule under the OAM incident beam with 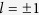 and
and 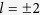 , respectively. Calculated extinctions for the corresponding systems are also shown. The radius of NPs are taken 15 nm and the separation between two NPs is 1 nm.
, respectively. Calculated extinctions for the corresponding systems are also shown. The radius of NPs are taken 15 nm and the separation between two NPs is 1 nm.
The green line and red line in Fig. 1 correspond to 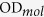 and
and 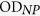 , respectively, the total OD is described by the blue line. The extinction cross section of the gold sphere is plotted as the orange line, and the plasmon resonance peak appears at the wavelength of 520 nm. Comparing the present OD spectra with that of pure chiral molecular (without the NP, insets of Fig. 1(b,c)), we find that the
, respectively, the total OD is described by the blue line. The extinction cross section of the gold sphere is plotted as the orange line, and the plasmon resonance peak appears at the wavelength of 520 nm. Comparing the present OD spectra with that of pure chiral molecular (without the NP, insets of Fig. 1(b,c)), we find that the 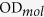 signal around
signal around 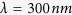 is improved about 2 times. Moreover, a new OD band appears in the plasmon resonance spectral region. These results reveal not only a plasmon-enhanced chiral molecule-OAM interaction at the molecule resonance frequency, but also an OD effect at the plasmonic resonant frequency of metallic NP. Note that spherical NP itself is achiral, such an induced plasmonic OD correlated with the enhanced interaction between the chiral molecular and the OAM has not been reported in previous studies.
is improved about 2 times. Moreover, a new OD band appears in the plasmon resonance spectral region. These results reveal not only a plasmon-enhanced chiral molecule-OAM interaction at the molecule resonance frequency, but also an OD effect at the plasmonic resonant frequency of metallic NP. Note that spherical NP itself is achiral, such an induced plasmonic OD correlated with the enhanced interaction between the chiral molecular and the OAM has not been reported in previous studies.
For a single sphere, the enhancement of OD signal by the NP is small and weak. When the chiral molecule is put in the hotspot of the dimer, as shown in Fig. 1(d), giant enhancement effect can be observed. The cases when the molecule is put in the gap of an Au dimer with an inter particle distance of 1nm is presented in Fig. 1(e,f) for the OAM beam with 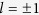 and
and 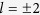 , respectively. Comparing it with the case of the single sphere, the total
, respectively. Comparing it with the case of the single sphere, the total 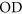 is significantly enhanced near the wavelength of coupled plasmon resonance. Specifically, the plasmonic
is significantly enhanced near the wavelength of coupled plasmon resonance. Specifically, the plasmonic 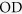 at the hotspot can be 50 times larger than that of the single sphere when
at the hotspot can be 50 times larger than that of the single sphere when 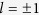 , while the enhancement of
, while the enhancement of 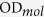 can also reach 30 times. The phenomena are similar for the OAM beam with different topological indices such as
can also reach 30 times. The phenomena are similar for the OAM beam with different topological indices such as 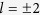 illustrated in Fig. 1(f).
illustrated in Fig. 1(f).
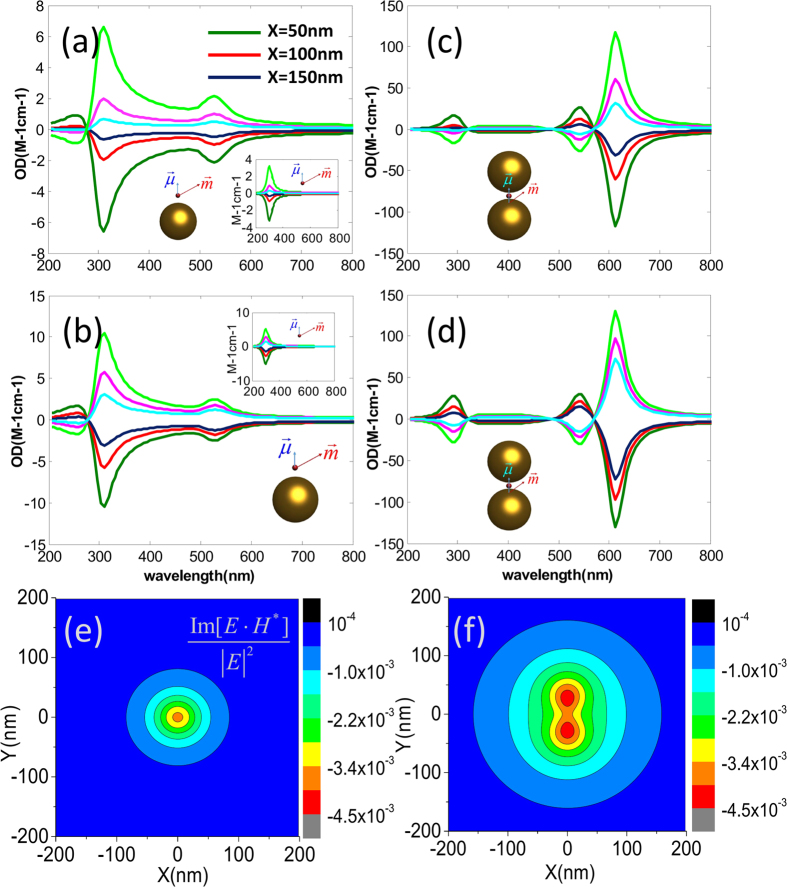
Considering that the EM field of the OAM beam is nonuniform in space, we investigate the OD signal at different position of the OAM beams. Figure 2(a,b) correspond to the case of single sphere with 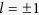 and
and 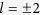 , respectively, Fig. 2(c,d) to the case of dimer. The olive/red/black blue line in Fig. 2 represents the orientation averaged OD when the molecule is put at x = 50 nm/100 nm/150 nm in the focal plane (origin of the coordinate is set to be the focal center of the OAM beams). The corresponding OD for the mirror reflected samples are also plotted as green, pink and sky blue lines, as expected these signals are of same values but opposite signs. With the position of the nanocomposite is shifted away from the beam center, the OD signal decreases. In order to disclose such a phenomenon we rewrite Eq. (10) under the dipole approximation, which means the cut-off of
, respectively, Fig. 2(c,d) to the case of dimer. The olive/red/black blue line in Fig. 2 represents the orientation averaged OD when the molecule is put at x = 50 nm/100 nm/150 nm in the focal plane (origin of the coordinate is set to be the focal center of the OAM beams). The corresponding OD for the mirror reflected samples are also plotted as green, pink and sky blue lines, as expected these signals are of same values but opposite signs. With the position of the nanocomposite is shifted away from the beam center, the OD signal decreases. In order to disclose such a phenomenon we rewrite Eq. (10) under the dipole approximation, which means the cut-off of 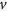 is set to be 1. If we consider the nanocomposite system being located not too close to the beam center, the electric and magnetic fields illuminated on it can be viewed as a constant vector. Using Eqs.(8) and (11), and expand the incident wave according to Eqs. (42, 43), the OD can be rewritten as
is set to be 1. If we consider the nanocomposite system being located not too close to the beam center, the electric and magnetic fields illuminated on it can be viewed as a constant vector. Using Eqs.(8) and (11), and expand the incident wave according to Eqs. (42, 43), the OD can be rewritten as
Figure 2.
Orientation averaged OD as a function of wavelength under the OAM incident beam when the nanocomposites locate at 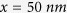 (olive line),
(olive line), 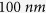 (red line) and
(red line) and 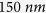 (blue dark line), respectively. The corresponding signals for the mirror reflected system are presented as green (
(blue dark line), respectively. The corresponding signals for the mirror reflected system are presented as green (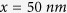 ), pink (
), pink (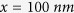 ), blue (
), blue (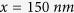 ). (a,b) correspond to the system of a metal nanoparticle and chiral molecule with
). (a,b) correspond to the system of a metal nanoparticle and chiral molecule with 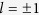 and
and 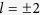 , respectively. (c,d) to the system of a NP dimer and a chiral molecule with
, respectively. (c,d) to the system of a NP dimer and a chiral molecule with 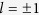 and
and 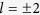 , respectively. (e,f) describe
, respectively. (e,f) describe 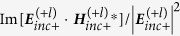 as a function of position for the incident OAM beam with
as a function of position for the incident OAM beam with 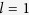 and
and 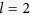 at the wavelength of 300 nm, respectively.
at the wavelength of 300 nm, respectively.
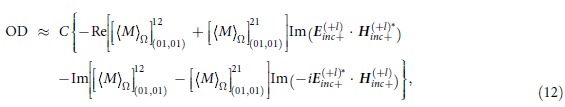 |
where  is a real constant. It is worth to note when the molecule is put inside the gap of the dimer, Eq. (12) is still valid if
is a real constant. It is worth to note when the molecule is put inside the gap of the dimer, Eq. (12) is still valid if 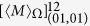 and
and 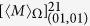 are solved beyond the dipole approximation (see methods section for detail). Our calculations show that the first term in Eq. (12) plays a leading role in the OD signals, thus the signal is proportional to
are solved beyond the dipole approximation (see methods section for detail). Our calculations show that the first term in Eq. (12) plays a leading role in the OD signals, thus the signal is proportional to 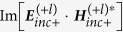 . This variable has been firstly introduced by Tang and Cohen to characterize the chirality of light38, since they are proportional to the difference of absorption rates between two oppositely handed molecules. Later it was Cameron et al.39 who indicated that this term is in fact proportional to the helicity density which describes the ‘screw action’ of the EM field40. The calculated results for
. This variable has been firstly introduced by Tang and Cohen to characterize the chirality of light38, since they are proportional to the difference of absorption rates between two oppositely handed molecules. Later it was Cameron et al.39 who indicated that this term is in fact proportional to the helicity density which describes the ‘screw action’ of the EM field40. The calculated results for 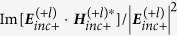 as a function of position are plotted in Fig. 2(e,f) for the OAM beam with
as a function of position are plotted in Fig. 2(e,f) for the OAM beam with 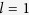 and
and 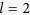 at the wavelength of 300 nm, respectively. It can be found the value of
at the wavelength of 300 nm, respectively. It can be found the value of 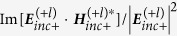 is close to that of the circular polarized wave, of which value decreases with the increase of the relative distance between nanocomposites and the center of the beam, which directly leads to the decrease of the OD signal. This phenomenon has also been reported in ref. 41, where a large helicity density has been observed at the center of the Bessel beam with the OAM.
is close to that of the circular polarized wave, of which value decreases with the increase of the relative distance between nanocomposites and the center of the beam, which directly leads to the decrease of the OD signal. This phenomenon has also been reported in ref. 41, where a large helicity density has been observed at the center of the Bessel beam with the OAM.
We would like to point out that the above OD signals originate from the interaction of the OAM and the chiral molecule, which are not because of the spin angular momentum, because we have used the linear polarized OAM light as the incident wave with no spin angular moment even when it is strongly focused by lens42,43.
The previous theoretical investigations have shown that only the spin angular momentum leads to a differential absorption, there is no interaction of the OAM of the beam with the chirality of the molecule14,15,44,45. This is because the signals calculated in these works are the average of contributions from all the molecules in spaces. In fact, our calculated results have also shown that the OD signals do not exist in the case of the whole spatial average either, which will be discussed in the following section.
OD for nanocomposites with whole spatial average
Because of heterogeneity of the OAM beam in space, the spatial average for the OAM dichroism is needed in some cases, for example, to compare the theoretical results with the experimental measurements as described in refs. 18,19. Here we consider a spatial averaged OD performed in the focal plane normal to the propagation direction of the OAM beam, which can be expressed as
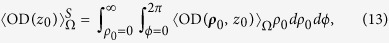 |
where 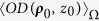 is the angular averaged OD signal of the system which is located at
is the angular averaged OD signal of the system which is located at 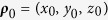 . Substituting Eq. (10) into Eq. (13), we find
. Substituting Eq. (10) into Eq. (13), we find
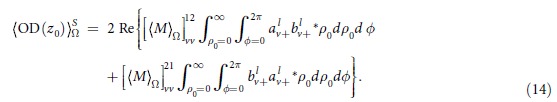 |
The involved integration in Eq. (14) can be calculated analytically by using the integrations given in (supplementary materials). If we use  and
and 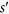 to stand for
to stand for 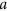 and
and 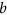 , the involved integration in Eq. (14) can be expressed as
, the involved integration in Eq. (14) can be expressed as
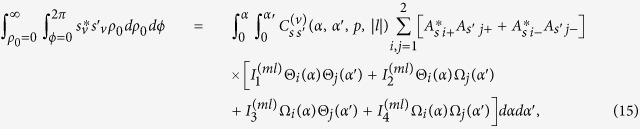 |
with
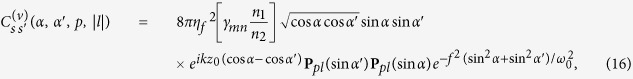 |
where 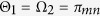 and
and 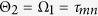 . The terms
. The terms 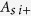 ,
, 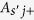 ,
, 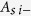 and
and 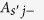 are polarization dependent coefficients, their expressions are written as
are polarization dependent coefficients, their expressions are written as
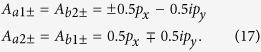 |
The expressions for 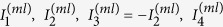 and the meaning for all the involved variables have been given in supplementary materials. Substitute Eq. (14) into Eq. (12), using the condition
and the meaning for all the involved variables have been given in supplementary materials. Substitute Eq. (14) into Eq. (12), using the condition 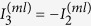 , it can be founded that
, it can be founded that 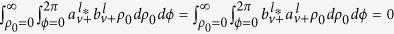 for linear polarized beams (
for linear polarized beams (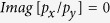 ). Thus from Eq. (14), we can see that
). Thus from Eq. (14), we can see that 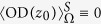 for any linear polarized OAM beam.
for any linear polarized OAM beam.
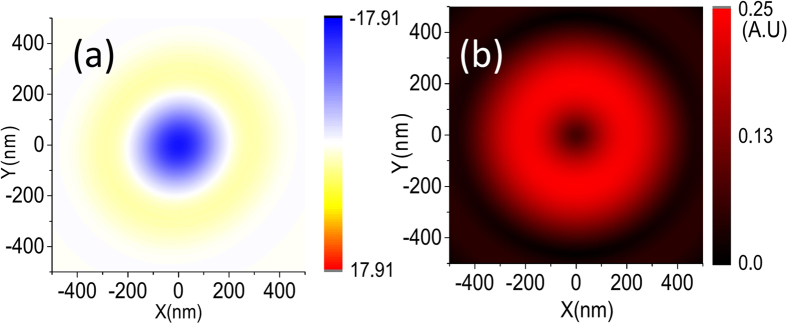
In order to analyze the physical origin of the phenomenon, we plotted in Fig. 3(a) the 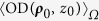 distribution in the focal plane at the wavelength of 300 nm for the molecule-NP system described in Fig. 1(a). The X-polarized OAM beam with
distribution in the focal plane at the wavelength of 300 nm for the molecule-NP system described in Fig. 1(a). The X-polarized OAM beam with 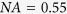 and
and 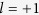 is used. The corresponding intensity distribution of the incident electric field is plotted in Fig. 3(b) for comparison. One can see that the OD signal of this molecule-NP system change sign when it is moved away from the beam center. The cancellation between positive and negative signals in the spatial average explains why
is used. The corresponding intensity distribution of the incident electric field is plotted in Fig. 3(b) for comparison. One can see that the OD signal of this molecule-NP system change sign when it is moved away from the beam center. The cancellation between positive and negative signals in the spatial average explains why 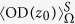 is zero. Here it is worth to note that even though the electric field intensity in the central region is weak, the OD signal in this region is still large due to the higher helicity density near the beam center.
is zero. Here it is worth to note that even though the electric field intensity in the central region is weak, the OD signal in this region is still large due to the higher helicity density near the beam center.
Figure 3.
(a) The OD distribution in the focal plane at the wavelength of 300 nm for the molecule-NP system described in Fig. 1a. The OAM beams have 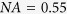 and
and 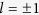 . (b) The corresponding intensity distribution of the electric field at the wavelength of 300 nm.
. (b) The corresponding intensity distribution of the electric field at the wavelength of 300 nm.
In fact, from the above theory, the same conclusion can be drawn for the single molecule without NPs. This may explain why the influence of the OAM on the CD of chiral molecules has not been observed in the previous experiments17,18. Our theory has demonstrated that the OD signal from the chiral molecule can not be observed in the whole spatial average even with the aid of plasmonic NPs. It is worth to note that 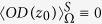 is also true for systems of pure NPs since Eq. (10) is valid in the absence of the molecule. Thus such an OD signal can not be observed for the structural chirality25,46,47,48,49,50,51,52,53. Although the OD signal does not exist due to the whole spatial average, we can still observe the signal at some conditions. In the following, we will discuss such phenomena.
is also true for systems of pure NPs since Eq. (10) is valid in the absence of the molecule. Thus such an OD signal can not be observed for the structural chirality25,46,47,48,49,50,51,52,53. Although the OD signal does not exist due to the whole spatial average, we can still observe the signal at some conditions. In the following, we will discuss such phenomena.
OD for nanocomposites with fixed orientations in a defined region
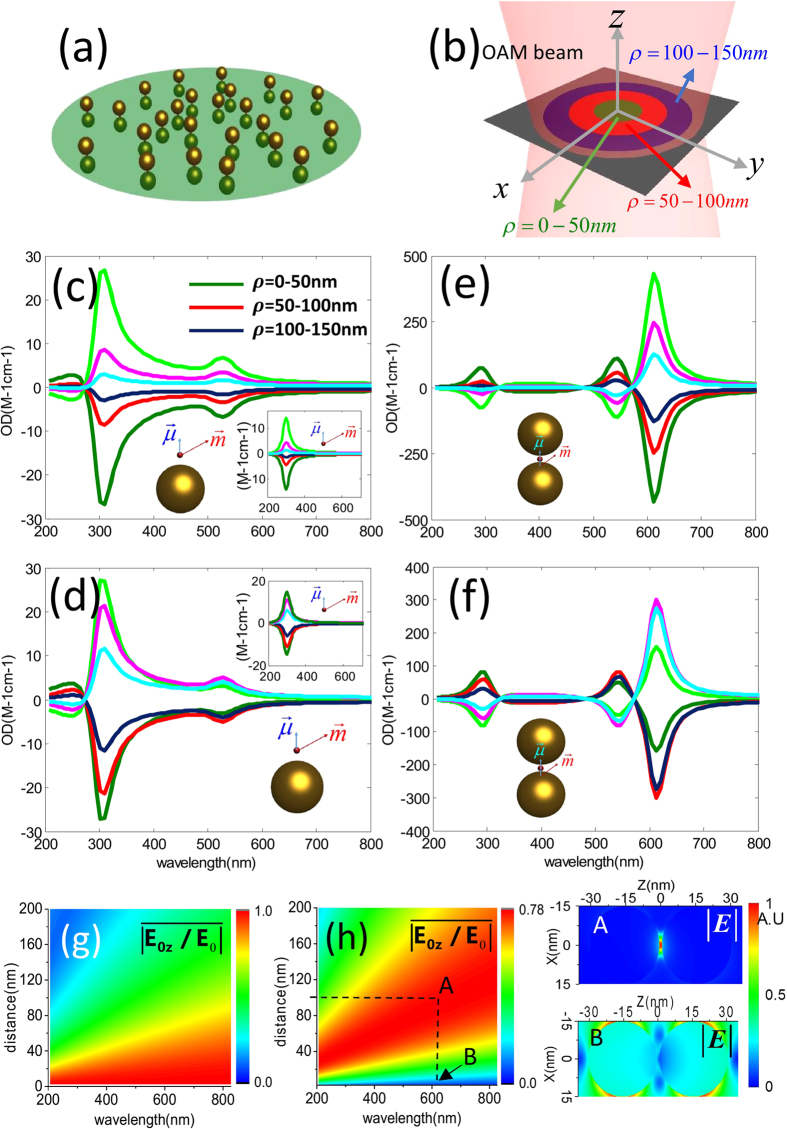
We consider some NPs locate in some defined regions, as shown in Fig. 4(a). The samples are concentrated in some circular areas. In these areas, the samples have fixed axis relative to the incident waves. In a real experiment, this corresponds to the situation where the molecules or the composite systems are fixed on the substrate. Here the direction of the molecule’s electric dipole is set to be aligning with the incident OAM wave and the symmetry axis of the composite system. If the incident wave is oblique, the OD signal appears even when the structure is achiral. This effect also occurs for circular polarized waves known as extrinsic dichroism caused by mutual orientations of incident waves and samples54,55,56. In the following, we consider the cases where the OD signals are gathered from circular areas around the beam center under the vertical incidence (see Fig. 4(b)). Specifically the OD signal is rewritten as
Figure 4.
(a) The distribution of nanocomposites with fixed orientations in a circular region. (b) Schematics of the OAM beam and the regions being considered. The green region marks = 0–50 nm, red region corresponds to ρ = 50–100 nm, blue region to ρ = 100–150 nm. (c,d) Orientation fixed OD averaged in some regions as a function of wavelengths for a metal nanoparticle and a chiral molecule under the OAM incident beam with 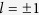 and
and 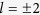 , respectively. The insets represent the corresponding results for the single chiral molecule without NPs. (e,f) Orientation fixed OD averaged in some regions as a function of wavelengths for the Au dimer and a chiral molecule under the OAM incident beam with
, respectively. The insets represent the corresponding results for the single chiral molecule without NPs. (e,f) Orientation fixed OD averaged in some regions as a function of wavelengths for the Au dimer and a chiral molecule under the OAM incident beam with 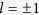 and
and 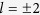 , respectively. The olive/red/dark blue lines correspond to the signals in
, respectively. The olive/red/dark blue lines correspond to the signals in  = 0–50 nm/
= 0–50 nm/ = 50–100 nm/
= 50–100 nm/ = 100–150 nm regions. The corresponding signals for the mirror reflected system are presented as green/pink/blue lines. (g,h) Averaged relative values of the longitude electric field magnitude as a function of the relative distances between the center of the x-polarized OAM beam and nanocomposites for the case with
= 100–150 nm regions. The corresponding signals for the mirror reflected system are presented as green/pink/blue lines. (g,h) Averaged relative values of the longitude electric field magnitude as a function of the relative distances between the center of the x-polarized OAM beam and nanocomposites for the case with 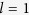 and
and 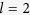 , respectively. Panel A: electric field distribution for a dimmer when the molecule is put at
, respectively. Panel A: electric field distribution for a dimmer when the molecule is put at 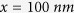 in the focal plane; Panel B: electric field distribution for a dimmer when the molecule is put at the center of the beam. The other parameters are taken identical with those in Fig. 1.
in the focal plane; Panel B: electric field distribution for a dimmer when the molecule is put at the center of the beam. The other parameters are taken identical with those in Fig. 1.
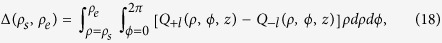 |
When setting  and
and 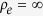 , Eq. (18) also gives the result for the whole spatial average, it is
, Eq. (18) also gives the result for the whole spatial average, it is 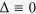 for all the cases (single molecule or molecule-NP systems), which is the same with the orientation averaged case discussed above. However, if the spatial average is calculated for some defined regions, the situation becomes different. The olive, red and dark blue lines in Fig. 4 are the calculated results for the orientation fixed OD that are averaged in some spatial regions as shown in Fig. 4(b), which correspond to the region
for all the cases (single molecule or molecule-NP systems), which is the same with the orientation averaged case discussed above. However, if the spatial average is calculated for some defined regions, the situation becomes different. The olive, red and dark blue lines in Fig. 4 are the calculated results for the orientation fixed OD that are averaged in some spatial regions as shown in Fig. 4(b), which correspond to the region 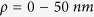 ,
, 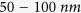 and
and 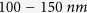 , respectively. The corresponding OD for the samples with opposite chirality are shown by green, pink and sky blue lines. The results are calculated from Eq. (18) numerically, and multiplied by a factor of
, respectively. The corresponding OD for the samples with opposite chirality are shown by green, pink and sky blue lines. The results are calculated from Eq. (18) numerically, and multiplied by a factor of 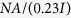 for normalization. Here
for normalization. Here 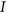 is equal to
is equal to 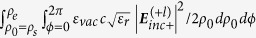 .
.
Figure 4(c,d) show the calculated results for the nanocomposite consisting of an Au nanoparticle and a chiral molecule under the OAM incident beam with 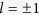 and
and 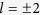 , respectively, while (e,f) are for the system with Au dimer and a chiral molecule. The parameters of nanocomposites are taken identical with those in Fig. 1. The corresponding OD signals for the single molecule without NPs are plotted in the insets of Fig. 4(c,d). In contrast to the case under the whole spatial average, we find that strong plasmon-induced OD signals appear for the region spatial average. Generally they decrease with the increase of the relative distances between nanocomposites and the center of the beam, that is, the maximum appears in the region
, respectively, while (e,f) are for the system with Au dimer and a chiral molecule. The parameters of nanocomposites are taken identical with those in Fig. 1. The corresponding OD signals for the single molecule without NPs are plotted in the insets of Fig. 4(c,d). In contrast to the case under the whole spatial average, we find that strong plasmon-induced OD signals appear for the region spatial average. Generally they decrease with the increase of the relative distances between nanocomposites and the center of the beam, that is, the maximum appears in the region 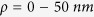 . However, it is different for the case in Fig. 4(f) for the dimer system with
. However, it is different for the case in Fig. 4(f) for the dimer system with 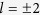 , the maximum of OD signals appear in the region
, the maximum of OD signals appear in the region 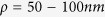 . This is because the relative value of the longitude part of the electric field
. This is because the relative value of the longitude part of the electric field 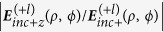 at various wavelengths has different behaviors for the OAM incident beam with
at various wavelengths has different behaviors for the OAM incident beam with 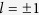 and
and 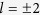 .
.
In Fig. 4(g,h), we plot the value of 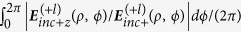 at the focal plane as a function of the wavelength and the relative distances between the center of the x-polarized OAM beam and nanocomposites for the case with
at the focal plane as a function of the wavelength and the relative distances between the center of the x-polarized OAM beam and nanocomposites for the case with 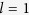 and
and 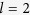 , respectively. The relative values of the longitude electric field in the region
, respectively. The relative values of the longitude electric field in the region 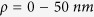 is obviously larger than those in other regions for the case with
is obviously larger than those in other regions for the case with 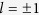 . This is in contrast to the case with
. This is in contrast to the case with 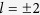 , where the maximum of the longitude electric field appears in the region
, where the maximum of the longitude electric field appears in the region 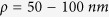 . The magnitude of the longitude electric field determines the field intensity in the hotspots of the dimer. In panels A and B of Fig. 4, we plot the intensity distribution of the electric field in the dimer under the OAM incident beam with
. The magnitude of the longitude electric field determines the field intensity in the hotspots of the dimer. In panels A and B of Fig. 4, we plot the intensity distribution of the electric field in the dimer under the OAM incident beam with 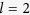 at the wavelength of 605 nm. Panel A corresponds to the case where the dimer is put at
at the wavelength of 605 nm. Panel A corresponds to the case where the dimer is put at 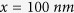 , while Panel B is for the same system situated at the center of the beam. Since the OAM beam with
, while Panel B is for the same system situated at the center of the beam. Since the OAM beam with 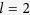 has a vanishing
has a vanishing 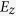 at the center of the beam57, no hotspot is generated. This means that the electric field is not greatly amplified in the position of the molecule.
at the center of the beam57, no hotspot is generated. This means that the electric field is not greatly amplified in the position of the molecule.
The calculated results shown in Fig. 4 are only for the case under the spatial average in some defined regions when the orientations of nanocomposites are fixed. In fact, if we consider random orientations of nanocomposites and do orientation average for such a case again, the OD signals still exist. Figure 5 displays the calculated results. The results in Fig. 5(a–d) correspond to those in Fig. 4(c–f), respectively. Comparing them, we find that the OD signals decrease when the orientation averages are performed, however, plasmon-induced OD signals are still large.
Figure 5.
(a,b) Orientation averaged OD in some regions as a function of wavelength for a metal nanoparticle and chiral molecule under the OAM incident beam with 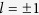 and
and 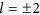 , respectively. The insets represent the corresponding results for the single chiral molecule without NPs. (c,d) Orientation averaged OD in some regions as a function of wavelength for the Au dimer and a chiral molecule under the OAM incident beam with
, respectively. The insets represent the corresponding results for the single chiral molecule without NPs. (c,d) Orientation averaged OD in some regions as a function of wavelength for the Au dimer and a chiral molecule under the OAM incident beam with 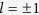 and
and 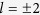 , respectively. The olive/red/dark blue lines correspond to the signals in
, respectively. The olive/red/dark blue lines correspond to the signals in  = 0–50 nm/
= 0–50 nm/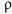 = 50–100 nm/
= 50–100 nm/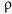 = 100–150 nm regions. The corresponding signals for the mirror reflected system are presented as green/pink/blue lines.
= 100–150 nm regions. The corresponding signals for the mirror reflected system are presented as green/pink/blue lines.
Conclusions
In summary, we have developed a T-matrix method to study the interaction between optical OAM and the chiral molecule in a cluster of nanoparticles. Our results have revealed that the strong interaction between the chiral molecule and OAM can be induced by the excitation of plasmon resonances. Such an interaction leads to the OAM dichroism effect, which depends on the geometrical configuration of the molecule-NP system, such as the orientations and spatial positions of nanocomposites, in the illumination of OAM beam. It is important to note that the sign of the OAM dichroism signal can be either positive or negative, depending on the spatial positions of the nanocomposite in the cross-section of OAM beams. In this point, experimental observation of a nonzero OAM dichroism signal from the molecule-NP system is challenging, since it requires spatial arrangement of nanocomposites in a very limited space region of the incident OAM beam. This leads to the OAM wave improper for the detection of the chirality of samples which are randomly distributed. However, it does not prevent the OAM beam from becoming as an alternative probe of the chirality of an individual nano structure. Since the OAM adds another dimension for the judgment of the chirality of nano structure in addition to the spin angular momentum, we believe it may play an important role in the realization and improvement of chirality detection at the nanoscale55,58. Our theoretical study reveals here the possibility to observe the interactions between chiral molecules and OAM beams, which paves the way to explore a novel plasmon-based spectroscopic technique for optically detecting the molecular chirality.
Methods
T-matrix formula for the absorption rate
In this section, we provide the T-matrix formula for the absorption rate. The incident wave can be expanded as a series of VSFs in a coordinate system of which origin is set to the position of the molecule:
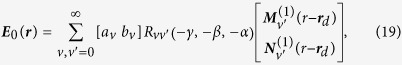 |
where 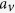 and
and 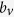 are the expansion coefficients of the incident wave propagating along the
are the expansion coefficients of the incident wave propagating along the 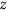 direction,
direction, 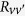 is the 2 × 2 rotation block matrix, which is related to two sets of VSFs by the following relation
is the 2 × 2 rotation block matrix, which is related to two sets of VSFs by the following relation
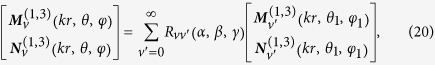 |
where 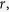
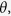
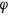 and
and 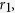
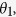
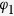 are the spherical coordinates of the same evaluated point in the coordinate system
are the spherical coordinates of the same evaluated point in the coordinate system  and
and  , respectively. The coordinate system
, respectively. The coordinate system  is obtained from the
is obtained from the  through the Euler rotation
through the Euler rotation 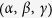 . The EM field
. The EM field 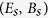 scattered by NPs in the absence of the molecule, are related to the incident wave by the T-Matrix, and they can be expressed as
scattered by NPs in the absence of the molecule, are related to the incident wave by the T-Matrix, and they can be expressed as
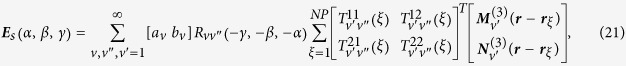 |
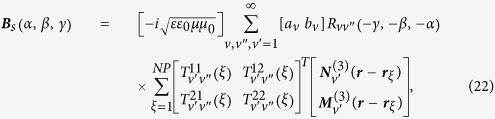 |
where  (
(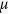 ) and
) and 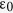 (
(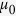 ) are the relative and absolute permittivity (permeability) in the space and vacuum, respectively.
) are the relative and absolute permittivity (permeability) in the space and vacuum, respectively. 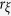 is the coordinate of the
is the coordinate of the 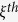 sphere,
sphere, 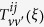 are elements of the coupled T-matrix (
are elements of the coupled T-matrix (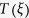 ) of the
) of the 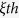 NP, and they are related to the general single particle T-Matrix
NP, and they are related to the general single particle T-Matrix 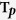 by the following equations:
by the following equations:
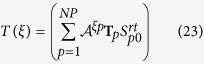 |
with 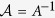 , and the block-matrix components of
, and the block-matrix components of 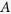 are written as
are written as 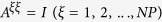 and
and 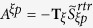 (
(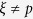 ). Here
). Here 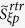 and
and 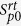 are transformation matrices for the coordinate systems defined in Appendix B of ref. 34, and
are transformation matrices for the coordinate systems defined in Appendix B of ref. 34, and 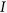 is the identity matrix. From Eqs (19, 20, 21, 22, 23), the absorption rate of the molecule can be expressed as
is the identity matrix. From Eqs (19, 20, 21, 22, 23), the absorption rate of the molecule can be expressed as
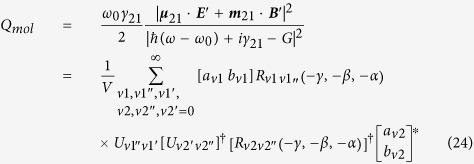 |
with
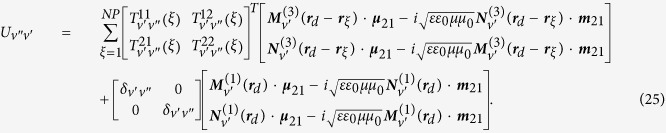 |
Here 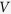 =
=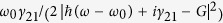 . The method to calculate the resonance broadening function
. The method to calculate the resonance broadening function 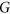 has been described in ref. 25, of which value is independent with the incident wave. From Eqs. (1, 2, 3, 4 in the text, the absorption of NPs can be calculated. The total field around the
has been described in ref. 25, of which value is independent with the incident wave. From Eqs. (1, 2, 3, 4 in the text, the absorption of NPs can be calculated. The total field around the  th NP is given by the following equation
th NP is given by the following equation
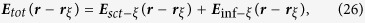 |
where 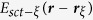 is the total scattered field of the
is the total scattered field of the 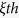 NP, which is expressed as
NP, which is expressed as
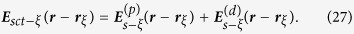 |
Here 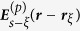 and
and 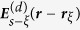 represent the scattered fields of the
represent the scattered fields of the  th particle, which are caused by the external incident field and the irradiative molecule, respectively.
th particle, which are caused by the external incident field and the irradiative molecule, respectively.
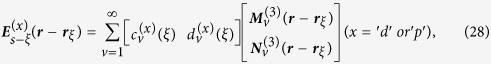 |
where 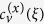 and
and 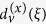 are the expansion coefficients of the scattered wave, which are given by
are the expansion coefficients of the scattered wave, which are given by
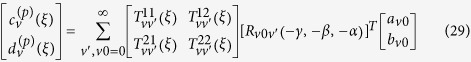 |
and
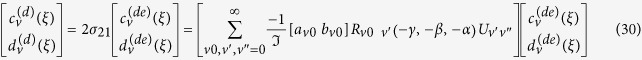 |
with 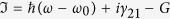 . Here
. Here 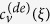 and
and 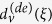 are the expansion coefficients of the scattered wave from the
are the expansion coefficients of the scattered wave from the 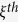 NP irritated by a dipole with a momentum of
NP irritated by a dipole with a momentum of 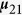 , the calculated method for them can be found in the supplement materials of ref. 25. Similarly,
, the calculated method for them can be found in the supplement materials of ref. 25. Similarly, 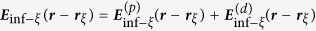 denotes the total incidental wave on the
denotes the total incidental wave on the 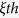 NP, which
NP, which 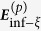 and
and 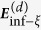 are composed of the excited wave and the scattered fields from other NPs.
are composed of the excited wave and the scattered fields from other NPs.
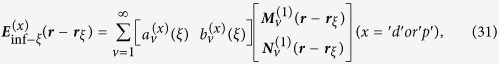 |
where 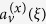 and
and 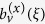 are related to the scattering coefficients
are related to the scattering coefficients 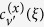 and
and 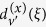 , that is
, that is
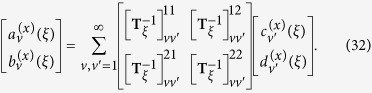 |
Using Eqs. (26, 27), the absorption of NPs can be decomposed into the extinction part and the scattering part:
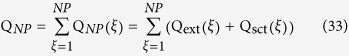 |
with 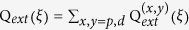 and
and 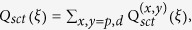 and
and
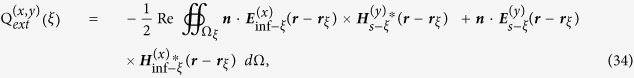 |
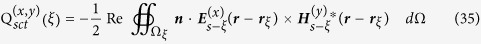 |
Using the orthogonality conditions of the VSFs, we have:
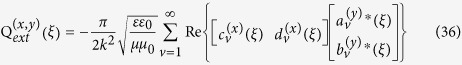 |
and
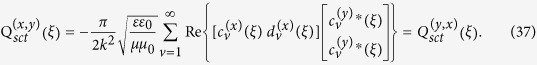 |
From Eqs. (26, 27, 28, 29, we have
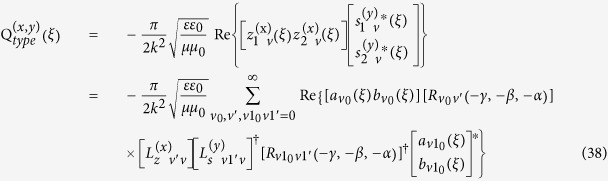 |
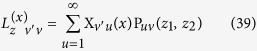 |
with
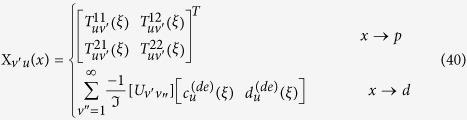 |
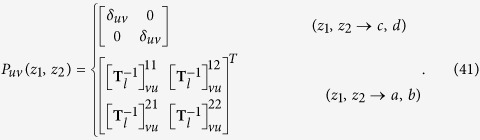 |
Here when ‘type’ is set to be ‘ext’, 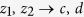 and
and 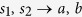 , while
, while 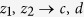 and
and 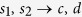 for ‘sct’. From the above equations, Eq. (6) in the text can be obtained.
for ‘sct’. From the above equations, Eq. (6) in the text can be obtained.
Symmetry analysis of
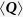
In this section, we present symmetry analysis of 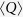 . The expansion coefficients of any wave,
. The expansion coefficients of any wave, 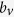 and
and 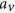 , can also be expressed as59,60
, can also be expressed as59,60
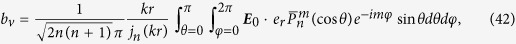 |
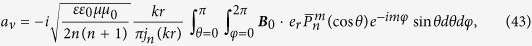 |
where 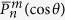 is related to the associated Legendre function, which is given by
is related to the associated Legendre function, which is given by
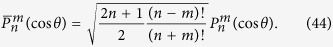 |
If the space inversions are performed for both the NP-molecule system and the incident wave, the absorption rate of the system 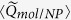 should be unchanged because of parity conservation61. Since the electric field possesses an odd parity while the magnetic field has an even parity, from Eqs. (42) and (43), we have
should be unchanged because of parity conservation61. Since the electric field possesses an odd parity while the magnetic field has an even parity, from Eqs. (42) and (43), we have
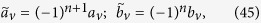 |
where 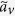 and
and 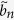 are expansion coefficients of the space inversed incident wave, while
are expansion coefficients of the space inversed incident wave, while 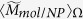 is determined only by the property of the enantiomorphic system. According to Eq. (10) in the main text, we have
is determined only by the property of the enantiomorphic system. According to Eq. (10) in the main text, we have
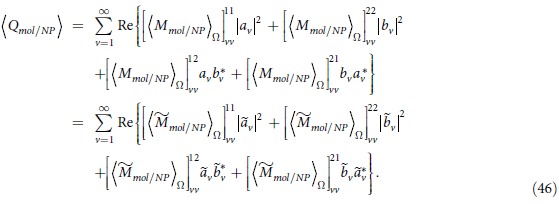 |
Form Eqs (45, 46), it can be seen that 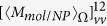 and
and 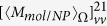 are connected with
are connected with 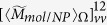 and
and 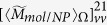 through
through
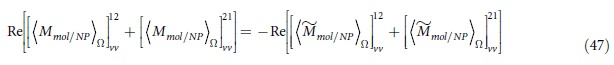 |
and
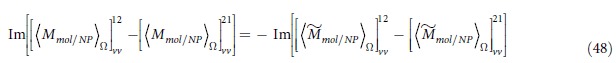 |
At the same time 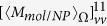 and
and 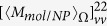 should satisfy
should satisfy
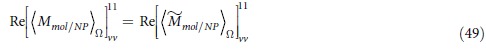 |
and
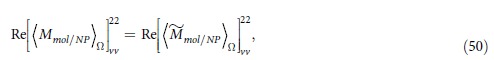 |
if Eq. (46) will be satisfied for all kinds of incident waves.
According to the equations above, the dichroism of the system can be written as
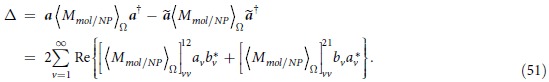 |
For the special case of the OAM beams, Eqs. (10, 11) in the text can be readily gotten.
Additional Information
How to cite this article: Wu, T. et al. Plasmon-induced strong interaction between chiral molecules and orbital angular momentum of light. Sci. Rep. 5, 18003; doi: 10.1038/srep18003 (2015).
Supplementary Material
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 11274042, 61421001 and 11174033).
Footnotes
Author Contributions Numerical results and theoretical method are presented by T.W. the idea and physical analysis are given by X.Z. and R.W. All authors reviewed the manuscript.
References
- Fasman G. D. (ed.) Circular Dichroism and Conformational Analysis of Biomolecules (Plenum Press, 1996). [Google Scholar]
- Wagnière G. H. On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image (Wiley-VCH, 2007). [Google Scholar]
- Berova N., Polavarapu P. L., Nakanishi K. & Woody R. W. Comprehensive Chiroptical Spectroscopy John Wiley and Sons Inc. (2012).
- Patterson D., Schnell M. & Doyle J. M. Enantiomer-specific detection of chiral molecules via microwave spectroscopy. Nature(London, UK) 497, 475−478 (2013). [DOI] [PubMed] [Google Scholar]
- Allen L., Beijersbergen M. W., Spreeuw R. J. C. & Woerdman J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185 (1992). [DOI] [PubMed] [Google Scholar]
- Yao A. M. & Padgett M. J. Orbital angular momentum: origins, behavior and applications. Adv. Opt. Photon. 3, 161–204 (2011). [Google Scholar]
- Mair A., Vaziri A., Weihs G. & Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001). [DOI] [PubMed] [Google Scholar]
- Wang J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics. 6, 488–496 (2012). [Google Scholar]
- Padgett M. & Bowman R. Tweezers with a twist. Nat. Photonics 5, 343–348 (2011). [Google Scholar]
- He H., Friese M. E. J., Heckenberg N. R. & Rubinsztein-Dunlop H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett 75, 826 (1995). [DOI] [PubMed] [Google Scholar]
- Alexandrescu A., Cojoc D. & Di Fabrizio E. Mechanism of angular momentum exchange between molecules and Laguerre-Gaussian beams. Phys. Rev. Lett 96, 243001 (2006). [DOI] [PubMed] [Google Scholar]
- Jáuregui R. Rotational effects of twisted light on atoms beyond the paraxial approximation. Phys. Rev.A 70, 033415 (2004). [Google Scholar]
- Mondal P. K., Deb B. & Majumder S. Angular momentum transfer in interaction of Laguerre-Gaussian beams with atoms and molecules. Phys. Rev. A 89, 063418 (2014). [Google Scholar]
- Romero L. D., Andrews D. L. & Babiker M. A quantum electrodynamics framework for the nonlinear optics of twisted beams. J. Opt. B 4, S66 (2002). [Google Scholar]
- Andrews D. L., Romero L. D. & Babiker M. On optical vortex interactions with chiral matter. Opt. Commun. 237, 133–139 (2004). [Google Scholar]
- Babiker M., Bennett C. R., Andrews D. L. & Romero L. D. Orbital angular momentum exchange in the interaction of twisted light with molecules. Phys. Rev. Lett. 89, 143601 (2002). [DOI] [PubMed] [Google Scholar]
- Araoka F., Verbiest T., Clays K. & Persoons A. Interactions of twisted light with chiral molecules: an experimental investigation. Phys. Rev. A 71, 055401 (2005). [Google Scholar]
- Löffler W., Broer D. J. & Woerdman J. P. Circular dichroism of cholesteric polymers and the orbital angular momentum of light. Phys. Rev. A 83, 065801 (2011). [Google Scholar]
- Govorov A. O., Fan Z., Hernandez P., Slocik J. M. & Naik R. R. Theory of circular dichroism of nanomaterials comprising chiral molecules and nanocrystals: plasmon enhancement, dipole interactions, and dielectric effects. Nano Lett. 10, 1374–1382 (2010). [DOI] [PubMed] [Google Scholar]
- Maoz B. M. et al. Plasmonic chiroptical response of silver nanoparticles interacting with chiral supramolecular assemblies. J. Am. Chem. Soc. 134, 17807–17813 (2012). [DOI] [PubMed] [Google Scholar]
- Maoz B. M. et al. Amplification of chiroptical activity of chiral biomolecules by surface plasmons. Nano lett. 13, 1203–1209 (2013). [DOI] [PubMed] [Google Scholar]
- Lu F. et al. Discrete nanocubes as plasmonic reporters of molecular chirality. Nano lett. 13, 3145–3151 (2013). [DOI] [PubMed] [Google Scholar]
- Zhang H. & Govorov A. O. Giant circular dichroism of a molecule in a region of strong plasmon resonances between two neighboring gold nanocrystals. Phys Rev. B 87, 075410 (2013). [Google Scholar]
- Liu Y. et al. Strong superchiral field in hot spots and its interaction with chiral molecules. Europhys. Lett. 110, 17008 (2015). [Google Scholar]
- Wu T., Ren J., Wang R. & Zhang X. Competition of Chiroptical Effect Caused by Nanostructure and Chiral Molecules. J. Phys. Chem. C 118, 20529–20537 (2014). [Google Scholar]
- Liu Y., Wang R. & Zhang X. Giant circular dichroism enhancement and chiroptical illusion in hybrid molecule-plasmonic nanostructures. Opt. Express 22, 4357–4370 (2014). [DOI] [PubMed] [Google Scholar]
- Wang R. Y. et al. Experimental observation of giant chiroptical amplification of small chiral molecules by gold nanosphere clusters. J. Phys. Chem. C 118, 9690–9695 (2014). [Google Scholar]
- Ghosh S. K. & Pal T. Interparticle coupling effect on the surface plasmon resonance of gold nanoparticles: from theory to applications. Chem. Rev. 107, 4797–4862 (2007). [DOI] [PubMed] [Google Scholar]
- Willets K. A. & Van Duyne R. P. Localized surface plasmon resonance spectroscopy and sensing. Annu. Rev. Phys. Chem. 58, 267–297 (2007). [DOI] [PubMed] [Google Scholar]
- Hendry E. et al. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 5, 783–787 (2010). [DOI] [PubMed] [Google Scholar]
- Nie S. & Emory S. R. Probing single molecules and single nanoparticles by surface-enhanced Raman scattering. Science 275, 1102–1106 (1997). [DOI] [PubMed] [Google Scholar]
- Xu H., Bjerneld E. J., Käll M. & Börjesson L. Spectroscopy of single hemoglobin molecules by surface enhanced Raman scattering. Phys. Rev. Lett. 83, 4357 (1999). [Google Scholar]
- Chuntonov L. & Haran G. Maximal Raman optical activity in hybrid single molecule-plasmonic nanostructures with multiple dipolar resonances. Nano lett 13, 1285–1290 (2013). [DOI] [PubMed] [Google Scholar]
- Doicu A., Wriedt T. & Eremin Y. A. Light Scattering by Systems of Particles (Springer-Verlag, Berlin, Heidelberg, 2006). [Google Scholar]
- Mishchenko M. I., Travis L. D. & Mackowski D. W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transfer 55, 535–575 (1996). [Google Scholar]
- Kiselev A. D. & Plutenko D. O. Mie scattering of Laguerre-Gaussian beams: Photonic nanojets and near-field optical vortices. Phys. Rev. A 89, 043803 (2014). [Google Scholar]
- Johnson P. B. & Christy R. W. Optical Constants of the Noble Metals. Phys. Rev. B: Solid State 6, 4370−4379 (1972). [Google Scholar]
- Tang Y. & Cohen A. E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 104, 163901 (2010). [DOI] [PubMed] [Google Scholar]
- Cameron R. P., Barnett S. M. & Yao A. M. Optical helicity, optical spin, and related quantities in electromagnetic theory. New J. Phys. 14, 053050 (2012). [Google Scholar]
- Candlin D. J. Analysis of the new conservation law in electromagnetic theory. II Nuovo Cimento 37, 1390–1395 (1965). [Google Scholar]
- Rosales-Guzmán C., Volke-Sepulveda K. & Torres J. P. Light with enhanced optical chirality. Opt. Lett. 37, 3486–3488 (2012). [DOI] [PubMed] [Google Scholar]
- Bekshaev A. A simple analytical model of the angular momentum transformation in strongly focused light beams. Cent. Eur. J. Phys. 8, 947–960 (2010). [Google Scholar]
- Zhao Y. et al. Spin-to-orbital angular momentum conversion in a strongly focused optical beam. Phys. Rev. Lett 99, 073901 (2007). [DOI] [PubMed] [Google Scholar]
- Bliokh K. Y. & Nori F. Characterizing optical chirality. Phys Rev. A 83, 021803 (2011). [Google Scholar]
- Coles M. M. & Andrews D. L. Chirality and angular momentum in optical radiation. Phys Rev. A 85, 063810 (2012). [Google Scholar]
- Fan Z., Zhang H. & Govorov A. O. Optical properties of chiral plasmonic tetramers: circular dichroism and multipole effects. J. Phys. Chem. C 117, 14770–14777 (2013). [Google Scholar]
- Fan Z. & Govorov A. O. Plasmonic circular dichroism of chiral metal nanoparticle assemblies. Nano Lett. 10, 2580–2587 (2010). [DOI] [PubMed] [Google Scholar]
- Tian X., Fang Y. & Zhang B. Multipolar Fano resonances and Fano-assisted optical activity in silver nanorice heterodimers. ACS Photonics 1, 1156–1164 (2014). [Google Scholar]
- Ferry V. E., Smith J. M. & Alivisatos A. P. Symmetry Breaking in Tetrahedral Chiral Plasmonic Nanoparticle Assemblies. ACS Photonics 1, 1189–1196 (2014). [Google Scholar]
- Cathcart N. & Kitaev V. Monodisperse hexagonal silver nanoprisms: synthesis via thiolate-protected cluster precursors and chiral, ligand-imprinted self-assembly. ACS nano 5, 7411–7425 (2011). [DOI] [PubMed] [Google Scholar]
- Kuzyk A. et al. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 483, 311–314 (2012). [DOI] [PubMed] [Google Scholar]
- Shen X. et al. Three-dimensional plasmonic chiral tetramers assembled by DNA origami. Nano lett. 13, 2128–2133 (2013). [DOI] [PubMed] [Google Scholar]
- Wu X. et al. Unexpected chirality of nanoparticle dimers and ultrasensitive chiroplasmonic bioanalysis. J. Am. Chem. Soc. 135, 18629–18636 (2013). [DOI] [PubMed] [Google Scholar]
- Plum E. et al. Metamaterials: optical activity without chirality. Phys. Rev. Lett. 102, 113902 (2009). [DOI] [PubMed] [Google Scholar]
- Yokoyama A., Yoshida M., Ishii A. & Kato Y. K. Giant circular dichroism in individual carbon nanotubes induced by extrinsic chirality. Phys. Rev. X 4, 011005 (2014). [Google Scholar]
- Asenjo-Garcia A. & de Abajo F. G. Dichroism in the Interaction between Vortex Electron Beams, Plasmons, and Molecules. Phys. Rev. Lett. 113, 066102 (2014). [DOI] [PubMed] [Google Scholar]
- Ganic D., Gan X. & Gu M. Focusing of doughnut laser beams by a high numerical-aperture objective in free space. Opt. Express 11, 2747–2752 (2003). [DOI] [PubMed] [Google Scholar]
- Hassey R. et al. Probing the chiroptical response of a single molecule. Science 314, 1437–1439 (2006). [DOI] [PubMed] [Google Scholar]
- Neves Alvaro Ranha, A. et al. Exact partial wave expansion of optical beams with respect to an arbitrary origin. Opt. Lett. 31, 2477–2479 (2006). [DOI] [PubMed] [Google Scholar]
- Gouesbet G. & Lock J. A. List of problems for future research in generalized Lorenz–Mie theories and related topics, review and prospectus [Invited]. Appl. Opt. 52, 897–916 (2013). [DOI] [PubMed] [Google Scholar]
- Barron L. D. Molecular Light Scattering and Optical Activity (Cambridge Univ. Press, Cambridge, UK, 1982). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.