Slow [Na]_i Changes and Positive Feedback Between Membrane Potential and [Ca]_i Underlie Intermittent Early Afterdepolarizations and Arrhythmias

Abstract

Background

Most cardiac arrhythmias occur intermittently. As a cellular precursor of lethal cardiac arrhythmias, early afterdepolarizations (EADs) during action potentials (APs) have been extensively investigated, and mechanisms for the occurrence of EADs on a beat-to-beat basis have been proposed. However, no previous study explains slow fluctuations in EADs, which may underlie intermittency of EAD trains and consequent arrhythmias. We hypothesize that the feedback of intracellular calcium and sodium concentrations ([Na]_i and [Ca]_i) that influence membrane voltage (V) can explain EAD intermittency.

Methods and Results

AP recordings in rabbit ventricular myocytes revealed intermittent EADs, with slow fluctuations between runs of APs with EADs present or absent. We then used dynamical systems analysis and detailed mathematical models of rabbit ventricular myocytes that replicate the observed behavior, and investigated the underlying mechanism. We found that a dominance of inward Na-Ca exchanger current (I_NCX) over Ca-dependent inactivation of L-type Ca current (I_CaL) forms a positive feedback between [Ca]_i and V, thus resulting in two stable AP states; with and without EADs (i.e., bistability). Slow changes in [Na]_i determine the transition between these two states, forming a bistable on-off switch of EADs. Tissue simulations showed that this bistable switch of cellular EADs provided both a trigger and a functional substrate for intermittent arrhythmias in homogeneous tissues.

Conclusions

Our study demonstrates that the interaction among V, [Ca]_i and [Na]_i, causes slow on-off switching (or bistability) of AP duration in cardiac myocytes and EAD-mediated arrhythmias, and suggests a novel possible mechanism for intermittency of cardiac arrhythmias.

Introduction

Cardiac arrhythmias, the leading cause of sudden cardiac death, often occur intermittently in patients. Both premature ventricular complexes and ventricular tachycardia are intermittent phenomena, occurring every few minutes to several days.^{1, 2} As a major cause of cardiac arrhythmias, early afterdepolarization (EAD) can be induced by either spontaneous calcium (Ca) releases and subsequent augmentation of the sodium (Na)-Ca exchanger current (I_NCX) or by voltage (V) related instabilities due to reactivation of L-type Ca (I_CaL)³ or sodium (I_Na) currents.^{4, 5} Regardless of its ionic mechanisms, EAD is sensitive to the net transmembrane current at its takeoff V, whereby an inward or outward shift can turn on or off of EADs. Spontaneous fluctuations between action potentials (APs) with and without EADs have been widely observed experimentally^{6, 7} and in simulations.^{6, 8} Modeling and theoretical studies have related this on-off switch of EADs to the stochastic opening of I_CaL or the chaotic outcome of the interaction between the window I_CaL and K currents.^{9, 10} However, prior work has focused primarily on mechanisms of EAD occurrence on a beat-to-beat basis, but not on how cellular EADs may occur intermittently and cause arrhythmias on a longer time scale. Furthermore, lack of consideration of the interplay among V and [Ca]_i and [Na]_i in previous studies limited our understanding of EAD dynamics and their arrhythmia consequences.¹¹

The interaction between V and [Ca]_i has proven important in the induction of complex V dynamics and subsequent arrhythmia.^{12, 13} However, previous studies focused on conditions favoring Ca instability (such as alternans and oscillations), where cells were abnormally overloaded with Ca,^12-15 and [Na]_i overload was considered relevant in that it contributes to [Ca]_i loading. These limit our understanding of EADs in the absence of Ca instability such as Long QT syndromes (LQTS), where EADs may occur mainly due to V instability (e.g., due to reactivation of I_CaL) favored by prolonged AP duration (APD).^{16, 17} In these situations, EADs further prolong APs, which can increases [Ca]_i via prolonged opening of I_CaL and reduced diastolic time for Ca efflux. The [Ca]_i gain further prolongs AP via augmented inward I_NCX, forming a positive APD-[Ca]_i feedback. These changes in [Ca]_i are also expected to affect [Na]_i, which will in turn affect V stability via Na-dependent I_NCX and Na-K pump current (I_NaK). At higher [Na]_i shifts in both I_NCX and I_NaK can affect APD,¹⁸ but [Na]_i changes over a slower time scale than V and [Ca]_i (e.g, minutes) in cardiac myocytes.¹⁹

In this study, we examined how interactions among V, [Ca]_i and [Na]_i affect the intermittent occurrence of EADs and the on-off switch that controls transitions. We performed experiments in rabbit ventricular myocytes exhibiting an intermittent EADs, i.e., repeating cycles of EADs appearing for numerous consecutive beats followed by trains of APs without EADs (a sort of bistable state). We then used dynamical systems analysis in a computational ventricular myocyte model to investigate the underlying mechanism. We found that a positive feedback between [Ca]_i and V, due to a dominance of inward I_NCX over Ca-dependent inactivation of I_CaL (CDI) causes bistability, i.e., the coexistence of two stable states. Slow changes in [Na]_i cause transitions between one stable steady state at which EADs are seen and a second stable state where EADs are suppressed. Simulations in 2-dimensional tissue also showed how this bistable switch of cellular EADs could contribute to cardiac arrhythmias at the tissue level.

Methods

Experiments

All animal procedures were approved by the University of California Davis animal welfare committee and conform to the Guide for the Care and Use of Laboratory Animals published by the US National Institutes of Health. Rabbit ventricular myocytes were isolated as previously described.²⁰ Briefly, hearts were excised from adult male New Zealand rabbits and mounted on a Langendorff perfusion apparatus. Collagenase and protease were used to digest the hearts at 37°C, followed by mechanical dispersion to yield the single cells. Isolated myocytes were stored at room temperature for up to 8 hours before experiments. The myocytes were allowed to adhere to coverslips for 5-10 min before experiments. Current-clamp recording was done in cell-attached-patch mode to minimize myocyte perturbation. Heat-polished glass pipettes were filled and cells bathed with a normal Tyrode's solution solution containing (in mM): 140 NaCl, 4 KCl, 1 MgCl₂, 1.8 CaCl₂, 5 HEPES free acid, 5 HEPES sodium salt, 11 Glucose, pH 7.4 with NaOH at 37±1°C. AP recordings were performed with an Axopatch 200 amplifier (Molecular Devices) at a sampling rate of 25kHz. APs were elicited every 2 or 3 seconds by injecting supra-threshold depolarizing currents (< 2 fold the diastolic threshold of excitation). After APs reached steady state, partial block of the rapidly activating delayed rectifier K current (I_Kr) with E-4031 (100-200 nM) was used to prolong AP repolarization and favor EAD generation. Data were analyzed using custom-made software written in MATLAB (The MathWorks Inc).

Modeling

To understand the mechanism of experimentally observed intermittent EADs, we used a well-established rabbit ventricular myocyte model, which includes membrane ionic currents and [Ca]_i and [Na]_i dynamics (https://somapp.ucdmc.ucdavis.edu/Pharmacology/bers/).²¹ To enable EAD generation, we shifted the steady-state activation gate of L-type Ca current (I_CaL) by -5 mV and increased the maximum I_CaL conductance by 60% (unless otherwise specified) to facilitate I_CaL reactivation. This approach has been previously implemented for EAD simulation in theoretical studies, and in part mimics alterations of I_CaL in response to β-adrenergic receptor activation²² or oxidative stress.²³ We paced the cell model at a cycle length (CL) of 1.8 s to further prolong repolarization and favor EAD occurrence.¹⁶ Maximum pump rate of the Na-K ATPase (V_NaK) was increased by 20%. Simulations are performed in single cells, and 1D (4.5 cm) and 2D homogeneous tissues (4.5 × 4.5 cm). To speed up simulations, we assumed a rapid equilibrium approximation for three fast buffers (SLL, SLH and CSQN). All model equations were implemented in C++ and solved with an adaptive time step (with the smallest integration time step being 1 μs at the AP upstroke). The electrical diffusion coefficient is 0.001 cm²/ms; the space step is 0.015 cm, roughly the size of a myocyte.

Results

Quasi-periodic on-off switch of EADs in experiments and simulations

We induced EADs in rabbit ventricular myocytes by reducing the rapid delayed rectifier K current (I_Kr). Similar to previous studies,^{6, 9} AP changes from beat to beat (Fig. 1A left) and by switching between two major states: short APs without EADs, and long APs with one or two EADs (Fig. 1A, gray vs. pink box). The fast fluctuations between EAD and no EAD states (stars in Fig. 1B) are expected. But the quasi-periodical on-off switch of EADs at a slow time scale is unprecedented, where the AP mostly maintained the same state for a number of beats before flipping to the other state (Fig. 1A).

Figure 1.

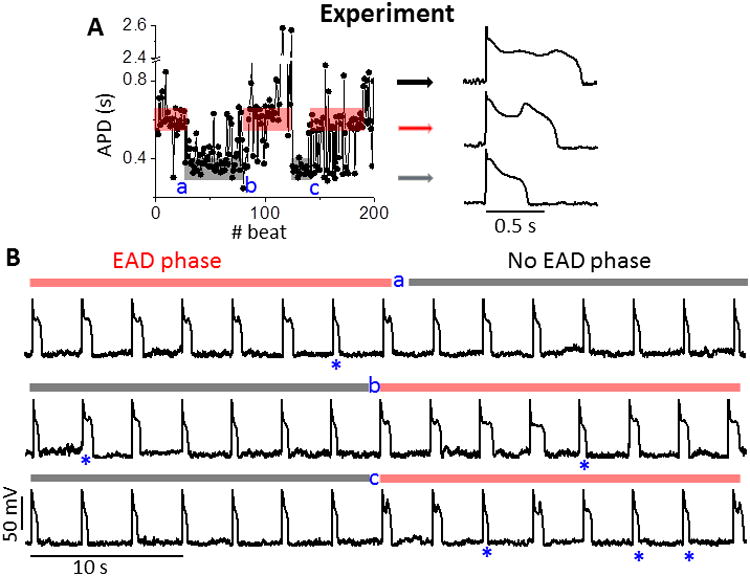
Experimental quasi-periodic on-off switch of EADs. A. APD series (left) measured in a rabbit ventricular myocyte. Quasi-periodic slow transitions of APD between EAD (red shading) and no EAD states (grey shading) are apparent, where a, b and c denote transitions between these two phases. Random jumps in APD also occur amidst these phases. APs with EADs (black/red arrows) and without EADs (gray arrow) are shown. B. AP trains right straddling phase transition points. Only occasional beats (*) interrupt the EAD (red bars) or no EAD phases (gray bars). PCL = 3s.

To understand the mechanisms underlying these previously unreported slow-scale transitions between APs with and without EADs, we performed simulations using a well-established model of the rabbit ventricular AP and Ca transient (CaT). To favor EAD formation in the model, Ca current (I_CaL) conductance (G_Ca) was increased and the activation V-dependence was shifted −5 mV (similar to adrenergic modulation; Fig. 2A, B and D and Fig. S1A). This resulted in EADs induced by I_CaL reactivation (Figs. 1B and S2). Similar to our experiments (Fig. 1B), the abrupt switches between short and long APD states occurred after many beats (Fig. 2D top, shows one full period). APD switches between short and long states (Fig. 2A top), and the long APDs exhibit one or two EADs (defined as a net depolarization during the AP plateau; Fig. 2B top).

Figure 2.

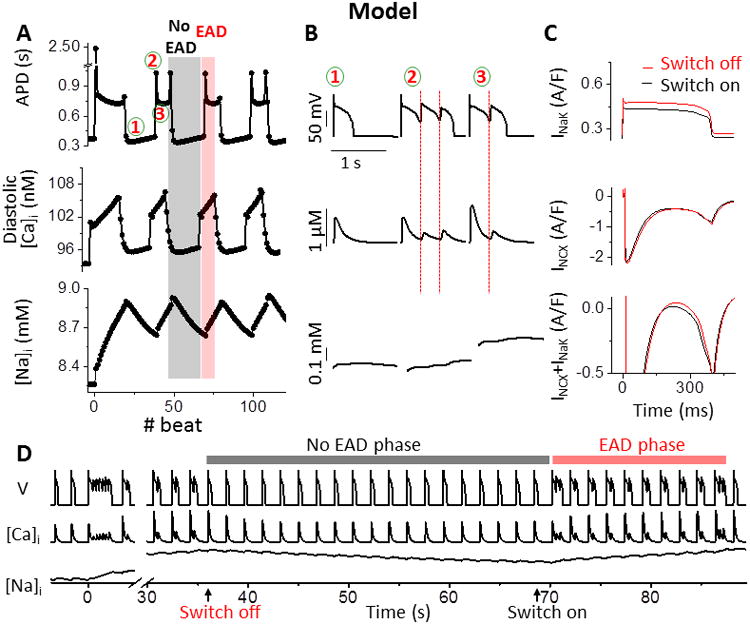
Simulated quasi-periodic on-off switch of EADs. A. Simulated APD, diastolic [Ca]_i, and [Na]_i, showing quasi-periodic switches between short (without EADs, #1) and long APs (with EADs, #2, 3). Gray and red shadings indicate no-EAD and EAD phases. B. Expanded AP, [Ca]_i, and [Na]_i traces at #1, 2 and 3 in A. Red lines indicate time of EAD takeoff, which precedes secondary Ca release (middle). C. Superimposed I_NaK (top), I_NCX (middle) and I_NaK + I_NCX (bottom) at the EAD switch-off (red) and -on (black) beat (i.e., first and last beat of no EAD phase, arrows in panel D). D. AP, [Ca]_i, and [Na]_i from Panel A, showing the transition into intermittent EADs at time 0 (when G_CaL increases) in red and gray shaded regions.

Mechanism of slow-scale EAD on-off switch

Simulations enabled us to investigate mechanisms related to [Ca]_i, [Na]_i and AP dynamics. Diastolic and peak [Ca]_i and sarcoplasmic reticulum (SR) Ca load also exhibit switch-like periods similar to the APD (Fig. 2A, B, and D, and Fig. S3A). In contrast, [Na]_i accumulates (or dissipates) much more gradually (Fig. 2A bottom), reversing direction at the time of APD switch. Small increases in [Na]_i that occur with increasing heart rate are known to shorten APD because of [Na]_i-dependent outward shifts in both Na/Ca exchange and Na/K pump currents (I_NCX and I_NaK) during the delicate balance of AP plateau currents,^{18, 24}.We hypothesize that the slow [Na]_i changes in Fig. 2A might trigger the EAD on and off switches. That is, the progressive rise in [Na]_i during the long APD-EAD phase shifts I_NCX and especially I_NaK outwardly, favoring repolarization, which at a critical point abruptly shortens APD by preventing I_CaL reactivation. Conversely, the gradual dissipation of [Na]_i during the short APD-no EAD phase, shifts I_NCX and I_NaK inwardly, reducing repolarization, which abruptly prolongs APD by favoring I_CaL reactivation (Fig. S2A and B). Indeed, comparing the first and last beat of the no EAD phase (Figs. 2C-D), confirmed that the net [Na]_i-dependent current (I_NCX + I_NaK) is slightly shifted more outward during the switch-off AP plateau (Fig. 2C, red vs. black), which terminates EADs at the switch-off beat by suppressing the reactivation of I_CaL.

Clamping [Na]i abolishes EAD on-off switch and unmasks bistability

How can such a small change in [Na]_i and [Na]_i-dependent net current (Fig. 2A and C) cause abrupt changes in APD (Fig. 2A and D)? To understand this, and considering that [Na]_i changes much more slowly than V and [Ca]_i do, we clamped [Na]_i and reduced the [Ca]_i-[Na]_i-APD system to the [Ca]_i-APD system. Clamping [Na]_i eliminates oscillations in both APD and diastolic [Ca]_i (Fig. 3A-C), but steady state APD and diastolic [Ca]_i still depend on history. If [Na]_i is clamped at 8.8 mM during its decay (the no EAD phase), the APD remains short, and diastolic and peak [Ca]_i stay low (Fig. 3A-C, black). But if the same [Na]_i-clamp (8.8 mM) starts during the EAD phase, APDs remain long and Ca transients large (Fig 3A-C, red). Small perturbations can also cause a jump between these two steady states. For example, a small 1 ms inward current injection during the plateau of a short AP prolongs APD only transiently (Fig. 3D black), but a 1.2% larger current can switch steady-state APs from short to long (with EAD; red). Thus, a sharp threshold current exists, which separates two stable AP states and forms bistability in the reduced system, when [Na]_i is clamped.

Figure 3.

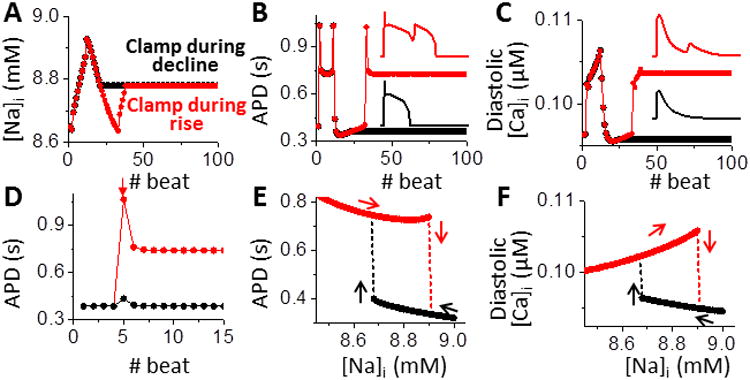
[Na]_i clamping abolishes the EAD on-off switch and unmasks bistability. A. Clamping [Na]_i (at 8.8 mM) during either no EAD (black) or EAD phase (red) eliminates oscillations in both APD (B) and [Ca]_i (C). The phase at the time of [Na]_i-clamp dictates the new stable steady-state APD and [Ca]_i. D. A supra-threshold perturbation (inward current injection, -7.7 A/F for 1 ms, during the AP plateau of 5th beat, arrow) succeeds (red), whereas a 1.2% smaller perturbation fails (black) to switch APD from short to long steady-state. E. Long (with EAD) and short APs (without EAD) coexist over a range of [Na]_i. Switches between long and short APDs (arrows) occur at different [Na]_i, revealing hysteresis. F. Bistability and hysteresis in diastolic [Ca]_i.

Exploring the dependence of both APD and [Ca]_i on [Na]_i (Figs. 3E and F), we found that bistability exists over a range of [Na]_i (∼8.65 to 8.9 mM). Below this range, steady-state long AP with EADs are stable, while above it only short APs occur. Switches between the two quasi-stable states occur at different [Na]_i, (Fig. 3E vertical arrows), and short vs. long APD have opposite effects on slow [Na]_i changes (horizontal arrows), creating a hysteretic loop. Bistability and hysteresis are also seen in diastolic [Ca]_i (Fig. 3F), peak [Ca]_i and SR Ca load (Fig. S3B).

To confirm the existence of bistable APs in the reduced [Ca]_i-APD system ([Na]_i fixed at 8.8 mM), Fig 4A shows an APD map, plotting APD_n as a function of the prior APD (APD_n-1; see Supplemental Material).²⁵ Two discontinuous branches are seen (red), with each intersecting the black identity line (APD_n=APD_n-1) to reveal two stable fixed points (green dots) of the system (slope<1).

Figure 4.

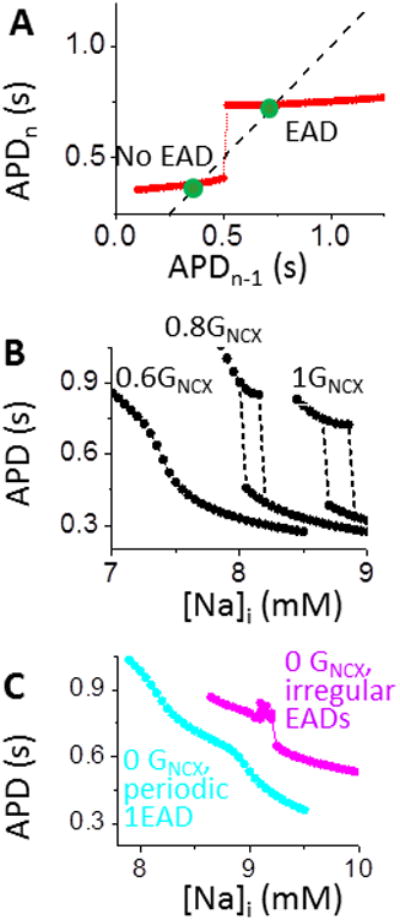
A dominant I_NCX over I_CaL CDI imposes a positive [Ca]_i-APD feedback and underlies bistability. A. APD map shows two discontinuous branches (red). Intersection of identity line (APD_n=APD_n-1) denotes two stable states (green dots). B. Attenuating the positive feedback between APD and [Ca]_i by decreasing G_NCX (not J_NCX) progressively suppresses bistability. C. EAD alone (without positive [Ca]_i-APD feedback by setting G_NCX to 0) fails to produce bistability in either periodic 1 EAD (cyan) or irregular EADs (pink). For details see Supplemental Material, Figs. S5B and C.

A positive [Ca]_i-APD feedback underlies bistability

We next investigated the mechanisms of bistability in the [Ca]_i-APD system (Figs. S4 and 5A). [Ca]_i can affect membrane V bi-directionally. On one hand, high [Ca]_i elevates V by increasing the inward I_NCX and thus prolonging APD; on the other hand, high [Ca]_i reduces V by enhancing Ca-dependent inactivation (CDI) of I_CaL, thus shortening APD. A prolonged APD, in turn, increases [Ca]_i by increasing the Ca influx through I_CaL and limiting diastolic time. Therefore, the [Ca]_i-APD sub-system can have positive or negative feedback between [Ca]_i and APD (Fig. S4B). Although in rabbit heart positive feedback via I_NCX is typically dominant over negative feedback via I_CaL,²⁶ the model allows manipulation either way. We promoted I_CaL dominance on V by decreasing I_NCX.²⁷ To avoid Ca overload-induced instabilities, we only decreased the electrical conductance (G_NCX), but allowed normal Ca extrusion flux (J_NCX; as if NCX were electroneutral). Decreasing G_NCX causes the bistable regime to shrink and disappear (Fig. 4B), suggesting that strong I_NCX is required for bistability. At low G_NCX, EADs can still occur even in the absence of bistability, due to I_CaL reactivation (leftmost curve in Fig. 4B). This implies that a large I_NCX (dominant over I_CaL CDI) is required for establishing a positive [Ca]_i-APD feedback (and hence bistability) but is not required for EAD formation. To further test this, when removing the positive feedback by setting G_NCX=0, we could not induce bistability, even when we additionally reduced K currents to favor EADs (Figs. 4C and S5). We conclude that I_NCX is critical for bistability because of positive [Ca]_i-APD feedback (Figs. 5A and S4B), not simply by causing AP prolongation and EADs.

Figure 5.

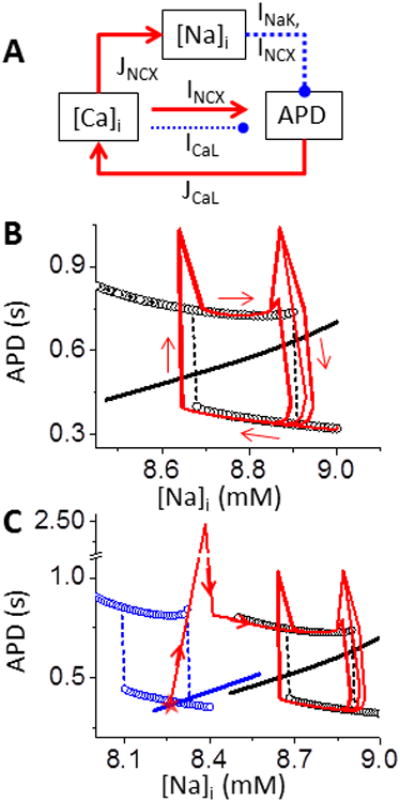
Slow [Na]_i accumulation and depletion constitute an EAD bistable switch. A. Schematic diagram of the interaction between [Na]_i and [Ca]_i-APD. Solid – activation; Dashed - suppression. B. APD-[Na]_i phase plot shows hysteresis loop due to bistability. APD nullcline (circles) and [Na]_i nullcline (black line, calculated by AP clamp in Fig. S1B) do not intersect either stable branch, so APs of the whole system oscillate around the bistable regime (red and arrows). C. Decreasing G_Ca shifts both nullclines to lower [Na]_i (blue), allowing intersection at the low stable branch (red star). Thus, the system stays at a steady-state short AP without EADs (corresponding to traces at t<0 ms in Fig. 2). Red lines and arrows illustrate the APD sequence in Fig.2.

Slow accumulation and dissipation of [Na]_i constitute a slow-scale EAD bistable switch

In the system with [Na]_i unclamped, a rapid increase in [Ca]_i causes [Na]_i accumulation through NCX on a much slower scale. This increased [Na]_i in turn outwardly shifts I_NaK and I_NCX and caused APD shortening (Fig. 5A, top), which limits [Ca]_i loading. Thus, a negative feedback exists between the slow [Na]_i dynamics and the fast [Ca]_i-APD subsystem. In phase plots of APD and [Na]_i, the fast [Ca]_i-APD subsystem shows bistable APD (APD nullclines as black circles in Fig. 5B). The slow [Na]_i variable increases linearly with APD ([Na]_i nullcline, Fig. 5B black line). The intersection of these two nullclines, which identifies the system's fixed point, does not occur in either stable APD nullcline with intermittent EADs, but crosses the unstable branch (Fig. 5B). Thus the APD oscillates around the bistable regime and forms a hysteresis loop (Fig. 5B, red curves), corresponding to the quasi-periodic APD fluctuations at the steady state (Fig. 2). This quasi-periodical oscillation in APD can also be considered a relaxation oscillator, formed by fast positive-feedback-induced bistability and a slow negative feedback in dynamical systems.²⁸

These phase plots also illustrate how intermittent EADs form or are suppressed. For example, when G_CaL is lower the bistable APD regime shifts to lower [Na]_i (Fig. 5C, blue circles). With smaller I_CaL there is also decreased [Ca]_i and [Na]_i, which shifts the [Na]_i nullcline (Fig. 5C, blue line). In this lower I_CaL scenario, the fixed point of the system anchors on the lower stable branch (Fig. 5C, red star), forming a steady short AP without EADs (time <0 s in Fig. 1). But an abrupt increase of G_Ca can prolong APD and generate EADs quickly, shifting to the bistable regime from Fig 5B (red line and arrows in Fig. 5C).

Noise can mask the slow-scale EAD bistable switch

Previous experimental studies of EADs have not identified the intermittency described here. One potential explanation is that noise in the real biological system might mask the bistable switches of EADs (Fig.1A, black). In addition, many cardiac ion channels exhibit refractoriness, which can lead to irregular APD, especially at fast rates.²⁹ Both phenomena may limit the observability of bistable switches and intermittent EADs experimentally.

To examine how biological noise may alter bistability detection, we used Poincaré plots (i.e., APD of the current beat (APD_n) vs. previous beat APD (APD_n-1)). Bistability, as in the model here, leads to two separate clusters (with or without EAD) along the identity line (Fig. 6A(a), red and black circle respectively). On the other hand, if the switch is due to refractoriness, an EAD at APD_n-1 would always lead to a shorter APD_n and vice versa (giving no points in the red circle region). Therefore the clusters in black and red circles along the identity line in these Poincaré plots are consistent with an underlying bistable switch of EADs. Biological noise, due to variance of individual currents during the sensitive plateau phase, will tend to scatter points without specific patterns. This is shown in Fig. 6A, with noise of different amplitudes (σ) applied to membrane V in the model with bistability. Without noise, more than 80% of the total beats are along the identity line (Fig. 6Aa and b left). As the noise level increases, the variability within each cluster increases and more points occur in the top-left and bottom-right quadrants, indicative of individual beats that jump between EAD and no EAD (Fig. 6Aa and b, left to right). Even then, the red EAD cluster is discernable, even under conditions where periodicity is hard to detect in an AP series due to high noise (Fig. 6Ac, blue). We could not detect coexistence of EAD-vs. no EAD clusters in the model without bistability (G_NCX=0), especially with noise (Fig. S6).

Figure 6.

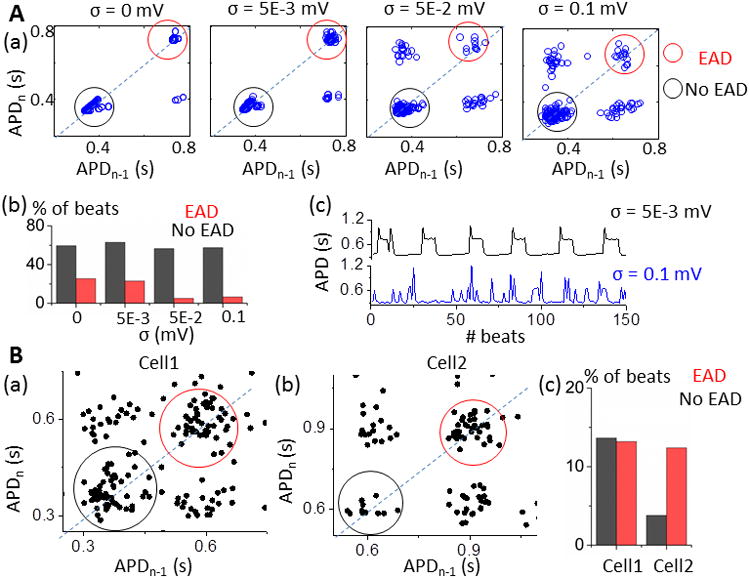
Noise can mask slow-scale bistable EAD switch. A. a) Two separate clusters with (red circle) and without EADs (black circle) coexist in APD Poincaré plots for a model with bistable switch. Noise increases the variability within clusters and effects of refractoriness (points outside EAD-no EAD clusters). b) Fraction of beats in EAD and no EAD cluster (red vs. black) for different noise levels. c) APD series at low vs. high level of noise (amplitude σ=0.005 mV vs. σ=0.1 mV). B. APD Poincaré plots of experimental data show coexistence of EAD-no EAD clusters from cell1 (a, Fig. 1A) and cell2 (b, Fig. S7B and C). c) Fraction of beats in EAD (red) and no EAD clusters (black).

We applied the APD Poincaré analysis to our experimental recordings: Fig. 6B shows results from two cells that clearly demonstrate EAD-and no EAD clusters (Fig. 6Ba is the AP trace in Fig. 1; the Bb AP trace is in Fig. S7B and C). In contrast, two other myocytes did not exhibit the same Poincaré pattern (Fig. S8). We infer that in some cases (half of our small sample) bistability may not be the major mechanism of intermittent EADs. However, since noise obscures even the Poincaré pattern, the negative cases may be equivocal (e.g. Cell 4 vs. 3 in Fig S8).

A bistable AP switch induces intermittent cardiac arrhythmias

How do bistable cellular APs contribute to cardiac arrhythmias at the tissue level? The slow [Na]_i accumulation/dissipation around its bistable regime forms a hysteresis bistable switch (Figs. 1, 2 and 5). One can imagine that cells in different regions of cardiac tissue may be out of phase at either EAD state or no EAD state, depending on their history or initial conditions. Therefore, bistability and hysteresis might (even in homogenous tissue) underlie repolarization heterogeneity, which can cause both conduction block for reentrant arrhythmias and ectopic beats for focal arrhythmias, as demonstrated in our 1D and 2D tissue simulations (Fig. 7).

Figure 7.

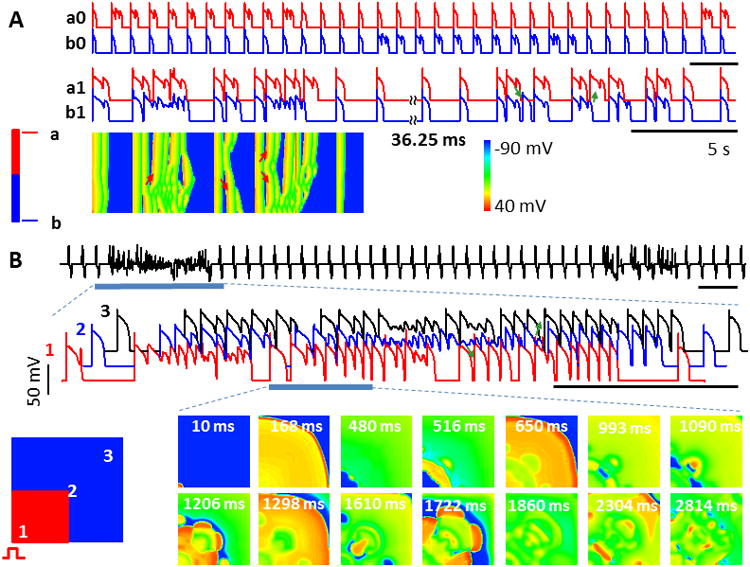
Heterogeneity, ectopic beats and intermittent arrhythmias in homogeneous tissue due to bistable switches. A. Intermittent EAD propagation in 1D cable. APs from top (a0, a1) and bottom (b0, b1) of the cable are shown. Traces a0 and b0 are for uncoupled cells, showing out-of-phase bistable switches due to different initial conditions. When cells are electrically coupled (a1 and b1), EADs propagate intermittently. Space-time plot (bottom) shows one arrhythmic episode. Arrows - EAD propagation. B. APD heterogeneities and ectopic beats form in 2D tissue due to intermittent EAD propagation. Top, pseudo-EKG shows intermittent arrhythmias. Middle, AP trains along the AP propagation during one arrhythmia episode (blue bar below EKG). Bottom, voltage snapshots show complex spatiotemporal patterns. [Na]_i was initially set 0.3 mM higher in the red areas for both 1D cable and 2D tissue.

In a homogenous 1D cable, we set different initial conditions (in [Na]_i) for one half of the cable vs. the other half (Fig. 7A bottom-left, red vs. blue). Before gap-junctional coupling, APs are out of phase in the cable (one end with EADs, the other without; Fig. 7A top, AP traces a0 vs. b0), causing repolarization heterogeneity. When cells are electrically coupled this heterogeneity facilitates EAD propagation (from sites with EADs to those without EADs) and formation of both ectopic beats (Fig. 7A middle, AP traces a1 and b1) and conduction block (manifested by the space-time plot, Fig. 7A bottom). EADs occur intermittently in all cells, but can propagate bi-directionally as they do in homogeneous tissue (arrows, Fig. 7A). Heterogeneous initial conditions in variables other than [Na]_i can also lead to repolarization heterogeneity and PVCs, as long as they set cells at different phases (EAD vs. no EAD, not shown).

In a homogeneous 2D tissue, we set different initial conditions for the left-bottom quarter vs. the remaining portion of tissue (Fig. 7B bottom-left, red vs. blue). Periodic pacing was applied at the left-bottom corner. We recorded the pseudo-electrocardiogram (pEKG) (Fig. 7B top) and three voltage traces along wave propagation (Fig. 7B middle, AP traces 1, 2 and 3). EADs propagate and form ectopic beats as shown in the AP recordings (Fig. 7B middle, arrows). To exemplify the spatiotemporal dynamics, we show voltage snapshots for part of the arrhythmias (blue bar) (Fig. 7B bottom panels). EAD propagates from the EAD area other than the pacing site (snapshots at t=480, 516 ms) and forms ectopic beat (t=650 ms). As the firing rate of focal sites is much faster than the pacing rate, it interacts with the wave back of APs initiating from the pacing site, resulting in conduction block and reentry (snapshots at t=1206, 1610 ms). These interactions generate complex spatiotemporal patterns with highly irregular electrical activity (snapshots at t=2814 ms) before self-terminating.

Interestingly, arrhythmias caused by bistability occur intermittently in both 1D cable (Fig. 7A middle, AP traces) and 2D tissue (Fig. 7B top, pEKG). Since EADs occur quasi-periodically as a result of bistability and hysteresis, the long-and-short APD pattern occur out-of-phase in space intermittently (Fig. 7A top). Therefore, the repolarization heterogeneity and/or EAD propagation spontaneously occur and terminate repetitively, giving rise to intermittent arrhythmias that are often observed in both clinics and experiments. Complex tissue dynamics of course would make observed intermittent arrhythmias like this difficult to connect mechanistically to the fundamental myocyte bistability discussed here. But that is indeed the underlying basis of the arrhythmic pattern in this simulation.

Discussion

In this study we used a computational model and discovered how slow fluctuations in [Na]_i can cause intermittency in cardiac AP dynamics, with APD fluctuating between normal (no EAD) and abnormal (EADs). The main findings are: 1) bistable APs (with and without EADs) can arise when [Na]_i is fixed and require positive [Ca]_i-APD feedback; 2) this bistability leads to intermittent EADs, whereby APs switch quasi-periodically between long APs with EADs and short APs without EADs as [Na]_i slowly accumulates or dissipates around its bistable regime; experimental AP recordings showed intermittent EADs similar to those shown in simulations; 3) biological noise can mask underlying bistability, making it more difficult to discern experimentally; 4) intermittent EADs provide both an arrhythmia trigger and a substrate (causing repolarization heterogeneity) in homogeneous tissue, and induce both reentrant and focal arrhythmias intermittently in cardiac tissue. We propose bistability as a novel mechanism for the switch-on and off of EADs and for EAD-induced arrhythmias, and offer a plausible mechanistic explanation for some of the intermittent of cardiac arrhythmias widely observed both clinically and experimentally.^{1, 2, 30}

Instability arises from the interaction among Ca and Na homeostasis and EADs

The cardiac AP is shaped by the balance between inward and outward currents, which interact with varying [Ca]_i and [Na]_i during the cardiac cycle. Fluxes of both Ca and Na are critical for stable AP and efficient contraction.¹¹ Instabilities in Ca cycling, such as Ca alternans, oscillations and waves, can lead to membrane potential instabilities and cause arrhythmias.^12-15 Na instabilities are mainly seen when [Na]_i is elevated (as in heart failure;¹⁹), which increase Ca loading and thus Ca-mediated membrane potential instability.³¹ However, large (∼mM) changes in global [Na]_i are unlikely to occur in a short time,^{18, 32} and the contribution of [Na]_i to arrhythmias has been overlooked due to its slower dynamics (minutes³³) compared to rapid changes in V and [Ca]_i. Here we found that interaction between a stable Ca cycling and EADs is capable of inducing bistability (Figs. 3 and 4), and the slow [Na]_i dynamics (even within the physiological range) can cause the abrupt APD changes (Figs. 2 and 5) and arrhythmias (Fig. 7). Note that not only does the turn-on and -off of EADs alter [Ca]_i and [Na]_i, but also changes in [Ca]_i or [Na]_i in turn regulate the switching on and off of EADs.

Mechanisms underlying EAD on-off switch

Irregular beat-to-beat transitions between EAD and no EAD beats have been studied in previous experiments^{7, 8} and simulations,^{6, 9} and attributed to refractoriness, biological noise, or both.^{6, 8, 9} Previous studies showed that [Ca]_i accumulation during the EAD period causes elevation of [Na]_i, which then terminates the EADs.³² In our experiments, we observed both of these fast-scale and slow-scale switches (Fig. 1), and our simulations and analysis demonstrate that a bistable switch underlies the latter. Using APD Poincaré plots, we suggest that a bistable switch-on and off of EADs may be common, and exist even in the presence of apparently irregular APD sequences (Fig. 6Bb and Fig. S7B) and be masked by noise, which makes the bistable states less detectable when only inspecting AP or APD traces (such as that in Fig. S7C and B right). We acknowledge that while bistability is consistent with the presence of these two clusters in the APD Poincaré plots, other cardiac memory effects³⁴ may also contribute to the switch-on and off of EADs and allow the coexistence of two clusters with and without EADs. Noise might also account for differences between model and experimental EAD waveforms.

In our model, the EAD on and off switch occurred and was analyzed with stable intracellular Ca cycling. We did not measure [Ca]_i during experiments, but our conditions were likely to prevent spontaneous Ca release during our AP recordings. That is, we expect low SR load in rabbit myocytes paced at slow rates without adrenergic activation. Spontaneous Ca release, which may occur with Ca overload, would complicate interpretation of the mechanisms here and warrants further investigation.

Model-independence of our findings

To what extent do our findings depend on the detailed ionic formulations and parameter values of the computational model used? To answer this question, we consider the conditions required for bistability and hysteresis.

A positive Ca-to-V coupling is required to establish a positive feedback between [Ca]_i and APD (Fig. 4Bb). In this condition, the activation of the inward I_NCX by [Ca]_i is dominant over CDI of I_CaL, so that a larger CaT leads to a longer APD, as seen in a variety of experimental conditions.^{26, 27, 35} Certain pathological conditions where I_NCX and [Na]_i are up-regulated, such as heart failure,³⁶ might favor bistability by strengthening the positive feedback between [Ca]_i and APD (in the presence of EADs) (Figs. 4C-D).

Various types of EADs have been explained by different ionic mechanisms (reviewed by Weiss et al³), including I_CaL reactivation, enhanced Ca release and subsequent NCX augmentation³⁷ and reactivating Na current.^{4, 5} Even when initiated by the same ionic mechanism, EAD waveform and rising rate can vary depending on take-off time and voltage. We argue that independent of the ionic mechanism or waveforms, all that is needed to obtain the nonlinear APD maps (Fig. 4A) necessary for bistability is sensitivity of the EAD to changes in the net transmembrane current at its takeoff, allowing on-and-off behavior.⁶ This tends to occur when EADs are generated by large regenerative inward currents.

As discussed above, the slow dynamics of [Na]_i and its negative regulation of APD¹⁸ allow oscillations around the bistable regime for intermittent EADs (Fig. 5). Alterations of either Ca- or Na-related currents often coexist with EADs in a variety of pathological conditions. These can also alter [Na]_i and push it to its bistable regime and form intermittent EADs.

Altogether, we expect our findings to hold true in any detailed ionic model that satisfies all the above conditions, and to not be parameter-specific. However, the specific [Na]_i, [Ca]_i and APD range in which this bistability occurs would vary with model details, and the above conditions could well be fulfilled by different ionic mechanisms than we have highlighted.

EADs-mediated arrhythmias and bistability

Cardiac arrhythmias are initiated when a triggering event encounters a substrate, i.e., an electrophysiologically vulnerable region of tissue.²⁹ For example, EADs were thought not to propagate in homogenous tissue, unless EADs are chaotic and form dynamical repolarization heterogeneity through chaos de-synchronization.^{9, 38, 39} Here, we found that bistable APs with or without EAD can be induced due to the positive V-[Ca]_i feedback. This bistability amplifies small differences in initial conditions and induces large repolarization heterogeneity by setting cells to different phases without requiring chaotic EADs (Fig. 7). Thus, besides chaos desynchronization, bistability provides another dynamical mechanism for EAD-mediated arrhythmias in homogeneous tissue. The bistable switch between APs with and without EADs provides an arrhythmogenic trigger and can generate large repolarization heterogeneity (substrate) in homogeneous tissue (Fig. 7).

Cardiac arrhythmias are usually transient and intermittent in both experiments and clinics. For example, atrial fibrillation is shown to spontaneously self-terminate and reoccur,³⁰ before becoming chronic (i.e., persistent). Premature ventricular complexes and ventricular tachycardia, which often precede ventricular fibrillation and sudden cardiac death, also occur intermittently.^{1, 2} Cellular EADs found in most studies, especially in simulations,^{4, 9, 40} are persistent or transient in nature rather than intermittent, which causes a gap in our understanding of the cellular basis of intermittency of arrhythmias. Regulation at the tissue or organ level, e.g., by sympathetic stimulation, could be involved. For example, repetitive β-adrenergic surge might underlie intermittent arrhythmias in genetic or acquired long QT2 syndrome (LQTS2), where EADs can be induced transiently by β-adrenergic stimulation.^{17, 40} The initial report here of bistable switches between APs with and without EADs, also provides a detailed mechanistic understanding based on known myocyte properties. Bistability and hysteresis found in the present study provide a novel cell-level mechanism for the intermittency of EAD-induced arrhythmias.