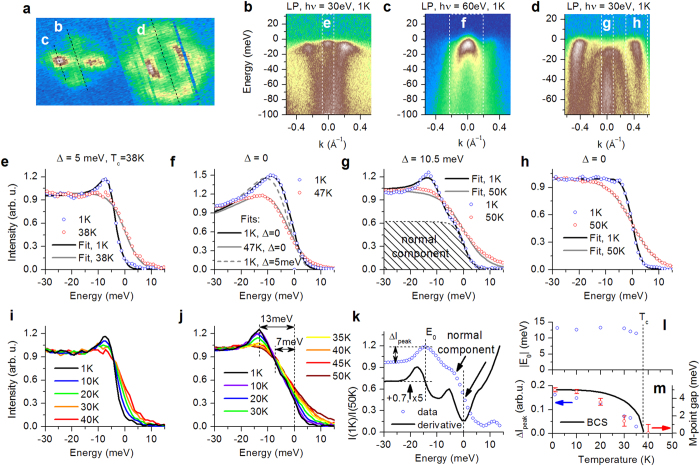
Figure 2.
(a) Crop of Fig. 1a. (b–d) EMCs along the dashed lines in panel (a). All data were recorded at 1 K using a linear polarization and 30 eV (b,d) or 60 eV (c) photon energy. Normal-state (at 50 K) counterpart of the EMC in (d), obtained under the same conditions, is shown in Fig. 1i. (e–h) Normalized EDCs integrated in the momentum windows shown as dashed rectangles in panels (b–d). All fits were obtained using the Dynes–like model for integrated EDCs, as described in the text. (i,j) Temperature dependence of the normalized EDCs in (e,g). The dashed lines in (j) indicate (left to right) the location of the quasiparticle coherence peak E0, leading edge of the superconducting component at 1 K, and EF. (k) Ratio (blue open circles) of the normalized EDCs obtained in the superconducting (1 K) and normal (50 K) state in (g), and its first derivative (black solid line; shifted up by 0.7 and multiplied by 5 for clarity). Vertical dashed lines (left to right) mark the location of E0 and EF. The former is further clearly visible as the zero of the first derivative (intersection of the left vertical and lower horizontal dashed lines). The normal component shown in panel (g) produces an inflection point in the derivative and has its leading edge (minimum of the derivative) located at EF. It could originate in a finite contribution to the photoemission signal from outside the sample surface, given the small size of the single crystals (see Methods). (l,m) Temperature dependence of 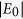 and ΔIpeak defined in panel (k) (blue circles) and of the M-point superconducting gap Δ (extracted from the data in (b,e,i)) (red circles). Black solid line is the temperature dependence expected in the Bardeen-Cooper-Schrieffer theory of superconductivity for Δ = 5 meV and Tc = 38 K. An accurate description of the temperature dependence of these superconducting features would require consistently taking into account the existence of multiple coupled bands and the proximity of their edges to the Fermi level.
and ΔIpeak defined in panel (k) (blue circles) and of the M-point superconducting gap Δ (extracted from the data in (b,e,i)) (red circles). Black solid line is the temperature dependence expected in the Bardeen-Cooper-Schrieffer theory of superconductivity for Δ = 5 meV and Tc = 38 K. An accurate description of the temperature dependence of these superconducting features would require consistently taking into account the existence of multiple coupled bands and the proximity of their edges to the Fermi level.