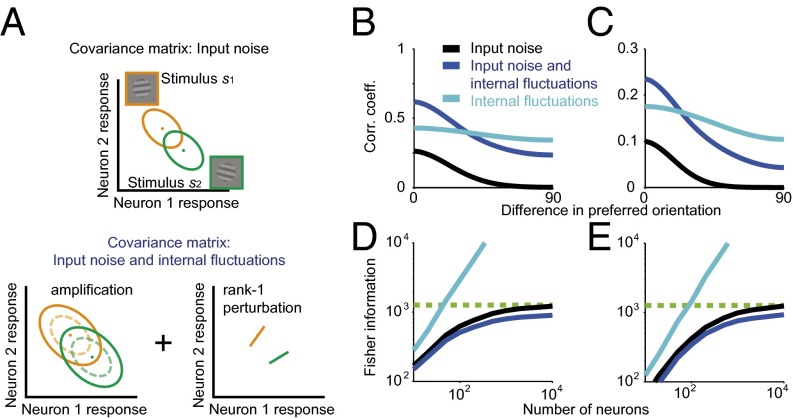
Fig. 5.

Effects of internal global fluctuations on correlations and information. (A) Illustration of the effects of global fluctuations on the noise covariance matrix. (A, Top) Covariance matrices (ellipses) due to input noise around two stimuli (dots represent the mean responses to each stimulus). (A, Bottom) Global fluctuations produce a uniform amplification of the covariances (Left) and an additive, rank-1 perturbation (Right). See SI Appendix, section 6 for derivation. (B) Internal fluctuations increase pairwise noise correlations approximately uniformly (dark blue) compared with the model with peripheral noise alone (black). In the absence of peripheral noise, internal fluctuations produce correlations that depend only weakly on the difference in preferred orientation when averaged over the entire population (light blue). Note that in these simulations the neurons have completely overlapping receptive fields and hence the large correlations. (C) Same as B, but with heterogeneous instead of homogeneous filters. (D) Internal fluctuations can reduce asymptotic information when considered in a model with peripheral noise (compare dark blue and black). In a model without peripheral noise, internal fluctuations do not limit asymptotic information (light blue). (E) Same as D, but with heterogeneous instead of homogeneous filters. Simulation parameters are specified in SI Appendix, Table S3.