SLOPE—ADAPTIVE VARIABLE SELECTION VIA CONVEX OPTIMIZATION

Abstract

We introduce a new estimator for the vector of coefficients β in the linear model y = Xβ + z, where X has dimensions n × p with p possibly larger than n. SLOPE, short for Sorted L-One Penalized Estimation, is the solution to

$$\underset{b\in {ℝ}^p}{min}\frac{1}{2}{\Vert y-Xb\Vert }_{{\ell }_2}^2+{\mathrm{\lambda }}_1{|b|}_{(1)}+{\mathrm{\lambda }}_2{|b|}_{(2)}+\cdots +{\mathrm{\lambda }}_p{|b|}_{(p)},$$

where λ₁ ≥ λ₂ ≥ … ≥ λ_p ≥ 0 and ${|b|}_{(1)}\ge {|b|}_{(2)}\ge \cdots \ge {|b|}_{(p)}$ are the decreasing absolute values of the entries of b. This is a convex program and we demonstrate a solution algorithm whose computational complexity is roughly comparable to that of classical ℓ₁ procedures such as the Lasso. Here, the regularizer is a sorted ℓ₁ norm, which penalizes the regression coefficients according to their rank: the higher the rank—that is, stronger the signal—the larger the penalty. This is similar to the Benjamini and Hochberg [J. Roy. Statist. Soc. Ser. B 57 (1995) 289–300] procedure (BH) which compares more significant p-values with more stringent thresholds. One notable choice of the sequence {λ_i} is given by the BH critical values ${\mathrm{\lambda }}_{\text{BH}}(i)=z(1-i\cdot q/2p)$, where q ∈ (0, 1) and z(α) is the quantile of a standard normal distribution. SLOPE aims to provide finite sample guarantees on the selected model; of special interest is the false discovery rate (FDR), defined as the expected proportion of irrelevant regressors among all selected predictors. Under orthogonal designs, SLOPE with λ_BH provably controls FDR at level q. Moreover, it also appears to have appreciable inferential properties under more general designs X while having substantial power, as demonstrated in a series of experiments running on both simulated and real data.

Introduction

Analyzing and extracting information from data sets where the number of observations n is smaller than the number of variables p is one of the challenges of the present “big-data” world. In response, the statistics literature of the past two decades documents the development of a variety of methodological approaches to address this challenge. A frequently discussed problem is that of linking, through a linear model, a response variable y to a set of predictors {X_j} taken from a very large family of possible explanatory variables. In this context, the Lasso [Tibshirani (1996)] and the Dantzig selector [Candes and Tao (2007)], for example, are computationally attractive procedures offering some theoretical guarantees, and with consequent widespread application. In spite of this, there are some scientific problems where the outcome of these procedures is not entirely satisfying, as they do not come with a machinery allowing us to make inferential statements on the validity of selected models in finite samples. To illustrate this, we resort to an example.

Consider a study where a geneticist has collected information about n individuals by having identified and measured all p possible genetics variants in a genomic region. The geneticist wishes to discover which variants cause a certain biological phenomenon, such as an increase in blood cholesterol level. Measuring cholesterol levels in a new individual is cheaper and faster than scoring his or her genetic variants, so that predicting y in future samples given the value of the relevant covariates is not an important goal. Instead, correctly identifying functional variants is relevant. A genetic polymorphism correctly implicated in the determination of cholesterol levels points to a specific gene and to a biological pathway that might not be previously known to be related to blood lipid levels and, therefore, promotes an increase in our understanding of biological mechanisms, as well as providing targets for drug development. On the other hand, the erroneous discovery of an association between a genetic variant and cholesterol levels will translate to a considerable waste of time and money, which will be spent in trying to verify this association with direct manipulation experiments. It is worth emphasizing that some of the genetic variants in the study have a biological effect while others do not—there is a ground truth that statisticians can aim to discover. To be able to share the results with the scientific community in a convincing manner, the researcher needs to be able to attach some finite sample confidence statements to his/her findings. In a more abstract language, our geneticist would need a tool that privileges correct model selection over minimization of prediction error, and would allow for inferential statements to be made on the validity of his/her selections. This paper presents a new methodology that attempts to address some of these needs.

We imagine that the n-dimensional response vector y is truly generated by a linear model of the form

$y=X\beta +z,$

with X an n × p design matrix, β a p-dimensional vector of regression coefficients and z an n×1 vector of random errors. We assume that all relevant variables (those with β_i ≠ 0) are measured in addition to a large number of irrelevant ones. As any statistician knows, these assumptions are quite restrictive, but they are a widely accepted starting point. To formalize our goal, namely, the selection of important variables accompanied by a finite sample confidence statement, we seek a procedure that controls the expected proportion of irrelevant variables among the selected. In a scientific context where selecting a variable corresponds to making a discovery, we aim at controlling the False Discovery Rate (FDR). The FDR is of course a well-recognized measure of global error in multiple testing and effective procedures to control it are available: indeed, the Benjamini and Hochberg (1995) procedure (BH) inspired the present proposal. The connection between multiple testing and model selection has been made before [see, e.g., Abramovich and Benjamini (1995), Abramovich et al. (2006), Bauer, Pötscher and Hackl (1988), Foster and George (1994) and Bogdan, Ghosh and Żak-Szatkowska (2008)] and others in recent literature have tackled the challenges encountered by our geneticists: we will discuss the differences between our approach and others in later sections as appropriate. The procedure we introduce in this paper is, however, entirely new. Variable selection is achieved by solving a convex problem not previously considered in the statistical literature, and which marries the advantages of ℓ₁ penalization with the adaptivity inherent in strategies like BH.

Section 1 of this paper introduces SLOPE, our novel penalization strategy, motivates its construction in the context of orthogonal designs, and places it in the context of current knowledge of effective model selection strategies. Section 2 describes the algorithm we developed and implemented to find SLOPE estimates. Section 3 showcases the application of our novel procedure in a variety of settings: we illustrate how it effectively solves a multiple testing problem with positively correlated test statistics; we discuss how regularizing parameters should be chosen in nonorthogonal designs; we investigate the robustness of SLOPE to some violations of model assumptions and we apply it to a genetic data set, not unlike our idealized example. Section 4 concludes the paper with a discussion comparing our methodology to other recently introduced proposals as well as outlining open problems.

1. Sorted L-One Penalized Estimation (SLOPE)

1.1. Adaptive penalization and multiple testing in orthogonal designs

To build intuition behind SLOPE, which encompasses our proposal for model selection in situations where p > n, we begin by considering the case of orthogonal designs and i.i.d. Gaussian errors with known standard deviation, as this makes the connection between model selection and multiple testing natural. Since the design is orthogonal, X^′X = I_p, and the regression y = Xβ + z with $z\sim \mathcal{N}(0,{\sigma }^2{I}_n)$ can be recast as

$$\tilde{y}=X^{\prime }y=X^{\prime }X\beta +X^{\prime }z=\beta +X^{\prime }z\sim \mathcal{N}(\beta ,{\sigma }^2{I}_p).$$ (1.1)

In some sense, the problem of selecting the correct model reduces to the problem of testing the p hypotheses H_0,j : β_j = 0 versus two-sided alternatives H_1,j β_i ≠ 0. When p is large, a multiple comparison correction strategy is called for and we consider two popular procedures:

• Bonferroni’s method. To control the familywise error rate⁶ (FWER) at level α ∈ [0, 1], one can apply Bonferroni’s method, and reject H_0,j if $|{\tilde{y}}_j|/\sigma >{\mathrm{\Phi }}^{-1}(1-\alpha /2p)$, where Φ⁻¹(α) is the αth quantile of the standard normal distribution. Hence, Bonferroni’s method defines a comparison threshold that depends only on the number of covariates, p, and the noise level.

• Benjamini–Hochberg step-up procedure. To control the FDR at level q∈ [0, 1], BH begins by sorting the entries of $\tilde{y}$ in decreasing order of magnitude, ${|\tilde{y}|}_{(1)}\ge {|\tilde{y}|}_{(2)}\ge \cdots \ge {|\tilde{y}|}_{(p)}$, which yields corresponding ordered hypotheses H₍₁₎, …, H_(p). [Note that here, as in the rest of the paper, (1) indicates the largest element of a set, instead of the smallest. This breaking with common convention allows us to keep (1) as the index for the most “interesting” hypothesis]. Then BH rejects all hypotheses H_(i) for which i ≤ i_BH, where i_BH is defined by

$$\begin{array}{ll}{i}_{\text{BH}}=max\{i:{|\tilde{y}|}_{(i)}/\sigma \ge {\mathrm{\Phi }}^{-1}(1-q_i)\},\hfill & q_i=i\cdot q/2p\hfill \end{array}$$ (1.2)

(with the convention that i_BH = 0 if the set above is empty). Letting V (resp., R) be the total number of false rejections (resp., total number of rejections), Benjamini and Hochberg (1995) showed that for BH

$$\text{FDR}=\mathbb{E}\left[\frac{V}{R\vee 1}\right]=q\frac{p_0}{p},$$ (1.3)

where p₀ is the number of true null hypotheses, $p0:=|\{i:{\beta }_i=0\}|=p-{\Vert \beta \Vert }_{{\ell }_0}$.

In contrast to Bonferroni’s method, BH is an adaptive procedure in the sense that the threshold for rejection ${|y|}_{(i_{\text{BH}})}$ is defined in a data-dependent fashion, and is sensitive to the sparsity and magnitude of the true signals. In a setting where there are many large β_j ’s, the last selected variable needs to pass a far less stringent threshold than it would in a situation where no β_j is truly different from 0. It has been shown in a variety of papers [see, e.g., Abramovich et al. (2006), Bogdan et al. (2011), Frommlet and Bogdan (2013), Wu and Zhou (2013)] that this behavior allows BH to adapt to the unknown signal sparsity, resulting in some important asymptotic optimality properties.

We now consider how the Lasso would behave in this setting. The solution to

$$\underset{b\in {ℝ}^p}{min}\frac{1}{2}{\Vert y-Xb\Vert }_{{\ell }_2}^2+\mathrm{\lambda }{\Vert b\Vert }_{{\ell }_1}$$ (1.4)

in the case of orthogonal designs is given by soft thresholding. In particular, the Lasso estimate ${\widehat{\beta }}_j$ is not zero if and only if $|{\tilde{y}}_j|>\mathrm{\lambda }$. That is, variables are selected using a nonadaptive threshold λ. Mindful of the costs associated with the selection of irrelevant variables, we can control the FWER by setting ${\mathrm{\lambda }}_{\text{Bonf}}=\sigma \cdot {\mathrm{\Phi }}^{-1}\left(1-\alpha /2p\right)\approx \sigma \cdot \sqrt{2\text{log}p}$.⁷ This choice, however, is likely to result in a loss of power, and may not strike the right balance between errors of type I and missed discoveries. Choosing a value of λ substantially smaller than λ_Bonf in a nondata dependent fashion would lead to a loss not only of FWER control, but also of FDR control since FDR and FWER are identical measures under the global null in which all our variables are irrelevant. Another strategy is to use cross-validation. However, this data-dependent approach for selecting the regularization parameter λ targets the minimization of prediction error, and does not offer guarantees with respect to model selection (see Section 1.3.3). Our idea to achieve adaptivity, thereby increasing power while controlling some form of type-one error, is to break the monolithic penalty $\mathrm{\lambda }{\Vert \beta \Vert }_{{\ell }_1}$, which treats every variable in the same manner. Set

$$\begin{array}{ll}{\mathrm{\lambda }}_{\text{BH}}(i)\stackrel{\text{def}}{=}{\mathrm{\Phi }}^{-1}(1-q_i),\hfill & q_i=i\cdot q/2p,\hfill \end{array}$$

and consider the following program:

$$\underset{b\in {ℝ}^p}{min}\frac{1}{2}{\Vert y-Xb\Vert }_{{\ell }_2}^2+\sigma \cdot {\displaystyle \sum _{i=1}^p{\mathrm{\lambda }}_{\text{BH}}(i)}{|b|}_{(i)},$$ (1.5)

where |b|₍₁₎ ≥ |b|₍₂₎ ≥ ⋯ ≥ |b|_(p) are the order statistics of the absolute values of the coordinates of b: in (1.5) different variables receive different levels of penalization depending on their relative importance. While the similarities of (1.5) with BH are evident, the solution to (1.5) is not a series of scalar-thresholding operations: the procedures are not—even in this case of orthogonal variables–exactly equivalent. Nevertheless, an upper bound on FDR proved in the supplementary appendix [Bogdan et al. (2015)] can still be assured.

THEOREM 1.1

In the linear model with orthogonal design X and $z\sim \mathcal{N}(0,{\sigma }^2{I}_n)$, the procedure (1.5) rejecting hypotheses for which ${\widehat{\beta }}_j\ne 0$ has an FDR obeying

$$\text{FDR}=\mathbb{E}\left[\frac{V}{R\vee 1}\right]\le q\frac{p_0}{p}.$$ (1.6)

Figure 1 illustrates the FDR achieved by (1.5) in simulations using a 5000 × 5000 orthogonal design X and nonzero regression coefficients equal to $5\sqrt{2\text{log}p}$.

FIG. 1.

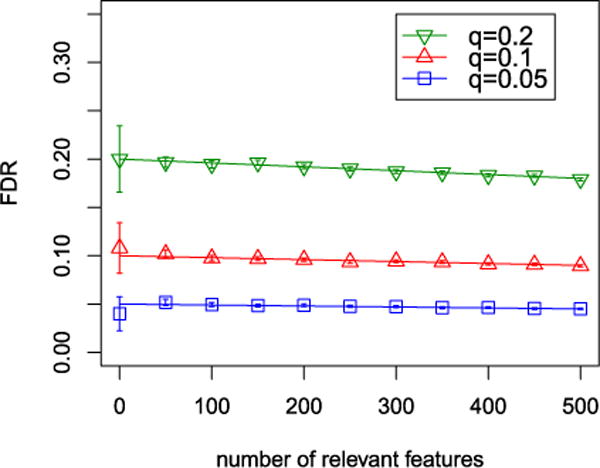
FDR of (1.5) in an orthogonal setting in which n = p = 5000. Straight lines correspond to q · p₀/p, marked points indicate the average False Discovery Proportion (FDP) across 500 replicates, and bars correspond to ±2 SE.

We conclude this section with several remarks describing the properties of our procedure under orthogonal designs:

1. While the λ_BH(i)’s are chosen with reference to BH, (1.5) is neither equivalent to the step-up procedure described above nor to the step-down version.⁸

2. The proposal (1.5) is sandwiched between the step-down and step-up procedures in the sense that it rejects at most as many hypotheses as the step-up procedure and at least as many as the step-down cousin, also known to control the FDR [Sarkar (2002)].

3. The fact that (1.5) controls FDR is not a trivial consequence of this sandwiching.

The observations above reinforce the fact that (1.5) is different from the procedure known as FDR thresholding developed by Abramovich and Benjamini (1995) in the context of wavelet estimation and later analyzed in Abramovich et al. (2006). With $t_{\text{FDR}}={|\tilde{y}|}_{\left(i_{\text{BH}}\right)}$, FDR thresholding sets

$${\widehat{\beta }}_i=\{\begin{array}{ll}{\tilde{y}}_i,\hfill & |{\tilde{y}}_i|\ge t_{\text{FDR}},\hfill \\ 0,\hfill & |{\tilde{y}}_i|<t_{\text{FDR}}.\hfill \end{array}$$ (1.7)

This is a hard-thresholding estimate but with a data-dependent threshold: the threshold decreases as more components are judged to be statistically significant. It has been shown that this simple estimate is asymptotically minimax throughout a range of sparsity classes [Abramovich et al. (2006)]. Our method is similar in the sense that it also chooses an adaptive threshold reflecting the BH procedure. However, it does not produce a hard-thresholding estimate. Rather, owing to nature of the sorted ℓ₁ norm, it outputs a sort of soft-thresholding estimate. A substantial difference is that FDR thresholding (1.7) is designed specifically for orthogonal designs, whereas the formulation (1.5) can be employed for arbitrary design matrices leading to efficient algorithms. Aside from algorithmic issues, the choice of the λ sequence is, however, generally challenging.

1.2. SLOPE

While orthogonal designs have helped us define the program (1.5), this penalized estimation strategy is clearly applicable in more general settings. To make this explicit, it is useful to introduce the sorted ℓ₁ norm: letting λ ≠ 0 be a nonincreasing sequence of nonnegative scalars,

$${\mathrm{\lambda }}_1\ge {\mathrm{\lambda }}_2\ge \cdots \ge {\mathrm{\lambda }}_p\ge 0,$$ (1.8)

we define the sorted-ℓ₁ norm of a vector b ∈ ℝ^p as⁹

$$J_{\mathrm{\lambda }}(b){=\mathrm{\lambda }}_1{|b|}_{(1)}+{\mathrm{\lambda }}_2{|b|}_{(2)}+\cdots +{\mathrm{\lambda }}_p{|b|}_{(p)}.$$ (1.9)

PROPOSITION 1.2

The functional (1.9) is a norm provided (1.8) holds.

The proof of Proposition 1.2 is provided in the supplementary appendix [Bogdan et al. (2015)]. Now define SLOPE as the solution to

$$\begin{array}{ll}\text{minimize}\hfill & \frac{1}{2}{\Vert y-Xb\Vert }^2+{\displaystyle \sum _{i=1}^p{\mathrm{\lambda }}_i{|b|}_{(i)}.}\hfill \end{array}$$ (1.10)

As a convex program, SLOPE is tractable: as a matter of fact, we shall see in Section 2 that its computational cost is roughly the same as that of the Lasso. Just as the sorted ℓ₁ norm is an extension of the ℓ₁ norm, SLOPE can be also viewed as an extension of the Lasso. SLOPE’s general formulation, however, allows to achieve the adaptivity we discussed earlier. The case of orthogonal regressors suggests one particular choice of a λ sequence and we will discuss others in later sections.

1.3. Relationship to other model selection strategies

Our purpose is to bring the program (1.10) to the attention of the statistical community: this is a computational tractable proposal for which we provide robust algorithms; it is very similar to BH when the design is orthogonal, and has promising properties in terms of FDR control for general designs. We now compare it with two other commonly used approaches to model selection: methods based on the minimization of ℓ₀ penalties and the adaptive Lasso. We discuss these here because they allow us to emphasize the motivation and characteristics of the SLOPE algorithm. We also note that the last few years have witnessed a substantive push toward the development of an inferential framework after selection [see, e.g., Benjamini and Yekutieli (2005), Berk et al. (2013), Bühlmann (2013), Efron (2011), Javanmard and Montanari (2014a, 2014b), Lockhart et al. (2014), Meinshausen and Bühlmann (2010), Meinshausen, Meier and Bühlmann (2009), van de Geer et al. (2014), Wasserman and Roeder (2009), Zhang and Zhang (2014)], with the exploration of quite different viewpoints. We will comment on the relationships between SLOPE and some of these methods, developed while editing this work, in the discussion section.

1.3.1. Methods based on ℓ₀ penalties

Canonical model selection procedures find estimates $\widehat{\beta }$ by solving

$$\underset{b\in {ℝ}^p}{min}{\Vert y-Xb\Vert }_{{\ell }_2}^2+\mathrm{\lambda }{\Vert b\Vert }_{{\ell }_0},$$ (1.11)

where ${\Vert b\Vert }_{{\ell }_0}$ is the number of nonzero components in b. The idea behind such procedures is to achieve the best possible trade-off between the goodness of fit and the number of variables included in the model. Popular selection procedures such as AIC [Akaike (1974)] and C_p [Mallows (1973)] are of this form: when the errors are i.i.d. $\mathcal{N}(0,{\sigma }^2)$, AIC and C_p take λ = 2σ². In the high-dimensional regime, such a choice typically leads to including very many irrelevant variables, yielding rather poor predictive properties when the true vector of regression coefficients is sparse. In part to remedy this problem, Foster and George (1994) developed the risk inflation criterion (RIC): they proposed using a larger value of λ, effectively proportional to 2σ² log p, where p is the total number of variables in the study. Under orthogonal designs, if we associate nonzero fitted coefficients with rejections, this yields FWER control. Unfortunately, RIC is also rather conservative and, therefore, it may not have much power in detecting variables with nonvanishing regression coefficients unless they are very large.

The above dichotomy has been recognized for some time now and several researchers have proposed more adaptive strategies. One frequently discussed idea in the literature is to let the parameter λ in (1.11) decrease as the number of included variables increases. For instance, when minimizing

$${\Vert y-Xb\Vert }_{{\ell }_2}^2+p({\Vert b\Vert }_{{\ell }_0}),$$

penalties with appealing information- and decision-theoretic properties are roughly of the form

$$\begin{array}{lll}p(k)=2{\sigma }^{2}k\text{log}(p/j)\hfill & \text{or}\hfill & p(k)=2{\sigma }^2{\displaystyle \sum _{1\le j\le k}\text{log}(p/j)}.\hfill \end{array}$$ (1.12)

Among others, we refer the interested reader to Birgé and Massart (2001), Foster and Stine (1999) and to Tibshirani and Knight (1999) for related approaches.

Interestingly, for large p and small k these penalties are close to the FDR related penalty

$$p(k)={\sigma }^2{\displaystyle \sum _{1\le j\le k}{\mathrm{\lambda }}_{\text{BH}}^2(i),}$$ (1.13)

proposed in Abramovich et al. (2006) in the context of the estimation of the vector of normal means, or regression under the orthogonal design (see the preceding section) and further explored in Benjamini and Gavrilov (2009). Due to an implicit control of the number of false discoveries, similar model selection criteria are appealing in gene mapping studies [see, e.g., Frommlet et al. (2012)].

The problem with these selection strategies is that, in general, they are computationally intractable. Solving (1.12) would involve a brute-force search essentially requiring to fit least-squares estimates for all possible subsets of variables. This is not practical for even moderate values of p, for example, for p > 60.

The decaying sequence of the smoothing parameters in SLOPE goes along the line of the adaptive ℓ₀ penalties specified in (1.12), in which the “cost per variable included” decreases as more get selected. However, SLOPE is computationally tractable and can be easily evaluated even for large-dimensional problems.

1.3.2. Adaptive Lasso

Perhaps the most popular alternative to the computationally intractable ℓ₀ penalization methods is the Lasso. We have already discussed some of the limitations of this approach with respect to FDR control and now wish to explore further the connections between SLOPE and variants of this procedure. It is well known that the Lasso estimates of the regression coefficients are biased due to the shrinkage imposed by the ℓ₁ penalty. To increase the accuracy of the estimation of large signals and eliminate some false discoveries, the adaptive or reweighted versions of Lasso were introduced [see, e.g., Zou (2006) or Candès, Wakin and Boyd (2008)]. In these procedures the smoothing parameters λ₁, …, λ_p are adjusted to the unknown signal magnitudes based on some estimates of regression coefficients, perhaps obtained through previous iterations of Lasso. The idea is then to consider a weighted penalty ${\sum }_i{w}_i|b_i|$, where w_i is inversely proportional to the estimated magnitudes so that large regression coefficients are shrunk less than smaller ones. In some circumstances, such adaptive versions of Lasso outperform its regular version [Zou (2006)].

The idea behind SLOPE is entirely different. In the adaptive Lasso, the penalty tends to decrease as the magnitude of coefficients increases. In our approach, the exact opposite happens. This comes from the fact that we seek to adapt to the unknown signal sparsity and control FDR. As shown in Abramovich et al. (2006), FDR controlling properties can have interesting consequences for estimation. In practice, since the SLOPE sequence λ₁ ≥ ⋯ ≥ λ_p leading to FDR control is typically rather large, we do not recommend using SLOPE directly for the estimation of regression coefficients. Instead we propose the following two-stage procedure: in the first step, SLOPE is used to identify significant predictors; in the second step, the corresponding regression coefficients are estimated using the least-squares method within the identified sparse regression model. Such a two-step procedure, previously proposed in the context of Lasso [see, e.g., Meinshausen (2007)], can be thought of as an extreme case of reweighting, where the selected variables are not penalized while those that are not selected receive an infinite penalty. As shown below, these estimates have very good properties when the coefficient sequence β is sparse.

1.3.3. A first illustrative simulation

To concretely illustrate the specific behavior of SLOPE compared to more traditional penalized approaches, we rely on the simulation of a relatively simple data structure. We set n = p = 5000 and generate the entries of the design matrix with i.i.d. $\mathcal{N}\left(0,1/n\right)$ entries. The number of true signals k varies between 0 and 50 and their magnitudes are set to ${\beta }_i=\sqrt{2\text{log}p}\approx 4.1$, while the variance of the error term is assumed known and equal to 1. Since the expected value of the maximum of p independent standard normal variables is approximately equal to $\sqrt{2\text{log}p}$ and the whole distribution of the maximum concentrates around this value, this choice of model parameters makes the sparse signal barely distinguishable from the noise because the nonzero means are at the level of the largest null statistics. We refer to, for example, Ingster (1998) for a precise discussion of the limits of detectability in sparse mixtures.

We fit these observations with three procedures: (1) Lasso with parameter ${\mathrm{\lambda }}_{\text{Bonf}}=\sigma \cdot {\mathrm{\Phi }}^{-1}(1-\alpha /2p)$, which controls FWER weakly; (2) Lasso with the smoothing parameter λ_CV chosen with 10-fold cross-validation; (3) SLOPE with a sequence λ₁, …, λ_p defined in Section 3.2.2, expression (3.8). The level α for λ_Bonf and q for FDR control in SLOPE are both set to 0.1. To compensate for the fact that Lasso with λ_Bonf and SLOPE tend to apply a much more stringent penalization than Lasso with λ_CV—which aims to minimize prediction error—we have “de-biased” their resulting $\widehat{\beta }$, using ordinary least squares to estimate the coefficients of the variables selected by Lasso–λ_Bonf and SLOPE [see Meinshausen (2007)].

We compare the procedures on the basis of three criteria: (a) FDR, (b) power, and (c) relative squared error ${\Vert X\widehat{\beta }-X\beta \Vert }_{{\ell }_2}^2/{\Vert X\beta \Vert }_{{\ell }_2}^2$. Note that only the first of these measures is meaningful for the case where k = 0, and in such a case FDR = FWER.

Figure 2 reports the results of 500 independent replicates. The three approaches exhibit quite dramatically different properties with respect to model selection. SLOPE controls FDR at the desired level 0.1 for the explored range of k; as k increases, its power goes from 45% to 70%. Lasso–λ_Bonf has FDR =0.1 at k = 0, and a much lower one for the remaining values of k. This results in a loss of power with respect to SLOPE: irrespective of k, the power is less than 45%. Cross-validation chooses a λ that minimizes an estimate of prediction error, and in our experiments, λ_CV is quite smaller than a penalization parameter chosen with FDR control in mind. This results in greater power than SLOPE, but with a much larger FDR (80% on average).

FIG. 2.

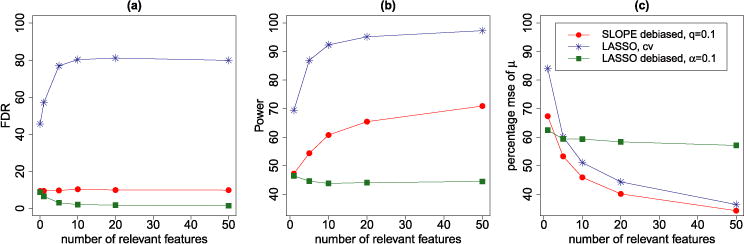
Properties of different procedures as a function of the true number of nonzero regression coefficients: (a) FDR, (b) power, and (c) relative MSE defined as the average of $100\cdot {\Vert \widehat{\mu }-\mu \Vert }_{{\ell }_2}^2/{\Vert \mu \Vert }_{{\ell }_2}^2$ with μ = Xβ, $\widehat{\mu }=X\widehat{\beta }$. The design matrix entries are i.i.d. $\mathcal{N}\left(0,1/n\right),n=p=5000$, all nonzero regression coefficients are equal to $\sqrt{2\text{log}p}\approx 4.13,\text{and}{\sigma }^2=1$. Each point in the figures corresponds to the average of 500 replicates.

Figure 2(c) illustrates the relative mean-square error, which serves as a measure of prediction accuracy. It is remarkable how, despite the fact that Lasso–λ_CV has higher power, SLOPE builds a better predictive model since it has a lower prediction error percentage for all the sparsity levels considered.

2. Algorithms

In this section we present effective algorithms for computing the solution to SLOPE (1.10) which rely on the numerical evaluation of the proximity operator (prox) to the sorted ℓ₁ norm.

2.1. Proximal gradient algorithms

SLOPE is a convex optimization problem of the form

$$\begin{array}{ll}\text{minimize}\hfill & f(b)=g(b)+h(b),\hfill \end{array}$$ (2.1)

where g is smooth and convex, and h is convex but not smooth. In SLOPE, g is the residual sum of squares and, therefore, quadratic, while h is the sorted ℓ₁ norm. A general class of algorithms for solving problems of this kind are known as proximal gradient methods; see Nesterov (2007), Parikh and Boyd (2013) and references therein. These are iterative algorithms operating as follows: at each iteration, we hold a guess b of the solution and compute a local approximation to the smooth term g of the form

$$g(b)+\langle \nabla g(b),x-b\rangle +\frac{1}{2t}{\Vert x-b\Vert }_{{\ell }_2}^2.$$

This is interpreted as the sum of a Taylor approximation of g and of a proximity term; as we shall see, this term is responsible for searching an update reasonably close to the current guess b, and t can be thought of as a step size. Then the next guess b₊ is the unique solution to

$$\begin{array}{l}{b}_{+}=\underset{x}{\text{arg}min}\left\{g(b)+\langle \nabla g(b),x-b\rangle +\frac{1}{2t}{\Vert x-b\Vert }_{{\ell }_2}^2+h(x)\right\}\\ =\underset{x}{\text{arg}min}\left\{\frac{1}{2t}{\Vert (b-t\nabla g(b))-x\Vert }_{{\ell }_2}^2+h(x)\right\}\end{array}$$

(unicity follows from strong convexity). In the literature, the mapping

$$x(y)=\underset{x}{\text{arg}min}\left\{\frac{1}{2t}{\Vert y-x\Vert }_{{\ell }_2}^2+h(x)\right\}$$

is called the proximal mapping or prox for short, and denoted by x = prox_th(y).

The prox of the ℓ₁ norm is given by entry-wise soft thresholding [Parikh and Boyd (2013), page 150] so that a proximal gradient method to solve the Lasso would take the following form: starting with b⁰ ∈ ℝ^p, inductively define

$$b^{k+1}={\eta }_{\mathrm{\lambda }{t}_k}(b^k-t_k{X}^{\prime }(X{b}^k-y);t_k\mathrm{\lambda }),$$

where ${\eta }_{\mathrm{\lambda }}\left(y\right)=\text{sign}\left(y\right)\cdot {\left(|y|-\mathrm{\lambda }\right)}_{+}$ and {t_k} is a sequence of step sizes. Hence, we can solve the Lasso by iterative soft thresholding.

It turns out that one can compute the prox to the sorted ℓ₁ norm in nearly the same amount of time as it takes to apply soft thesholding. In particular, assuming that the entries are sorted (an order p log p operation), we shall demonstrate a linear-time algorithm. Hence, we may consider a proximal gradient method for SLOPE as in Algorithm 1.

It is well known that the algorithm converges [in the sense that f(b^k), where f is the objective functional, converges to the optimal value] under some conditions on the sequence of step sizes {t_k}. Valid choices include step sizes obeying $t_k<2/{\Vert X\Vert }^2$ and step sizes obtained by backtracking line search; see Beck and Teboulle (2009), Becker, Candès and Grant (2011). Further, one can use duality theory to derive concrete stopping criteria; see the supplementary Appendix C [Bogdan et al. (2015)] for details.

Many variants are of course possible and one may entertain accelerated proximal gradient methods in the spirit of FISTA; see Beck and Teboulle (2009) and Nesterov (2004, 2007). The scheme below is adapted from Beck and Teboulle (2009).

Algorithm 1 Proximal gradient algorithm for SLOPE (1.10)
Require: b0 ε ℝp
1:	for k = 0, 1, … do
2:	$b^{k+1}=\text{pro}{x}_{t_k{J}_{\mathrm{\lambda }}}(b^k-t_k{X}^{\prime }(X{b}^k-y))$
3:	end for

Algorithm 2 Accelerated proximal gradient algorithm for SLOPE (1.10)
Require: b0 ε ℝp, and set a0 = b0 and θ0 = 1
1:	for k = 0, 1, … do
2:	$b^{k+1}={\text{prox}}_{t_k{J}_{\mathrm{\lambda }}}(a^k-t_k{X}^{\prime }(X{a}^k-y))$
3:	${\theta }_{k+1}^{-1}=\frac{1}{2}(1+\sqrt{1+4/{\theta }_k^2})$
4:	$a^{k+1}=b^{k+1}+{\theta }_{k+1}({\theta }_k^{-1}-1)(b^{k+1}-b^k)$
5:	end for

The code in our numerical experiments uses a straightforward implementation of the standard FISTA algorithm, along with problem-specific stopping criteria. Standalone Matlab and R implementations of the algorithm are available at http://www-stat.stanford.edu/~candes/SortedL1. In addition, the TFOCS package available at http://cvxr.com Becker, Candès and Grant (2011) implements Algorithms 1 and 2 as well as its many variants.

2.2. Fast prox algorithm

Given y ∈ ℝ^p and λ₁ ≥ λ₂ ≥ ⋯ ≥ λ_p ≥ 0, the prox to the sorted ℓ₁ norm is the unique solution to

$$\text{prox}(y;\mathrm{\lambda }):=\underset{x\in {ℝ}^p}{\text{arg}min}\frac{1}{2}{\Vert y-x\Vert }_{{\ell }_2}^2+{\displaystyle \sum _{i=1}^p{\mathrm{\lambda }}_i{|x|}_{(i)}}.$$ (2.2)

A simple observation is this: at the solution to (2.2), the sign of each x_i ≠ 0 will match that of y_i. It therefore suffices to solve the problem for $|y|$ and restore the signs in a post-processing step, if needed. Likewise, note that applying any permutation P to y results in a solution P x. We can thus choose a permutation that sorts the entries in y and apply its inverse to obtain the desired solution. Therefore, without loss of generality, we can make the following assumption:

ASSUMPTION 2.1

The vector y obeys y₁ ≥ y₂ ≥ ⋯ ≥ y_p ≥ 0.

The proposition below, proved in the supplementary Appendix [Bogdan et al. (2015)], provides a convenient reformulation of the proximal problem (2.2) by reformulating it as a quadratic program (QP).

PROPOSITION 2.2

Under Assumption 2.1 we can reformulate (2.2) as

$$\begin{array}{ll}\mathit{minimize}\hfill & \frac{1}{2}{\Vert y-x\Vert }_{{\ell }_2}^2+{\displaystyle \sum _{i=1}^p{\mathrm{\lambda }}_i{x}_i},\hfill \\ \mathit{subject to}\hfill & x_1\ge x_2\ge \cdots \ge x_p\ge 0.\hfill \end{array}$$ (2.3)

Algorithm 3 FastProxSL1

input: Nonnegative and nonincreasing sequences y and λ.

while y − λ is not nonincreasing do

Identify nondecreasing and nonconstant subsequences, that is, segments i : j such that $\begin{array}{lll}{y}_i-{\mathrm{\lambda }}_i\le y_{i+1}-{\mathrm{\lambda }}_{i+1}\le \cdots \le y_j-{\mathrm{\lambda }}_j\hfill & \text{and}\hfill & y_i-{\mathrm{\lambda }}_i<y_j-{\mathrm{\lambda }}_j.\hfill \end{array}$ (2.4)   Replace the values of y and λ over such segments by their average value: for k ∈ {i, i + 1, …, j} $\begin{array}{ll}{y}_k\leftarrow \frac{1}{j-i+1}{\displaystyle \sum _{i\le k\le j}{y}_k,}\hfill & {\mathrm{\lambda }}_k\leftarrow \frac{1}{j-i+1}{\displaystyle \sum _{i\le k\le j}{\mathrm{\lambda }}_k.}\hfill \end{array}$

end while

output: x = (y − λ)+.

We do not suggest performing the prox calculation by calling a standard QP solver applied to (2.3). Rather, we introduce the FastProxSL1 algorithm for computing the prox: for ease of exposition, we introduce Algorithm 3 in its simplest form before presenting a stack implementation (Algorithm 4) running in O (p) flops, after an O (p log p) sorting step.

Algorithm 3, which terminates in at most p steps, is simple to understand: we simply keep on averaging until the monotonicity property holds, at which point the solution is known in closed form. The key point establishing the correctness of the algorithm is that the update does not change the value of the prox. This is formalized below.

Algorithm 4 Stack-based algorithm for FastProxSL1
1:	input: Nonnegative and nonincreasing sequences y and λ.
2:	# Find optimal group levels
3:	t ← 0
4:	for k = 1 to n do
5:	t ← t + 1
6:	(i, j, s, w)t = (k, k, yi − λi, (yi − λi)+)
7:	while (t > 1) and (wt−1 ≤ wt) do
8:	${(i,j,s,w)}_{t-1}\leftarrow (i_{t-1},j_t,s_{t-1}+s_t,(\frac{j_{t-1}-i_{t-1}+1}{j_t-i_{t-1}+1}\cdot s_{t-1}+\frac{j_t-i_t+1}{j_t-i_{i-1}+1}\cdot s_t)+)$
9:	Delete (i, j, s, w)t, t ← t − 1
10:	end while
11:	end for
12:	# Set entries in x for each block
13:	for ℓ = 1 to t do
14:	for k = iℓ to jℓ do
15:	xk ← wℓ
16:	end for
17:	end for

LEMMA 2.3

The solution does not change after each update; formally, letting (y⁺, λ⁺) be the updated value of (y, λ) after one pass in Algorithm 3,

$$\text{prox}(y;\mathrm{\lambda })=\text{prox}(y^{+};{\mathrm{\lambda }}^{+}).$$

Next, if (y − λ)₊ is nonincreasing, then it is the solution to (2.2), that is, prox(y; λ) = (y − λ)₊.

This lemma, whose proof is in the supplementary Appendix [Bogdan et al. (2015)], guarantees that the FastProxSL1 algorithm finds the solution to (2.2) in a finite number of steps.

As stated earlier, it is possible to obtain a careful O(p) implementation of FastProxSL1. Below we present a stack-based approach. We use tuple notation (a, b)_i = (c, d) to denote a_i = c, b_i = d. For the complexity of the algorithm note that we create a total of p new tuples. Each of these tuples is merged into a previous tuple at most once. Since the merge takes a constant amount of time, the algorithm has the desired O(p) complexity.

With this paper, we are making available a C, a Matlab and an R implementation of the stack-based algorithm at http://www-stat.stanford.edu/~candes/SortedL1. The algorithm is also implemented in R package SLOPE, available on CRAN, and included in the current version of the TFOCS package. Table 1 reports the average runtimes of the algorithm (MacBook Pro, 2.66 GHz, Intel Core i7) when applied to vectors of fixed length and varying sparsity.

TABLE 1.

Average runtimes of the stack-based prox implementation with normalization steps (sorting and sign changes) included, respectively, excluded

	p = 105	p = 106	p = 107
Total prox time (s)	9.82e−03	1.11e−01	1.20e+00
Prox time after normalization (s)	6.57e−05	4.96e−05	5.21e−05

2.3. Related algorithms

Brad Efron informed us about the connection between the FastProxSL1 algorithm for SLOPE and a simple iterative algorithm for solving isotonic problems called the pool adjacent violators algorithm (PAVA) [Barlow et al. (1972), Kruskal (1964)]. A simple instance of an isotonic regression problem involves fitting data in a least-squares sense in such a way that the fitted values are monotone:

$$\begin{array}{ll}\text{minimize}\hfill & \frac{1}{2}{\Vert y-x\Vert }_{{\ell }_2}^2,\hfill \\ \text{subject to}\hfill & x_1\ge x_2\ge \cdots \ge x_p.\hfill \end{array}$$ (2.5)

Here, y is a vector of observations and x is the vector of fitted values, which are here constrained to be nonincreasing. We have chosen this formulation to emphasize the connection with (2.3). Indeed, our QP (2.3) is equivalent to

$$\begin{array}{ll}\text{minimize}\hfill & \frac{1}{2}{\displaystyle \sum _{i=1}^p{(y_i-{\mathrm{\lambda }}_i-x_i)}^2},\hfill \\ \text{subject to}\hfill & x_1\ge x_2\ge \cdots \ge x_p\ge 0,\hfill \end{array}$$

so that we see are really solving an isotonic regression problem with data y_i − λ_i. Algorithm 3 is then a version of PAVA as described in Barlow et al. (1972); see Best and Chakravarti (1990), Grotzinger and Witzgall (1984) for related work and connections with active set methods. Also, an elegant R package for isotone regression has been contributed by de Leeuw, Hornik and Mair (2009) and can be used to compute the prox to the sorted ℓ₁ norm.

Similar algorithms were also proposed in Zhong and Kwok (2012) to solve the OSCAR optimization problem defined as

$$\begin{array}{ll}\text{minimize}\hfill & \frac{1}{2}{\Vert y-Xb\Vert }_{{\ell }_2}^2+{\mathrm{\lambda }}_1{\Vert b\Vert }_{{\ell }_1}+{\mathrm{\lambda }}_2{\displaystyle \sum _{i<j}max(|b_i|,|b_j|)}.\hfill \end{array}$$ (2.6)

The OSCAR formulation was introduced in Bondell and Reich (2008) to encourage grouping of correlated predictors. The OSCAR penalty term can be expressed as ${\displaystyle {\sum }_{i=1}^p{\alpha }_i{|b|}_{\left(i\right)}}$ with α_i = λ₁ + (p − i)λ₂; hence, this is a sorted ℓ₁ norm with a linearly decaying sequence of weights. Bondell and Reich (2008) do not present a special algorithm for solving (2.6) other than casting the problem as a QP. In the article Zeng and Figueiredo (2014), which appeared after our manuscript was made publicly available, the OSCAR penalty term was further generalized to a Weigthed Sorted L-one norm, which coincides with the SLOPE formulation. This latter article does not discuss statistical properties of this fitting procedure.

3. Results

We now illustrate the performance of our SLOPE proposal in three different ways. First, we describe a multiple-testing situation where reducing the problem to a model selection setting and applying SLOPE assures FDR control, and results in a testing procedure with appreciable properties. Second, we discuss guiding principles to choose the sequence of λ_i’s in general settings, and illustrate the efficacy of the proposals with simulations. Third, we apply SLOPE to a data set collected in genetics investigations.

3.1. An application to multiple testing

In this section we show how SLOPE can be used as an effective multiple comparison controlling procedure in a testing problem with a specific correlation structure. Consider the following situation. Scientists perform p = 1000 experiments in each of 5 randomly selected laboratories, resulting in observations that can be modeled as

$$y_{i,j}={\mu }_i+{\tau }_j+z_{i,j},1\le i\le 1000,1\le j\le 5,$$ (3.1)

where the laboratory effects τ_j are i.i.d. $\mathcal{N}(0,{\sigma }_{\tau }^2)$ random variables and the errors z_i,j are i.i.d. $\mathcal{N}(0,{\sigma }_z^2)$, with the τ and z sequences independent of each other. It is of interest to test whether H_i : μ_i = 0 versus a two-sided alternative. Averaging the scores over all five labs results in

$${\overline{y}}_i={\mu }_i+\overline{\tau }+{\overline{z}}_i,1\le i\le 1000,$$

with $\overline{y}\sim \mathcal{N}\left(\mu ,\sum \right)$ and ${\sum }_{i,i}=\frac{1}{5}({\sigma }_{\tau }^2+{\sigma }_z^2)={\sigma }^2$ and ${\sum }_{i,i}=\frac{1}{5}{\sigma }_{\tau }^2=\rho$ for i ≠ j.

The problem has then been reduced to testing if the marginal means of a multivariate Gaussian vector with equicorrelated entries do not vanish. One possible approach is to use marginal tests based on ${\overline{y}}_i’\mathrm{s}$ and rely on the Benjamini–Hochberg procedure to control FDR. That is, we can order ${|\overline{y}|}_{\left(1\right)}\ge {|\overline{y}|}_{\left(2\right)}\ge \cdots \ge {|\overline{y}|}_{\left(p\right)}$ and apply the step-up procedure with critical values equal to $\sigma \cdot {\mathrm{\Phi }}^{-1}\left(1-iq/2p\right)$.

Another possible approach is to “whiten the noise” and express−our multiple testing problem in the form of a regression equation

$$\tilde{y}={\sum }^{-1/2}\overline{y}={\sum }^{-1/2}\mu +\epsilon ,$$ (3.2)

where $\epsilon \sim \mathcal{N}(0,I_p)$. Treating ${\sum }^{-1/2}$ as the regression design matrix, our problem is equivalent to classical model selection: identify the nonzero components of the vector μ of regression coefficients.¹⁰ Note that while the matrix is far from being diagonal, ${\sum }^{-1/2}$ is diagonally dominant. For example, when σ² = 1 and ρ = 0.5, then ${\sum }_{i,i}^{-1/2}=1.4128$ and ${\sum }_{i,j}^{-1/2}=-0.0014$ for i ≠ j. Thus, every low-dimensional submodel obtained by selecting few columns of the design matrix ${\sum }^{-1/2}$ will be very close to orthogonal. In summary, the transformation (3.2) reduces the multiple-testing problem with strongly positively correlated test statistics to a problem of model selection under approximately orthogonal design, which is well suited for the application of SLOPE with the λ_BH values.

To compare the performances of these two approaches, we simulate data according to the model (3.1) with variance components ${\sigma }_{\tau }^2={\sigma }_z^2=2.5$, which yield σ² = 1 and ρ = 0.5. We consider a sequence of sparse settings, where the number k of nonzero μ_i’s varies between 0 and 80. To obtain moderate power, the nonzero means are set to $\sqrt{2\text{log}p}/c\approx 2.63$, where c is the Euclidean norm of each of the columns of ${\sum }^{-1/2}$. We compare the performance of SLOPE and BH on marginal tests under two scenarios: (1) assuming ${\sigma }_{\tau }^2={\sigma }_z^2=2.5$ known, and (2) estimating them using the classical unweighted means method based on equating the ANOVA mean squares to their expectations:

$${\widehat{\sigma }}_z^2=\text{MSE},{\widehat{\sigma }}_{\tau }^2=\frac{\text{MS}\tau -\text{MSE}}{1000};$$

using the standard notation from ANOVA analysis, MSE is the mean square due to the error in the model (3.1) and MSτ is the mean square due to the random factor τ. To use SLOPE, we center the vector $\tilde{y}$ by subtracting its mean, and center and standardize the columns of ${\widehat{\sum }}^{-1/2}$, so they have zero means and unit l₂ norms. Figure 3 reports the results of these simulations, averaged over 500 independent replicates.

FIG. 3.

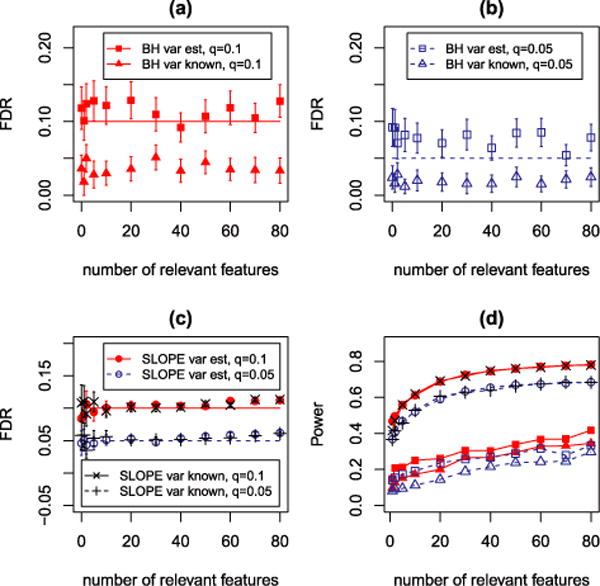
Simulation results for testing multiple means from correlated statistics. (a)–(b) Mean FDP ± 2 SE for marginal tests as a function of k. (c) Mean FDP ± 2 SE for SLOPE. (d) Power plot.

In our setting, the estimation procedure has no influence on SLOPE. Under both scenarios (variance components known and unknown) SLOPE keeps FDR at the nominal level as long as k ≤ 40. Then its FDR slowly increases, but for k ≤ 80 it is still very close to the nominal level as shown in Figure 3(c). In contrast, the performance of BH differs significantly: when σ² is known, BH on the marginal tests is too conservative, with an average FDP below the nominal level; see Figure 3(a) and (b). When σ² is estimated, the average FDP of this procedure increases and for q = 0.05, it significantly exceeds the nominal level. Under both scenarios (known and unknown σ²) the power of BH is substantially smaller than the power provided by SLOPE [Figure 3(d)]. Moreover, the False Discovery Proportion (FDP) in the marginal tests with BH correction appears more variable across replicates than that of SLOPE [Figure 3(a), (b) and (c)]. Figure 4 presents the results in greater detail for q = 0.1 and k = 50: in approximately 65% of the cases the observed FDP for BH is equal to 0, while in the remaining 35% it takes values which are distributed over the whole interval (0, 1). This behavior is undesirable. On the one hand, FDP = 0 typically equates with few discoveries (and hence power loss). On the other hand, if many FDP = 0 contribute to the average in the FDR, this quantity is kept below the desired level q even if, when there are discoveries, a large number of them are false. Indeed, in approximately 26% of all cases BH on the marginal tests did not make any rejections (i.e., R = 0); and conditional on R > 0, the mean of FDP is equal to 0.16 with a standard deviation of 0.28, which clearly shows that the observed FDP is typically far away from the nominal value of q = 0.1. In other words, while BH is close to controlling the FDR, the scientists would either make no discoveries or have very little confidence on those actually made. In contrast, SLOPE results in a more predictable FDP and a substantially larger and more predictable True Positive Proportion (TPP, fraction of correctly identified true signals); see Figure 4.

FIG. 4.

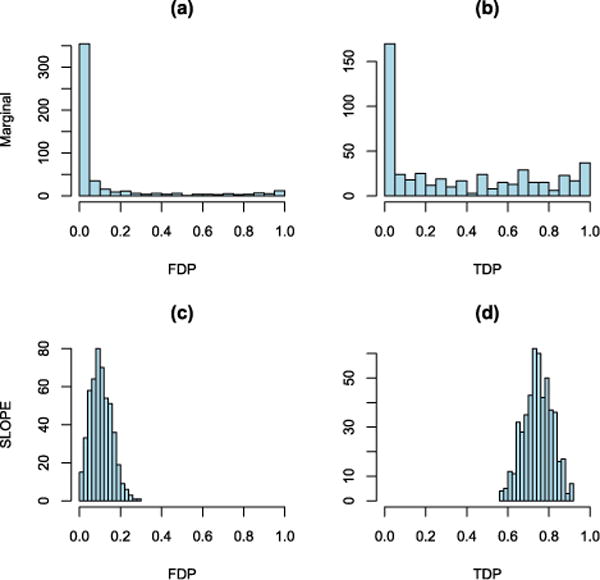
Testing example with q = 0.1 and k = 50. The top row refers to marginal tests, and the bottom row to SLOPE. Both procedures use the estimated variance components. Histograms of false discovery proportions are in the first column and of true positive proportions in the second.

3.2. Choosing λ in general settings

In the previous sections we observed that, for orthogonal designs, Lasso with λ_Bonf = σ · Φ⁻¹(1 − α/2p) controls FWER at the level α, while SLOPE with the sequence λ = λ_BH controls FDR at the level q. We are interested, however, in applying these procedures in more general settings, specifically when p > n and there is some correlation among the explanatory variables, and when the value of σ² is not known. We start tackling the first situation. Correlation among regressors notoriously introduces a series of complications in the statistical analysis of linear models, ranging from the increased computational costs that motivated the early popularity of orthogonal designs, to the conceptual difficulties of distinguishing causal variables among correlated ones. Indeed, recent results on the consistency of ℓ₁ penalization methods typically require some form of partial orthogonality. SLOPE and Lasso aim at finite sample properties, but it would not be surprising if departures from orthogonality were to have a serious effect. To explore this, we study the performance of Lasso and SLOPE in the case where the entries of the design matrix are generated independently from the $\mathcal{N}\left(0,1/n\right)$ distribution. Specifically, we consider two Gaussian designs with n = 5000: one with p = 2n = 10,000 and one with p = n/2 = 2500. We set the value of nonzero coefficients to $5\sqrt{2\text{log}p}$ and consider situations where the number of important variables ranges between 0 and 100. Figure 5 illustrates that under such Gaussian designs both Lasso–λ_Bonf and SLOPE lose the control over their targeted error rates (FWER and FDR) as the number k of nonzero coefficients increases, with a departure that is more severe when the ratio between p/n is larger.

FIG. 5.

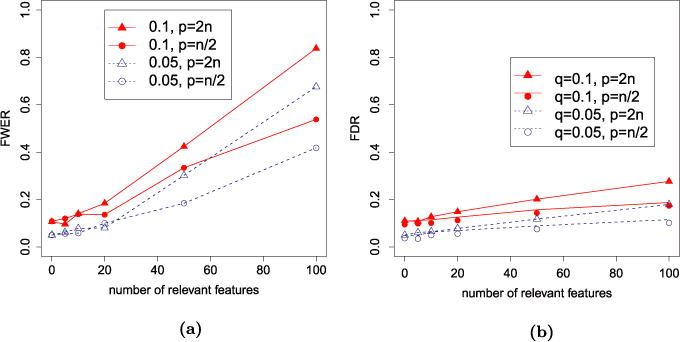
Observed (a) FWER for Lasso with λ_Bonf and (b) FDR for SLOPE with λ_BH under Gaussian design and n = 5000. The results are averaged over 500 replicates.

3.2.1. The effect of shrinkage

What is behind this fairly strong effect, and is it possible to choose a λ sequence to compensate it? Some useful insights come from studying the solution of the Lasso. Assume that the columns of X have unit norm and that $z\sim \mathcal{N}\left(0,1\right)$. Then the optimality conditions for the Lasso give

$$\begin{array}{l}\widehat{\beta }={\eta }_{\mathrm{\lambda }}\left(\widehat{\beta }-X^{\prime }\left(X\widehat{\beta }-y\right)\right)={\eta }_{\mathrm{\lambda }}\left(\widehat{\beta }-X^{\prime }\left(X\widehat{\beta }-X\beta -z\right)\right)\\ ={\eta }_{\mathrm{\lambda }}\left(\widehat{\beta }-X^{\prime }X\left(\widehat{\beta }-\beta \right)+X^{\prime }z\right),\end{array}$$ (3.3)

where η_λ is the soft-thresholding operator, ${\eta }_{\mathrm{\lambda }}(t)=\text{sgn}(t){\left(|t|-\mathrm{\lambda }\right)}_{+}$, applied componentwise. Defining $v_i=\langle X_i,{\displaystyle {\sum }_{j\ne i}{X}_j({\beta }_j-{\widehat{\beta }}_j)}\rangle$, we can write

${\widehat{\beta }}_i={\eta }_{\mathrm{\lambda }}({\beta }_i+X_i^{\prime }z+v_i),$ (3.4)

which expresses the relation between the estimated value of ${\widehat{\beta }}_i$ and its true value β_i. If the variables are orthogonal, the v_i’s are identically equal to 0, leading to ${\widehat{\beta }}_i={\eta }_{\mathrm{\lambda }}({\beta }_i+X_i^{\prime }z)$. Conditionally on X, $X_i^{\prime }z\sim \mathcal{N}\left(0,1\right)$ and by using Bonferroni’s method, one can choose λ such that $\mathbb{P}({max}_i|X_i^{\prime }z|>\mathrm{\lambda })\le \alpha$. When X is not orthogonal, however, v_i ≠ 0 and its size increases with the estimation error of β_j (for i ≠ j)—which depends on the magnitude of the shrinkage parameter λ. Therefore, even in the perfect situation where all the k relevant variables, and those alone, have been selected, and when all columns of the design matrix are realizations of independent random variables, v_i will not be zero. Rather, the squared magnitude $v_i^2$ will be on the order of λ² · k/n. In other words, the variance that would determine the correct Bonferroni threshold is on the order 1 + λ² k/n. In reality, the true k is not known a priori, and the selected k depends on the value of the smoothing parameter λ, so that it is not trivial to implement this correction in the Lasso. SLOPE, however, uses a decreasing sequence λ, analogous to a step-down procedure, and this extra noise due to the shrinkage of relevant variables can be incorporated by progressively modifying the λ sequence. In evocative, if not exact terms, λ₁ is used to select the first variable to enter the model: at this stage we are not aware of any variable whose shrunk coefficient is “effectively increasing” the noise level, and we can keep λ₁ = λ_BH(1). The value of λ₂ determines the second variable to enter the model and, hence, we know that there is already one important variable whose coefficient has been shrunk by roughly λ_BH(1); we can use this information to redefine λ₂. Similarly, when using λ₃ to identify the third variable, we know of two relevant regressors whose coefficients have been shrunk by amounts determined by λ₁ and λ₂, and so on. What follows is an attempt to make this intuition more precise, accounting for the fact that the sequence λ needs to be determined a priori, and we need to make a prediction on the values of the cross products $X_i^{\prime }{X}_j$ appearing in the definition of v_i. Before we turn to this, we want to underscore how this explanation for the loss of FDR control is consistent with patterns evident from Figure 5: the problem is more serious as k increases (and, hence, the effect of shrinkage is felt on a larger number of variables) and as the ratio p/n increases (which for Gaussian designs results in larger empirical correlation $|X_i^{\prime }{X}_j|$). Our loose analysis suggests that when k is really small, SLOPE with λ_BH yields an FDR that is close to the nominal level, as empirically observed.

3.2.2. Adjusting the regularizing sequence for SLOPE

In light of (3.4), we would like an expression for $X_i^{\prime }{X}_{\mathcal{S}}({\beta }_{\mathcal{S}}-{\widehat{\beta }}_{\mathcal{S}})$, where with $\mathcal{S}$, $X_{\mathcal{S}}$ and ${\beta }_{\mathcal{S}}$ we indicate the support of β, the subset of variables associated to β_i ≠ 0, and the value of their coefficients, respectively.

Again, to obtain a very rough evaluation of the SLOPE solution, we can start from the Lasso. Let us assume that the size of β_S and the value of λ are such that the support and the signs of the regression coefficients are correctly recovered in the solution. That is, we assume that $\text{sign}({\beta }_j)=\text{sign}({\widehat{\beta }}_j)$ for all j, with the convention that sign(0) = 0. Without loss of generality, we further assume that β_j ≥ 0. Now, the Karush–Kuhn–Tucker (KKT) optimality conditions for the Lasso yield

$$X_S^{\prime }(y-X{\widehat{\beta }}_S)=\mathrm{\lambda }\cdot 1_S,$$ (3.5)

implying

$${\widehat{\beta }}_S={(X_S^{\prime }{X}_S)}^{-1}(X_S^{\prime }y-\mathrm{\lambda }\cdot 1_S).$$

In the case of SLOPE, rather than one λ, we have a sequence λ₁, …, λ_p. Assuming again that this is chosen so that we recover exactly the support $\mathcal{S}$, the estimates of the nonzero components are very roughly equal to

$${\widehat{\beta }}_S={(X_{\mathcal{S}}^{\prime }{X}_{\mathcal{S}})}^{-1}(X_{\mathcal{S}}^{\prime }y-{\mathrm{\lambda }}_{\mathcal{S}})={\widehat{\beta }}_{\text{OLS}}-{(X_{\mathcal{S}}^{\prime }{X}_{\mathcal{S}})}^{-1}{\mathrm{\lambda }}_{\mathcal{S}},$$

where ${\mathrm{\lambda }}_{\mathcal{S}}={({\mathrm{\lambda }}_1,\dots ,{\mathrm{\lambda }}_{|S|})}^{\prime }$ and ${\widehat{\beta }}_{\text{OLS}}$ is the least-squares estimator of β_S. This leads to $\mathbb{E}({\beta }_{\mathcal{S}}-{\widehat{\beta }}_S)\approx \theta {(X_{\mathcal{S}}^{\prime }{X}_{\mathcal{S}})}^{-1}{\mathrm{\lambda }}_{\mathcal{S}}$ and

$$\mathbb{E}{X}_i^{\prime }{X}_{\mathcal{S}}({\beta }_{\mathcal{S}}-{\widehat{\beta }}_{\mathcal{S}})\approx \mathbb{E}{X}_i^{\prime }{X}_{\mathcal{S}}{(X_{\mathcal{S}}^{\prime }{X}_{\mathcal{S}})}^{-1}{\mathrm{\lambda }}_{\mathcal{S}},$$

an expression that tells us the typical size of v_i in (3.4).

For the case of Gaussian designs, where the entries of X are i.i.d. $\mathcal{N}\left(0,1/n\right)$, for $i\notin \mathcal{S}$,

$$\begin{array}{c}\mathbb{E}{(X_i^{\prime }{X}_{\mathcal{S}}{(X_{\mathcal{S}}^{\prime }{X}_{\mathcal{S}})}^{-1}{\mathrm{\lambda }}_{\mathcal{S}})}^2=\frac{1}{n}{{\mathrm{\lambda }}^{\prime }}_{\mathcal{S}}\mathbb{E}{(X_{\mathcal{S}}^{\prime }{X}_{\mathcal{S}})}^{-1}{\mathrm{\lambda }}_{\mathcal{S}}=w(|\mathcal{S}|)\cdot {\Vert {\mathrm{\lambda }}_{\mathcal{S}}\Vert }_{{\ell }_2}^2,\\ w(k)=\frac{1}{n-k-1}.\end{array}$$ (3.6)

This uses the fact that the expected value of an inverse k×k Wishart with n degrees of freedom is equal to I^k/(n − k − 1).

This suggests the sequence of λ’s described below denoted by λ_G since it is motivated by Gaussian designs. We start with λ_G(1) = λ_BH(1). At the next stage, however, we need to account for the slight increase in variance so that we do not want to use λ_BH(2) but rather

$${\mathrm{\lambda }}_{\mathrm{G}}(2)={\mathrm{\lambda }}_{\text{BH}}(2)\sqrt{1+w(1){\mathrm{\lambda }}_{\mathrm{G}}{(1)}^2}.$$

Continuing, this gives

$${\mathrm{\lambda }}_{\mathrm{G}}(i)={\mathrm{\lambda }}_{\text{BH}}(i)\sqrt{1+w(i-1){\displaystyle \sum _{j<i}{\mathrm{\lambda }}_{\mathrm{G}}{(j)}^2}}.$$ (3.7)

Figure 6 plots the adjusted values given by (3.7). As is clear, these new values yield a procedure that is more conservative than that based on λ_BH. It can be observed that the corrected sequence λ_G(i) may no longer be decreasing (as in the case where n = p/2 in the figure). It would not make sense to use such a sequence—note that SLOPE would no longer be convex—and letting k^⋆ = k(n, p, q) be the location of the global minimum, we shall work with

$${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}(i)=\{\begin{array}{ll}{\mathrm{\lambda }}_{\mathrm{G}}(i),\hfill & i\le k^{\star },\hfill \\ {\mathrm{\lambda }}_{k^{\star }},\hfill & i>k^{\star },\hfill \end{array}\text{with}{\mathrm{\lambda }}_{\mathrm{G}}(i)\text{as in}(3.7).$$ (3.8)

FIG. 6.

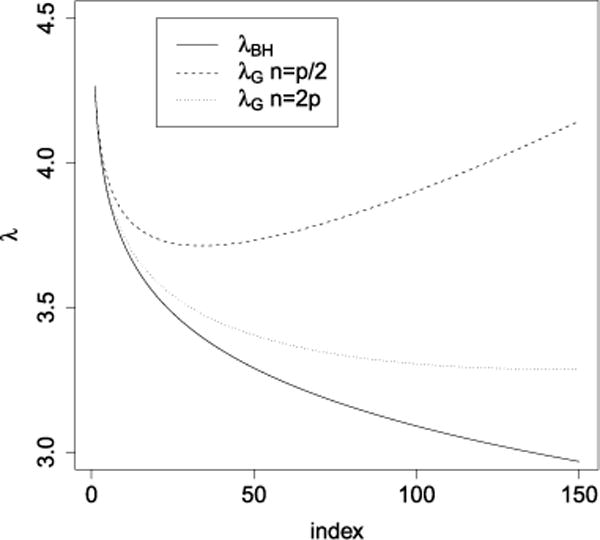
Graphical representation of sequences {λ_i} for p = 5000 and q = 0.1. The solid line is λ_BH, the dashed (resp., dotted) line is λ_G given by (3.7) for n = p/2 (resp., n = 2p).

An immediate validation—if the intuition that we have stretched this far has any bearing in reality—is the performance of ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ in the setup of Figure 5. In Figure 7 we illustrate the performance of SLOPE for large signals ${\beta }_i=5\sqrt{2\text{log}p}$ as in Figure 5, as well as for rather weak signals with ${\beta }_i=\sqrt{2\text{log}p}$. The correction works very well, rectifying the loss of FDR control documented in Figure 5. For p = 2n = 10,000, the values of the critical point k^⋆ are 51 for q = 0.05 and 68 for q = 0.1. For p = n/2 = 2500, they become 95 and 147, respectively. It can be observed that for large signals, SLOPE keeps FDR below the nominal level even after passing the critical point. Interestingly, the control of FDR is more difficult when the coefficients have small amplitudes. We believe that some increase of FDR for weak signals is related to the loss of power, which our correction does not account for. However, even for weak signals the observed FDR of SLOPE with ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ is very close to the nominal level when k ≤ k^⋆.

FIG. 7.

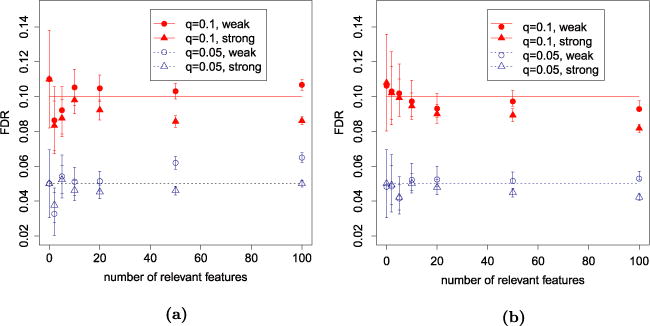
Mean FDP ± 2 SE for SLOPE with ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$. Strong signals have nonzero regression coefficients set to $5\sqrt{2\text{log}p}$, while this value is set to $\sqrt{2\text{log}p}$ for weak signals. (a) p = 2n = 10,000. (b) p = n/2 = 2500.

In situations where one cannot assume that the design is Gaussian or that columns are independent, we suggest replacing $w(i-1){\displaystyle {\sum }_{j<i}{\mathrm{\lambda }}_j^2}$ in the formula (3.7) with a Monte Carlo estimate of the correction. Let X denote the standardized version of the design matrix, so that each column has a mean equal to zero and unit l₂ norm. Suppose we have computed λ₁, …, λ_i−1 and wish to compute λ_i. Let X_S indicate a matrix formed by selecting those columns with indices in some set $\mathcal{S}$ of cardinality i − 1 and let $j\notin \mathcal{S}$. After randomly selecting $\mathcal{S}$ and j, the correction approximated by the average of ${(X_j^{\prime }{X}_{\mathcal{S}}{(X_{\mathcal{S}}^{\prime }{X}_{\mathcal{S}})}^{-1}{\mathrm{\lambda }}_{1:i-1})}^2$ across realizations, where ${\mathrm{\lambda }}_{1:i-1}={\left({\mathrm{\lambda }}_1,\dots {,\mathrm{\lambda }}_{i-1}\right)}^{\prime }$.

Significantly more research is needed to understand the properties of this heuristic and to design more efficient alternatives. Our simulations so far suggest that it provides approximate FDR control when looking at the average across all possible signal placements, and—for any fixed signal location—if the columns of the design matrix are exchangeable. It is important to note that the computational cost of this procedure is relatively low. Two elements contribute to this. First, the complexity of the procedure is reduced by the fact that the sequence of λ’s does not need to be estimated entirely, but only up to the point k^⋆ where it starts increasing (or simply flattens) and only for a number of entries on the order of the expected number of nonzero coefficients. Second, the smoothness of λ assures that it is enough to estimate λ on a grid of points between 1 and k^⋆, making the problem tractable also for very large p. In Bogdan et al. (2013) we applied a similar procedure for the estimation of the regularizing sequence with p = 2048² = 4,194,304 and n = p/5 and found out that it was sufficient to estimate this sequence at only 40 grid points.

3.2.3. Unknown σ

According to formulas (1.5) and (1.10), the penalty in SLOPE depends on the standard deviation σ of the error term. In many applications σ is not known and needs to be estimated. When n is larger than p, this can easily be done by means of classical unbiased estimators. When p ≥ n, some solutions for simultaneous estimation of σ and regression coefficients using ℓ₁ optimization schemes were proposed; see, for example, Städler, Bühlmann and van de Geer (2010) and Sun and Zhang (2012). Specifically, Sun and Zhang (2012) introduced a simple iterative version of the Lasso called the scaled Lasso. The idea of this algorithm can be applied to SLOPE, with some modifications. For one, our simulation results show that, under very sparse scenarios, it is better to de-bias the estimates of regression parameters by using classical least-squares estimates within the selected model to obtain an estimate of σ².

Algorithm 5 Iterative SLOPE fitting when σ is unknown
1:	input: y, X and initial sequence λS (computed for σ = 1)
2:	initialize: S+ = ∅
3:	repeat
4:	S = S+
5:	compute the RSS obtained by regressing y onto variables in S
6:	set ${\widehat{\sigma }}^2=\text{RSS}/\left(n-|S|-1\right)$
7:	compute the solution $\widehat{\beta }$ to SLOPE with parameter sequence $\widehat{\sigma }\cdot {\mathrm{\lambda }}^S$
8:	set $S_{+}=\text{supp}\left(\widehat{\beta }\right)$
9:	until S+ = S

We present our algorithm above (Algorithm 5). There, λ^S is the sequence of SLOPE parameters designed to work with σ = 1, obtained using the methods from Section 3.2.2.

The procedure starts by using a conservative estimate of the standard deviation of the error term ${\widehat{\sigma }}^{\left(0\right)}=\text{Std}\left(y\right)$ and a related conservative version of SLOPE with ${\mathrm{\lambda }}^{\left(0\right)}={\widehat{\sigma }}^{\left(0\right)}\cdot {\mathrm{\lambda }}^S$. Then, in consecutive runs ${\widehat{\sigma }}^{\left(k\right)}$ is computed using residuals from the regression model, which includes variables identified by SLOPE with sequence σ^(k−1) · λ^S. The procedure is repeated until convergence, that is, until the next iteration results in exactly the same model as the current one.

3.2.4. Simulations with idealized GWAS data

We illustrate the performance of the “scaled” version of SLOPE and of our algorithm for the estimation of the parameters λ_i with simulations designed to mimic an idealized version of Genome Wide Association Studies (GWAS). We set n = p = 5000, and simulate 5000 genotypes of p independent Single Nucleotide Polymorphisms (SNPs). For each of these SNPs the minor allele frequency (MAF) is sampled from the uniform distribution on the interval (0.1, 0.5). Let us underscore that this assumption of independence is not met in actual GWAS, where the number of typed SNPs is in the order of millions. Rather, one can consider our data-generating mechanism as an approximation of the result of preliminary screening of genotype variants to avoid complications due to correlation. Our goal here is not to argue that SLOPE has superior performance in GWAS, but rather to illustrate the computational costs and inferential results of our algorithms. The explanatory variables are defined as

$${\tilde{x}}_{ij}=\{\begin{array}{ll}-1,\hfill & \text{for}aa,\hfill \\ 0,\hfill & \text{for}aA,\hfill \\ 1,\hfill & \text{for}AA,\hfill \end{array}$$ (3.9)

where a and A denote the minor and reference alleles at the jth SNP for the ith individual. Then the matrix $\tilde{X}$ is centered and standardized, so the columns of the final design matrix X have zero mean and unit norm. The trait values are simulated according to the model

$y=X\beta +z,$ (3.10)

where z ~ N(0, I), that is, we assume only additive effects and no interaction between loci (epistasis). We vary the number of nonzero regression coefficients k between 0 and 50 and we set their size to $1.2\sqrt{2\text{log}p}\approx 4.95$ (“moderate” signal). For each value of k, 500 replicates are performed, in each selecting randomly among the columns of X, the k with nonzero coefficients. Since our design matrix is centered and does not contain an intercept, we also center the vector of responses and let SLOPE work with $\tilde{y}=y-\overline{y}$, where $\overline{y}$ is the of y.

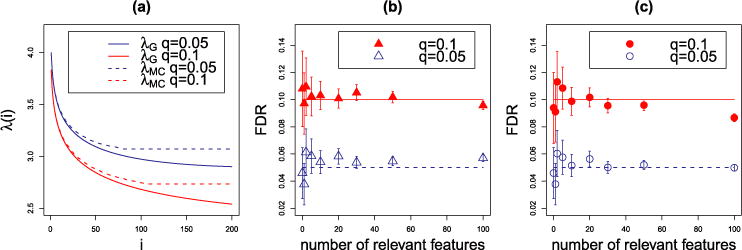
We set q = 0.05 and estimate the sequence λ via the Monte Carlo approach described in Section 3.2.2; here, we use 5000 independent random draws of X_S and X_j to compute the next term in the sequence. The calculations terminated in about 90 seconds (HP EliteDesk 800 G1 TWR, 3.40 GHz, Intel i7-4770) at λ₃₁, where the estimated sequence λ obtained a first local minimum. Figure 8(a) illustrates that up to this first minimum the Monte Carlo sequence λ_MC coincides with the heuristic sequence ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ for Gaussian matrices. In the result the FDR and power of “scaled” SLOPE are almost the same for both sequences [Figure 8(b) and (c)].

FIG. 8.

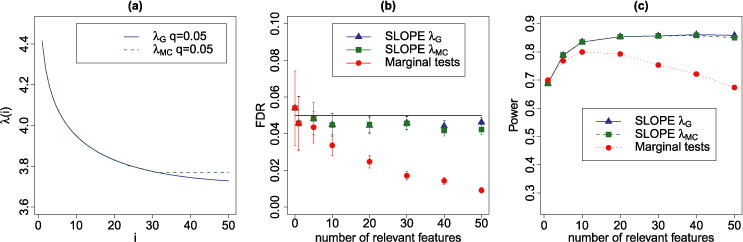
(a) Graphical representation of sequences λ_MC and λ_G for the SNP design matrix. (b) Mean FDP ± 2 SE for SLOPE with ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ and λ_MC and for BH as applied to marginal tests. (c) Power of both versions of SLOPE and BH on marginal tests for ${\beta }_1=\cdots ={\beta }_k=1.2\sqrt{2\text{log}p}\approx 4.95,\sigma =1$. In each replicate, the signals are randomly placed over the columns of the design matrix, and the plotted data points are averages over 500 replicates.

In our simulations, the proposed algorithm for scaled SLOPE converges very quickly. The conservative initial estimate of σ leads to a relatively small model with few false discoveries since σ⁽⁰⁾ · λ^S controls the FDR in sparse settings. Typically, iterations to convergence see the estimated value of σ decrease and the number of selected variables increase. Since some signals remain undetected (the power is usually below 100%), σ is slightly overestimated at the point of convergence, which translates into controlling the FDR at a level slightly below the nominal one; see Figure 8(b).

Figure 8(b) and (c) compare scaled SLOPE with the “marginal” tests. The latter are based on t-test statistics

$$t_i={{\widehat{\beta }}_i/\widehat{\sigma }}^2,{\widehat{\sigma }}^2={\text{RSS}}_i/(n-2),$$

where ${\widehat{\beta }}_i$ (resp., RSS_i) is the least-square estimate of the regression coefficient (resp., the residual sum of squares) in the simple linear regression model including only the ith SNP. To adjust for multiplicity, we use BH at the nominal FDR level q = 0.05.

It can be observed that SLOPE and marginal tests do not differ substantially when k ≤ 5. However, for k ≥ 10 the FDR of the marginal tests approach falls below the nominal level and the power decreases from 80% for k = 10 to 67% for k = 50. SLOPE’s power remains, instead, stable at the level of approximately 86% for k ∈ {20, …, 50}. This conservative behavior of marginal tests results from the inflation of the noise level estimate caused by regressors that are unaccounted for in the simple regression model.

We use this idealized GWAS setting to also explore the effect of some model misspecification. First, we consider a trait y on which genotypes have effects that are not simply additive. We formalize this via the matrix $\tilde{Z}$ collecting the “dominant” effects

$${\tilde{Z}}_{ij}=\{\begin{array}{ll}-1,\hfill & \text{for}aa,AA,\hfill \\ 1,\hfill & \text{for}aA.\hfill \end{array}$$ (3.11)

The final design matrix [X, Z] has the columns $[\tilde{X},\tilde{Z}]$ centered and standardized. Now the trait values are simulated according to the model

$$y=[X,Z]{\left[{\beta }_X^{\prime },{\beta }_Z^{\prime }\right]}^{\prime }+\epsilon ,$$

where ε ~ N(0, I), the number of “causal” SNPs k varies between 0 and 50, each causal SNP has an additive effect (nonzero components of β_X) equal to $1.2\sqrt{2\text{log}p}\approx 4.95$ and a dominant effect (nonzero components of β_Z) randomly sampled from $N(0,\sigma =2\sqrt{2\text{log}p})$. The data is analyzed using model (3.10), that is, assuming linear effect of alleles even when this is not true.

Second, to explore the sensitivity to violations of the assumption of the normality of the error terms, we considered (1) error terms z_i with a Laplace distribution and a scale parameter adjusted to that the variance is equal to one, and (2) error terms contaminated with 50 outliers ~ N(0, σ = 5) representing 1% of all observations.

Figure 9 summarizes the performance of SLOPE and of the marginal tests (adjusted for multiplicity via BH), which we include for reference purposes. Violation of model assumption appears to affect power rather than FDR in the case of SLOPE. Specifically, in all three examples FDR is kept very close to the nominal level while the power is somewhat diminished with respect to Figure 8. The smallest difference is observed in the case of Laplace errors, where the results of SLOPE are almost the same as in the case of normal errors. This is also the case where the difference in performance due to model misspecification is negligible for marginal tests. In all other cases, this approach seems to be much more sensitive than SLOPE to model misspecification.

FIG. 9.

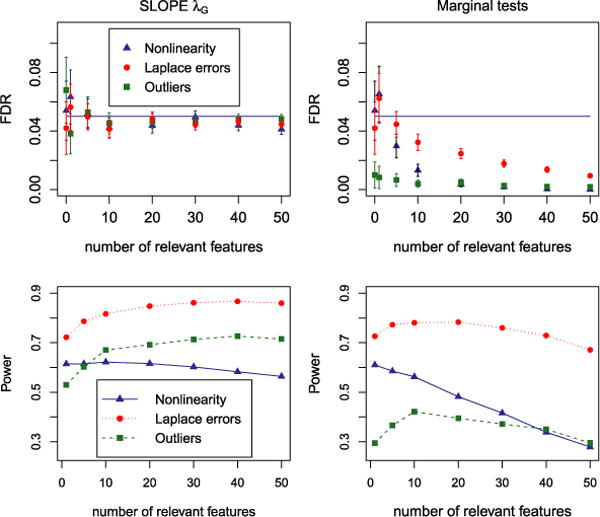
FDR and power of “scaled” SLOPE based on “gaussian” sequence ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ (left panel) and BH-corrected single marker tests (right panel) for different deviations from the assumed regression model. Error bars for FDR correspond to mean FDP ± 2 SE.

3.3. A real data example from genetics

In this section we illustrate the application of SLOPE to a current problem in genetics. In Service et al. (2014), the authors investigate the role of genetic variants in 17 regions in the genome, selected on the basis of previously reported association with traits related to cardiovascular health. Polymorphisms are identified via exome resequencing in approximately 6000 individuals of Finnish descent: this provides a comprehensive survey of the genetic diversity in the coding portions of these regions and affords the opportunity to investigate which of these variants have an effect on the traits of interest. While the original study has a broader scope, we here tackle the problem of identifying which genetic variants in these regions impact the fasting blood HDL levels. Previous literature reported associations between 9 of the 17 regions and HDL, but the resolution of these earlier studies was unable to pinpoint to specific variants in these regions or to distinguish if only one or multiple variants within the regions impact HDL. The resequencing study was designed to address this problem.

The analysis in Service et al. (2014) relies substantially on “marginal” tests: the effect of each variant on HDL is examined via a linear regression that has cholesterol level as outcome and the genotype of the variant as explanatory variable, together with covariates that capture possible population stratification. Such marginal tests are common in genetics and represent the standard approach in genome-wide association studies (GWAS). Among their advantages, it is worth mentioning that they allow to use all available observations for each variant without requiring imputation of missing data; their computational cost is minimal; and they result in a p-value for each variant that can be used to clearly communicate to the scientific community the strength of the evidence in favor of its impact on a particular trait. Marginal tests, however, cannot distinguish if the association between a variant and a phenotype is “direct” or due to correlation between the variant in question and another, truly linked to the phenotype. Since most of the correlation between genetic variants is due to their location along the genome (with nearby variants often correlated), this confounding is often considered not too serious a limitation in GWAS: multiple polymorphisms associated to a phenotype in one locus simply indicate that there is at least one genetic variant (most likely not measured in the study) with impact on the phenotype in the locus. The situation is quite different in the resequencing study we want to analyze, where establishing if one or more variants in the same region influence HDL is one of the goals. To address this, the authors of Service et al. (2014) resort to regressions that include two variables at the time: one of these being the variant with previously documented strongest marginal signal in the region, the other being variants that passed an FDR controlling threshold in the single variant analysis. Model selection strategies were only cursorily explored with a step-wise search routine that targets BIC. Such limited foray into model selection is motivated by the fact that one major concern in genetics is to control some global measure of type I error, and currently available model selection strategies do not offer finite sample guarantees with this regard. This goal is in line with that of SLOPE and so it is interesting for us to apply this new procedure to this problem.

The data set in Service et al. (2014) comprises 1878 variants, on 6121 subjects. Before analyzing it with SLOPE, or other model selection tools, we performed the following filtering. We eliminated from considerations variants observed only once (a total of 486), since it would not be possible to make inference on their effect without strong assumptions. We examined correlation between variants and selected for analysis a set of variants with pair-wise correlation smaller than 0.3. Larger values would make it quite challenging to interpret the outcomes; they render difficult the comparison of results across procedures since these might select different variables from a group of correlated ones; and large correlations are likely to adversely impact the efficacy of any model selection procedure. This reduction was carried out in an iterative fashion, selecting representatives from groups of correlated variables, starting from stronger levels of correlation and moving onto lower ones. Among correlated variables, we selected those that had stronger univariate association with HDL, larger minor allele frequency (diversity), and, among very rare variants, we privileged those whose annotation was more indicative of possible functional effects. Once variables were identified, we eliminated subjects that were missing values for more than 10 variants and for HDL. The remaining missing values were imputed using the average allele count per variant. This resulted in a design with 5375 subjects and 777 variants. The minor allele frequency of the variants included ranges from 2 × 10⁻⁴ to 0.5, with a median of 0.001 and a mean of 0.028: the data set still includes a number of rare variants, with the minor allele frequency smaller than 0.01.

In Service et al. (2014), association between HDL and polymorphisms was analyzed only for variants in regions previously identified as having an influence on HDL: ABCA1, APOA1, CEPT, FADS1, GALNT2, LIPC, LPL, MADD, and MVK (regions are identified with the name of one of the genes they contain). Moreover, only variants with minor allele frequencies larger than 0.01 were individually investigated, while nonsynonimous rare variants were analyzed with “burden tests.” These restrictions were motivated, at least in part, by the desire to reduce tests to the most well-powered ones, so that controlling for multiple comparisons would not translate in an excessive decrease of power. Our analysis is based on all variants that survive the described filtering in all regions, including those not directly sequenced in the experiment in Service et al. (2014), but included in the study as landmarks of previously documented associations (array SNPs in the terminology of the paper). We compare the following approaches: the (1) marginal tests described above in conjunction with BH and q = 0.05; (2) BH and q = 0.05 applied to the p-values from the full model regression; (3) Lasso with λ_Bonf and α = 0.05; (4) Lasso with λ_CV (in these last two cases we use the routines implemented in glmnet in R); (5) the R routine Step.AIC in forward direction and BIC as optimality criteria; (6) the R routine Step.AIC in backward direction and BIC as optimality criteria; (7) SLOPE with ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ and q = 0.05; (8) SLOPE with λ obtained via Monte Carlo starting from our design matrix. Defining the λ for Lasso–λ_Bonf and SLOPE requires a knowledge of the noise level σ²; we estimated this from the residuals of the full model. When estimating λ via the Monte Carlo approach, for each i we used 5000 independent random draws of X_S and X_j. Figure 10(a) illustrates that the Monte Carlo sequence λ_MC is only slightly larger than ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$: the difference increases with the index i, and becomes substantial for ranges of i that are unlikely to be relevant in the scientific problem at hand.

FIG. 10.

(a) Graphical representation of sequences λ_MC and λ_G for the variants design matrix. Mean FDP ± 2 SE for SLOPE with (b) ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ and (c) λ_MC and for the variants design matrix and ${\beta }_1=\cdots ={\beta }_k=\sqrt{2\text{log}p}\approx 3.65,\sigma =1$.

Tables 1 and 2 in Service et al. (2014) describe a total of 14 variants as having an effect on HDL: two of these are for regions FADS1 and MVK and the strength of the evidence in this specific data set is quite weak (a marginal p-value of the order of 10⁻³). Multiple effects are identified in regions ABCA1, CEPT, LPL and LIPL. The results of the various “model selection” strategies we explored are in Figure 11, which reports the estimated values of the coefficients. The effect of the shrinkage induced by Lasso and SLOPE are evident. To properly compare effect sizes across methods, it would be useful to resort to the two-step procedure that we used for the simulation described in Figure 2. Since our interest here is purely model selection, we report the coefficients directly as estimated by the ℓ₁ penalized procedures; this has the welcome side effect of increasing the spread of points in Figure 11, improving visibility.

FIG. 11.

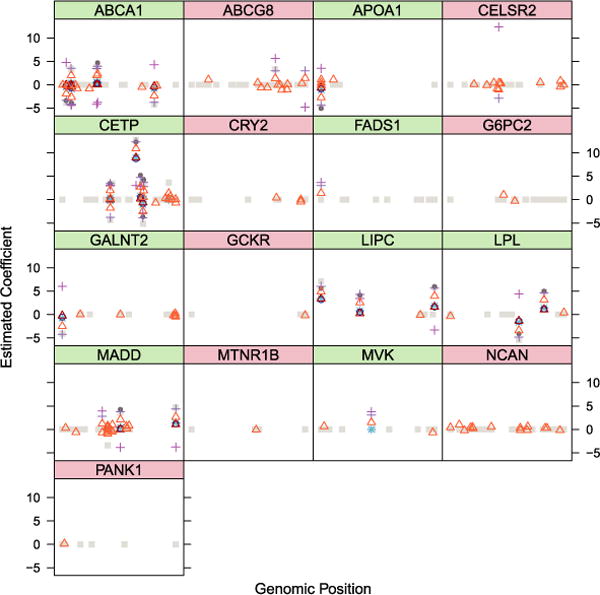
Estimated effects on HDL for variants in 17 regions. Each panel corresponds to a region and is identified by the name of a gene in the region, following the convention in Service et al. (2014). Regions with (without) previously reported association to HDL are on the green (red) background. On the x-axis variants position in base-pairs along their respective chromosomes. On the y-axis estimated effect according to different methodologies. With the exception of marginal tests—which we use to convey information on the number of variables and indicated with light gray squares—we report only the value of nonzero coefficients. The rest of the plotting symbols and color convention is as follows: dark gray bullet—BH on p-values from full model; magenta cross—forward BIC; purple cross—backward BIC; red triangle—Lasso–λ_Bonf; orange triangle—Lasso–λ_CV; cyan star—SLOPE– ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$; black circle—SLOPE with λ defined with Monte Carlo strategy.

Of the 14 variants described in Service et al. (2014), 8 are selected by all methods. The remaining 6 are all selected by at least some of the 8 methods we compared. There are an additional 5 variants that are selected by all methods but are not in the main list of findings in the original paper: four of these are rare variants, and one is an array SNP for a trait other than HDL. While none of these, therefore, was singularly analyzed for association in Service et al. (2014), they are in highlighted regions: one is in MADD, and the others in ABCA1 and CETP, where the paper documents a plurality of signals.

Besides this core of common selections that correspond well to the original findings, there are notable differences among the 8 approaches we considered. The total number of selected variables ranges from 15, with BH on the p-values of the full model, to 119, with the cross-validated Lasso. It is not surprising that these methods would result in the extreme solutions. On the one hand, the p-values from the full model reflect the contribution of one variable given all the others, which are, however, not necessarily included in the models selected by other approaches; on the other hand, we have seen how the cross-validated Lasso tends to select a much larger number of variables and offers no control of FDR. In our case, the cross-validated Lasso estimates nonzero coefficients for 90 variables that are not selected by any other methods. Note that the number of variables selected by the cross-validated Lasso changes in different runs of the procedure, as implemented in glmnet with default parameters. It is quite reasonable to assume that a large number of these are false positives: regions G6PC2, PANK1, CRY2 and MTNR1B, where the Lasso–λ_CV selects some variants, have no documented association with lipid levels, and regions CELSR2, GCKR, ABCG8 and NCAN have been associated previously to total cholesterol and LDL, but not HDL. The other procedures that select some variants in any of these regions are the forward and backward greedy searches trying to optimize BIC, which have hits in CELSR2 and ABCG8, and the BH on univariate p-value, which has one hit in ABCG8. SLOPE does not select any variant in regions not known to be associated with HDL. This is true also of the Lasso–λ_Bonf and BH on the p-values from the full model, but these miss, respectively, 2 and 6 of the variants described in the original paper, while SLOPE ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ misses only one of them.

Figure 12 focuses on the set of variants where there is some disagreement between the 8 procedures we considered, after eliminating the 90 variants selected only by the Lasso–λ_CV. In addition to recovering all except one of the variants identified in Service et al. (2014), and to the core of variants selected by all methods, SLOPE– ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ selects 3 rare variants and 3 common variants. While the rare variants were not singularly analyzed in the original study, they are in the two regions where aggregate tests highlighted the role of this type of variation. One is in ABCA1 and the other two are in CETP, and they are both nonsynonimous. Two of the three additional common variants are in CETP and one is in MADD; in addition to SLOPE, these are selected by Lasso–λ_CV and the marginal tests. One of the common variants and one rare variant in CETP are mentioned as a result of the limited foray in model selection in Service et al. (2014). SLOPE–λ_MC selects two less of these variants.

FIG. 12.

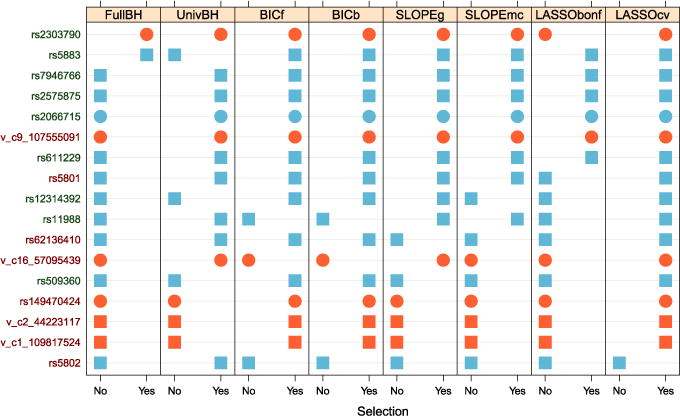
Each row corresponds to a variant in the set differently selected by the compared procedures, indicated by columns. Orange is used to represent rare variants and blue common ones. Squares indicate synonymous (or noncoding variants) and circles nonsynonimous ones. Variants are ordered according to the frequency with which they are selected. Variants with names in green are mentioned in Service et al. (2014) as to have an effect on LDL, while variants with names in red are not [if a variant was not in dbSNP build 137, we named it by indicating chromosome and position, following the convention in Service et al. (2014)].

In order to get a handle on the effective FDR control of SLOPE in this setting, we resorted to simulations. We consider a number k of relevant variants ranging from 0 to 100, while concentrating on lower values. At each level, k columns of the design matrix were selected at random and assigned an effect of $\sqrt{2\text{log}p}$ against a noise level σ set to 1. While analyzing the data with λ_MC and ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$, we estimated σ from the full model in each run. Figure 10(b)–(c) reports the average FDP across 500 replicates and their standard error: the FDR of both λ_MC and ${\mathrm{\lambda }}_{{\mathrm{G}}^{\star }}$ are close to the nominal levels for all k ≤ 100.

In conclusion, the analysis with SLOPE confirms the results in Service et al. (2014), does not appear to introduce a large number of false positives and, hence, makes it easier to include in the final list of relevant variants a number of polymorphisms that are either directly highlighted in the original paper or in regions that were described as including a plurality of signals, but for which the original multi-step analysis did not allow to make a precise statement.

4. Discussion

The ease with which data are presently acquired has effectively created a new scientific paradigm. In addition to carefully designing experiments to test specific hypotheses, researchers often collect data first, leaving question formulation to a later stage. In this context, linear regression has increasingly been used to identify connections between one response and a large number p of possible explanatory variables. When $p\gg n$, approaches based on convex optimization have been particularly effective. An easily computable solution has the advantage of definitiveness and of reproducibility—another researcher, working on the same data set, would obtain the same answer. Reproducibility of a scientific finding or of the association between the outcome and the set of explanatory variables selected among many, however, is harder to achieve. Traditional tools such as p-values are often unhelpful in this context because of the difficulties of accounting for the effect of selection. In response, a great number of proposals [see, e.g., Benjamini and Yekutieli (2005), Berk et al. (2013), Bühlmann (2013), Efron (2011), Javanmard and Montanari (2014a, 2014b), Lockhart et al. (2014), Meinshausen and Bühlmann (2010), Meinshausen, Meier and Bühlmann (2009), van de Geer et al. (2014), Wasserman and Roeder (2009), Zhang and Zhang (2014)] present different approaches for controlling some measures of type I error in the context of variable selection. We here chose as a useful paradigm that of controlling the expected proportion of irrelevant variables among the selected ones. A similar goal of FDR control is pursued in Foygel-Barber and Candès (2014), Grazier G’Sell, Hastie and Tibshirani (2013). While Foygel-Barber and Candès (2014) achieve exact FDR control in finite sample irrespective of the structure of the design matrix, this method, at least in the current implementation, is really best tailored for cases where n > p. The work in Grazier G’Sell, Hastie and Tibshirani (2013) relies on p-values evaluated as in Lockhart et al. (2014), and is limited to the contexts where the assumptions in Lockhart et al. (2014) are met, including the assumption that all true regressors appear before the false regressors along the Lasso path. SLOPE controls FDR under orthogonal designs, and simulation studies also show that SLOPE can keep the FDR close to the nominal level when p > n and the true model is sparse, while offering large power and accurate prediction. This is, of course, only a starting point and many open problems remain.

First, while our heuristics for the choice of the λ sequence allows to keep FDR under control for Gaussian designs and other random design matrices [more examples are provided in Bogdan et al. (2013)], it is by no means a definite solution. Further theoretical research is needed to identify the sequences λ, which would provably control FDR for these designs and other typical design matrices.

Second, just as in the BH procedure where the test statistics are compared with fixed critical values, we have only considered in this paper fixed values of the regularizing sequence {λ_i}. It would be interesting to know whether it is possible to select such parameters in a data-driven fashion as to achieve desirable statistical properties. For the simpler Lasso problem, for instance, an important question is whether it is possible to select λ on the Lasso path as to control the FDR. In the case where n ≥ p, a method to obtain this goal was recently proposed in Foygel-Barber and Candès (2014). It would be of great interest to know if similar positive theoretical results can be obtained for SLOPE, in perhaps restricted sparse settings.

Third, our research points out the limits of signal sparsity which can be handled by SLOPE. Such limitations are inherent to ℓ₁ convex optimization methods and also pertain to Lasso. Some discussion on the minimal FDR which can be obtained with Lasso under Gaussian designs is provided in Bogdan et al. (2013), while new evocative results on adaptive versions of Lasso are on the way.

Fourth, we illustrated the potential of SLOPE for multiple testing with positively correlated test statistics. In our simple ANOVA model, SLOPE controls FDR even when the unknown variance components are replaced with their estimates. It remains an open problem to theoretically describe a possibly larger class of unknown covariance matrices for which SLOPE can be used effectively.

In conclusion, we hope that the work presented so far would convince the reader that SLOPE is an interesting convex program with promising applications in statistics and motivates further research.