A Comparative Analysis of Speed Profile Models for Wrist Pointing Movements

Abstract

Following two decades of design and clinical research on robot-mediated therapy for the shoulder and elbow, therapeutic robotic devices for other joints are being proposed: several research groups including ours have designed robots for the wrist, either to be used as stand-alone devices or in conjunction with shoulder and elbow devices. However, in contrast with robots for the shoulder and elbow which were able to take advantage of descriptive kinematic models developed in neuroscience for the past 30 years, design of wrist robots controllers cannot rely on similar prior art: wrist movement kinematics has been largely unexplored. This study aimed at examining speed profiles of fast, visually evoked, visually guided, target-directed human wrist pointing movements. One thousand three-hundred ninety-eight (1398) trials were recorded from seven unimpaired subjects who performed center-out flexion/extension and abduction/adduction wrist movements and fitted with 19 models previously proposed for describing reaching speed profiles. A nonlinear, least squares optimization procedure extracted parameters’ sets that minimized error between experimental and reconstructed data. Models’ performances were compared based on their ability to reconstruct experimental data. Results suggest that the support-bounded log-normal is the best model for speed profiles of fast, wrist pointing movements. Applications include design of control algorithms for therapeutic wrist robots and quantitative metrics of motor recovery.

I. Introduction

Stroke is a leading cause of permanent disability worldwide. Every year over 785 000 persons suffer a stroke in the U.S. and about 70% of stroke survivors lose motor skills of the arm and hand [1]. First proposed in the late 1980s, robot-mediated therapy is increasingly becoming part of post-stroke rehabilitative care. Several rehabilitation robots for the upper extremity have been proposed, including MIT-Manus [2], ARM Guide [3], MIME [4], and the more recently developed PLEMO [5], ARMin [6], and MEMOS [7]. Clinical effectiveness greater than sham robot-therapy or a matched amount of traditional therapy has been reported by several studies [4], [8]–[10], including the recent Veterans Administration multicenter, randomized, controlled clinical trials reported in the New England Journal of Medicine [11]. While these devices mainly target motor therapy at the shoulder and elbow joints, it has long been known that improvements observed at these joints do not generalize to wrist and hand [12]. To overcome this limitation, several wrist devices have been proposed in the last few years, including the MIT wrist robot [13], RiceWrist [14], HWARD [15], the Okayama University pneumatic manipulator [16], and the IIT wrist robot [17]. These robots can be used either as standalone therapy devices for wrist rehabilitation or coupled with other devices such as MIT-MANUS [18], ARMIN [19], HapticMaster [20], and wire-based device from [21] to deliver robot therapy to the whole upper limb.

Despite the recent proliferation of hardware for delivering therapy to the upper limb and clinical studies reporting on the efficacy of robot-mediated therapies, how to design control strategies able to maximize patients’ motor recovery remains a major issue for the field regardless of the joint targeted by the therapy. This is arguably due to two factors, i.e., poor understanding of mechanisms underlying stroke recovery and of neural control of movement [22]. Compared to the design of controllers for therapeutic robots for the shoulder and elbow, the design of controllers for wrist therapeutic robots presents an additional major challenge: it can draw from results of prior neuroscience studies in only a very limited fashion.

Upper limb movements involving shoulder and elbow joints have been intensively studied since the 1980s in the motor control and neuroscience community. Early studies aimed at characterizing and modeling kinematics of reaching movements [23]. Rapid target-directed reaching movements were found to be virtually straight with a bell-shaped, nearly symmetric speed profile [24]–[27]. More complex movements, such as drawing and handwriting, displayed less smooth speed profiles, which were modeled as a combination of elementary movements (submovements) whose shape was identified via optimization techniques [28]–[30]. Such results prompted a number of subsequent investigations, which led to models of how the Central Nervous System (CNS) controls and learns reaching movements (for example, [31]–[33]). These data have found numerous applications in rehabilitation robotics, from design of controllers for shoulder and elbow therapeutics robots [34], [35] to design of quantitative metrics for patients’ motor recovery and performance [36]–[38].

Compared to arm movements, our current understanding of wrist motion is, however, remarkably poor. So far, only a few studies have focused on the wrist joint. Most reported on measured data for surgical applications, such as individual carpal bone motions and wrist range of motion [39]–[41]. It was just recently that Charles et al. [42], [43] showed that, similar to primates [44], wrist movement trajectories in humans are more variable and curved than reaching trajectories, exhibiting roughly twice as much curvature. Using mechanical perturbations, our group also characterized motor adaptation in the wrist and found that adaptation in the wrist is more difficult to detect than motor adaptation in reaching, presumably due to the higher variability of wrist trajectories compared to reaching [45].

Recently, we started designing performance-based adaptive controllers for our wrist rehabilitation robots [13]. The lack of descriptive models able to characterize wrist kinematics makes such performance-based designs challenging. The goal of this study was to select a competent model for wrist movement speed profiles. Can we analyze such profiles using the same “machinery” that was developed over the past decades for arm movements? Specifically, can we model wrist movements’ speed profiles using the models developed for arm reaching speed profiles? While arm movements may be defined as points in a vector space, wrist movements are defined by finite spatial rotations, which do not form a vector space [46]. Such a fundamental difference may entail different computational challenges for the CNS and ultimately result in different control strategies and kinematic features of movement [45].

In this study, we investigated kinematic models previously proposed to describe reaching and handwriting movements. Specifically, we selected the models from the comparative studies by Plamondon et al. [30] and Stein et al. [47]. We recorded and analyzed the speed profiles of 1398 fast, target-directed wrist movements; for each movement and model, we used a nonlinear, least squares optimization procedure to extract a set of parameters that minimized the error between the experimental data and the reconstructed speed profiles. We then compared the models’ performances in terms of reconstruction errors using a reconstruction error threshold from a comparable study for reaching movements by Flash and Hogan [26]. Our goal was to determine whether any of the previously proposed models for reaching satisfied this bound, or, alternatively, whether new models should be investigated.

II. Methods

A. Apparatus

This study used an InMotion3 wrist robot (Interactive Motion Technologies, Watertown, MA). The robot had three actuated degrees-of-freedom (DOF), i.e., wrist abduction/adduction and flexion-extension, and forearm pronation-supination. A complete description of the hardware is reported elsewhere but suffice to say that the robot hardware is highly “backdrivable,” i.e., it easily gets “out of the way” of the subject [13]. The angular positions of encoders located at the joints of the robot were acquired digitally (sampling frequency fs = 1kHz, 16-bit quantization).

B. Subjects

Seven young, healthy subjects (age range 18–35 years) participated in this study. Subjects had no history of neurological disorders. Experiments were approved by MIT’s Committee on the Use of Humans as Experimental Subjects, and informed consent was obtained from all subjects.

C. Experimental Procedure

Subjects were seated in front of a computer monitor and held the handle of the robot in their dominant right hand. Their upper arm was restrained by a Velcro-strapped belt and their forearm was supported in the horizontal plane and restrained with a Velcro-strapped belt (Fig. 1). To have them replicate pointing movements during therapy, the robot pronation/supination DOF was locked, restricting movement only to flexion/extension and abduction/adduction plane.

Fig. 1.

InMotion3 wrist robot.

Two experiments were performed. In the first experiment, two outer targets on a circle at East and West position and a central target (neutral wrist position) were displayed. Subjects were instructed to move the handle of the robot corresponding to a screen cursor between the central target and the outer targets (target diameter = 2.5 cm). Outer targets were presented in a random order, but each was presented an equal number of times. The central target was presented following each of the outer targets. Targets remained lit for 0.8 s. For the first 0.4 s of this period, the target was one color and then it turned into a different color. Subjects were instructed to reach the target about the time when its color changed. After the 0.8 s a new target lit up. Subjects were given no explicit instruction regarding the trajectory and performed 160 movements per direction (80 movements from the central to the outer targets and 80 movements back). The second experiment was similar to the first experiment, but the outer targets were displayed at the North and South positions. The motor tasks required by the first and second experiment were flexion/extension and abduction/adduction of the wrist, which required 30 and 15 degrees, respectively. These movement ranges were selected to allow for comfortable movements covering approximately 50% of the ranges of motion of a normal wrist (flexion/extension 60/60 degrees, abduction/adduction 30/45 degrees, pronation/supination 70/70 degrees, see [13]). Prior to starting any recording, subjects practiced the motor tasks as needed until they were fully comfortable performing them.

D. Speed Profiles Computation and Modeling

Speed profiles for all movements were computed as

$$v=\sqrt{{\left(\frac{dr}{dt}\right)}^2+r^2{\text{sin}}^2(\phi ){\left(\frac{d\theta }{dt}\right)}^2+r^2{\left(\frac{d\phi }{dt}\right)}^2}$$

where θ and ϕ were the azimuth and zenith coordinates recorded by the robot [48]. The radial coordinate was assumed to be constant and equal to 9 cm. The derivatives were computed numerically using Savitzky-Golay filters with fourth order polynomial fit and window width of 17 samples. Data segments for modeling were extracted as following. The time point t_max was found, at which the maximum value of the speed profile occurred. By moving to the left and to the right from t_max by one time point increments, times t_lb and t_ub closest to t_max were found such that t_lb < t_max < t_ub, with v(t_lb) < 0.05*v(t_max) and v(t_ub) < 0.05*v(t_max). The speed profile segments between t_lb and t_ub were extracted and their plots were visually inspected to verify that they contained only a single large peak. Data segments containing other large peaks, defined as larger than 20% of the higher peak due to corrective movements, were discarded. The purpose of such a selection was to ensure that modeled speed profiles corresponded to single movements in each direction. On average, 28 and 22 out of 40 speed profiles per movement direction were selected for center-out and back movements respectively (for a total of 1398 profiles).

Because the extracted speed profiles segments had different length (time duration), we normalized movement duration to a range using the procedure described in [26]. We subtracted from all time points values for a given speed profile and then divided resultant time points by t_ub−t_lb value. The data was not re-sampled, and each speed profile retained its original number of points.

For every speed profile, duration of movement, peak and average speed, skewness, kurtosis and “symmetry ratio” were computed. Because skewness and kurtosis are defined only for probability distributions [49], the area under the speed profile curve was normalized to 1. This was done after the time points range was converted to be from 0 to 1 (although the time points range conversion does not affect this calculation). Skewness and kurtosis were then evaluated by standard formulae using the normalized speed profile as a probability distribution function. Skewness = E[(x − x̄)³]/σ³, Kurtosis = E[(x − x̄)⁴]/σ⁴, where x are the normalized speed profile values, x̄ is a mean and σ is the standard deviation of the normalized speed profile. Symmetry ratio was introduced to serve as an additional estimate of data’s asymmetry, in addition to skewness, and was defined as (t_max−t_lb)/(t_ub−t_max). When the ratio is equal to 1, the peak is exactly in the middle of the data.

The equations of the models used in this study are listed in the Appendix. The interior-reflective Newton algorithm, which was implemented in MATLAB function lsqcurvefit (Mathworks Inc., Natick, MA), was used to solve a nonlinear, least squares problem of optimal selection of parameters in models’ equations [50]. Initialization values (also listed in Appendix) were selected by trial and error in order to achieve convergence for each model to the recorded speed profile. The optimization algorithm was allowed to run for at least 100 000 iterations or until the change in squared sum of the residuals became less than 10⁻⁹.

To compare different models, the Akaike Information Criterion (AIC) was used as performance index. This was given by: AIC = N * ln(SSE/N)+2 * K+2 * K * (K+1)/(N−K−1), where SSE is the sum of squared errors (residuals) returned by the optimization algorithm, is equal to the number of points in the fit, and is equal to the number of model parameters plus one [51]. Lower AIC indicates a better fit. We constructed two bar plots to afford visualization of the results: 1) for each speed profile, a model was awarded one point if its AIC was among the five best performers for that profile (lower AIC). This will be referred to as the “Top 5” plot; and 2) for each speed profile, we ranked the models with best performer awarded 18 points, 17 if its AIC was second lowest, etc. We normalized the resulting summation of all profiles by dividing the cumulative sum for each model by the number of profiles that contributed to the sum. This will be referred to as “Score 18” plot. “Top 5” and “Score 18” plots were constructed for each subject and for each movement direction separately. Because the results for sets of speed profiles recorded from different subjects and different directions were consistent (i.e., the groups of best fitting and worst fitting models were essentially the same for all the sets, while other models’ performance did not strongly fluctuate among the sets), we grouped all speed profiles together for statistical analysis. Fitting accuracy of models was computed as the percent error between the area under the modeled speed profile and that under the recorded speed profile.

E. Statistical Analysis

A Kruskal-Wallis 1-way ANOVA followed by multiple comparisons test was performed on AIC values for all modeled speed profiles [49]. Nonparametric statistics were used because series of AIC values for many models did not have a Gaussian distribution. Tests were performed with 5% significance level.

III. Results

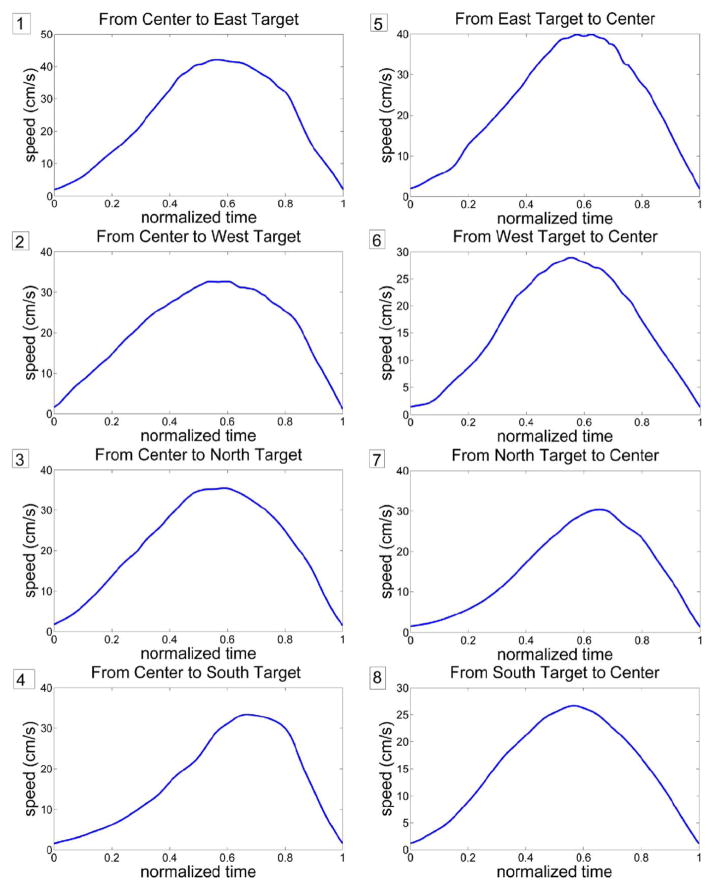
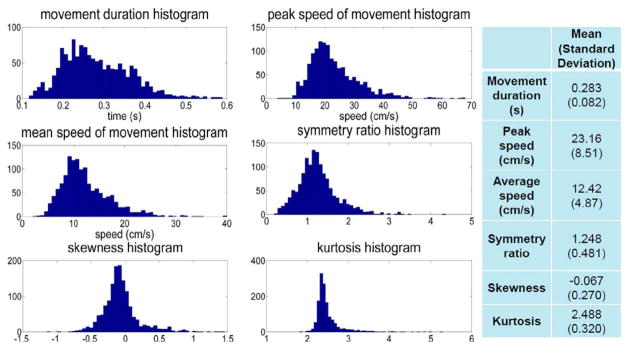
Fig. 2 shows a typical set of speed profiles for center-out and back movements. Fig. 3 shows histograms, mean and standard deviation values of the parameters extracted from the speed profiles. Most movements were about 0.2–0.4 s long, with most peak speeds between 10 and 50 cm/s, and average speeds between 5 and 30 cm/s. Skewness and symmetry ratio histograms show that a larger portion of the data had slightly negative skewness, i.e., longer tail to the left, or the peak speed value closer to the end rather than the beginning of movement. Kurtosis values mainly ranged between 2 and 3.

Fig. 2.

Sample set of speed profiles for all directions of movement. Legend: 1: Center to East target, 2: Center to West target, 3: Center to North target, 4: Center to South target, 5: East target to Center, 6: West target to Center, 7: North target to Center, 8: South target to Center. All horizontal axis are normalized time and all vertical axis are speed in centimeters per second.

Fig. 3.

Histograms of parameters extracted from speed profiles and their mean and standard deviation values.

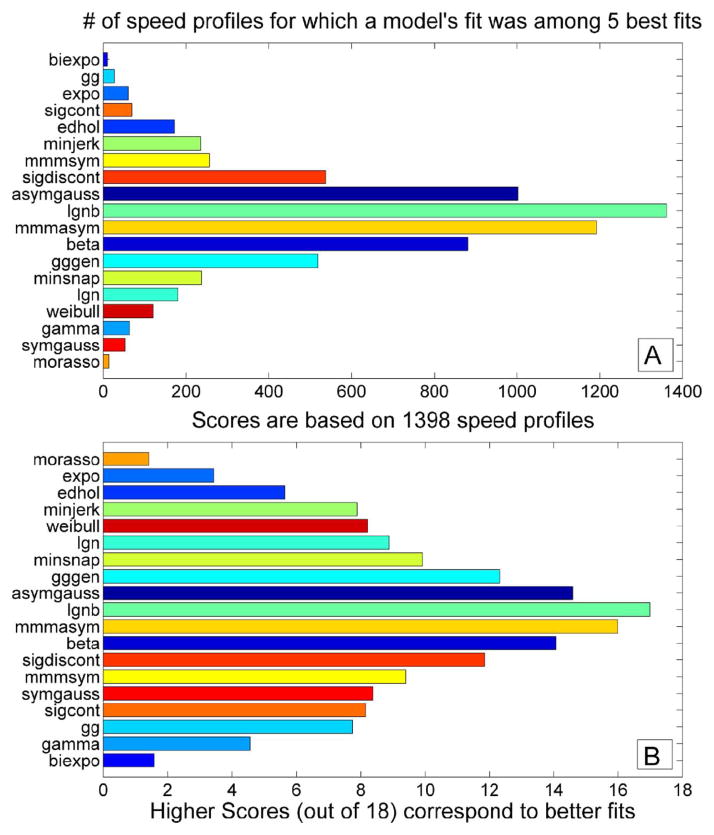
Fig. 4(a) shows the cumulative “Top 5” plot. Four models stand out as the top five best fits, i.e., their AIC values were most commonly among the five lowest. These are lognormal with support bound (LGNB), Morasso Mussa-Ivaldi and Maarse asymmetric (MMMasym), asymmetric Gaussian and beta function models. Overall, symmetric models performed worse than asymmetric ones with the best of symmetric models, namely Morasso, Mussa-Ivaldi and Maarse symmetric model (MMMsym) scoring seventh. Fig. 4(b) shows the cumulative “Score 18” plot. This scoring system favors consistent high level of performance. It allows a somewhat more balanced comparison between the models. The four best models are the same as in the “Top 5” plot. However, some models—in particular minimum snap, lognormal without support bound (LGN) and generalized Gutman & Gottlieb model (GGgen)—have improved their relative placement because they were consistently performing even though they were not that often among the five best fits for speed profiles. On the other hand, models like MMMsym and minimum jerk have been ranked higher on “Top 5” plot than “Score 18” plots because, although they performed very well for some profiles ranking on the “Top 5” plot, they did not have very consistent performance for a large number of profiles, and thus were ranked lower overall. The models that did not perform well under-performed in both “Top 5” and “Score 18” plots. These included Plamondon-Lamarche exponential, Eden and Hollerbach, minimum acceleration (Morasso), gamma function, and biexponential models.

Fig. 4.

A) Cumulative “top 5” plot based on 1398 speed profiles. Four models—LGNB, MMMasym, asymmetric Gaussian and beta function—were most consistently among top 5 best fits based on AIC for speed profiles. B) Cumulative “score 18” plot based on 1398 speed profiles. The same four models as on the “top 5” plot were the top performers.

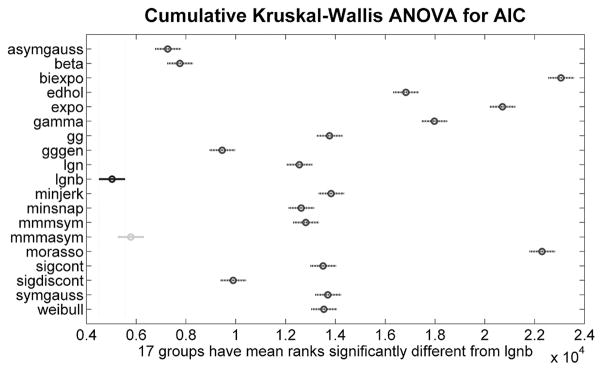
Results of statistical analysis are shown in Fig. 5. The models closer to the left side of the plot have lower median ranks and therefore performed better. On the whole, the results shown in Fig. 5 are consistent with those shown in the “Score 18” plot: LGNB, MMMasym, asymmetric Gaussian, beta function, GGgen and sigmoidal discontinuous models have the lowest median AICs. Eight models follow with approximately the same level of median ranks, while the remaining five models performed quite poorly.

Fig. 5.

Results of Kruskal-Wallis ANOVA and multiple comparisons’ test on AIC for different models for 1398 speed profiles. LGNB model’s median ranks are in black as the top performer, other models’ median ranks are in dark-gray if statistically significantly different from it to 5% significance level and in light-gray if not. Overall, the results of this plot are consistent with the ranking of models in “score 18” plot.

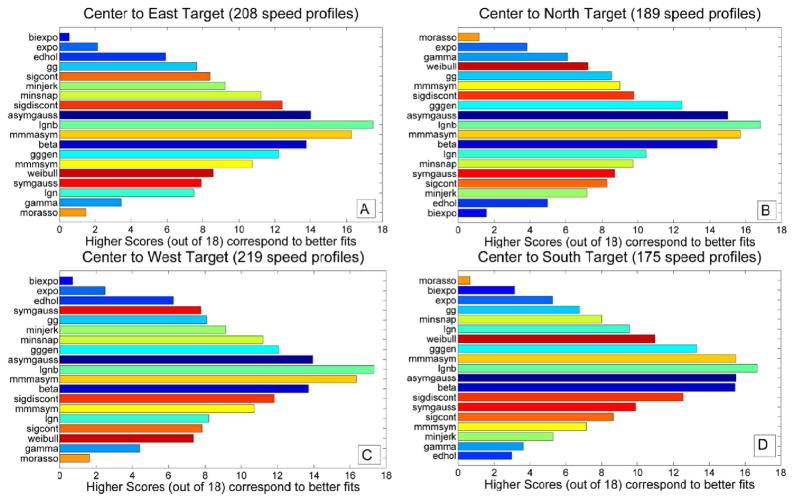
Analysis of the goodness of a particular model’s fit for each individual direction showed that results were essentially independent of the movement direction. Fig. 6 shows “Score 18” plots for different directions. Plots are generally very similar to the “Score 18” plot for all modeled profiles combined shown in Fig. 4(b), namely the top/worst performing models shown in Fig. 4(b) were the top/worst performing models for the different directions.

Fig. 6.

“Score 18” plots computed based on movements in specific directions from center to targets. MMMasym, asymmetric Gaussian, beta function, and LGNB model are consistently among the top performers. Panels A, B, C, and D show performance of models for movements in East, North, West, and South direction, respectively.

Table I shows the percent of errors of areas under the modeled and recorded speed profiles. For six models, including LGNB, MMMasym, asymmetric Gaussian, beta function, GGgen, and sigmoidal discontinuous, the error was below 4% for over 50% of speed profiles.

TABLE I.

Percent Errors Between Areas Under Modeled and Recorded Speed Profiles for Different Models

Model	Mean % error	Standard Deviation of % error	% of Speed Profiles with Error <=4%
LGNB	3.26	2.99	77.25
MMMasym	3.37	2.66	74.89
Asymgauss	3.72	2.7	74.17
Beta	4.25	3.38	66.95
GGgen	4.97	4.3	57.87
LGN	6.11	3.34	25.18
Sigdiscont	6.16	8.92	58.01
Symgauss	7.06	5.68	20.46
Weibull	7.19	5.38	23.75
GG	7.24	4.85	25.18
Minsnap	7.34	5.97	34.55
MMMsym	7.35	5.86	32.83
Sigcont	7.59	7.07	13.73
Minjerk	8.24	6.58	26.39
Gamma	9.86	4.4	4.22
Edhol	10.43	7.55	16.17
Expo	11.07	2.83	0.07
Biexpo	15.3	2.13	0
Morasso	16.91	9.21	0.57

IV. Discussion

A. Features of Wrist Movements Speed Profiles

In this study we recorded and analyzed speed profiles of fast, visually evoked, visually targeted wrist pointing movements involving wrist flexion/extension and abduction/adduction. Our robot-mediated therapy protocols trains pointing movements in the spherical surface determined by these wrist motions and train separately pronation/supination movements. As in our robot-mediated therapy and similar to previous psychophysical studies [42], [52]–[59], we locked the pronation/supination DOF. Under this setup, the robotic device had near isotropic inertia properties in flexion/extension and abduction/adduction movements with minimal interference in trajectory formation. Note that wrist trajectories recorded with the robot were found indistinguishable from those recorded without the robot (i.e., with Flock of Birds, Ascension Technologies, VT) for movements of the wrist encompassing flexion/extension and abduction/adduction [42] (but not for movements involving pronation/supination [60]).

The wrist movement peak speeds obtained in our experiment (10–50 cm/s, or 60–320 degrees/s) were comparable to the peak wrist movement speed values reported by Yayama et al. [61], who measured wrist flexion/extension and abduction/adduction movements in five young healthy subjects. This comparison is meaningful because the flexion/extension and abduction/adduction cycles in the study of Yayama et al. were performed at a rate of one cycle per second, and our extracted portions of speed profiles had movement duration of 0.1–0.6 s (Fig. 3, top left panel), i.e., movement durations were similar. Our peak values were overall greater than those reported by Rosen et al. [62], who measured ranges of motion and speed of wrist movements during daily tasks. For example, Rosen et al. reported that during the task of eating with a spoon, maximum velocities were 34 degrees/s in the direction of flexion, 24.5 degrees/s in the direction of extension, 25.1 degrees/s for radial deviation, and 44.7 degrees/s for ulnar deviation.

Skewness and symmetry ratios analyses yielded similar results (Fig. 3). They showed that the larger proportion of data was asymmetric; consistently, asymmetric models of speed profiles performed better than symmetric ones. Kurtosis values overall were less than those expected for symmetric Gaussian curves (3), i.e., speed profiles mostly appeared to be platykurtic, with smaller tails and wider peaks.

B. Models Selection

This study compared the ability of 19 models to describe accurately the speed profiles of fast, visually evoked, visually targeted wrist pointing movements. The characterization of the best speed profile constitutes a necessary step for developing theories of motor control and learning [26], [31]–[33], controllers for therapeutic robots for stroke rehabilitation [35], and quantitative metrics of motor recovery from stroke [37], [38], [63] for arm movements.

We selected from the literature speed profiles models for human upper limb movements with different complexity, including reaching, drawing, and handwriting. In particular, we selected the models from the comparative studies by Plamondon et al. [30] and Stein et al. [47]. From their lists we excluded the models that had many more parameters than others and were found to have very low performance.

The selected models differ for several technical features, including number of parameters and differentiability properties. Historically, starting from the 1970s, such models were developed by investigators interested in different components of the motor system and reflected different views on upper limb motor control and mechanisms of trajectory formation. Kinematics-oriented models assume that such mechanisms are independent of the actual joint and muscle patterns and depend only on the CNS capability to control the trajectory of the hand in space. Conversely, dynamics-based models assume that trajectory formation mechanisms are directly related to the geometry and mechanical properties of muscles, which can be seen as generators of force, oscillation, or speed [30]. Kinematic-oriented models include the Morasso model [29] and its modified versions [64], minimum jerk [26], minimum snap [65], Gutman and Gottlieb (GG) [66], Gaussian, LGN and LGNB [67]–[69], and beta, gamma, and Weibull models [30], [69]. In the Morasso model [29], movement is described as a sequence of basic strokes of given length, tilt angle and angular change; each basic stroke is described as a symmetric continuous bell-shape (cubic spline function). The Morasso, Mussa-Ivaldi and Maarse models [64] represent bell-shaped profiles with cosine functions instead of splines. The minimum jerk [26] and minimum snap [65] models consider trajectories of movement to be obtained by minimizing the jerk and the snap, i.e., the third- and fourth-time derivative of displacement which can be described by fifth- and seventh- order polynomials respectively. The GG model [66] describes trajectories with an exponential function, whose specific shape depends on two parameters, distance and a movement time constant. Plamondon and colleagues’ models mostly aimed at investigating the role of shape symmetry. They include: Gaussian models, which use Gaussian functions and can produce symmetric continuous as well as asymmetric discontinuous profiles [30], [70]; LGN and LGNB models, which are derived as converging behavior of a system of a sequentially acting cascade of velocity generators [30], [67], [69], [71] and can produce asymmetric and continuous profiles; GGgen model (asymmetric continuous); sigmoidal models (asymmetric continuous and discontinuous); gamma model (asymmetric continuous); beta model (asymmetric continuous); and Weibull model (asymmetric continuous). Note that the discontinuous models were originally proposed for handwriting, and handwriting velocity consists of curvilinear and angular components, where angular component can be discontinuous [70].

Dynamic-oriented models include Eden-Hollerbach [72], and Plamondon and Lamarche [73] models. The Eden-Hollerbach model [72] considers muscles as harmonic oscillators and handwriting as generated by orthogonal oscillations horizontal and vertical in the plane of the writing surface. This model produces symmetric continuous profiles. Plamondon and Lamarche [73] model assumes that the whole nerve muscle system behaves as speed generators, which can be described with transfer functions that generate bell-shaped curvilinear speed profiles given a rectangular pulse as input and can work in parallel. This model yields to asymmetric discontinuous profiles. Our list of models also included the biexponential model, which was proposed by Stein et al. [47] to describe wrist movements along with the symmetric Gaussian, minimum jerk, and Morasso model. To the best of our knowledge, the mechanisms underlying wrist motor control and trajectory formation have not been investigated. However, similar to Plamondon et al. [30], we analyzed these models with the point of interest fixed on their performance in reproducing speed profiles of simple, fast target-directed wrist movements. This focus is consistent with our goal, which is to identify suitable mathematical descriptions of wrist speed profiles to be used in the design of robotic tools for neurorehabilitation and of quantitative metrics of motor recovery after brain injury.

C. Comparison With Reaching

Our result that asymmetric models performed better than symmetric models is consistent with the findings of the work of Plamondon et al. [30] that investigated drawing movements. Plamondon and colleagues also found that the LGNB model strongly outperformed the other models. Asymmetric Gaussian and discontinuous sigmoidal models were in the top six performing models both for Plamondon’s data as well as for our wrist data (Figs. 4 and 5). Poorly performing models in our data (Eden-Hollerbach, gamma function, Morasso, biexponential and Plamondon-Lamarche exponential models) were also among the poorly performing models in Plamondon et al. However, MMMasym and MMMsym models, which in our data were in top two best asymmetric and symmetric models respectively, did not perform well in Plamondon’s data. Such a discrepancy might be explained by differences in the nature of performed tasks. Morasso, Mussa Ivaldi and Maarse models were originally proposed for modeling handwriting, which mainly consists of curved elements: they assumed that the segment between the points of minimum speed was an arc of a circle [29]. The wrist movements we recorded, which required wrist flexion/extension and abduction/adduction, may have been closer to the arc of the circle shape [42] than the pen-tip fast straight strokes of Plamondon et al. That wrist movement trajectories are not straight but are curved, with a curvature higher than that displayed by reaching trajectories, was shown by Charles and Hogan [74]. To verify the presence of nonzero curvature in the recorded wrist movement trajectories, we estimated the curvature as the area bounded by the path and a straight line connecting the start and end points of the path [43]. Thirty-two out of 56 groups of trajectories (seven subjects, four directions from center to target and four directions back) displayed median trajectory curvature significantly different statistically from 0 (corresponding to the curvature of a straight line). The Wilcoxon signed-rank test at 5% significance level was used for hypothesis testing [49].

The observation that asymmetric models perform better than the symmetric ones is also consistent with prior work that showed that single-joint movements often have asymmetric speed profiles [75]–[78]. A plausible neurophysiological argument for explaining asymmetry was proposed by Jaric et al. [79], who suggested that asymmetry may be caused by either muscle viscosity or patterns of muscle activation. Further work, including a characterization of asymmetry as a function of movement velocity, is required to identify possible sources of asymmetry in wrist movements’ speed profiles. Our results are consistent with the work of Stein et al. [47], who investigated four models for speed profiles of wrist movements, i.e., minimum jerk, Morasso, biexponential and symmetric Gaussian models. They found that symmetric, Gaussian fitted wrist movement speed profiles performed better than minimum jerk, which in turn performed better than two other models. This result is consistent with the results shown in the “Score 18” and Kruskal-Wallis plots (Figs. 4 and 5).

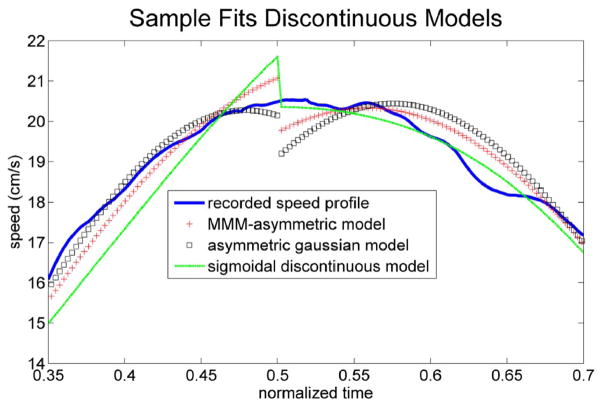
Of notice, several models were able to fit most speed profiles with an error below 4%. This error threshold is the same used in the seminal paper by Flash and Hogan [26] to assess the performance of their model in fitting speed profiles of reaching movements. These models included LGNB, MMMasym, asymmetric Gaussian, beta function, GGgen and sigmoidal discontinuous models. Not surprisingly, these models were also the top performers when goodness of fit was assessed by means of the AIC criterion on “Top 5” and “Score 18” histograms. Of course, we cannot accept or reject models purely on the ground of the mathematical goodness of their fits. Several important physical factors are also to be considered. One such factor is continuity of the speed profiles. This is important because a discontinuous model of the speed profile results in infinite acceleration at the point of discontinuity, which is not achievable in wrist pointing. As mentioned earlier, discontinuous models were originally proposed for handwriting where angular component can be discontinuous [70]. Three of the best performing models (namely discontinuous sigmoidal, asymmetric Gaussian, and MMMasym) are discontinuous at the peak of the speed profile. Fig. 7 shows a sample of the behavior of these models at the speed profile peak. This means that, in spite of superior mathematical fits, the piecewise-defined discontinuous functions are not realistic models of speed profile for wrist pointing movements. Imposing the conditions to ensure continuity and differentiability of these models at the peak may make these functions plausible models for speed profiles. However, these constraints are likely to significantly worsen goodness of fit in the least squares sense.

Fig. 7.

Sample fits for discontinuous models. Most fits of MMMasym, asymmetric Gaussian and discontinuous sigmoidal models show a discontinuity at the peak, which is not physiologically plausible for wrist pointing tasks.

Among the investigated models, the LGNB function displayed the best fitting performance. This function was previously used successfully to model drawing movements of unimpaired subjects [30] and also reaching and drawing movements of subjects recovering from stroke [38], [63]. Besides continuity, there are two properties that make LGNB a good modeling function: 1) its physiological grounding: As suggested by Plamondon, such function can be produced by convergence of actions of sets of linear neuromuscular subsystems operating in a cascade [67]–[69]. 2) Its flexibility: LGNB function’s asymmetry can be inverted by the change of a single parameter [30]. This is a valuable property since our experimental speed profiles exhibited both positive and negative skewness.

The beta function also displayed a good fitting performance. It was fourth overall on cumulative “Score 18” plot in Fig. 4(b), and second overall among continuous models. The good performance is consistent with the work of Krebs et al. [37], in which the beta function was successfully used to model speed profiles of submovements in shoulder and elbow movements of recovering stroke patients. Its properties make it particularly appealing for modeling submovements: by adjusting two parameters, its shape can be modulated to fit both symmetric and asymmetric speed profiles, as well as unimodal and bimodal profiles.¹ We also note that the mean values of skewness and kurtosis for the beta function models reported by Krebs et al. were similar to those for the speed profiles data recorded for our experiment: skewness = 0.07, kurtosis = 2.38 versus skewness = −0.07, kurtosis = 2.49.

Finally, our results provide a few insights on neural control of wrist pointing movements. Analysis of movement kinematic features has traditionally been used to infer control principles and variables used by the CNS to plan and generate movement. Specifically, the hypothesis that reaching movements is controlled in a hierarchical fashion with the kinematics on the top of this hierarchy has spurred from the analysis of movement “invariants” [26], [29] and, in particular, from the finding that trajectories are straight with bell-shaped profiles independent of the movement workspace. While the literature on wrist movement kinematics is still sparse, our results taken together with the recent findings by Charles and Hogan [74] afford some speculation on how the CNS may control wrist movements. Contrary to reaching, wrist trajectories are highly variable, consistent with the negligible role of interaction torques and the predominant role of stiffness in wrist dynamics [42]. Our results on speed profiles of wrist pointing movements showed, however, that these can be modeled in a similar way to highly stereotyped arm reaching movements; we were able to determine that the same models previously proposed for speed profiles of reaching or handwriting movements, including LGNB and beta, were also able to adequately model speed profiles of wrist movements (error within 4%). This result suggests that speed profile may be a key invariant for both arm and wrist movements. While human control of speed is known to be rather poor [28], we speculate that both arm and wrist movements may be instead generated under smoothness control, based on our findings that kurtosis of most of the normalized wrist speed profiles is > 2 with peak values around 2.3–2.5 (Fig. 3), i.e., kurtosis values are close to those associated with minimum-jerk speed profile (which is 7/3 or 2.33). While it is unclear which variables should be targeted by robot-mediated therapy to maximize motor recovery (e.g., accuracy, speed, smoothness), this finding suggests that therapy should be designed to maximize movement smoothness.

D. Applications to Rehabilitation Robotics

Applications of our results include design of control algorithms for therapeutic wrist robots for stroke treatment [35] and quantitative metrics of motor recovery including submovements [36], [37], [63], [80]. Our previous results suggest that sensorimotor training should target motions as opposed to muscles [22]. Building on this idea, for robot-mediated therapy of the shoulder and elbow [2] we achieved best clinical outcomes with “adaptive” therapies, where the robot assisted-as-needed subjects to meet kinematic specifications [35], [81]. During therapy, the performance-based adaptive controller guides the hand of the patient who aims poorly without holding him/her back and assists the other patient in making faster movements using a minimum-jerk profile of variable duration from the starting position to the ending position [35]. As we are expanding the performance-based algorithm to include therapies involving the distal limb segments, we have to determine whether the minimum-jerk profile is still appropriate or whether we should select a different model for the wrist movement kinematics. Specifically, our results will help us select reference models for wrist movement kinematics.

Taken together with state-of-the-art knowledge on neurorehabilitation of reaching movements, our results also suggest that upper limb robot-assisted therapies should target movement smoothness (see Section IV-C). Consistently, we recently found that, of the 20 robot-based metrics that were considered, smoothness was among the metrics that best correlated with therapy outcomes as measured by Fugl-Meyer and Motor Status scores [36]. Whether a robot-assisted therapy designed to maximize movement smoothness could yield to better results than therapies designed to target other variables is a testable hypothesis that could not only enhance stroke treatments efficacy but also improve our understanding of how the brain controls movement and recovers from injury.

V. Conclusion

This study aimed at identifying a model for speed profiles of fast, visually evoked, and visually guided wrist pointing movements. The performances of 19 models were assessed in terms of their ability to reconstruct our experimental data. The best fitting performances were obtained with continuous LGNB and beta functions and asymmetric, discontinuous models. In particular, the MMMasym model scored very high, probably due to its ability to describe curved trajectories. However, such models led to reconstructed profiles that were physiologically implausible. The strong performances of LGNB (best fitting), which has been highly used to model reaching movements and was found to be the best fitting model also in drawing movements, and beta function show that they may be suitable for wrist speed profiles modeling. While our most recent studies suggested that there may be significant differences between wrist pointing and arm reaching movements in terms of kinematics and motor control, this study showed that, at least for their speed profiles, they can be analyzed and modeled using similar tools. Applications of this study include the design of adaptive wrist robot controllers. Similar to reaching and handwriting modeling results, other applications include design of humanoid robots [82] and of robots that cooperate with humans [83], as well as systems for automatic signature verification [84], [85].

Biographies

Lev Vaisman received the B.A.Sc. degree in 2006 from the Engineering Science program and the M.A.Sc. degree in 2008 from the Institute of Biomaterials and Biomedical Engineering, both at University of Toronto, Toronto, ON, Canada, in 2006 and 2008, respectively. He is currently working toward the M.D.–Ph.D. degrees at Boston University School of Medicine, Boston, MA, USA.

His research interests are in rehabilitation engineering, cognitive neuroscience, and neural modeling.

Laura Dipietro, photograph and biography not available at the time of publication.

Hermano Igo Krebs (SM’04) joined the Mechanical Engineering Department, Massachusetts Institute of Technology, Cambridge, MA, USA, in 1997, where he is a Principal Research Scientist at the Newman Laboratory for Biomechanics and Human Rehabilitation. He also holds an affiliate position as an Adjunct Professor at the Department of Neurology, University of Maryland School of Medicine, and the Division of Rehabilitative Medicine. He is one of the founders of Interactive Motion Technologies, a startup developing robotics for rehabilitation. He is one of the pioneers of rehabilitation robotics and his goal is to revolutionize rehabilitation medicine by applying robotics to assist, enhance, and quantify rehabilitation. His efforts led to the American Heart Association to endorse in its 2010 guidelines for stroke care the use of robots for upper extremity rehabilitation. A similar endorsement was issued by the Veterans Administration later in that same year.

Appendix

Equations of Functions Used for Modeling

For all models P₁ … P_n are parameters, t₀ is the time movement started, t₁ is the time movement ended and t_m is the time when maximum velocity occurred. Abbreviations used in the plots and initial conditions are also shown.

Eden and Hollerbach Model (edhol) [30], [72] (P₁ = 9, P₂ = 1, P₃ = 0.5, P₄ = 1, P₅ = 4, P₆ = 3, P₇ = 0)

$$V=\{\begin{array}{ll}\sqrt{{\{P_{1}sin[{\mathrm{P}}_2(t-{\mathrm{P}}_3)]+{\mathrm{P}}_4\}}^2+{\{{\mathrm{P}}_{5}sin[{\mathrm{P}}_6(t-{\mathrm{P}}_7)]\}}^2},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}.\hfill \end{array}$$

Minimum Jerk Model (minjerk) [26], [30] (P₁ = 90, P₂ = 0, P₃ = 1)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{(t-{\mathrm{P}}_2)}^2{(t-{\mathrm{P}}_3)}^2,\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Minimum Snap Model (minsnap) [30], [65] (P₁ = −9, P₂ = 0, P₃ = 1)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{(t-{\mathrm{P}}_2)}^3{(t-{\mathrm{P}}_3)}^3,\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Morasso and Mussa-Ivaldi Minimum Acceleration Model (morasso) [29], [30] (P₁ = −90, P₂ = 0, P₃ = 1)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1(t-{\mathrm{P}}_2)(t-{\mathrm{P}}_3),\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Plamondon and Lamarche Model (expo) [30], [73] (P₁ = 180, P₂ = 0.5, P₃ = 0, P₄ = 9, P₅ = 5, P₆ = 1)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{e}^{-{\mathrm{P}}_2(t-{\mathrm{P}}_3)},\hfill & t_0\le t\le t_m\hfill \\ {\mathrm{P}}_4{e}^{-{\mathrm{P}}_5(t-{\mathrm{P}}_6)},\hfill & t_m\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Biexponential Model (biexpo) [47] (P₁ = 4.5, P₂ = 0.5, P₃ = 0.5)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{e}^{-\mid t-{\mathrm{P}}_2\mid /{\mathrm{P}}_3},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Plamondon Lognormal Model (lgn) [30] (P₁ = 9, P₂ = −1, P₃ = 10, P₄ = 1)

$$V=\{\begin{array}{ll}\frac{{\mathrm{P}}_1}{t-{\mathrm{P}}_2}{e}^{-{\mathrm{P}}_3{[ln(t-{\mathrm{P}}_2)-{\mathrm{P}}_4]}^2},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Plamondon Lognormal Model with Support Bound (lgnb) [30], [67] (P₁ = 45, P₂ = −1.5, P₃ = 1.5, P₄ = 2, P₅ = 0.5)

$$V=\{\begin{array}{ll}\frac{{\mathrm{P}}_1}{(t-{\mathrm{P}}_2)({\mathrm{P}}_3-t)}{e}^{-{\mathrm{P}}_4{[ln((t-{\mathrm{P}}_2)/({\mathrm{P}}_3-t))-{\mathrm{P}}_5]}^2},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Beta Function Model (beta) [30] (P₁ = 18, P₂ = −1, P₃ = 8, P₄ = 2, P₅ = 7)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{(t-{\mathrm{P}}_2)}^{{\mathrm{P}}_3}{({\mathrm{P}}_4-t)}^{{\mathrm{P}}_5},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Gamma Function Model (gamma) [30] (P₁ = 3.6, P₂ = −0.05, P₃ = 5, P₄ = 8)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{[{\mathrm{P}}_4(t-{\mathrm{P}}_2)]}^{{\mathrm{P}}_3}{e}^{-{\mathrm{P}}_4(t-{\mathrm{P}}_2)},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Weibull Model (weibull) [30] (P₁ = 108, P₂ = −0.25, P₃ = 5)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{[(t-{\mathrm{P}}_2)]}^{{\mathrm{P}}_3-1}{e}^{-{(t-{\mathrm{P}}_2)}^{{\mathrm{P}}_3}},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Sigmoidal Continuous Model (sigcont) [30] (P₁ = 90, P₂ = 0, P₃ = 2, P₄ = 4)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1\frac{t-{\mathrm{P}}_2}{{[1+{\mathrm{P}}_3(t-{\mathrm{P}}_2){\mathrm{P}}^4]}^2},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Sigmoidal Discontinuous Model (sigdiscont) [30] (P₁ = 18, P₂ = 0, P₃ = 1, P₄ = 7, P₅ = 54, P₆ = −0.2, P₇ = 1, P₈ = 8)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1\frac{t-{\mathrm{P}}_2}{{[1+{\mathrm{P}}_3(t-{\mathrm{P}}_2){\mathrm{P}}^4]}^2},\hfill & t_0\le t\le t_m\hfill \\ {\mathrm{P}}_5\frac{t-{\mathrm{P}}_6}{{[1+{\mathrm{P}}_7(t-{\mathrm{P}}_6){\mathrm{P}}^8]}^2},\hfill & t_m\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Gutman and Gottlieb Original Model (gg) [30] (P₁ = 180, P₂ = 0, P₃ = 0.5)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{(t-{\mathrm{P}}_2)}^2{e}^{-({(t-{\mathrm{P}}_2)}^3/{\mathrm{P}}_3)},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Gutman and Gottlieb Generalized Model (gggen) [30] (P₁ = 180, P₂ = −0.5, P₃ = 3, P₄ = 1)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{(t-{\mathrm{P}}_2)}^{{\mathrm{P}}_3-1}{e}^{-({(t-{\mathrm{P}}_2)}^{{\mathrm{P}}_3}/{\mathrm{P}}_4)},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Symmetric Plamondon Gaussian Model [30], [47] (symgauss) (P₁ = 27, P₂ = 0.5, P₃ = 0.5)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{e}^{-{((t-{\mathrm{P}}_2)/{\mathrm{P}}_3)}^2},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Asymmetric Plamondon Gaussian Model (asymgauss) [30] (P₁ = 27, P₂ = 0.5, P₃ = 0.5, P₄ = 27, P₅ = 0.5, P₆ = 0.5)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1{e}^{-{((t-{\mathrm{P}}_2)/{\mathrm{P}}_3)}^2},\hfill & t_0\le t\le t_m\hfill \\ {\mathrm{P}}_4{e}^{-{((t-{\mathrm{P}}_5)/{\mathrm{P}}_6)}^2},\hfill & t_m\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Symmetric Morasso, Mussa-Ivaldi and Maarse Model (mmmsym) [30], [64] (P₁ = 18, P₂ = −5, P₃ = −1)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1\{1-cos[{\mathrm{P}}_2(t-{\mathrm{P}}_3)]\},\hfill & t_0\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$

Asymmetric Morasso, Mussa-Ivaldi and Maarse Model (mmmasym) [30] (P₁ = 9, P₂ = −4, P₃ = 0, P₄ = 18, P₅ = −7, P₆ = −1)

$$V=\{\begin{array}{ll}{\mathrm{P}}_1\{1-cos[{\mathrm{P}}_2(t-{\mathrm{P}}_3)]\},\hfill & t_0\le t\le t_m\hfill \\ {\mathrm{P}}_4\{1-cos[{\mathrm{P}}_5(t-{\mathrm{P}}_6)]\},\hfill & t_m\le t\le t_1\hfill \\ 0,\hfill & \text{elsewhere}\hfill \end{array}.$$