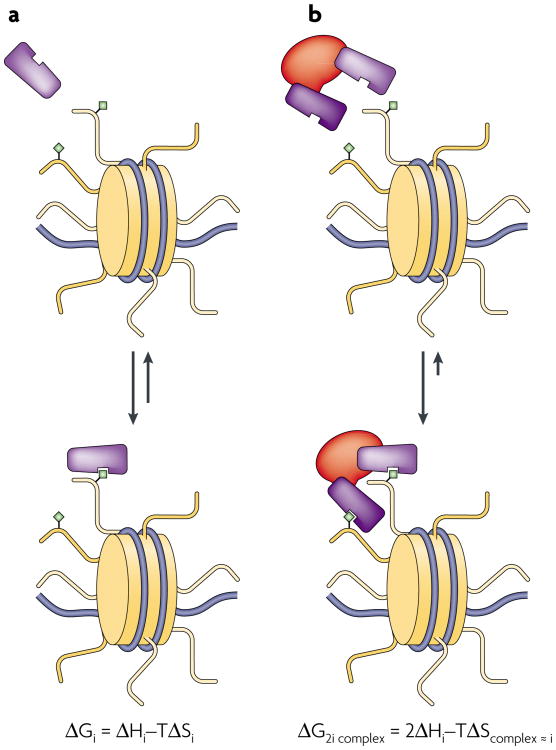
Figure 1. Thermodynamics of multivalent binding.

a | Monovalent association of a hypothetical effector module (purple) to a chromatin substrate (yellow tail with green diamond) is simplistically compared to a bivalent association of the same effector in a complex, representing the lowest order of multivalent interactions. The change in free energy ΔG_i for the monovalent system undergoing binding is indicated by the change in enthalpy ΔH_i minus the change in entropy ΔS_i, scaled by the temperature (T). b | By tethering the two effector modules, the entropy term may be, to a first approximation, similar for each of the binding equilibria in panels a and b (TΔS_complex ≈ TΔS_i). For our purposes, this example assumes that hydrogen-bonding electrostatic interactions dominate and desolvation is negligible, so that ΔS for the system will be negative. Thus, the entropic penalty to binding is lessened approximately twofold by pre-organizing the effector domains in a complex (TΔS_complex ≈ TΔS_i), while the enthalpy of the bivalent domain interaction is effectively double that of the monovalent case (∼2ΔH_i, if enthalpic penalties due to the strain induced by bivalent binding are negligible). In this manner, the reduced net entropy loss for the binding process can be a significant determinant of free energy, especially in low-binding enthalpy regimes. Losses of entropy on the substrate side would be expected to be minimal due to the low intrinsic rotational and translational freedom of chromatin; however, conformational entropy losses here are assumed to be negligible for simplicity.