Abstract
A common problem of interest within a randomized clinical trial is the evaluation of an inexpensive response endpoint as a valid surrogate endpoint for a clinical endpoint, where a chief purpose of a valid surrogate is to provide a way to make correct inferences on clinical treatment effects in future studies without needing to collect the clinical endpoint data. Within the principal stratification framework for addressing this problem based on data from a single randomized clinical efficacy trial, a variety of definitions and criteria for a good surrogate endpoint have been proposed, all based on or closely related to the “principal effects” or “causal effect predictiveness (CEP)” surface. We discuss CEP-based criteria for a useful surrogate endpoint, including (1) the meaning and relative importance of proposed criteria including average causal necessity (ACN), average causal sufficiency (ACS), and large clinical effect modification; (2) the relationship between these criteria and the Prentice definition of a valid surrogate endpoint; and (3) the relationship between these criteria and the consistency criterion (i.e., assurance against the “surrogate paradox”). This includes the result that ACN plus a strong version of ACS generally do not imply the Prentice definition nor the consistency criterion, but they do have these implications in special cases. Moreover, the converse does not hold except in a special case with a binary candidate surrogate. The results highlight that assumptions about the treatment effect on the clinical endpoint before the candidate surrogate is measured are influential for the ability to draw conclusions about the Prentice definition or consistency. In addition, we emphasize that in some scenarios that occur commonly in practice, the principal strata sub-populations for inference are identifiable from the observable data, in which cases the principal stratification framework has relatively high utility for the purpose of effect modification analysis, and is closely connected to the treatment marker selection problem. The results are illustrated with application to a vaccine efficacy trial, where ACN and ACS for an antibody marker are found to be consistent with the data and hence support the Prentice definition and consistency.
1 Introduction
An important goal of many biomedical research fields is identification of surrogate endpoints based on randomized clinical efficacy trials. With precise notation defined in Section 1.1, we have one randomized treatment (Z) for which two endpoints S and Y are both measured in each of the groups Z = 0 and Z = 1. S is an inexpensive study endpoint (typically a biomarker) measured shortly after randomization that is a candidate surrogate for the true clinical endpoint Y of interest. The primary objective of the trial is to learn about the treatment effect on Y, which is done by directly measuring P(y|Z). Where possible, future research of the same or similar treatments would proceed by additional randomized trials that also directly assess the treatment effect on Y. However, a valid surrogate endpoint S for Y can accelerate research to apply and develop effective treatments against Y, given that large resources are often required to directly measure P(y|Z) (e.g., taking several years of follow-up) and such assessment is often infeasible or unethical once moderately protective treatments are identified. Using the meaning surrogate = replacement, S is a valid surrogate for Y if in some sense measurement of P(s|Z) alone can inform us about P(y|Z), without needing to collect data on Y. This concept of a valid surrogate may be implemented in various ways, for example in terms of hypothesis testing, estimation, or both. For a perfect surrogate, P(s|Z) alone would provide the same information about P(y|Z) as if Y were measured along with S, for example providing a way to calculate the same point and confidence interval estimates of the treatment effect on Y. However, given the challenge in meeting this high bar the surrogate endpoint assessment literature has focused on learning something about P(y|Z) from P(s|Z) but not everything that would be learned by measuring P(y|Z) as well; for example the Prentice definition defines validity in terms of obtaining a valid hypothesis test of P(y|Z = 0) = P(y|Z = 1) based on P(s|Z) alone but does not consider estimation.
The term “surrogate” has been used for many objectives of biomarker research in clinical trials, and in our view it may be most clearly used for the “replacement endpoint” concept, thereby distinguishing surrogate/replacement endpoint assessment research from other biomarker assessment research. For example, as discussed below, studying biomarker-based subgroup effect modifiers of clinical treatment efficacy is useful for targeting treatments/interventions to subgroups where they will work and for selecting biomarker study endpoints for evaluating treatments in new Phase 1–2 trials. Biomarker response endpoints are also useful for exploring biological mechanisms of clinical treatment efficacy and for studying mediators of clinical treatment efficacy, which are distinct research activities with different objectives than surrogate/replacement endpoint evaluation.
Ideally, validation of a surrogate endpoint would be based on a synthesis of information from a large number of previous randomized trials of the same or similar treatments versus control where the surrogate and clinical endpoints were both measured [e.g., Gail et al. (2000) considers this approach]. However, it often occurs that data on the surrogate and clinical endpoint are available from only a single randomized trial, such that it is of interest to study definitions and criteria for useful surrogate and biomarker endpoints that are applicable for the identical setting as this single trial. While these definitions and criteria will be insufficient for validating surrogates or biomarkers for the ultimate goal of inferring clinical treatment effects of new treatments in the same or new setting, they are useful as a first step toward this objective and they aide clinical research in other ways that we discuss. We focus on the Prentice (1989) definition of a valid surrogate endpoint and on the principal stratification framework. This article is primarily about relating statements about the full-data distribution, although identifiability by the observed data distribution is also discussed and addressed in the application.
We state some of our conclusions up front. First, the literature discussing the utility of the Prentice (1989) surrogate framework has been inadequately clear in discriminating the Prentice definition (on obtaining a valid test of the null hypothesis of no clinical treatment effect from the surrogate alone) from criteria (e.g., conditions on the observed data distributions p(y|S,Z) and p(s|Z)) for checking the definition. The definition is clear and useful whereas the criteria, without modification, can be misleading and lead to disasters such as the surrogate paradox. For example, Frangakis and Rubin (2002) criticize a “statistical surrogate” defined as a biomarker satisfying a version of the Prentice (1989) criteria, which on the surface seems to criticize the whole Prentice framework but upon examination leaves the Prentice definition unscathed (e.g., the surrogate paradox cannot occur if the Prentice definition holds). We consider here the definition but not published operational criteria. In addition, while transportability of treatment effects via a surrogate endpoint is the paramount application of a surrogate as noted above, it is still useful to check the Prentice definition for the identical setting as the single trial, because it constitutes a first step/minimal bar for plausibility that the surrogate could also be used for estimating treatment effects in new settings.
Secondly, the principal stratification/principal surrogate framework does not in general provide a way to check the Prentice definition. We show that, depending on the problem context, principal stratification-based criteria can provide no discriminating information, partial discriminating information, or complete discriminating information about the Prentice definition. Therefore, the principal stratification framework has main utility for assessing whether and how treatment efficacy varies by subgroups defined by levels of biomarker response, thus being closely alighed with the utility of the treatment marker selection problem. In special cases, however, principal stratification criteria can establish the Prentice definition or one of its components specificity or sensitivity, and can also guarantee avoidance of the surrogate paradox (as illustrated in the application). In addition, the principal surrogate framework does fit the valid replacement endpoint concept, but in a different way than the Prentice definition. In particular, by providing a point and confidence interval estimate about clinical treatment efficacy for individuals based on their biomarker response values, it provides information about the clinical treatment effect for future subjects (from the same population) based on the biomarker endpoint alone without measurement of the clinical endpoint.
1.1 Set-Up of Randomized Trial for Assessing Clinical Efficacy
We consider a single clinical trial that randomizes n participants to active intervention (e.g., treatment or vaccine) versus a control intervention such as placebo, with Z the indicator of assignment to active intervention. Participants are followed for a fixed follow-up period for occurrence of the primary endpoint Y by time τ1 post-randomization, with Y the indicator of endpoint occurrence. For simplicity of exposition we assume no dropout during follow-up, though this could be accommodated straightforwardly under a random censoring assumption. Let S be the candidate surrogate endpoint measured at fixed time τ < τ1 post-randomization, which may be discrete or quantitative, and may be multivariate. Let R be the indicator that S is measured; frequently case-cohort, case-control, or two-phase sampling designs are used that only measure S in a judiciously chosen subset. Let Yτ be the indicator of primary endpoint occurrence before the time τ for measuring S. The observed random variables are (Z,R,RS,Yτ,Y). Lastly, let S(z), R(z), Yτ (z), and Y(z) be the potential outcomes if assigned treatment z, for z = 0,1, with W the vector of potential outcomes W ≡ (S(1),S(0),R(1),R(0),Yτ(1),Yτ(0),Y(1),Y(0)). We make the common assumptions for randomized clinical trials of SUTVA, ignorable treatment assignment (Z ⊥ W), the probability that S is missing in those with Yτ = 0 [i.e., P(R = 1|Yτ = 0)] depends only on observed data (missing at random assumption), and that the (Zi,Wi) are iid, for i = 1, n. The ignorable treatment assignment assumption will hold by design, and the missing at random assumption will hold by design if all subjects with Yτ = 0 contribute a viable sample for potentially measuring S at the visit at τ.
1.2 Background: Published Definitions and Criteria for a Principal Surrogate Endpoint
Joffe and Greene (2009) reviewed four frameworks for evaluating surrogate endpoints. The current article focuses on the principal stratification framework in comparison to the Prentice definition of a valid surrogate endpoint (Prentice, 1989) (but not to the Prentice criteria). Prentice stated his definition as “a response variable for which a test of the null hypothesis of no relationship to the treatment groups under comparison is also a valid test of the corresponding null hypothesis based on the true endpoint.” As stated in the first paragraph of the Introduction, S is a valid surrogate endpoint if measurement of P(s|Z) alone can inform us about P(y|Z), and the Prentice definition implements this concept in hypothesis testing but not in estimation. In particular, in our notation above a valid Prentice surrogate S satisfies P(Y(1) = 1) = P(Y(0) = 1) if and only if P(S(1) ≤ s1) = P(S(0) ≤ s1) for all s1, or, equivalently based on observable random variables given the trial is randomized, as P(Y = 1|Z = 1) = P(Y = 1|Z = 0) if and only if P(S ≤ s1|Z = 1) = P(S ≤ s1|Z = 0) for all s1. This if and only if statement allows the Prentice definition to be divided into two components of Specificity and Sensitivity, where Specificity means that no treatment effect on Y implies no treatment effect on S and Sensitivity means that a treatment effect on Y implies a treatment effect on S. In Section 3 we develop some criteria for separately checking Specificity and Sensitivity.
This article focuses on evaluating a candidate surrogate from a single randomized clinical trial, for evaluating its quality for the same setting as that trial. As such, within the frequency framework of statistics, satisfaction of the Prentice definition means that if the surrogate endpoint is used in an identical trial, then inference of the treatment effect on the surrogate is guaranteed to provide correct inference (in the dichotomous sense of correctly accepting or rejecting the null hypothesis) about the treatment effect on the clinical endpoint. While not directly relevant for answering the important question of whether the surrogate will be valid for a new treatment in the same or new setting, such a result is still useful because it provides indirect evidence that the surrogate would approximately satisfy the Prentice definition for a new treatment if the treatment is similar to the original treatment (e.g., in the same drug class). If two candidate surrogates are assessed in a single efficacy trial and one satisfies the Prentice definition and one does not, then it may be rational to prioritize the Prentice surrogate as a study endpoint in subsequent Phase I/II trials of new and similar treatments that will constitute the basis for selecting the most promising new treatment to advance to the next efficacy trial.
Several papers have considered definitions and criteria for a useful principal surrogate endpoint. Within the potential outcomes framework of causal inference, Frangakis and Rubin (2002) defined S to be a principal surrogate if every individual with a causal treatment effect on the clinical endpoint Y also has a causal treatment effect on the surrogate S (i.e., “causal necessity”). This definition states that a valid surrogate satisfies P(Yi(1) = 1) = P(Yi(0) = 1) for all subjects i with Si(1) = Si(0), which departs from the Prentice definition in 1) being required for all individuals and in 2) being unidirectional (instead of if and only if). Gilbert and Hudgens (2008), focusing on what could be evaluated from the sampling scheme of a typical randomized trial, modified the causal necessity condition to “average causal necessity” (ACN), i.e., no average causal treatment effect on Y in the sub-population with S(1) = S(0) and Yτ(1) = Yτ (0) = 0; the latter condition was added to ensure that causal treatment effects on S are defined. ACN can be expressed in terms of the “principal effects” or “causal effect predictiveness” (CEP) surface, which is defined in terms of the clinical risks under each treatment assignment,
With h(x,y) a known contrast function satisfying h(x,y) = 0 if and only if x = y, for example h(x,y) = x – y, the CEP surface is defined as
and ACN is expressed as CEP(s1,s0) = 0 for all s1 = s0. Gilbert and Hudgens (2008) defined S to be a principal surrogate if ACN and average causal sufficiency (ACS) hold, where a 1-sided version of ACS (relevant for active treatment versus control trials considered here) states that there exists a constant C ≥ 0 such that the subgroup of subjects with a sufficient treatment effect on S, those with {S(1) = s1,S(0) = s0 with s1 – s0 > C}, has a beneficial causal effect on Y, i.e., CEP(s1,s0) has the sign indicating benefit. We refer to 1-sided ACS with C = 0 as 1-sided strong ACS; note that for a biomarker satisfying ACN plus 1-sided strong ACS, the subgroup with no individual causal effect on S has zero clinical treatment effect and the subgroup with positive individual causal effect on S has a beneficial clinical treatment effect. Thus Gilbert and Hudgen's (2008) definition of a strong (C = 0) 1-sided principal surrogate can be stated as P(Y(1) = 1|S(1) = S(0),Yτ(1) = Yτ(0) = 0) = P(Y(0) = 1|S(1) = S(0),Yτ(1) = Yτ(0) = 0) and P(Y(1) = 1|S(1) > S(0),Yτ (1) = Yτ (0) = 0) < P(Y(0) = 1|S(1) > S(0),Yτ(1) = Yτ(0) = 0).
Moreover, both Frangakis and Rubin (2002) and Gilbert and Hudgens (2008) expressed the concept that studying the whole CEP surface is important for evaluating the utility of a candidate principal surrogate; the former authors expressed this by stating that a more useful biomarker will have relatively more associative than dissociative effects, whereas the latter authors expressed this by stating that a more useful biomarker will have wide variability in the CEP surface over subgroups defined by (S(1),S(0)), i.e., the biomarker is a strong effect modifier.
The marginal CEP curve causal parameter, closely related to the CEP surface, is also useful for evaluating a principal surrogate, which contrasts the risks averaged over the distribution of S(0): mCEP(s1) ≡ h(mrisk1(s1),mrisk0(s1)), where
While ACN and ACS are not in general defined for this causal parameter, the “wide variability/strong effect modifier” principal surrogate criterion is operable, and identifiability is achieved under weaker assumptions (Wolfson and Gilbert, 2010). Below we consider both the CEP and mCEP full-data causal parameters as useful quantities for evaluating and understanding principal surrogate quality.
Our results below use an additive difference contrast h(x,y) = x – y, with advantage that, under EECR defined below and a no-harm monotonicity assumption [P(Y(1) = 1,Y(0) = 0) = 0], –CEP(s1,s0) has interpretation as a conditional probability of the disease being averted by assignment to Z = 1: –CEP(s1,s0) = P(Y(1) = 0,Y(0) = 1|S(1) = s1,S(0) = s0,Yτ(1) = Yτ(0) = 0); similarly –mCEP(s1) = P(Y(1) = 0,Y(0) = 1|S(1) = s1,Yτ(1) = Yτ(0) = 0). Other principal surrogate evaluation literature has considered the CEP surface (Zigler and Belin, 2012) or closely related causal parameters. Taylor, Wang, and Thiebaut (2005) studied the proportion associative (PA) summary measure of principal surrogate value,
which is the proportion of the study population with a beneficial clinical effect that also has a positive surrogate effect. (This definition assumes no clinical events before τ.) With the additive difference contrast h(x,y) = x – y and no-harm monotonicity defined above, straightforward calculation shows that PA = ∫s1 > s0 CEP(s1,s0) dP(s1,s0)/CE, where P(s1,s0) is the joint cdf of S(1) and S(0) conditional on Yτ(1) = Yτ(0) = 0 and CE ≡ h(P(Y(1) = 1),P(Y(0) = 1)) is the overall clinical treatment effect. For the special case of binary S, Li, Taylor, and Elliott (2010) studied the 16 causal parameters constituting the joint distribution of (S(1),S(0)) and (Y(1),Y(0)). Under the same assumptions given above, these parameters for Y(1) = 0 and Y(0) = 1 map to the CEP surface: P(S(1) = s1,S(0) = s0,Y(1) = 0,Y(0) = 1) = CEP(s1,s0)P(s1,s0)/CE for (s1,s0) ∈ {0,1}.
Additional work clarified the value or limitations of the above criteria for a biomarker's utility as a principal surrogate, and suggested new criteria. Vander-Weele (2011) showed that ACN can hold yet the treatment has a causal effect on Y not mediated through S. For example, this situation may occur if there are two independent biological mechanisms of clinical protection, one that operates directly through S and one that does not. On the positive side for ACN, VanderWeele (2011) also showed that failure of ACN does imply that the treatment has a causal effect on Y not mediated through S; thus ACN is a valid criterion to ‘disprove’ full mediation but cannot affirm it. (Thus Frangakis and Rubin's (2002) principal surrogate definition is about a one-way implication, different from the if and only if implications of the Prentice definition.) In addition, Gilbert, Hudgens, and Wolfson (2011) emphasized that, for the purpose of iteratively developing increasingly efficacious treatments, ACN and ACS may be less important for a useful principal surrogate than the strong effect modifier criterion that CEP(s1,s0) widely varies across subgroups defined by (s1,s0). Strong effect modification may occur in many ways not implying ACN nor ACS, and strong effect modification alone, combined with an overall beneficial clinical treatment effect implies that there is at least one subgroup with relatively large clinical efficacy. Strong effect modification “sets the target” for future development of improved treatments, where the goal is to find refined treatments that generate S in the “high efficacy zone” for a greater percentage of active treatment recipients; combining these data results with context-dependent bridging assumptions [e.g., Pearl and Bareinboim (2011) initiated a framework for combining data with bridging assumptions] would predict that the refined treatment would confer greater overall clinical efficacy. One way that wide variability could lead to erroneous bridging for improving a treatment would be if new subjects added to the high efficacy zone by the new treatment have a different distribution of clinical effect modifiers than the subgroup in the high efficacy zone in the original trial. Nevertheless, wide variability is a useful criterion for research areas that study a battery of biomarker endpoints as potential surrogates; this criterion may be used for prioritizing/ranking the biomarker endpoints to use in Phase I/II trials for comparing refined treatments and for selecting the most promising treatments to advance to the next efficacy trial.
Another criterion for a good surrogate endpoint is the original Prentice (1989) definition of a valid replacement endpoint for the clinical endpoint, and below we provide results on the implications of ACN + 1-sided strong ACS on the Prentice definition and vice versa. The results show how the implications depend on assumptions about causal treatment effects on the clinical endpoint before and after the biomarker is measured. These implications yield alternative criteria to the original Prentice criteria for checking the Prentice definition of a valid surrogate endpoint.
Many authors including Chen, Geng, and Jia (2007), Ju and Geng (2010), and VanderWeele (2013) rightly assert that a reasonable surrogate endpoint should be assured to avoid the “surrogate paradox” pitfall, defined as the scenario where the effect of the treatment on the surrogate is positive, the surrogate and clinical outcomes are positively correlated, yet the overall clinical treatment effect CE indicates harm by the active treatment. Below we note scenarios, which commonly occur in practice, for which ACN plus 1-sided strong ACS guarantee a “consistent surrogate” (defined as the surrogate paradox cannot happen).
The remainder of this article is organized as follows. Section 2 clarifies that principal surrogate analysis is essentially subgroup effect modification analysis. Section 3 provides results on ACN and 1-sided ACS as criteria for checking the Prentice surrogate definition. Section 4 provides results on these criteria for checking a consistent surrogate. Section 5 illustrates the relationships with a Zoster vaccine efficacy trial, Section 6 provides discussion, and the appendix contains proofs of results.
2 Principal Surrogate Assessment: Subgroup Effect Modification Analysis
2.1 Connection to the Treatment Marker Selection Problem
Principal surrogate analysis is subgroup analysis (hence suggesting a name such as principal stratification effect modification analysis), with objective to characterize how clinical treatment efficacy varies over subgroups, where these subgroups are defined by post-randomization principal strata (which by construction may be treated as baseline covariates) and possibly also by actual baseline covariates. The analysis essentially repeats the overall intention-to-treat analysis for each of a range of these subgroups, assessing the effect of treatment assignment on disease risk within each subgroup, and, like the overall analysis, provides little or no direct information about mechanisms or mediators of protection. As such, the principal surrogate problem has a close connection with the “treatment marker selection problem,” which has goal to determine if and how clinical treatment efficacy varies over subgroups defined by biomarkers measured at baseline [e.g., Huang, Gilbert, and Janes (2012)]. While the statistical approaches for these two problems are highly related, the applications are partly overlapping and partly distinct; for instance both fields seek to rank biomarker endpoints by their strength of effect modification and hence utility for treatment development, but, unlike the treatment marker selection field that often focuses on individual decision-making for tailored allocation of therapy, the principal surrogate field has focused on different applications including the prediction of overall treatment efficacy from the biomarker distribution in a similar or new setting (Follmann, 2006; Huang, Gilbert, and Wolfson, 2013). In addition, the treatment marker selection field does not endeavor to identify “perfect or “valid” treatment selection markers; rather it focuses on characterizing efficacy over subgroups and the ranking of biomarkers by the strength of effect modification. Similarly, principal surrogate evaluation is primarily about comparing candidate surrogates and ranking them by the degree of their utility as effect modifiers, and the field should not be dominated by the objective to identify perfect/valid surrogates. Nevertheless, the joint criterion of ACN together with strong ACS has particular value in checking the Prentice definition or the individual components of the Prentice definition as described below.
The analogy with the treatment marker selection literature also suggests that if very strong baseline effect modifiers exist, then it may be unimportant to develop a biomarker response effect modifier– one can simply predict clinical treatment effects based on actual baseline variables, avoiding the identifiability challenges of the principal stratification framework (Ross Prentice has voiced this point). While true, in practice a response to treatment may be a stronger effect modifier, motivating principal surrogacy assessment, and many such examples exist. The analogy also raises the question as to when the principal strata subgroups are identifiable from the observable data, as an affirmative answer to this question places the principal stratification problem much closer to the treatment marker selection problem where subgroups are obviously directly observable.
2.2 Is the Principal Stratum for Inference Observable?
A key issue for the utility of principal stratification research in general is whether the principal stratum for inference is observable versus latent and never observable. Many principal strata of interest in a variety of applications are not observable, rendering the approach un-helpful for decision-making for individual patients or for health policy [e.g., Joffe (2011)]. However, for present application there is a special case where the principal stratum for inference is identifiable from the observable data, the “Constant Biomarker scenario (i.e., the conditional distribution S(0)|Yτ (0) = 0 is degenerate), which has been considered in several papers. In Case CB the CEP surface collapses to the mCEP curve, and ACN and ACS may be assessed based on the mCEP curve. Case CB is important because the principal strata subgroups are specified by {S(1) = s1,Yτ(1) = Yτ(0) = 0}, which are identifiable (equating to {S(1) = s1,Yτ(1) = 0}) under the no early-protection monotonicity assumption P(Yτ(1) = 0, Yτ(0) = 1) = 0. Where this assumption fails, the principal strata subgroups will be approximately equal to the identifiable subgroups if at most a very small subgroup receives clinical protection by τ, which is especially likely to hold if the rate of disease by τ is much less than the rate of disease after τ.
While Case CB has been motivated by vaccine efficacy trials, it also may occur in general active treatment versus control randomized trials with S defined as the difference in a biomarker readout between time τ and the time of randomization (Gabriel and Gilbert, 2014). In this scenario, if τ is reasonably close to baseline and the passage of time from baseline to τ is not expected to alter the biomarker during that time for subjects assigned Z = 0, then it may be reasonable to set S(0) = 0 for all subjects. While in many applications the measured differences S may have some variability about 0, sometimes this scatter may be assumed to be random measurement error, in which case it is of interest to assess the ‘de-noised’ variable S as a principal surrogate that does have S(0) = 0 for all subjects. Another advantage of this “difference biomarker” scenario is that the baseline biomarker may be predictive of S, which aides identifiability and efficiency of estimation of the CEP surface and mCEP curve via the baseline immunogenicity predictor (BIP) augmented trial design (Follmann, 2006; Gilbert and Hudgens, 2008; Qin et al., 2008; Huang and Gilbert, 2011; Huang, Gilbert, and Wolfson, 2013; Long and Hudgens, 2013, Gabriel and Gilbert, 2014).
In sum, if the principal strata subgroups are identifiable from observable random variables, then principal stratification effect modification assessment has utility similar to baseline covariate subgroup analysis of effect modification, whereas otherwise, the utility is reduced, but still present for the purposes of ranking candidate biomarkers and for providing inputs into bridging formulas for predicting overall treatment efficacy.
3 Connection of ACN and 1-Sided ACS with the Prentice Definition of a Valid Surrogate Endpoint
3.1 Prentice Definition
A criterion for a good principal surrogate endpoint is satisfaction of Prentice's (1989) definition as a valid replacement endpoint for the clinical endpoint. This definition may be expressed as perfect population-level specificity and sensitivity of the surrogate. Henceforth we use h(x,y) = x – y such that CE = P(Y(1) = 1) – P(Y(0) = 1) and CE < 0 indicates clinical benefit, and CEP(s1,s0) = risk1(s1,s0) – risk0(s1,s0).
We define 2-sided and 1-sided versions of Specificity and Sensitivity as follows:
We use the contrapositive forms of 2-Sided Specificity and 1-Sided Specificity to distinguish them: S(1) ≠d S(0) ⇒ CE ≠ 0 and S(1) >st S(0) ⇒ CE < 0, respectively. In the above definitions >st indicates stochastically larger, i.e., S(1) >st S(0) means that P(S(1) > s) ≥ P(S(0) > s) for all s with > for at least one s. Because CE is an intention-to-treat parameter, in the above definitions we include “undefined” (*) as one of the values of S, such that S(1) =d S(0) means that P(S(1) ≤ s) = P(S(0) ≤ s) for all defined s and P(S(1) = *) = P(S(0) = *), where this last equality is equivalent to no early average clinical treatment effect P(Yτ(1) = 1) = P(Yτ(0) = 1).
Specificity means that rejecting the null hypothesis of no treatment effect on the surrogate implies a treatment effect on the clinical endpoint (CE ≠ 0 or a one-sided version), whereas Sensitivity means that accepting the null hypothesis of no treatment effect on the surrogate implies no treatment effect on the clinical endpoint (CE= 0).
3.2 Overall Clinical Efficacy Averaged Over the CEP Surface
Criteria for checking Specificity and Sensitivity may be derived solely based on observable random variables, without the need for potential outcomes, following Prentice (1989) and subsequent work. However, in this work we study the relationship of Specificity and Sensitivity to ACN and 1-sided ACS, which requires potential outcomes notation. In Section 5 we provide an example where principal stratification effect modification analysis supports ACN + 1-sided strong ACS for a biomarker endpoint, generating the question of what does this imply about whether Specificity and/or Sensitivity hold? As a preliminary step, we partition CE as a weighted average of the CEP surface across subgroups. The results are developed for the additive difference contrast function h(x,y) = x–y; additional research would be needed for alternative contrasts. For concreteness in the following results we suppose S is discrete with J levels {0,···,J – 1} (in addition to the level S = *). While we present the results for discrete S, they carry over to the case of continuous S by replacing sums with integrals.
Define P(s1,s0) ≡ P(S(1) = s1,S(0) = s0|Yτ (1) = Yτ (0) = 0) for (s1,s0) ∈ {0,···,J – 1} × {0,···,J – 1}, P*(j,k) = P(Yτ(1) = j,Yτ(0) = k) for j,k ∈ {0,1} × {0,1}, and for j = 0,1. We refer to the subgroups defined by {Yτ(1) = 0,Yτ(0) = 0}, {Yτ(1) = 0,Yτ(0) = 1} and {Yτ(1) = 1,Yτ(0) = 0} as the early-always-at-risk, early-protected and early-harmed principal strata, respectively. In addition, define
Throughout we assume P*(0,0) > 0, which should be safe to assume in almost all meaningful applications for evaluating a surrogate endpoint. We state a result for easy reference in the forthcoming results.
CE Decomposition
| (1) |
| (2) |
| (3) |
| (4) |
The above decomposition is useful for judging the utility of ACN, ACS, and wide variability in CEP(s1,s0) as criteria for a useful biomarker. In general we wish for high power to reject H0 : CE ≥ 0 in favor of a beneficial clinical treatment effect H1 : CE < 0. If ACN holds, then by equation (1)–(4), for a biomarker to correctly reflect a ‘big’ overall clinical treatment effect, we need -CEP(s1,s0) large when P(s1,s0) is large. This equation indicates that for developing highly efficacious treatments, there is nothing essential about ACS; what is needed is large -CEP(s1,s0) for some subgroups defined by {S(1) = s1,S(0) = s0,Yτ(1) = Yτ(0) = 0} and the ability of an improved treatment to generate large subgroups of this kind. It also indicates that ACN is not essential either; this is related to the comment above on the limitation of ACN that it does not imply full mediation. Therefore, strong effect modification/wide variability of CEP(s1,s0) is a more important criterion for developing new treatments than ACS and even ACN, and greater attention to criteria for valid bridging to new subgroups is needed (Pearl and Bareinboim, 2011); the latter issue is paramount but beyond the scope of this article.
The overall efficacy CE is a weighted average of the CE( j,k) for the early always-at-risk, early-protected, and early-harmed principal strata, with weights P*(0,0), P*(0,1), and P*(1,0). The P*(j,k) are not identifiable from the observed data without assumptions about early clinical treatment effects, but with ENHM defined below they are identified, with and .
3.3 Results on the Relationship of ACN and 1-Sided ACS to Specificity and Sensitivity
We consider a menu of assumptions that will be selected from to infer results.
Equal Early Clinical Risk (EECR)
P(Yτ(1) = Yτ (0)) = 1, i.e., treatment has no early clinical effect for any individual
Early No-Harm Monotonicity (ENHM)
P*(1,0) ≡ P(Yτ(1) = 1,Yτ(0) = 0) = 0, i.e., treatment does not cause early harm for any individual (the early-harmed subgroup is empty)
Population Early Monotonicity (PEM)
CE(1,0)P*(1,0)+ CE(0,1)P*(0,1) = P(Y(1) = 1,Yτ(1) ≠ Yτ(0)) – P(Y(0) = 1,Yτ(1) ≠ Yτ(0)) ≤ 0, i.e., the union of the early-protected and early-harmed subgroups does not have population-level clinical harm
No Negative Marker Effects (NNMEs)
P(S(1) ≥ S(0)|Yτ(1) = Yτ (0) = 0) = 1, i.e., active treatment versus control does not reduce the biomarker for any individual in the early-always-at-risk subgroup
Monotonicity
CEP(s1,s0) ≤ 0 for all subgroups defined by biomarker levels {S(1) = s1,S(0) = s0} ∈ {0,···,J – 1} × {0,···,J – 1}, i.e., treatment does not cause harm for any individual in the early-always-at-risk subgroup
Case CB
P(S(0) = 0) = 1
The following results attain, with proofs in the appendix. For these results we re-define ACN and 1-sided ACS slightly as follows. ACN is CEP(s1,s1) = 0 for all s1 with P(s1,s1) > 0 and 1-sided ACS is CEP(s1,s0) < 0 for all s1 – s0 > C and P(s1,s0) > 0. The results are organized by the strength of the assumption about early clinical treatment effects, from strongest to weakest.
Result 1 (Under EECR)
EECR + ACN + Case CB imply Sensitivity. Conversely, EECR + Sensitivity + Case CB imply ACN. Apart from Case CB, EECR + ACN do not imply Sensitivity and EECR + Sensitivity do not imply ACN, even under all four of the extra assumptions PEM + NNMEs + Monotonicity + Case CB.
EECR + ACN + 1-sided strong ACS imply Specificity under any of NNMEs, Monotonicity, or Case CB. Conversely, EECR + Specificity + Sensitivity do not imply 1-sided ACS for any C ≥ 0, even under all four of the extra assumptions.
Result 2 (Under ENHM)
ENHM + ACN do not imply Sensitivity even under all four of the extra assumptions. Conversely, ENHM + Sensitivity + Monotonicity + Case CB imply ACN.
Similar to Result 1, ENHM + ACN + 1-sided strong ACS imply Specificity under any of NNMEs, Monotonicity, or Case CB, whereas ENHM + Specificity + Sensitivity do not imply 1-sided ACS for any C ≥ 0 even under all four of the extra assumptions.
Result 3 (General)
ACN does not imply Sensitivity even under all four of the extra assumptions. Conversely, Sensitivity + PEM + Monotonicity + Case CB imply ACN.
ACN + 1-sided strong ACS + PEM imply Specificity under any of NNMEs, Monotonicity, or Case CB. As for Results 1 and 2, Specificity + Sensitivity do not imply 1-sided ACS for any C ≥ 0 even under all four of the extra assumptions.
Results 1 and 2 show that the principal surrogate conditions can be used to check the two parts of the Prentice definition. They show that EECR + Case CB are needed for inferring the full Prentice definition from ACN and 1-sided strong ACS, where relaxing either one loses the implication. Results 1 and 2 also show the importance of EECR for the principal surrogate criteria to have implications on the Prentice definition (required for inferring Sensitivity), even under all four extra assumptions PEM, NNMEs, Monotonicity, and Case CB. Results 1 and 2 also show that the Prentice definition does not imply ACS even under many possible assumptions; the basic reason is that there are many ways for CE ≠ 0 with CEP(s1,s0) zero for some s1 ≠ s0 and below zero for other s1 ≠ s0.
A useful application of Result 3 is that in general applications where PEM and NNMEs or Monotonicity hold (which is often plausible), if the estimated vaccine efficacy curve takes the classic shape of being near zero at s1 = 0 (supporting ACN) and rising above zero for positive values s1 > 0 (e.g., as in our example illustrated in Figure 2), then one may conclude Specificity. That is, a classic vaccine efficacy curve indicates that an inference of beneficial overall vaccine efficacy follows from the observation that vaccine recipients tend to have higher biomarker responses than placebo recipients.
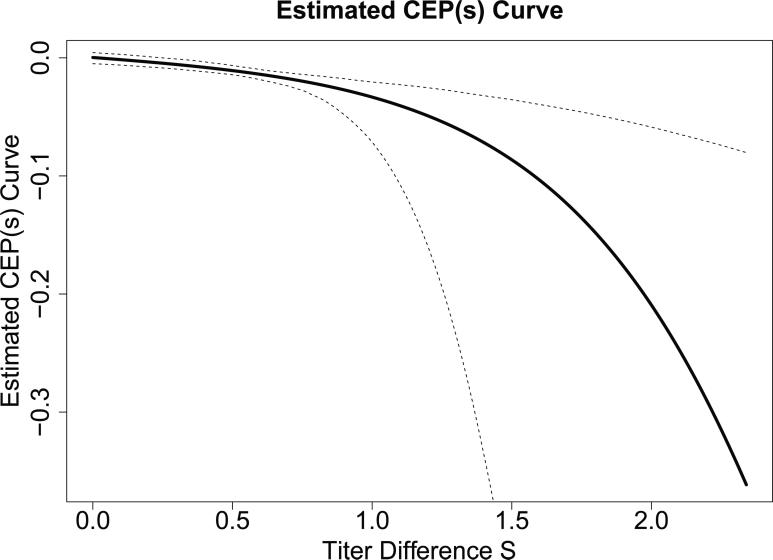
Figure 2.
Point and 95% confidence interval estimates of the CEP curve, CEP(s1) ≡ CEP(s1,0) = risk1(s1,0) – risk0(s1,0), for the ZEST data with candidate surrogate S the log10 fold-rise of gpELISA antibody titers from baseline to week 6. The Weibull estimated maximum likelihood method of Gabriel and Gilbert (2014) was used, assuming a parametric normal model for S(1) conditional on the BIP X and using the clinical endpoint Y = I[T ≤ t] for t = 2 years.
Next we state Result 1 for the special case that S is binary. The results on implications of ACN and ACS for Sensitivity and Specificity are unchanged, whereas the reverse implications are strengthened. In contrast, Results 2 and 3 are unchanged for S binary compared to S categorical with more than two categories.
Result 1-Binary (Binary S Under EECR)
In the special case of S binary and EECR + Case CB, ACN implies Sensitivity and Sensitivity implies ACN. In addition ACN plus 1-sided strong ACS imply Specificity and Sensitivity + Specificity imply 1-sided strong ACS.
Result 1-Binary shows that EECR + Case CB + S binary constitutes a scenario where both principal surrogate conditions hold if and only if the Prentice definition holds. For a binary S the Prentice definition does not have implications on ACS if EECR is relaxed, however, further highlighting the importance of EECR.
3.4 Results Under Minor Violations of Case CB and EECR
In the example described in Section 5, there may be minor violations of the Case CB and EECR assumptions, raising the question of whether the results are approximately correct under such violations. We state a variant version of Result 1 to address this question with proof in the appendix, and note that the other results have similar properties under minor violations. We use the following extension of the notation.
Define Case CB-ε as P(S(0) > 0) = ε for ε a small positive constant, EECR-ε as P(Yτ(1) ≠ Yτ(0)) = ε, ENHM-ε as P(Yτ(1) = 1,Yτ(0) = 0) = ε, Sensitivity-ε as S(1) =d S(0) ⇒ CE → 0 as ε → 0, 1-sided Specificity-ε as S(1) >st S(0) ⇒ CE → c as ε → 0 for some negative constant c, ACN-ε as CEP(s1,s1) → 0 as ε → 0 for all s1 ∈ {0,···,J – 1}, and ACN-ε(0,0) as CEP(0,0) → 0 as ε → 0.
Result 4 (Result 1 Under Minor Violations of Case CB and EECR)
EECR + ACN-ε + Case CB-ε imply Sensitivity-ε. Conversely, EECR + Sensitivity-ε + Case CB-ε imply ACN-ε(0,0) but not ACN-ε. EECR + ACN-ε + 1-sided strong ACS imply Specificity-ε under any of NNMEs, Monotonicity, or Case CB-ε. The same implications hold replacing EECR with EECR-ε.
Result 4 implies that the principal stratification criteria do correctly check the Prentice definition under minor violations converging to zero in that Sensitivity-ε and Specificity-ε hold when Case CB is relaxed to Case CB-ε and EECR is relaxed to EECR-ε. In addition, while Result 4 shows that the Prentice definition does not imply ACN-ε if Case CB is minorly violated, it shows that the Prentice definition does imply ACN-ε(0,0), which may be what matters in practice given that the principal stratum {S(1) = S(0) = 0} constitutes the only causal necessity principal stratum containing study subjects as ε → 0. See the appendix for a proof of Result 4.
Result 2 extends to a result where ENHM-ε + Sensitivity-ε + Monotonicity + Case CB-ε imply ACN-ε and ENHM-ε + ACN-ε + 1-sided strong ACS imply Specificity-ε under any of NNMEs, Monotonicity, or Case CB-ε. Result 3 extends to a result where Sensitivity-ε + PEM + Monotonicity + Case CB-ε imply ACN-ε. Result 1-Binary extends to a result where, for S binary and assuming EECR-ε + Case CB-ε, ACN-ε implies Sensitivity-ε and Sensitivity-ε implies ACN-ε(0,0) but not ACN-ε; moreover ACN-ε plus 1-sided strong ACS imply Specificity-ε and Sensitivity-ε + Specificity-ε imply 1-sided strong ACS.
3.5 Interpretation and Testability of the Assumptions
The first two assumptions EECR and ENHM are about the effect of treatment on Y before the biomarker is measured. The stronger assumption EECR assumes no effect for any individual, and has been used for all but one paper on evaluating a principal surrogate, given the great help it provides toward identifying the CEP surface and the marginal CEP curve. Wolfson and Gilbert (2010) considered sensitivity analysis methods that relax EECR to ENHM or to no assumption about early treatment effects. EECR and ENHM are not fully testable but have testable implications; e.g., they can be rejected by finding early clinical treatment effects overall or in subgroups.
PEM is only relevant if EECR fails, as under EECR P*(1,0) = P*(0,1) = 0, such that CE(1,0) and CE(0,1) are irrelevant, as treatment effects in empty subgroups. There are no obvious testable implications of PEM. It holds under the no-harm monotonicity assumption considered above. Without this monotonicity assumption, it may be relatively plausible in settings where the early-protected subgroup is much larger than the early-harmed subgroup and there is reason to expect that the early-protected also receive some later protection. NNMEs will be plausible in many active versus control trials, and can be partially checked by comparing the distributions of S(1)|Yτ(1) = 0 and S(0)|Yτ(0) = 0. Monotonicity will be more plausible in settings with higher overall efficacy and can be partially checked similarly to checking ENHM. Case CB can be checked by examining the distribution of S(0)|Yτ(0) = 0.
4 Connection of ACN and 1-Sided ACS with Verifying a Consistent Surrogate
As argued by several authors including Fleming and DeMets (1996), Chen et al. (2007), Ju and Geng (2010), and VanderWeele (2013), a good surrogate endpoint should be assured to avoid the “surrogate paradox” pitfall, defined as the scenario where the treatment effect on the surrogate is positive (i.e., S(1) >st S(0)), the surrogate and clinical outcomes are positively correlated (i.e., S(z)|Y(z) = 0,Yτ(z) = 0) >st S(z)|Y(z) = 1,Yτ (z) = 0 for each z = 0,1), yet the overall clinical treatment effect CE is harmful (CE > 0). For scenarios that commonly occur in practice, examination of the CEP surface immediately establishes that ACN plus 1-sided strong ACS defined above guarantee that the surrogate paradox cannot occur, i.e., the surrogate is consistent. In particular, under EECR, ACN plus 1-sided strong ACS guarantee a consistent surrogate if any of NNMEs, Monotonicity, or Case CB hold. Under ENHM, these same conditions imply a consistent surrogate if PEM is added to the set of assumptions. If ENHM is also relaxed, then no combination of these conditions imply a consistent surrogate. As also discussed by VanderWeele (2013), while the principal stratification framework provides criteria for a consistent surrogate, the fundamental challenge to its implementation is ensuring valid estimation of the CEP surface given identifiability challenges. (Identifiability assumptions are discussed extensively in the literature.)
5 Application to the ZEST
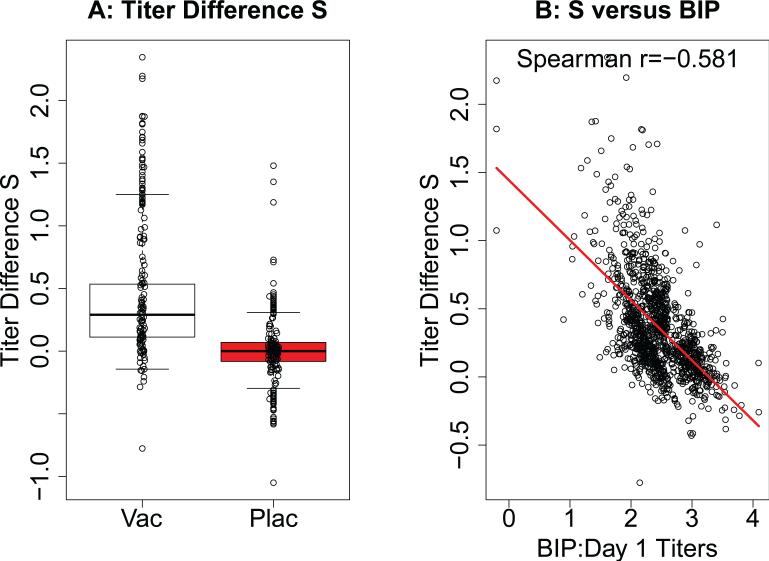
We apply the above results to the Phase 3 Zostavax Efficacy and Safety Trial (ZEST), which randomized 22, 439 North American and European subjects aged 50–59 years in a 1:1 allocation to receive attenuated Zoster vaccine (ZV or Zostavax; Merck & Co., Whitehouse Station, NJ) or placebo, with primary objective to assess the vaccine efficacy to prevent herpes zoster (HZ). Schmader et al. (2012) reported an estimated overall vaccine efficacy of 69.8%, using a one minus relative risk (vaccine/placebo) estimand multiplied by 100%. Here we focus on the additive difference estimand CE ≡ P(Y(1) = 1) – P(Y(0) = 1), obtaining an estimated CE of -0.0065 with 95% confidence interval −0.0093 to −0.0037 and 2-sided p < 0.001 for CE being different from zero. A study objective was to assess varicella zoster virus (VZV) antibody titers measured by gpELISA as a surrogate endpoint for HZ. A variety of principal surrogate analyses have been performed to evaluate various VZV-antibody based candidate surrogates (Miao et al., 2013), and here we focus attention on S defined as the difference in the log10 gpELISA titer at Week 6 minus the same variable at baseline. The biomarker S was measured following a prospective case-cohort sampling design (Prentice, 1986), measured from a 10% random sample of subjects selected at study entry (and with Yτ = 0 and an available Week 6 sample) and from all subjects who experienced the disease endpoint Y = 1 after week 6 (n=1218 vaccine, n=1273 placebo). Figure 1A displays boxplots of S for the vaccine and placebo groups with Yτ = 0, showing higher levels in the vaccine group.
Figure 1.
For vaccine and placebo recipients in the immunological sub-study of ZEST (chosen as a 10% simple random sample, n=1218 vaccine and n=1273 placebo), the (A) boxplots depict the distribution of S|Yτ = 0, the log10 fold-rise of gpELISA antibody titers from baseline (Day 1; pre-immunization) to week 6. Data points are shown for random samples of 100 participants. (B) shows the association between S|Yτ = 0 and baseline gpELISA antibody titers (the BIP) in the vaccine group.
We conduct the analysis assuming Case CB such that P(S(0) = 0|Yτ(0) = 0) = 1. While there is some scatter of S about zero in the Z = 0 placebo group (Figure 1A), we interpret this scatter to be due to measurement error. A testable implication of Case CB is that H0 : E[S(0)|Yτ(0) = 0] = 0 must hold, and the data are consistent with this null hypothesis, with a paired t-test yielding p = 0.71. Under Case CB, the additive-difference CEP surface parameter simplifies to CEP(s1) ≡ CEP(s1,0) = risk1(s1,0) – risk0(s1,0).
EECR is plausible and ENHM highly plausible, with 5 of 11,184 vaccine recipients and 8 of 11,212 placebo recipients experiencing the primary endpoint by τ = 6 weeks. If EECR is violated, the results are unlikely to be sensitive to the assumption deviation, given the small number of early events compared to those occurring after week 6 (25 and 91 events in the vaccine and placebo groups).
We applied the Weibull-model estimated-likelihood method of Gabriel and Gilbert (2014) to estimate CEP(s1), which assumes EECR and accommodates the case-cohort sampling design under a missing at random assumption. This method also accommodates the right-censoring of T that occurred due to drop-out or to end-of-follow-up censoring, under a random censoring assumption. The proportional hazards version of the model was used, given that, based on a coefficient-based Wald test, a parametrized shape component was deemed unnecessary (p=0.78). This Weibull method uses the aforementioned BIP technique (Follmann, 2006; Gilbert and Hudgens, 2008), with the BIP, X, being the baseline/pre-immunization value of the log10 gpELISA titer. The BIP was reasonably well-correlated with S (Figure 1B, Spearman rank correlation −0.58), which improves the accuracy and precision for estimating CEP(s1).
We maximized the estimated likelihood using a parametric normal model for S(1) conditional on X, where model diagnostics supported that the normal model provided a reasonable approximation. Figure 2 shows the estimated CEP(s1) curve for Y = I[T ≤ τ1] for τ1 fixed at 2 years. The estimated CEP(0) is 0.000079 with bootstrap 95% confidence interval −0.0045 to 0.0040, which is consistent with ACN. The estimated curve shows CEP(s1) widely varying and monotone decreasing in S(1), with p-value < 0.001 for variation of CEP(s1) in s1. In addition, the estimated curve is consistent with 1-sided strong ACS, given that it is negative for all values of s1 > 0.016 and the 95% bootstrap confidence intervals for CEP(s1) are below 0 for all s1 > 0.25. Therefore, this principal stratification analysis supports ACN and 1-sided strong ACS. In addition, we applied the weighted pseudo-score method of Huang, Gilbert, and Wolfson (2013) to the ZEST data, which also accommodates the case-cohort sampling design. This method avoids parametric assumptions about the joint distribution of S(1) and X by employing nonparametric estimation of the distribution of S(1) conditional on X and the indicator that S(1) was sampled, with X discretized into quartiles. This analysis also supported ACN and 1-sided strong ACS. Applying Result 1, Sensitivity and Specificity hold, supporting that the fold-rise in gpELISA titer satisfies the Prentice definition of a surrogate endpoint as well as being a useful principal surrogate. In addition, sufficient conditions for a consistent surrogate discussed in Section 4 are met (ACN + 1-sided ACS + EECR + Case CB), supporting that the biomarker is a consistent surrogate. Moreover, both Case CB and EECR may be slightly violated, and Result 4 provides assurance that the inference about the Prentice definition is not sensitive to these minor violations.
We note that, as described in Huang and Gilbert (2011) and Huang, Gilbert, and Wolfson (2013), the employed statistical methods account for the case-cohort sampling design nested within a randomized trial in order to obtain unbiased estimators of CEP(s1); this is why the results of Section 3 hold under a sub-sampling design and the missing at random assumption. If a naive statistical method that ignored the sub-sampling design were used then the estimators of CEP(s1) would be biased and consequently the results would no longer be correct, highlighting the necessity of properly accounting for the sub-sampling design in checking of ACN and ACS.
Figure 2 also highlights the interpretability of the CEP curve analysis, for example allowing researchers to infer that a fold-rise in gpELISA antibody titers from baseline of 10-fold (titer difference = 1.0) corresponds to an estimated clinical efficacy of −0.033; under the no-harm monotonicity assumption, this can be interpreted as 3.3 of 100 vaccine recipients with S(1) = 1.0 avoid zoster disease who would have experienced it had they not been assigned to receive vaccine. Such results are highly interpretable for vaccine researchers and public health policy decision-makers.
Several articles have discussed the limitation of the BIP-based methods for estimating the CEP surface that the modeling assumptions for risk0(s1,s0) are not fully testable (e.g., Gilbert and Hudgens, 2008; Zigler and Belin, 2012). This is a major reason why the BIP + closeout placebo vaccination design has been advocated (Follmann, 2006; Gilbert et al., 2011; Huang, Gilbert, and Wolfson, 2013), as closeout placebo vaccination makes the modeling assumptions for risk0(s1,s0) fully testable. Hence in a very large study, ACN + 1-sided ACS can be fully empirically verified in a BIP + closeout placebo vaccination design under EECR, SUTVA, ignorable treatment assignment, missing at random sampling of S, and random censoring. For applications like the ZEST where a BIP is available but closeout placebo vaccination was not performed, an appropriate causal analysis would include a sensitivity analysis that assesses how the inference depends on violations to any untestable modeling assumptions asserted for risk0(s1,s0). Development of such methods is the subject of current research.
6 Discussion
We studied implications of the principal surrogate criteria ACN and 1-sided strong ACS for the Prentice definition of a valid surrogate endpoint (i.e., Specificity and Sensitivity), and vice versa. We found that in general (for a general S, not in Case CB, and not assuming EECR or EHHM), these two types of criteria do not imply one other. We also found that Case CB together with EECR or ENHM do allow several implications, in particular EECR + Case CB + ACN imply Sensitivity and conversely EECR + Sensitivity imply ACN. Relaxing EECR to ENHM, however, loses the first implication, while the second implication still holds if Monotonicity is added. Apart from Case CB, the only implication that can be derived is that EECR + ACN imply Specificity if NNMEs or Monotonicity hold, and ENHM + ACN imply Specificity if NNMEs or Monotonicity hold. In the ZEST example EECR, Case CB, ACN, and 1-sided strong ACS are consistent with the observed data, illustrating how principal surrogate criteria can be used to help validate the Prentice definition. In addition, we found that Case CB for a binary candidate surrogate S allows more implications. In fact, in the special case EECR + Case CB, ACN + 1-sided strong ACS hold if and only if the Prentice definition holds.
The following question arises– if the principal surrogate criteria are only useful for checking the Prentice definition in Case CB, of what value are the results? Previous authors (e.g., Chan et al., 2012 and Wolfson and Gilbert, 2010) have noted that the Prentice (1989) criteria cannot be checked in Case CB, because there is no variability of the biomarker in the placebo group. However, this article ignores the Prentice (1989) criteria and goes straight to checking the Prentice definition, showing that in Case CB the principal surrogate criteria can be used to check part or all of the Prentice definition. This is useful in practice given that the Prentice definition of the treatment effect on the surrogate being concordant with the treatment effect on the clinical endpoint is a relevant property of a useful surrogate, allowing reliable predictions of clinical efficacy in the same setting of the trial based on the surrogate and guaranteeing a consistent surrogate. Additional research is needed for evaluating the reliability of biomarker endpoints for making inferences about clinical efficacy of new treatments in the same or similar setting (the bridging or transportability surrogate problem), in particular for studying whether and how the principal surrogate/strong effect modifier and/or Prentice surrogate frameworks are useful for this problem.
Acknowledgements
Research reported in this publication was supported by the National Institute Of Allergy And Infectious Diseases of the National Institutes of Health under Award Number R37AI054165. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
7 Appendix: Proofs of Results
We prove the results using 1-sided Specificity and 1-sided Sensitivity; the proofs are similar using 2-sided Specificity and 2-sided Sensitivity.
Proof of Result 1
Examining equation (1)–(4), it follows immediately that ACN implies line (1) equals zero, and EECR implies lines (3) and (4) are zero. Therefore under EECR + ACN
| (5) |
In general, S(1) =d S(0) does not imply CE = 0 (i.e., Sensitivity is not implied), because S(1) =d S(0) is only weakly informative about the joint distribution P(s1,s0). However, in Case CB, (5) simplifies to
| (6) |
In addition, Case CB implies P(S(1) = 0|Y1τ = 0) = P(S(0) = 0|Y0τ = 0) = 1, such that P(0,0) = 1 and P(s1,0) = 0 for all s1 > 0. As a consequence, from (6), CE = 0, such that EECR + ACN + Case CB imply Sensitivity.
Conversely, in Case CB
| (7) |
Now, Sensitivity means that S(1) =d S(0) implies CE= 0, and means that the second term in (7) is zero, such that CEP(0,0)P(0,0)P*(0,0) = 0. Thus ACN holds.
Next, we consider the conditions under which ACN + 1-sided strong ACS imply Specificity. By 1-sided strong ACS, CEP(s1,s0) < 0 for all s1 > s0 with P(s1,s0) > 0. Adding ACN, from (5) it follows that under any of (i) NNMEs, (ii) Monotonicity, or (iii) Case CB, the second term
| (8) |
is bounded above by zero. Therefore, under any of (i), (ii), or (iii), CE < 0, such that Specificity holds. If none of (i)–(iii) hold, however, then ACN + 1-sided strong ACS do not imply Specificity, because the second term (8) may be positive, such that CE in (5) is not necessarily zero (nor is it necessarily negative). Next, suppose Specificity and Sensitivity and all the assumptions (i)–(iii) hold. Because Sensitivity + Case CB imply ACN,
Now, under Case CB S(1) ≠d S(0) implies P(s1,0) > 0 for at least one s1 > 0. Under Specificity, this implies CE ≠ 0, and adding Monotonicity it implies CE < 0. Nevertheless, 1-sided ACS still may not hold for any C ≥ 0, because CEP(s1,0) could be negative for some s1 with P(s1,0) > 0 and nonnegative for other s1 with P(s1,0) > 0.
Proof of Result 2
Under ENHM, line (3) is zero, and under ACN, line (1) is zero. Therefore, under ENHM + ACN
The condition S(1) =d S(0) places only a limited restriction on P(s1,s0) and P*(0,1), such that under all of the extra conditions PEM, NNMEs, Monotonicity, and Case CB, CE still may be non-zero. In fact, under Case CB (with or without NNMEs and/or Monotonicity), S(1) =d S(0) implies CE = CE*(0,1)P*(0,1), which may be nonzero under ENHM. Thus ENHM + ACN + Case CB do not imply Sensitivity.
Conversely, assume Sensitivity, Monotonicity, and Case CB. In Case CB
Now, Sensitivity means that S(1) =d S(0) implies CE= 0, and from the proof of Result 1, P(s1,0) = 0 for all s1 > 0, such that 0 = CE = CEP(0,0)P(0,0)P*(0,0) + CE(0,1)P*(0,1). Now, because CE(0,1) = P(Y(1) = 1|Yτ(1) = 0,Yτ(0) = 1) – 1, CE(0,1) must be non-positive. This implies that CEP(0,0) must be non-negative if P(0,0) > 0. However, by Monotonicity, CEP(0,0) ≤ 0. These results together imply CEP(0,0) = 0 if P(0,0) > 0. Thus ACN holds.
Next, we determine the conditions under which ACN + 1-sided strong ACS imply Specificity. As in the proof of Result 1, adding any of NNMEs, Monotonicity, or Case CB to ENHM + ACN, we obtain
By 1-sided strong ACS, CEP(s1,s0) < 0 for all s1 > s0 with P(s1,s0) > 0. We need to show that S(1) >st S(0) implies CE above is less than zero. If CE(0,1) = 0, then this holds using the same argument as in Result 1. Thus we may assume CE(0,1) ≠ 0, and, because CE(0,1) ≤ 0, we may assume CE(0,1) < 0. This can only make CE smaller, thus CE < 0 and the result follows.
Conversely, Sensitivity + Specificity together with NNMEs, Monotonicity, and Case CB do not imply 1-sided ACS for any C ≥ 0. The proof is the same as for Result 1.
Proof of Result 3
Result 2 shows that under ENHM, ACN does not imply Sensitivity even under the four extra assumptions. Thus with ENHM relaxed, ACN also does not imply Sensitivity. Conversely, assume Sensitivity, Monotonicity, and Case CB. In Case CB
Now, as in the Proof of Result 2, by Sensitivity 0 = CE = CEP(0,0)P(0,0)P*(0,0)+CE(1,0)P*(1,0) + CE(0,1)P*(0,1). Now, by PEM, CE(1,0)P*(1,0) +CE(0,1)P*(0,1) must be non-positive. This implies that CEP(0,0) must be nonnegative if P(0,0) > 0. However, by Monotonicity, CEP(0,0) ≤ 0. These results together imply CEP(0,0) = 0 if P(0,0) > 0. Thus ACN holds.
Next, we consider conditions under which ACN + 1-sided strong ACS imply Specificity. Adding any of NNMEs, Monotonicity, or Case CB to ENHM + ACN, we obtain
By 1-sided strong ACS, CEP(s1,s0) < 0 for all s1 > s0 with P(s1,s0) > 0. We need to show that S(1) >st S(0) implies CE above is less than zero. In general, CE(1,0) can be greater than zero while the remaining terms can be less than zero, and they could exactly counter-balance one another. However, if PEM is added, then CE(1,0) ≤ 0, implying that CE < 0, such that Specificity holds.
Proof of Result 1-Binary
Under EECR and Case CB,
| (9) |
The condition S(1) =d S(0) implies P(0,0) = 1; thus CE = CEP (0,0)P*(0,0). Sensitivity entails that CE = CEP(0,0)P*(0,0) implies CE = 0, implying that CEP(0,0) = 0, i.e., ACN holds.
Next, we also assume Specificity. Specificity (accounting for the fact that ACN holds) states that S(1) >st S(0) implies CE = CEP(1,0)P(1,0)P*(0,0) < 0, which implies both CEP(1,0) < 0 and P(1,0) > 0. From this it follows that if CEP(1,0) ≥ 0, then 1-Sided Specificity could not hold; this contradiction establishes 1-sided strong ACS.
Proof of Result 4
With Pε(s1,s0) defined the same as for P(s1,s0) with constraints under Case CB-ε, the overall clinical efficacy CE under EECR can be written as
| (10) |
| (11) |
Under Case-CB-ε and S(1) =d S(0), Pε(s1,s0) → 0 as ε → 0 for all (s1,s0) ≠ (0,0) and Pε(0,0) → 1 as ε → 0. Examining the above formula for CEε, these convergence results imply that CEε → CEP(0,0) as ε → 0. Therefore Sensitivity implies ACN-ε(0,0). However, ACN-ε does not hold, because CEP(s1,s1) for s1 > 0 is not constrained.
Next we show that EECR + ACN-ε + Case CB-ε imply Sensitivity-ε. Under ACN-ε + Case CB-ε, CEε equals expression (11). By Case CB-ε, when S(1) =d S(0), every Pε(s1,s0) in this expression converges to 0 as ε → 0, showing that CEε → 0 as ε → 0.
Next we note that EECR + ACN-ε + 1-sided strong ACS + Case CB-ε imply Specificity-ε. As above CEε equals expression (11), and under Case CB-ε and S(1) >st S(0), ∑s1<s0 CEP(s1,s0)Pε(s1,s0)P* (0,0) → 0 as ε → 0. By 1-sided strong ACS ∑s1>s0 CEP(s1,s0)Pε(s1,s0)P*(0,0) → ∑s1>0CEP(s1,0)P*(0,0) < 0.
Lastly, the same results attain with EECR replaced with EECR-ε, because CEε now has an extra term stemming from (3) and (4), , which converges to zero as ε → 0.
References
- Chan I, Shu L, Matthews H, Chan C, Vessey R, Sadoff J, Heyse J. Use of statistical models for evaluating antibody response as a correlate of protection against varicella. Statistics in Medicine. 2002;21:3411–3430. doi: 10.1002/sim.1268. [DOI] [PubMed] [Google Scholar]
- Chen H, Geng Z, Jia J. Criteria for surrogate end points. Journal of the Royal Statistical Society, Series B. 2007;69:919–932. [Google Scholar]
- Fleming T, DeMets D. Surrogate endpoints in clinical trials: Are we being misled? Annals of Internal Medicine. 1996;125:605–613. doi: 10.7326/0003-4819-125-7-199610010-00011. [DOI] [PubMed] [Google Scholar]
- Follmann D. Augmented designs to assess immune response in vaccine trials. Biometrics. 2006;62:1161–1169. doi: 10.1111/j.1541-0420.2006.00569.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frangakis C, Rubin D. Principal stratification in causal inference. Biometrics. 2002;58:21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel E, Gilbert P. Evaluating principle surrogate endpoints with time-to-event data accounting for time-varying treatment efficacy. Biostatistics. 2014;15:251–265. doi: 10.1093/biostatistics/kxt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gail M, Pfeiffer R, Van Houwelingen H, Carroll R. On meta-analytic assessment of surrogate outcomes. Biostatistics. 2000;1:231–246. doi: 10.1093/biostatistics/1.3.231. [DOI] [PubMed] [Google Scholar]
- Gilbert P, Grove D, Gabriel E, Huang Y, Gray G, Hammer S, Buchbinder S, Kublin J, Corey L, Self S. A sequential Phase 2b trial sesign for evaluating vaccine efficacy and immune correlates for multiple HIV vaccine regimens. Statistical Communications in Infectious Diseases. 2011a;3(1) doi: 10.2202/1948-4690.1037. Article 4, pMCID: PMC3502884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P, Hudgens M. Evaluating candidate principal surrogate endpoints. Biometrics. 2008;64:1146–1154. doi: 10.1111/j.1541-0420.2008.01014.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P, Hudgens M, Wolfson J. Pearl Judea., editor. Commentary on “Principal stratification– a goal or a tool? The International Journal of Biostatistics. 2011b;7 doi: 10.2202/1557-4679.1341. Article 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y, Gilbert P. Comparing biomarkers as principal surrogate endpoints. Biometrics. 2011;67:1442–1451. doi: 10.1111/j.1541-0420.2011.01603.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y, Gilbert P, Janes H. Assessing treatment-selection markers using a potential outcomes framework. Biometrics. 2012;68:687–696. doi: 10.1111/j.1541-0420.2011.01722.x. pMCID: PMC3417090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y, Gilbert P, Wolfson J. Design and estimation for evaluating principal surrogate markers in vaccine trials. Biometrics. 2013;69:301–309. doi: 10.1111/biom.12014. pMCID: PMC3713795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joffe M. Principal stratification and attribution prohibition: Good ideas taken too far. The International Journal of Biostatistics. 2011;8 doi: 10.2202/1557-4679.1367. Article 12, pMCID: PMC3204670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joffe M, Greene T. Related causal frameworks for surrogate outcomes. Biometrics. 2009;65:530–538. doi: 10.1111/j.1541-0420.2008.01106.x. [DOI] [PubMed] [Google Scholar]
- Ju C, Geng Z. Criteria for surrogate end points based on causal distributions. Journal of the Royal Statistical Society Series B. 2010;72:129–142. [Google Scholar]
- Li Y, Taylor J, Elliott M. A Bayesian approach to surrogacy assessment using principal stratification in clinical trials. Biometrics. 2010;66:523–531. doi: 10.1111/j.1541-0420.2009.01303.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long D, Hudgens M. Sharpening bounds on principal effects with covariates. Biometrics. 2013;69:812–819. doi: 10.1111/biom.12103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao C, Li X, Gilbert P, Chan I. Risk Assessment and Evaluation of Predictions. Springer; New York: 2013. A multiple imputation approach for surrogate marker evaluation in the principal stratification causal inference framework. [Google Scholar]
- Pearl J, Bareinboim E. Proceedings of the Twenty-Fifth National Conference on Artificial Intelligence. Menlo Park, CA: 2011. Transportability of causal and statistical relations: A formal approach. pp. 247–254. [Google Scholar]
- Prentice R. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73:1–11. [Google Scholar]
- Prentice R. Surrogate endpoints in clinical trials: definition and operational criteria. Statistics in Medicine. 1989;8:431–440. doi: 10.1002/sim.4780080407. [DOI] [PubMed] [Google Scholar]
- Schmader KE, Levin MJ, Gnann JW, McNeil SA, Vesikari T, Betts RF, Keay S, Stek JE, Bundick ND, Su S-C, et al. Efficacy, safety, and tolerability of herpes zoster vaccine in persons aged 50–59 years. Clinical Infectious Diseases. 2012;54:922–928. doi: 10.1093/cid/cir970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J, Wang Y, Thibaut R. Counterfactual links to the proportion of treatment effect explained by a surrogate marker. Biometrics. 2005;61:1102–1111. doi: 10.1111/j.1541-0420.2005.00380.x. [DOI] [PubMed] [Google Scholar]
- VanderWeele T. Principal stratification– uses and limitations. The International Journal of Biostatistics. 2011;7 doi: 10.2202/1557-4679.1329. Article 28, pMCID: PMC3154088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T. Surrogate measures and consistent surrogates. Biometrics. 2013;69:561–568. doi: 10.1111/biom.12071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfson J, Gilbert P. Statistical identifiability and the surrogate endpoint problem, with application to vaccine trials. Biometrics. 2010;66:1153–1161. doi: 10.1111/j.1541-0420.2009.01380.x. pMCID: PMC3597127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigler C, Belin T. A Bayesian approach to improved estimation of causal effect predictiveness for a principal surrogate endpoint. Biometrics. 2012;68:922–932. doi: 10.1111/j.1541-0420.2011.01736.x. [DOI] [PMC free article] [PubMed] [Google Scholar]