MATHEMATICAL MODELING OF VENTILATION DEFECTS IN ASTHMA

Abstract

Airway narrowing by smooth muscle constriction is a hallmark of asthma attacks that may cause severe difficulties of breathing. However, the causes of asthma and the underlying mechanisms are not fully understood. Bronchoconstriction within a bronchial tree involves complex interactions among the airways that lead to the emergence of regions of poor ventilation (ventilation defects, VDefs) in the lungs. The emphasis of this review is on mathematical modeling of the mechanisms involved in bronchoconstriction and the emergence of the complex airway behavior that leads to VDefs. Additionally, the review discusses characteristic model behaviors and experimental data to demonstrate advances and limitations of different models.

Introduction

Asthma is a common chronic respiratory disease of the airways that causes difficulty of breathing and may lead in severe cases to death. In 2004, it was estimated that asthma affected about 300 million people worldwide [1], and a recent report for the US showed that its prevalence continues to increase [2]. However, the causes and pathophysiological mechanisms of asthma are not fully understood. Complex behaviors observed in asthma may include interactions among multiple factors such as lung mechanics, the immune system, airway smooth muscle and inflammation [3]. But evidence from imaging and mathematical modeling shows that an integrative model of bronchoconstriction describing airway smooth muscle (ASM), airflow, pressure, and parenchymal tethering of airways within a bronchial tree can explain the complex behavior that emerges during bronchoconstriction causing self-organized heterogeneity of constriction among the airways, and large contiguous regions of poor ventilation (ventilation defects, VDefs) [4].

Bronchoconstriction and ventilation defects

Asthma attacks are triggered by a stimulation of the airway smooth muscle embedded in the bronchial wall. The constriction of the smooth muscle causes narrowing of the airway lumen, which increases airway resistance. Higher airway resistance results in a decrease of the forced expiratory volume during the first second of exhalation (FEV1), which is commonly used for clinical assessments of airway obstruction.

In vitro stimulation of airway smooth muscle in tissue strips [5,6], lung slices [7,8] or isolated airways [9,10] results in smooth muscle constriction. Extrapolation from these results of isolated tissue samples to an in vivo airway tree would suggest that smooth muscle stimulation should result in the constriction of all airways. However, a CT imaging study showed that a fraction of airways paradoxically dilated after stimulation by methacholine or cold-air hyperpnea [11]. Imaging of ventilation during bronchoconstriction using positron emission tomography (PET) [4,12–15], MRI [16–19] or synchrotron CT [20,21] showed large ventilation defects in the lungs that are evidence for major heterogeneity in airway constriction. Also, neither CT nor PET-CT imaging found narrowing of large central airways (> 2mm) sufficient to explain ventilation defects. In fact, a recent PET-CT imaging study combined CT-based segmentation of the large central airways and PET-based measurements of ventilation to estimate peripheral airway (< 2mm) resistance and found a dramatic increase during bronchoconstriction [22].

The apparent contradictions among these findings of airway behavior during bronchoconstriction illustrate that observations from in vitro experiments cannot fully explain the results of in vivo imaging. Airway smooth muscle is obviously an essential element of airway behavior during an asthma attack since bronchoconstriction, increased mucus secretion, and inflammation can contribute to airway lumen narrowing in response to a stimulus [23]. However, the behavior of an isolated airway smooth muscle or a single airway in response to a stimulus alone cannot explain the emergence of heterogeneity in bronchoconstriction and the VDefs observed in imaging studies. Particularly, why does the severe bronchoconstriction that causes VDefs seem to occur in peripheral airways, and why is that severe peripheral constriction clustered in large contiguous regions?

Mathematical modeling

Stimulation of ASM causes a tension that results in shortening unless it is opposed by the load of a counteracting force greater than or equal to the tension generated by the muscle. In airways, ASM is embedded in their walls such that its shortening causes narrowing of their lumen, as it has been observed in vitro in isolated airways [9]. In contrast, intrapulmonary airways are embedded in lung parenchyma so that lung inflation and tissue deformation due to airway narrowing contribute to the load opposing the tension generated by ASM. Thus, ASM shortening is affected by external conditions and not only by the stimulation of the ASM and its contractile properties.

Lai-Fook published in 1978 an elegant mathematical model describing the airway radius as a function of these interacting forces at the airway wall [24]. The output parameters of that model depend only on the current input so that the model has no memory of previous states, and is in terms of system theory a static model. From a historical perspective of mathematical modeling that builds on previous generations, this static model of a single airway can be considered the first generation [25]. Interestingly, using a similar static model, Peter Macklem found that low lung inflation pressures or decoupling possibly due to a layer of edema between lung parenchyma and ASM may result in airway instability [26]. In another study, investigators found that differences in parameters of a static model representative for differences between normal and asthmatic airways may result in airway instability [27]. In spite of differences among these static models, they have an essential mechanism in common that is the equilibrium of interacting forces at the airway wall (ASM, parenchymal tethering, transluminal pressure difference) coupled by wall geometry. Thus, airway radius is affected by the tension that the stimulated ASM generates as well as by other factors such as lung inflation, edema at the airway wall, or airway remodeling. In fact, increasing both ASM activation and lung inflation pressure may result either in no change of the equilibrium of forces at the airway wall, constriction, or dilation.

Anafi and Wilson published in 2001 a dynamic model of a single terminal airway that extended Lai-Fook’s static model to include the effect of airway narrowing on the airflow through the airway and, thus, on the transbronchial pressure and the inflation of the surrounding lung parenchyma [28]. The Anafi and Wilson model demonstrated that airways may become unstable and close completely when peak airway entrance pressure falls below a critical value. Reopening of a closed airway required a higher airway entrance pressure, giving rise to a range of pressures with bistable behavior where an airway could be either open or closed. It is important to note that the model of Anafi and Wilson applies a pressure-controlled and sinusoidal input at the airway entrance, and that the solutions obtained are only for steady state conditions.

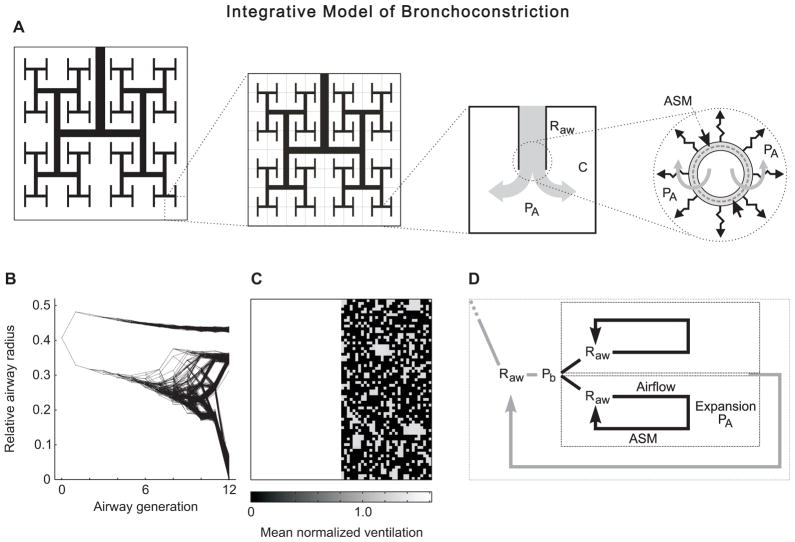
Mathematical modeling of VDefs requires a scope that extends beyond a single airway in order to explain the spatial patterns of VDefs that involve many airways. However, in order to explain how local mechanisms contributing to bronchoconstriction may cause complex airway behaviors, the model needs to integrate mechanisms and interactions ranging from single airways and ASM to the whole organ. Such an integrative model of bronchoconstriction was first described in 2005, and included a bronchial tree with 12 generations of airway branching and the mechanisms of the Anafi and Wilson model for each individual airway of that tree [4] (Fig. 1A). This means that individual airway radii changed according to the local forces acting at the airway wall. However, a change in radius of a single airway affected the distribution of airflow, pressure, and parenchymal expansion during breathing throughout the rest of the airway tree. These changes affected the constriction of other airways while the airway itself was affected by changes in other airways. Thus, the individual airways respond to their local conditions, but their interconnection with other airways and the lung parenchyma results in interdependent airway behavior.

Figure 1.

Schematic overview of the integrative model of bronchoconstriction and the behavior of the computational model. A: The model includes an airway tree with 12 generations of airway bifurcations. All terminal units include a compliance (C) so that airflow changes the volume and the alveolar pressure (P_A). The local forces acting on the wall of each individual airway of the tree determine airway radius and, thus, its resistance (R_aw). The local forces include airway smooth muscle (ASM), parenchymal tethering, and the transmural pressure difference. B: The relative radius of all airways of the airway tree during bronchoconstriction is dependent on the airway generation and exhibits a very high heterogeneity that emerges at a critical point when airways become unstable and a feedback mechanism leads to a differentiation among the interdependent airways. C: Map of normalized ventilation of the terminal units of the model. The location of the terminal units on the map corresponds to the schematic tree in A that is similar to a Mandelbrot tree. D: Schematic of the feedback loop that causes airway instability. The pressure at a bifurcation (P_b) is the entrance pressure for both daughter airways and their subtending regions. The airway resistance (R_aw) affects the airflow through the airway, the peak expansion during the breathing cycle, and airway narrowing due to an interaction with the ASM. Since airway radius determines R_aw, a positive feedback may result in either further constriction or dilation, and propagate to neighboring airways during the self-organized clustering of bronchoconstriction and the emergence of VDefs. The model includes feedback loops for all airways so that they are hierarchically organized.

In that computational model, progressive ASM stimulation resulted in increasing airway constriction up to a critical point where a catastrophic shift in bronchoconstriction (Fig. 1B) resulted in the emergence of VDefs (Fig. 1C) [4] (reference includes an animation of that process in supplemental video S6). Neither static nor dynamic models of single airways could explain the emergence of VDefs during bronchoconstriction since they cannot describe spatial patterns. Even if a dynamic model of a single airway is used for each terminal airway of a bronchial tree with 12 generations, the coupling of airflows and pressures throughout the bronchial tree does not result in a clustering of bronchoconstriction and an emergence of VDefs, but rather in a scattered closure of terminal units [4].

The emergence of VDefs is caused by interdependence among airways interconnected within a bronchial tree, and a feedback loop that has been described in detail [29]. Briefly, when increasing bronchoconstriction reaches a critical point where airways become unstable then any small perturbation reducing airflow in one daughter airway of a bifurcation leads to a smaller tidal volume and, thus, lower peak expansion of the lung parenchyma surrounding that airway (Fig. 1D). Less expansion increases airway narrowing and causes an increase in airway resistance, further decreasing airflow through its lumen compared to other parallel pathways. This triggers a vicious cycle, also referred to as positive feedback, that further increases the constriction of that airway. If the global tidal volume does not change then any decrease in local tidal volume in some terminal units must be balanced by an increase in other terminal units increasing their expansion and dilating the affected airways. However, interdependence among airways within a bronchial tree includes coupling due to pressure, airflow, and parenchymal expansion (Fig. 1A and 1D). For any airway, the parenchymal expansion affecting its radius is linked to the local tidal volume flowing through its lumen and, thus, to the average relative expansion of its subtending terminal units (Fig. 1D). Increased constriction of an airway may propagate to proximal neighbors if it decreases local tidal volume and parenchymal expansion of the parent airway. Distal propagation is a result of decreasing local tidal volume and parenchymal expansion of subtending units. Proximal and distal propagation of constriction result in self-organized clustering of bronchoconstriction and the emergence of VDefs (Fig. 1B and 1C).

The Anafi and Wilson model suggested that airway behavior may be bistable so that there should be only two well-separated modes of airway radii: moderate and severe constriction. However, the distribution of airway radii found in a bronchoconstricted tree of the integrative model showed a wider spectrum with more than two modes (Fig. 1B) [30]. What causes these differences? The models are driven by different input conditions: pressure-controlled vs. volume-controlled. The results of the Anafi and Wilson model were based on pressure-controlled conditions at the entrance of a single terminal airway [28]. In contrast, VDefs emerged in the integrative model of bronchoconstriction under conditions with controlled tidal volume at the airway entrance [4]. That is a major difference because under volume-controlled conditions an increase in the overall airway resistance during bronchoconstriction results in increased pressure amplitudes at the entrance of the airway tree. However, at each bifurcation of the airway tree the two daughter airways and their subtending branches of the tree have the same pressure as input. Thus, local pressures affect the airflow distribution within the airway tree while the sum of airflows is linked to volume control at the organ level. For pressure-controlled conditions at the entrance of an airway tree [31], airways exhibited a behavior that was different from that of the dynamic model of a single airway, showing the effect of airway interdependence within the bronchial tree. Also, it should be noted that pressure-controlled conditions at the terminal airway entrance of the Anafi and Wilson model are not equivalent to the same conditions at the entrance of an airway tree. For example, a decrease in airflow due to terminal airway constriction may decrease the pressure drop from the tree entrance to the terminal airway entrance so that the entrance pressure of the terminal airway increases. Such interactions may explain the stability of airways at a section of the S-shaped airway radius vs. entrance pressure relationship that is inaccessible with constant pressure amplitudes at the airway entrance.

Emergent behavior

The term “multi-scale model” has been frequently used in recent years, and is often linked to criticism of reductionist approaches although the criticism is in most cases inaccurate. Models that include relatively small entities as elements linked to a much larger structure such as a whole organ are often described as multi-scale models, so that the term characterizes the length-scale range of mechanisms and interactions included in the model. However, the modeled details within that range are unclear and may cause errors. For example, extrapolations from single airway behavior to whole organ behavior may be sufficient for specific conditions, but fail for others if the global behavior is not fully explained by the smaller entity. In contrast, network models including nonlinear properties may exhibit emergent behaviors that originate from complex interactions among their elements, but that are different from the behaviors of their elements [32], as the integrative model of bronchoconstriction described above demonstrates. Philip Anderson argued in 1972 in an excellent essay about emergent behavior published in Science that “the reductionist hypothesis does not by any means imply a constructionist one” [33]; the ability to identify behaviors of the elements of a system does not mean that it is possible to construct from that knowledge the behavior of the whole system. The integrative model of bronchoconstriction can serve as an example to illustrate that argument; mathematical modeling of single airway behavior is an essential reductionist approach for an understanding of bronchoconstriction, but it does not allow one to construct whole organ behavior. VDefs emerge as a new behavior from interactions among the elements of the hierarchical network of an airway tree. In general, studies of phenomena that emerge from complicated interactions within a large network rely critically on mathematical and computational modeling, since the number of interactions within large networks makes it virtually impossible to derive analytical solutions for overall network behavior, or to dissect the network experimentally. The emergence of complex behavior in such models means that the constructionist hypothesis failed, but not the reductionist approach.

Physiological and clinical insights

Mathematical modeling of the emergence of VDefs aims at understanding the complex behavior of airways during asthma attacks. There are also approaches that combine data from different modalities such as imaging, three-dimensional computational modeling, and oscillatory ventilation mechanics to identify distributions of the degree and location of airway constriction that could be consistent with both imaging and mechanical data [22,34]. Other investigators have developed a multi-scale approach that links sub-models with scopes at different length and time scales to cover the overall range from molecular to organ level [35], but these approaches are beyond the scope of this review.

From a clinical perspective, understanding the mechanisms leading to VDefs may enhance patient care. For example, treatment of asthma patients with inhaled therapies works well when symptoms are mild, but as bronchoconstriction worsens, patients often require oral or intravenous delivery of medication to relieve the symptoms. This behavior is expected from the integrative model of bronchoconstriction, where delivering anti-inflammatory or bronchodilating medication to areas that are already well ventilated may lead to spatial heterogeneity in drug delivery and worsening of VDef formation in areas that are poorly ventilated. Therefore, delivery of medication through inhalation prior to the emergence of VDefs or breathing maneuvers that reduce VDefs prior to the inhalation could be expected to improve treatment outcomes and limit side effects of therapy. Alternatively, developing strategies to deliver inhaled therapies to poorly ventilating regions could also be expected to improve treatment outcomes. In mechanical ventilation, pressure-controlled modes may be associated with a higher risk in case a minor change triggers a positive feedback with decreasing tidal volume, but compared to classical volume-controlled modes pressure-control may be better able to resolve of VDefs [22]. The mechanistic understanding that the integrative model of bronchoconstriction provides could also lead to better monitoring of patients with asthma. Ventilation heterogeneity (with formation of VDefs) shifts the critical point favoring airway closures and, thus, could be used as a target for clinical monitoring. Indeed, a recent clinical study [36] showed that monitoring ventilation heterogeneity with multi-breath nitrogen washout performed better than spirometry or exhaled nitric oxide as a marker of asthma control. In addition to multi-breath nitrogen washout, forced oscillatory mechanics or functional imaging with PET or MRI are also techniques that could be used to measure ventilation heterogeneity.

Beyond modeling of VDefs in asthma, similar phenomena may be seen in other pulmonary conditions, such as the acute respiratory distress syndrome. In this condition, impaired surfactant and flooding of the lungs with edematous fluid may cause a bistability in airway patency that may involve interactions similar to the integrative model of bronchoconstriction. However, it remains to be seen whether the formation of regions of atelectasis from impaired surfactant behaves in a similar way to the formation of VDefs.

The integrative model of bronchoconstriction was developed to explain the emergence of VDefs observed in our imaging studies. However, there are a number of experimental observations by other investigator that the model may explain. Some of these observations were even characterized as paradoxical, and were not thought to be linked to each other before the mechanistic link by the integrative model was recognized [30,37]. Such agreement between predicted behaviors and experimental data for a number of very different phenomena suggests that the model may include a set of mechanisms that may be fundamental for bronchoconstriction in general.

Conclusions

Mathematical modeling has yielded an integrative model of bronchoconstriction that could explain the emergence of ventilation defects and the associated heterogeneity of bronchoconstriction. Also, evidence suggests that the mechanisms included in the model may be relevant for a wider range of phenomena related to bronchoconstriction in the lungs. Understanding mechanisms involved in bronchoconstriction, aided by the model, may help to guide the development of novel therapeutic approaches.