Significance
To the best of our knowledge, our data provide the first imaging evidence compatible with columnar processing of sound frequency in the human auditory cortex. Our study depicts the human auditory cortex with unprecedented spatial detail and demonstrates the feasibility of acquiring submillimeter functional images outside visual/motor cortices, setting the stage for a wide range of research possibilities. Our results elucidate the role of cortical layers in bottom-up and top-down processing of sounds, and suggest that ongoing behavioral goals shape population-based sound representations especially in superficial layers of A1 columns. These results may inform and improve computational models of auditory cortical processing and may be relevant for understanding neurological conditions that do not yet have an imaging “biomarker” (e.g., tinnitus).
Keywords: columns, tonotopy, fMRI, 7-Tesla, depth-dependent
Abstract
Columnar arrangements of neurons with similar preference have been suggested as the fundamental processing units of the cerebral cortex. Within these columnar arrangements, feed-forward information enters at middle cortical layers whereas feedback information arrives at superficial and deep layers. This interplay of feed-forward and feedback processing is at the core of perception and behavior. Here we provide in vivo evidence consistent with a columnar organization of the processing of sound frequency in the human auditory cortex. We measure submillimeter functional responses to sound frequency sweeps at high magnetic fields (7 tesla) and show that frequency preference is stable through cortical depth in primary auditory cortex. Furthermore, we demonstrate that—in this highly columnar cortex—task demands sharpen the frequency tuning in superficial cortical layers more than in middle or deep layers. These findings are pivotal to understanding mechanisms of neural information processing and flow during the active perception of sounds.
Auditory perception starts in our ears, where hair cells at different places in the cochlea respond to different sound frequencies. The spatially ordered arrangement of neural responses to frequencies (tonotopy) that arises from this transduction mechanism is preserved in subcortical (1, 2) and cortical stages of processing, where neuronal populations form multiple tonotopic maps (3, 4). At the cortical level, tonotopic maps describe systematic changes along the surface. In the orthogonal direction (i.e., perpendicular to the cortical surface), aggregates of neurons with parallel axons have been reported (5, 6). These anatomical observations of cortical microcolumns inspired invasive electrophysiological investigations in cats (7), demonstrating that frequency preference is constant across cortical depth (i.e., frequency columns). Since this early study, frequency columns have been observed in a variety of animals (3, 8–10), and a columnar organization has been suggested for other acoustic properties (10, 11). Despite this anatomical and physiological evidence from animal models, the role of cortical columns in auditory perception is not understood (6, 12, 13). To unravel intracolumnar computations, it is of fundamental importance to analyze the transformation of information across cortical depths. Differences in cell types and in patterns of input and output projections suggest a distinct role of cortical layers in neural information processing (5). In particular, behavioral demands and ongoing brain states can modulate the functional properties of layer 2/3 neurons, suggesting that supragranular neuronal populations may be of fundamental relevance for the processing of sensory information in a context-dependent manner (14). Recordings in the primary auditory cortex of animals have shown differences across layers in response latency (15, 16), in frequency selectivity (i.e., tuning width) (8, 16), and in the complexity of neuronal preference to acoustic information (i.e., receptive field) (17). However, the reports are not concordant across species. Moreover, most of the knowledge regarding auditory columnar processing has been obtained in anesthetized animals, making its relation to human behavior unclear.
To date, there is no functional evidence for a columnar organization and for the layer-dependent processing of sound frequency in the human auditory cortex from either invasive or noninvasive recordings. In this study, we address this question noninvasively using high magnetic field (7 tesla) functional magnetic resonance imaging (fMRI) at high spatial resolution and specificity (18, 19). We acquired functional images in the primary auditory cortex (PAC) of five healthy volunteers and estimated the best frequency (BF) responses voxel-by-voxel. Then, by analyzing the 3D spatial variations of these responses, we identified the PAC regions with a stable arrangement of BF across cortical depths. The term “column” has been used with multiple meanings in the past (13). Here, we refer to columnar region as the cortical region where the variation of frequency with depth is significantly smaller compared with the frequency variation orthogonal to depth (i.e., across the surface) (SI Text). Further, we examined the functional differences across cortical layers by estimating the cortical depth-dependent changes in frequency tuning during an auditory and a control visual task. We hypothesized that additional top-down processing engaged by the auditory task would modulate the frequency tuning of fMRI responses in the PAC in a cortical depth-dependent manner. Finally, we simulated how the observed changes of frequency tuning across layers and tasks may result in behaviorally relevant changes of neuronal population-based sound representations.
Results
Initial Identification of the Primary Auditory Cortex and High-Resolution Cortical Sampling.
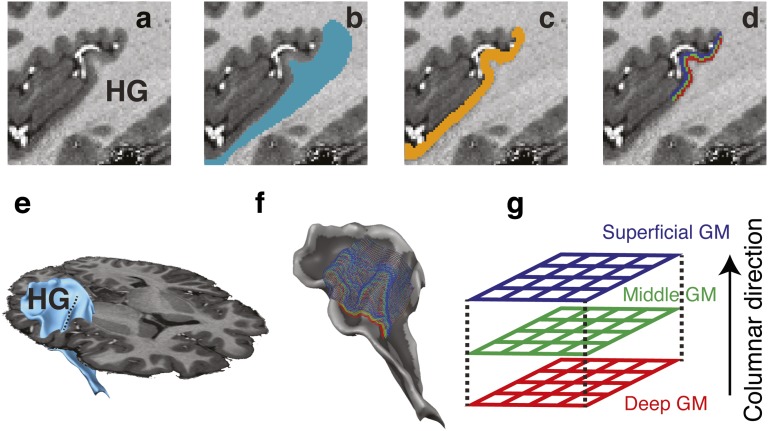
Each volunteer underwent two scanning sessions. In the first session, we acquired a tonotopic functional localizer with a magnetic resonance (MR) acquisition weighted by the effective transversal relaxation time (T2*-weighted) covering the entire auditory cortex (SI Text). Data from these measurements were used to obtain large-scale tonotopic maps and to identify the most likely location of the PAC in each individual. This information was used for positioning the higher resolution functional measurements in the second session. Furthermore, in the first scanning session, we collected high-resolution (0.6 mm isotropic) anatomical data [weighted by: longitudinal relaxation time (T1-weighted; T1w); proton density (PD-weighted; PDw); and the effective transversal relaxation time (T2*-weighted; T2*w) (in three of the five subjects)]. The combination of T1w and PDw images resulted in unbiased anatomical images with a good contrast between white matter and gray matter (20). These images were used to obtain a precise definition of the gray matter cortical ribbon (Fig. 1 A–C) and to derive a 3D surface grid (Fig. 1D) enabling the sampling of an fMRI signal at the white/gray matter boundary (Fig. 1E) and at different relative cortical depths (Fig. 1F and SI Text). Points at different cortical depths on the grid follow the direction of maximal cortical thickness variation (Fig. 1G). We refer to this direction as the “columnar direction” of the grid. This process was limited to the PAC region as localized by the large-scale tonotopic responses and the high-resolution myelin-related contrast (when available) that was obtained combining T1w and T2*w images (21). This procedure resulted in the segmentation of the most medial two thirds of the Heschl’s gyrus (HG), in agreement with previous human postmortem anatomical studies of the human PAC (22). In agreement with previous literature (23), we estimated the average cortical thickness of this region of interest to be 2.7 mm (SE across participants = 0.06 mm).
Fig. 1.
Illustration of the anatomical segmentation procedure. Anatomical images (A) are segmented to identify the white matter (B) and gray matter (C) in the region of interest [Heschl’s gyrus (HG)]. The white/gray matter boundary is used to reconstruct 3D surfaces [blue in E; with cortical curvature (light gray, gyrus; dark gray, sulcus) in F]. The gray matter region is used to estimate the cortical thickness and obtain regularly spaced grids (n = 3; red, green, and blue in D, F, and G) used to evaluate the distribution of functional responses orthogonally to the white/gray matter boundary (i.e., columnar direction).
Analysis of Tonotopic Responses Averaged Across Cortical Depths.
In the second session, we acquired high-resolution (0.8 mm isotropic) functional images weighted by the transversal relaxation time (T2-weighted). The high specificity of the T2-weighted measurements came at the cost of a limited field of view (SI Text). In fact, for all our participants, the functional data of the second session were limited to a portion of the right auditory cortex, which was defined, subject-by-subject, based on the data acquired in the first session (SI Text). During the measurements, participants listened to frequency sweeps (1,000 ms long, upwards and downward, each spanning a frequency range of 0.4 octaves, exponential change of frequency over time) centered at six frequencies (0.2–6.4 kHz) while fixating on a centrally displayed cross. Per stimulation block, sweeps with one center frequency were presented (eight sweeps per block with an intertrial interval of 1 s). Additionally, within a block, the center frequency of sweeps varied ±0.1 octaves around the block’s center frequency. As a result, sweeps across blocks did not overlap in their frequency content. Both upward and downward sweeps were presented. The fixation cross, which was white during silence, changed to either blue or red together with sound presentation. During each run, participants were asked to perform a visual or an auditory task (six blocks per task). In the visual task, subjects had to indicate the color change (blue vs. red) of the fixation cross. In the auditory task, subjects had to indicate the direction of the sweep (up vs. down). In gerbils, learning to categorize up and downward sweeps has been previously shown to induce changes in the neuronal representations at the level of PAC neurons (24), and we hypothesized that our task would also induce measurable effects at the level of neuronal populations in the human PAC.
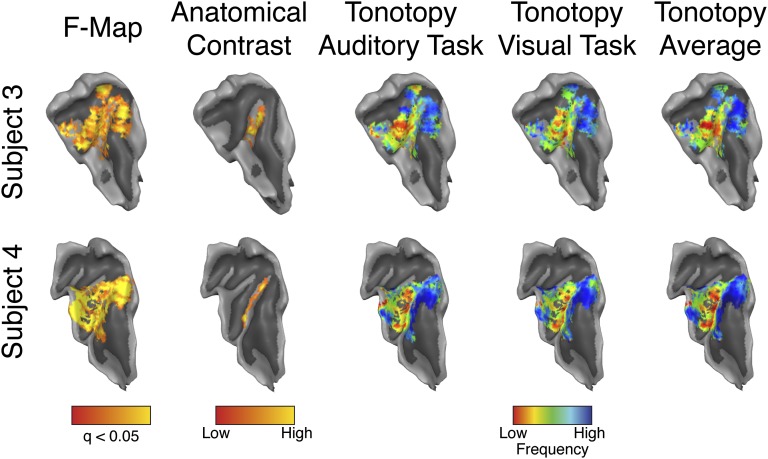
The functional data were analyzed to estimate the responses to all conditions (six frequencies for each of the two tasks) using a standard general linear model. For a first quality assessment, the data were averaged across depths and projected on the surface boundary between white matter and gray matter. In all subjects, the sounds elicited significant [using a threshold (q) corrected for multiple comparisons using false discovery rate; q(FDR) of <0.05] responses in the right medial two thirds of HG and the adjacent Heschl’s sulcus (HS). Furthermore, responses were present in the portions of planum temporale and polare that were included in the acquisition field of view (Fig. 2 and Fig. S1). The voxels’ BF was determined as the frequency eliciting the strongest response (4) for the two tasks separately. When examining the spatial layout of BF (averaged across cortical depths) (Fig. 2 and Fig. S1), all subjects showed a mirror-reversed topographical organization of frequency preference (tonotopy) for both tasks. Specifically, a region of low frequency preference was present on HG. Regions preferring higher frequencies were located posteromedially and anterolaterally to HG (4).
Fig. 2.
Single-subject (subject 3 and subject 4) results. The overall response to the sounds (F-Map; FDR corrected q < 0.05), intracortical anatomical contrast related to myelin (T1/T2*), and tonotopic maps (auditory task, visual task, and average) are projected on the individual surface reconstruction of the right temporal cortex. For all other subjects, see Fig. S1.
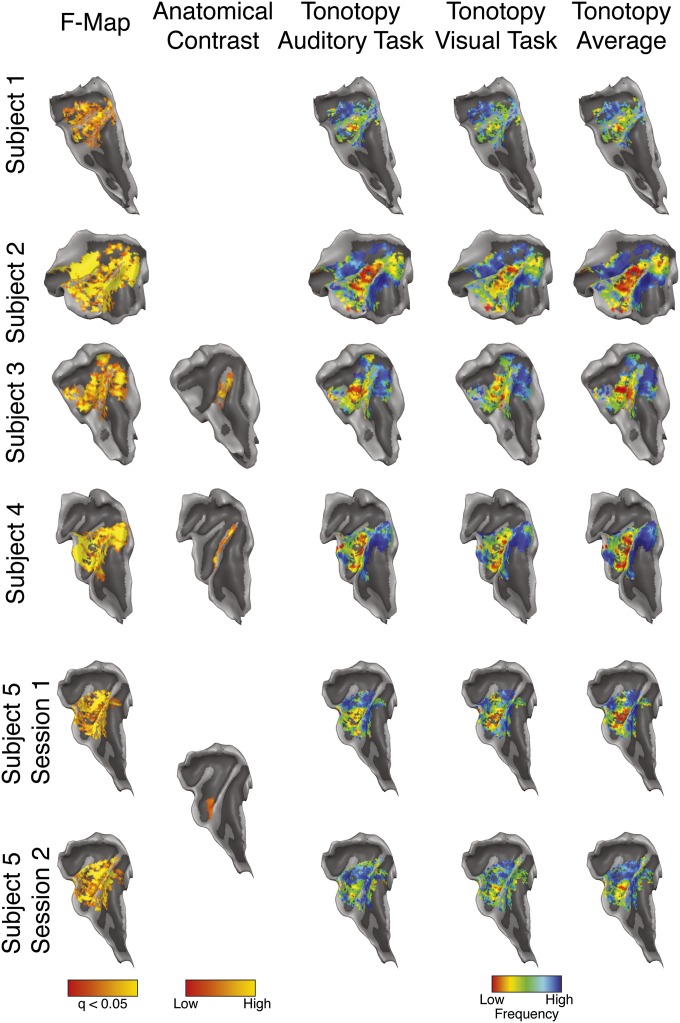
Fig. S1.
Single-subject results. The overall response to the sounds (F-Map; FDR corrected q < 0.05), intracortical anatomical contrast related to myelin (T1/T2*), and tonotopic maps (auditory task, visual task, and average) are projected on the individual surface reconstruction of the right temporal cortex.
Mapping of the Cortical Depth-Dependent Organization for Frequency Processing.
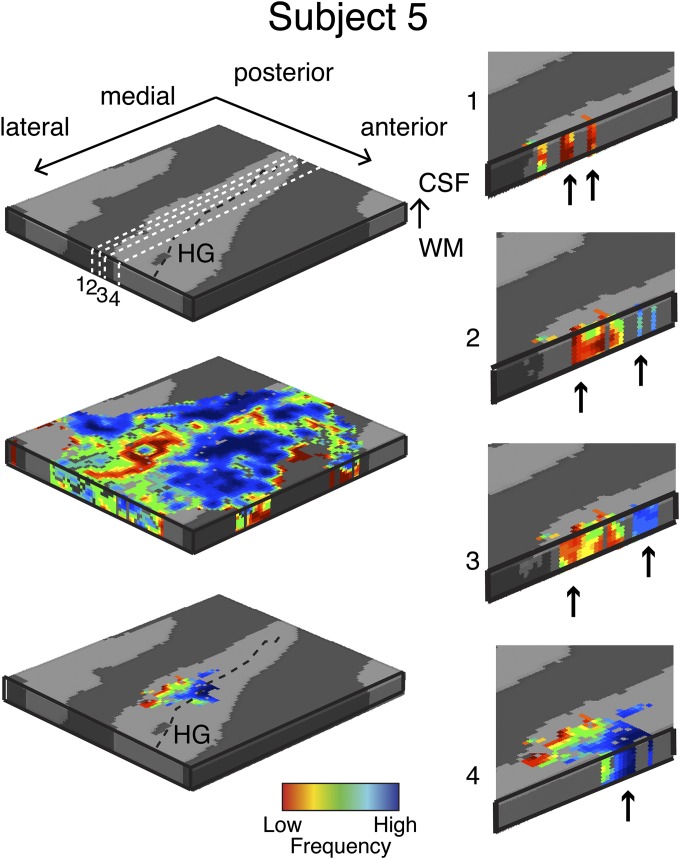
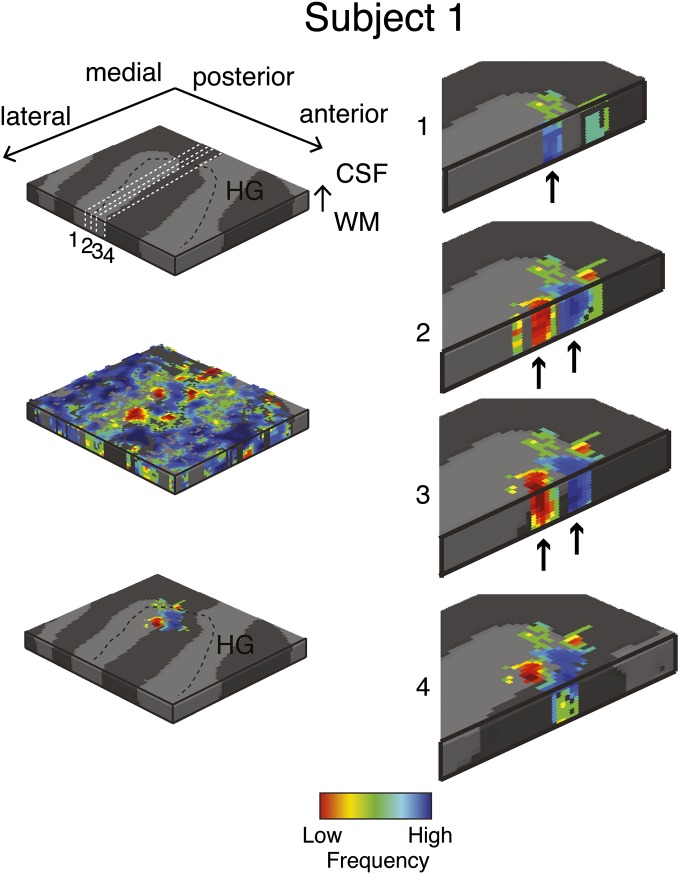
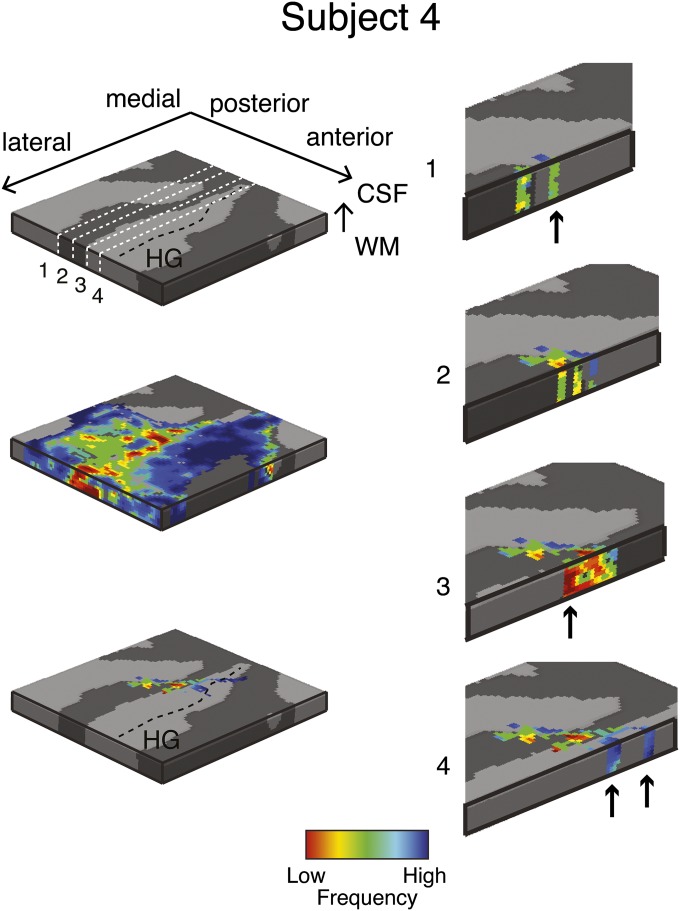
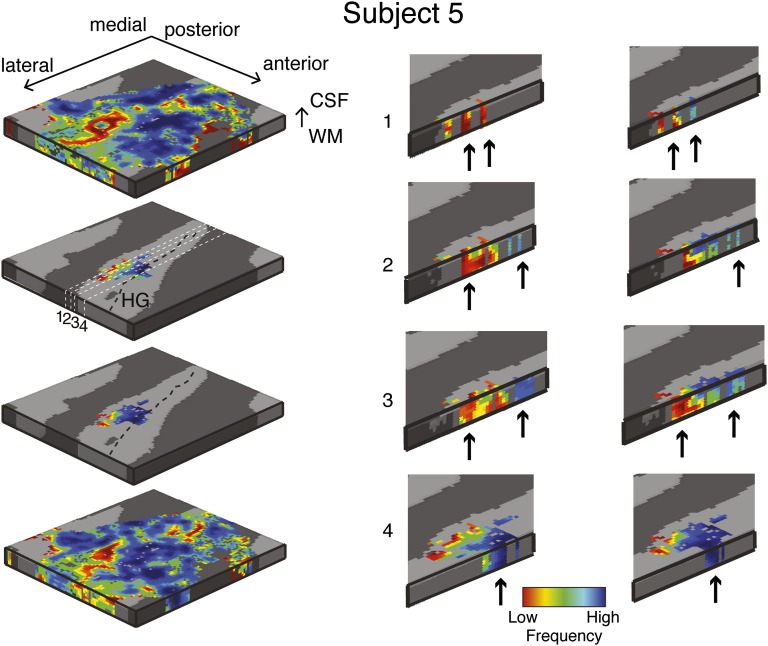
After this initial analysis, we investigated whether frequency preference was constant across cortical depths. We sampled the single voxel functional responses to sounds of all six center frequencies in the depth-dependent grid space, independently for the two tasks. For each task, this analysis resulted in frequency response profiles for each grid point in the range (0.2–6.4 kHz). Per task, we estimated each grid point’s BF (the frequency eliciting the strongest response) and, using a fitting procedure (SI Text), the full width at half maximum (FWHM) of the frequency response for that grid point. We obtained an estimate of tuning width (TW) as the ratio between the grid point’s BF and the FWHM. The tonotopic maps at different cortical depths were submitted to an analysis that evaluated the gradient of frequency change in three dimensions. From the tonotopic gradient, we obtained a measure of “columnarity” as the ratio between the components of the gradient parallel and orthogonal to the columnar direction (SI Text). The ratio R was distributed in the interval (0.0004–1.8) for each individual subject. Across subjects, the average median value of R was 0.2 (SE = 0.02). Values greater than R = 1 indicate regions where the tonotopic map varied more along the cortical surface than across cortical depths (the columnar direction). Note that this procedure may underestimate columnarity in regions that present a stable frequency preference within spatially extended patches on the cortical surface. In each subject, we tested for significance of the frequency columnarity ratio with permutation testing (SI Text). The analysis was repeated for both tasks, and the regions that, after permutation testing, resulted in a significant (P < 0.05 uncorrected) columnarity ratio in at least one of the tasks were selected. We refer to these regions as frequency columns. The average significant threshold of R across our participants was 0.49 (SE = 0.0045). We found such regions in the most medial portion of HG in all subjects (Fig. 3 and Figs. S2–S5). We demonstrated the reliability of these regions by comparing measurements taken several days apart (Fig. S6) and addressing potential confounds of the acquisition (Fig. S7). At lower cortical depths, the columnar region in HG was characterized by high intracortical contrast related to myelin (measured in vivo in three subjects) (Fig. S8), a characteristic of the primary auditory cortex (21, 22).
Fig. 3.
Single-subject columnar analysis. Tonotopic maps are computed in the grid space of the right HG. Permutation testing is used to determine grid locations with a significant (P < 0.05) columnar tonotopic arrangement (Bottom Left). (Right) Mediolateral cuts through HG and displays the vertical distribution of frequency preference in the columnar region. Arrows indicate example locations with high similarity in BF across cortical depths within the columnar region. For all other subjects, see Figs. S2–S6 and Movies S1–S6.
Fig. S2.
Single-subject (subject 1) columnar analysis. Tonotopic maps were computed in the grid space of the right Heschl’s gyrus (HG, see Top Left for anatomical information). Permutation testing was used to determine grid locations with significant (P < 0.05) columnar tonotopic arrangement (Bottom Left). To highlight the vertical distribution of frequency preference, the columnar region is presented through four cuts in the medial-to-lateral direction of the grid space (Right). Arrows indicate example locations with high similarity in best frequency across cortical depths within the columnar region.
Fig. S5.
Single-subject (subject 4) columnar analysis. Tonotopic maps were computed in the grid space of the right Heschl’s gyrus (HG) (see Top Left for anatomical information). Permutation testing was used to determine grid locations with significant (P < 0.05) columnar tonotopic arrangement (Bottom Left). To highlight the vertical distribution of frequency preference, the columnar region is presented through four cuts in the medial-to-lateral direction of the grid space (Right). Arrows indicate example locations with high similarity in best frequency across cortical depths within the columnar region.
Fig. S6.
Single-subject (subject 5) reproducibility of columnar analysis. Tonotopic maps of two separate sessions (Top Left and Bottom Left) were computed in the grid space of the right HG. Permutation testing was used to determine grid locations with a significant (P < 0.05) columnar tonotopic arrangement (two Middle Left panels). To highlight the vertical distribution of frequency preference, the columnar region is presented through four cuts in the medial-to-lateral direction of the grid space (session 1, Middle column; session 2, Right column). Arrows indicate example locations with high similarity in best frequency across cortical depths within the columnar region.
Fig. S7.
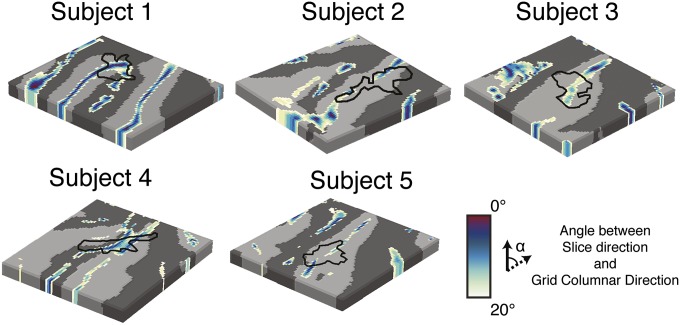
Comparison of columnar region and slice acquisition direction. The angle (α) between the slice acquisition direction and the columnar direction of the grid is mapped for every single subject. The region with significant columnar tonotopic organization is outlined in black. The columnar region does not correspond fully to regions that are characterized by a small angle with respect to the direction of the slices in the acquisition. This result indicates that our results cannot be explained by the potential acquisition-induced blurring in this direction.
Fig. S8.
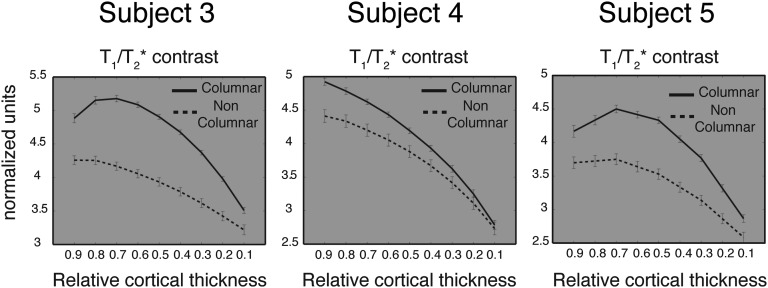
Depth-dependent (deep gray matter – relative cortical thickness = 0.9); superficial gray matter – relative cortical thickness = 0.1) anatomical contrast (T1/T2*) in the columnar region (full line) and noncolumnar regions (dashed line). Note that the columnar region exhibits stronger anatomical contrast (i.e., more myelin-related signal) in the deep cortex, a characteristic of primary-like sensory areas. This result demonstrates that the columnar region is situated in the primary auditory cortex.
Fig. S3.
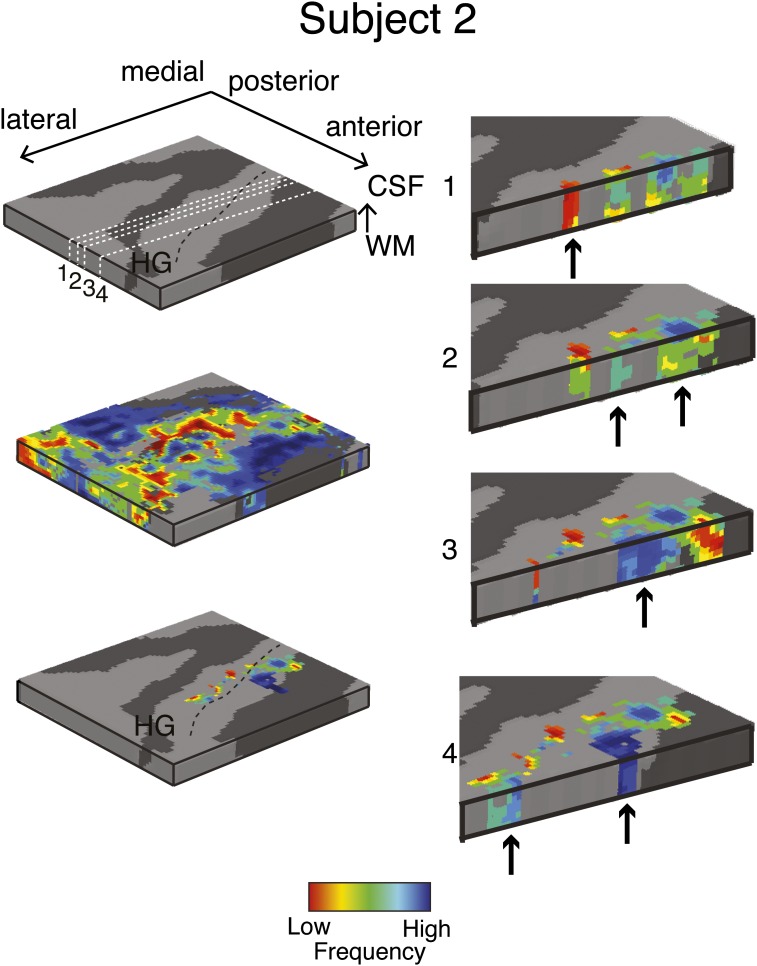
Single-subject (subject 2) columnar analysis. Tonotopic maps were computed in the grid space of the right Heschl’s gyrus (HG, see Top Left for anatomical information). Permutation testing was used to determine grid locations with significant (P < 0.05) columnar tonotopic arrangement (Bottom Left). To highlight the vertical distribution of frequency preference, the columnar region is presented through four cuts in the medial-to-lateral direction of the grid space (Right). Arrows indicate example locations with high similarity in best frequency across cortical depths within the columnar region.
Fig. S4.
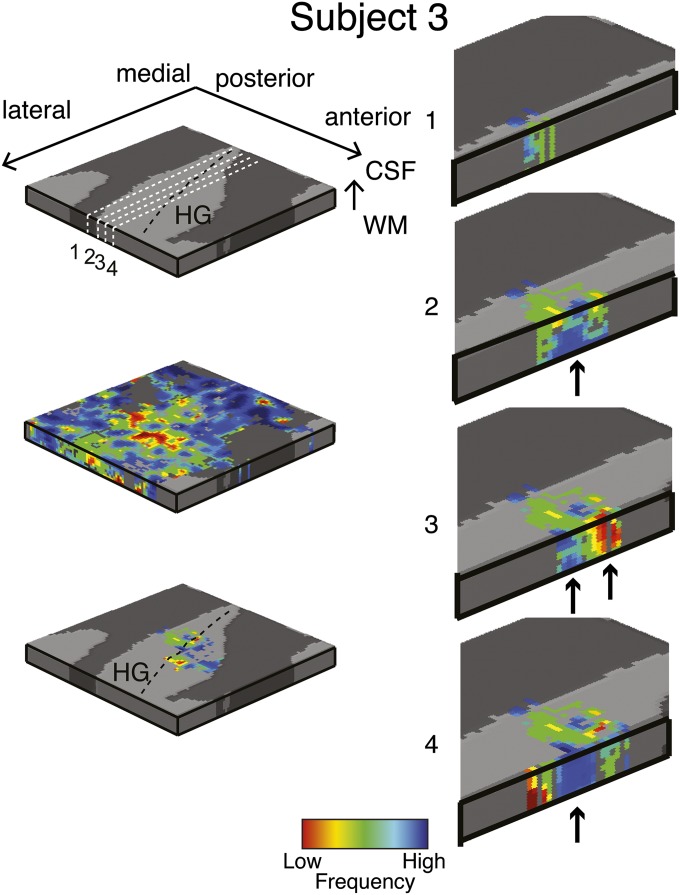
Single-subject (subject 3) columnar analysis. Tonotopic maps were computed in the grid space of the right Heschl’s gyrus (HG) (see Top Left for anatomical information). Permutation testing was used to determine grid locations with significant (P < 0.05) columnar tonotopic arrangement (Bottom Left). To highlight the vertical distribution of frequency preference, the columnar region is presented through four cuts in the medial-to-lateral direction of the grid space (Right). Arrows indicate example locations with high similarity in best frequency across cortical depths within the columnar region.
To quantify the cortical distribution of frequency in highly columnar regions of the PAC, we calculated on each participant’s cortical surface the iso-frequency contours corresponding to the maximum frequency and to the frequencies one to four octaves lower. We then measured the cortical area covered by responses spanning one octave (i.e., we calculated the surface area within iso-frequency lines). Averaging across octave intervals and subjects, we obtained an estimate of 16 mm2 (±3 mm2, SE), per octave.
Task- and Layer-Dependent Modulations of Frequency Tuning.
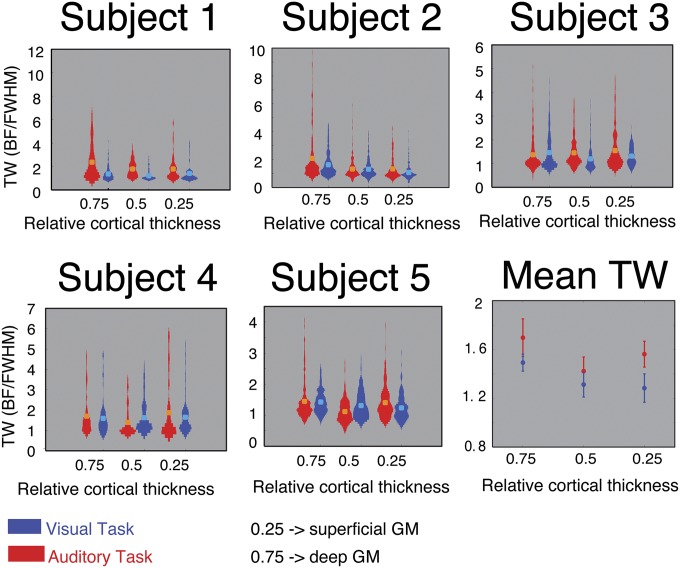
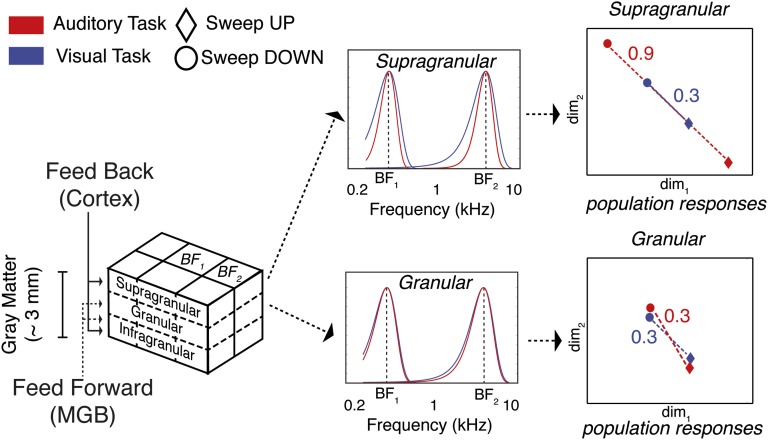
Within the identified columnarly organized HG regions, we did not observe significant changes in the overall fMRI response with task. This result is possibly due to the relative simplicity of both tasks: Behavioral performance was of 91% and 92% for the auditory and visual tasks, respectively, with no significant difference across tasks and subjects. Furthermore, frequency preference did not show any significant change across the two tasks. Instead, we observed a narrower tuning width during the auditory task compared with the visual task (Fig. 4). At the group level, the difference was significant (P < 0.05, paired t test) at superficial cortical depths only. This finding suggests that a selective refinement of acoustic information occurs within a column and that top-down information relevant to behavior acts primarily in superficial layers and to a lesser degree in deeper layers. In fact, in our experiment, narrower frequency tuning allowed better discrimination at the neuronal population level between upward and downward sweeps. A simulation of tonotopic responses with BF and TW in the ranges obtained with our fMRI responses illustrates this effect (Fig. 5, Right and SI Text).
Fig. 4.
Task-dependent modulation of tuning width across cortical depths. Single-subject distributions are presented together with subjects’ mean TW value (orange and cyan dots). The mean across subjects (Bottom Right) is presented together with error bars indicating the SE across subjects. At superficial cortical depths (0.25 relative cortical thickness), TW values were significantly higher for the auditory task compared with the visual task, indicating narrower tuning (P < 0.05; paired t test).
Fig. 5.
Effect of frequency tuning width sharpening on the population responses to upward and downward sweeps. The pattern of cortical depth-dependent inputs to a columnar region of primary auditory cortex (5, 40) is summarized on the Left. For two different cortical depths (i.e., supragranular and granular), the frequency response of different units is simulated as a Gaussian function with mean equal to the BF and full width at half maximum (FWHM = BF/TW) equal to the value empirically estimated from our fMRI data. The task modulation (red, auditory task; blue, visual task) acts on the TW: i.e., sharpens the frequency response in the supragranular but not in the granular layer. Average responses to upward and downward sweeps (circles and diamonds, respectively) are represented using 2D multidimensional scaling. As a result of the sharpening, the Euclidean distance between upward and downward sweeps during the auditory task increases at the population level in the supragranular layers.
Discussion
Our results provide direct evidence of a stable arrangement of frequency preference across depths of the human primary auditory cortex (Fig. 5, Left). We analyzed the gradients of frequency preference on the cortical surface and across cortical depth in the right HG and adjacent HS in five healthy volunteers. By doing, so we did not identify single discrete columnar entities, but rather showed that the most medial portion of HG exhibited significantly smaller variability of the population frequency preference in the direction orthogonal to the cortical surface compared with the rest of the imaged field of view. We refer to this region as a highly columnar region of the cortex. The identification of the columnar region in single subjects was remarkably stable across tasks even at several days of separation. Further, the columnar locations exhibited higher cortical contrast related to myelin in deep sections of the cortex, a characteristic of the PAC (22). To achieve high spatial specificity and resolution, our functional (T2-weighted) scans were acquired with field of view restriction and covered one hemisphere.
The presence of regions with almost constant frequency preference across cortical depth reflects the relevance of frequency processing in these cortical regions, but by itself it does not reveal the nature of the computations that are performed within these regions. To investigate the nature of these computations, we analyzed cortical depth-dependent changes induced by different tasks. Previous literature has shown that fMRI can detect layer-dependent signal changes using both T2*-weighted and T2-weighted measurements (25–30). We analyzed the differential changes induced by the auditory and visual tasks on the frequency population tuning and selectivity. We were able to show that population level frequency responses sharpen with cortical depth when attending to the auditory stimuli. These results provide strong evidence that acoustic information processing in primary cortical areas is modulated by task demands, a result that has been debated in the literature (31–34). Further, we demonstrate that attention can selectively improve neural processing of acoustic information within a column by sharpening the receptive field in upper cortical (supragranular) layers (Fig. 5, Center). At the neuronal population level, this effect results in increased distance between the responses to upward and downward sweeps (Fig. 5, Right). The sharpening of the tuning width may be explained by the task-induced phase reset of frequency-selective neuronal populations, which has been shown to have the most pronounced effects in supragranular auditory layers (35, 36).
Previous animal studies have shown that the shape of receptive fields of primary auditory neurons can be modulated by a detection (37) and discrimination (38) task compared with passive listening. Here, by asking participants to perform either a visual or auditory task, we were able to modulate population frequency responses and observe these changes noninvasively with fMRI. These changes were visible despite the relatively weak manipulation of attention (task performance was 91% and 92% for the auditory and visual task, respectively). The effective relation and relevance to behavior of this mechanism need to be further investigated: e.g., by manipulating parametrically the difficulty of an auditory task.
Our study of frequency preference paves the way for in vivo investigations into the fine-grained representation and processing of acoustic properties in auditory cortex. Using complex stimuli, such as dynamic ripples and natural sounds, it is possible to derive the neuronal population preference to spectrotemporal acoustic properties beyond frequency (39). Together with those stimuli, the methods used here can be exploited to investigate cortical depth stability or laminar variability of neuronal population tuning to other acoustic features, such as spectral and temporal modulations, aural dominance and binaural interaction, and frequency sweep direction (10, 11, 16). Finally, this study provides the basis for investigating neuronal population receptive field changes during increasingly complex auditory and multisensory tasks. Specifically, future studies of auditory feature detection, discrimination, and learning will enable the generalization of the top-down mechanism we uncovered here.
Materials and Methods
Five subjects (median age = 25 y, all females) participated in the study. The subjects had no history of hearing disorder or neurological disease. The Institutional Review Board (IRB) for human subject research at the University of Minnesota granted approval for the study, and procedures followed the principles expressed in the Declaration of Helsinki. Informed consent was obtained from each participant before conducting the experiments.
In a first session, we measured high-resolution (0.6 × 0.6 × 0.6 mm3) anatomical images, allowing a precise definition of the gray matter cortical ribbon (20) and the functional activation elicited by amplitude-modulated tones (n = 5; with voxel size = 1.5 × 1.5 × 1.5 mm3) (SI Text). These measurements covered the entire right hemisphere of each subject, and the large-scale tonotopic maps obtained from the analysis of these data were used to localize the primary auditory cortex (PAC) individually. Additionally, in three subjects, this information was complemented by the acquisition of high-resolution (0.6 × 0.6 × 0.6 mm3) anatomical data whose contrast is related to the myelin content, enabling an anatomical localization of the PAC (21).
Using this individually tailored localization information, in a second session, we zoomed into the functional responses of individuals’ right PAC by acquiring high spatial resolution (nominal voxel size = 0.8 × 0.8 × 0.8 mm3) T2-weighted functional data. Sounds were blocked with respect to center frequency and were presented in silent gaps between the acquisitions of functional volumes to reduce contamination with the scanner noise. All data analysis was performed at the individual subject level. To evaluate the reproducibility of our results, we asked one of the participants (subject 5) to perform the full experiment a second time at several days distance and repeated the analysis independently for the two datasets.
SI Text
SI Materials and Methods
Subjects.
Five subjects (median age = 25 y, all females) participated in the study. Subject 5 participated twice in the study to assess the reproducibility of the results.
Auditory Stimuli.
In the main experiment, stimuli consisted of 1,000-ms-long frequency sweeps (upward and downward; spanning 0.4 octaves; sampling rate 16 kHz) centered at six different central frequencies (0.2, 0.4, 0.8, 1.6, 3.2, and 6.4 kHz). For each center frequency, we also created sweeps with a center frequency ±0.1 octave. For example, for the first center frequency (0.2 kHz), additional sweeps with a center frequency at 0.187 kHz (0.2 kHz – 0.1 octave) and 0.214 kHz (0.2 kHz + 0.1 octave) were created. Because sounds were presented in blocks, this small variation in the sounds’ center frequency was implemented to minimize neuronal adaptation and subject disinterest. All stimuli were created in MATLAB (Mathworks Inc.). During the fMRI scanning, subjects were asked to attend either the direction (up vs. down) of the sweep (auditory task) or the color (red vs. blue) of the fixation cross that changed concomitant with sound presentation (visual task) and respond using an MR compatible button box (two alternative forced choice).
Because the MRI acquisition sequence used for the main experiment covered only a limited portion of the brain (see Functional and Anatomical MRI Measures), we identified the most likely location of the primary auditory cortex (PAC) in individuals before commencement of the main experiment (session 2). That is, in a separate session (session 1), we acquired functional data in response to a tonotopic localizer. In this localizer, the stimuli consisted of sounds grouped into eight conditions (three tones and five semantic category conditions). We analyzed only the responses to the tones. Amplitude-modulated tones were created in MATLAB (8 Hz, modulation depth of 1) with a carrier frequency of 0.45, 0.5, and 0.55 kHz for the low-frequency condition; 1.35, 1.5, and 1.65 kHz for the middle frequency condition; and 2.25, 2.5, and 2.75 kHz for the high-frequency conditions. Sounds were sampled at 16 kHz, and their duration was cut to 800 ms.
In both the main study and the localizer, sound onset and offset were ramped with a 10-ms linear slope, and their energy (root mean square) levels were equalized. Inside the scanner, ∼60-dB sounds were presented with an MR compatible audio system designed with piezoelectric elements (linear frequency transfer function up to ∼8 kHz; Sensimetrics). This intensity is necessarily loud because, despite the use of silent gaps in the volume repetition time (TR), the sounds have to compete with the loud scanner noise that happens just before and after the presentation of each sound.
Before starting the measurement, sounds were played to the subject, and the intensity of individual sounds was further adjusted to equalize their perceived loudness.
Overview of the Study.
Each subject participated in two separate scanning sessions (subject 5 repeated session 2 twice for reproducibility purposes). In session 1, we acquired high-resolution anatomical data and low-resolution functional gradient-echo echo planar imaging (GE-EPI) data. These functional GE-EPI data were used solely for defining the region of interest for the acquisitions in session 2. Other than that, they did not enter the analyses reported here. The high-resolution anatomical data were resampled to match the resolution of the functional data of session 2 and were used for segmentation and for the cortical sampling analysis (see below).
In session 2, we acquired low-resolution anatomical data and high-resolution functional gradient- and spin-echo (GRASE) data. These functional GRASE data were acquired within the slabs defined by the functional localization achieved in session 1 and were used in all analyses described below. To align these high-resolution functional data (of session 2) to the high-resolution anatomic data (of session 1), we followed a two-step procedure: First, the low-resolution anatomical data (of session 2) were aligned to the high-resolution anatomical data of session 1. Second, based on this anatomy-to-anatomy alignment, the high-resolution functional GRASE data of session 2 were aligned to the high-resolution anatomical data of session 1. Below, the acquisition parameters and the analysis pipeline are described in detail.
Functional and Anatomical MRI Measures.
In the first scanning session, data were acquired on a 7-T whole-body system driven by a Siemens console operating a whole-body gradient coil. A head coil (1 Tx, 32 Rx channels; NovaMedical Inc.) was used to acquire anatomical [T1-weighted; proton density (PD)-weighted; T2*-weighted] and functional data for spatial localization. Anatomical data (0.6 mm isotropic) were acquired using a modified magnetization prepared rapid gradient echo (MPRAGE) sequence [T1w: repetition time (TR) = 3,100 ms; inversion time (TI) = 1,500 ms (adiabatic nonselective inversion pulse); echo time (TE) = 3.5 ms; flip angle = 5 degrees; generalized autocalibrating partially parallel acquisitions (GRAPPA) factor = 3; field of view (FOV) = 229 × 229 mm; matrix size = 384 × 384; 256 slices; pixel bandwidth = 180 Hz per pixel; first phase encode direction anterior to posterior; second phase encode direction left to right; PD: TR = 2,160 ms; TE = 3.5 ms; flip angle = 5 degrees; GRAPPA factor = 3; FOV = 229 × 229 mm; matrix size = 384 × 384; 256 slices; pixel bandwidth = 180 Hz per pixel; first phase encode direction anterior to posterior; second phase encode direction left to right; T2*w: TR = 4,910 ms; TE = 16 ms; flip angle = 8 degrees; GRAPPA factor = 3; FOV = 229 × 229 mm; matrix size = 384 × 384; 256 slices; pixel bandwidth = 480 Hz per pixel; first phase encode direction anterior to posterior; second phase encode direction left to right]. T2*-weighted functional data (1.5 mm isotropic) were acquired using a clustered GE-EPI technique (i.e., sounds presented in silent gaps within TRs). Sounds were presented grouped in blocks consisting of six sounds (block duration, 18 s). Each block was separated by 12 s of no stimulation. Each condition was presented twice per run, with six runs acquired per subject [44 slices (ascending interleaved order, no gap between slices); matrix size = 128 × 128; FOV = 192 × 192; GRAPPA factor = 3; partial Fourier 6/8; anterior-to-posterior phase encoding direction; pixel bandwidth = 2,441 Hz per pixel; TR = 3,000 ms; time of acquisition (TA) = 1,500 ms; TE = 17 ms].
Data for the main experiment were acquired during a second session, which was conducted on a 7-T whole-body system driven by a Siemens console using a head gradient insert (operating up to 80 mT/m with a slew rate of 333 T⋅m−1⋅s−1). The high performance head gradient insert is advantageous for high-resolution functional imaging, allowing significantly reduced read-out times and decreasing geometric distortions, required acceleration, and voxel blurring. A custom-made surface coil (1 Tx, 24 Rx channels) was used to acquire additional anatomical (T1-weighted; PD-weighted) and high-resolution functional data. Anatomical data (1 mm isotropic) were acquired using a modified MPRAGE sequence [T1w: TR = 2,500 ms; TI = 1,500 ms (adiabatic nonselective inversion pulse); TE = 4.29 ms; flip angle = 4 degrees; GRAPPA factor = 2; FOV = 208 × 256 mm; matrix size = 208 × 256; 176 slices; pixel bandwidth = 140 Hz per pixel; first phase encode direction anterior to posterior; second phase encode direction left to right; PD: TR = 1,670 ms; TE = 4.29 ms; flip angle = 4 degrees; GRAPPA factor = 2; FOV = 208 × 256 mm; matrix size = 208 × 256; 176 slices; pixel bandwidth = 140 Hz per pixel; first phase encode direction anterior to posterior; second phase encode direction left to right]. T2-weighted high-resolution (0.8 mm isotropic) functional images were acquired using 3D-GRASE (41) with inner volume selection (14 slices; matrix size = 32 × 256; FOV = 25 × 206 mm; TE = 28.58; TA = 250 ms; TR = 2,000 ms). Sounds were presented grouped in blocks consisting of eight sounds (block duration, 16 s) with each block separated by 10 s with no stimulation. Each condition (n = 12; six frequencies and two tasks) was presented once per run (∼6 min), and we acquired a minimum of 8 and up to a maximum of 12 runs per subject (depending on the willingness of the subject). We imaged the right hemisphere of each subject due to constraints dictated by the B1 transmit profile of the surface coil. Transmit power was calibrated in each subject to obtain the required flip angles in the auditory cortex.
Although high magnetic fields permit the acquisition of higher spatial resolution images due to the increased signal-to-noise ratio (42, 43) and the increase in blood oxygen level-dependent (BOLD) contrast (44, 45), high spatial resolution alone is not sufficient to achieve higher spatial specificity of the functional responses. The BOLD response is limited by the underlying vascular contributions and their respective spatial point spread functions (43). Conventional T2*-based BOLD contrast, which is used in the vast majority of fMRI studies [gradient-echo echo-planar imaging (GE-EPI)], is sensitive to both micro- and macrovasculature components at high magnetic fields (43, 46–50). As a result, effects from large draining veins (penetrating the cortex orthogonally or lying on top of the gray matter surface) can be pronounced in BOLD signals obtained with GE-EPI (25–29, 46, 47, 50, 51). On the other hand, T2-weighted [spin-echo echo-planar imaging (SE-EPI)] is substantially less sensitive to large vein effects (19, 52) and has been used to map columnar organizations in the visual cortex in vivo (18, 19). Due to limitations in power deposition, nonuniform B1 fields, and reduced overall BOLD contrast (48, 49, 52), previous studies using SE-EPI have been restricted to a single thick slice and small fields of view, hampering the investigation of cortical depth-dependent measurements and sensory areas outside of the visual cortex. As an alternative to conventional SE-EPI, 3D GRASE (gradient and spin echo) (41, 53) has been used to generate T2-weighted functional images over a 3D volume, achieving high isotropic resolutions that allow investigations of columnar (54) and laminar level effects (55) with increased specificity with respect to GE-EPI (30). However, the field of view of 3D GRASE is still limiting field (∼10 mm in the slice direction), and, for this reason, we used data acquired in the first scanning session to localize the main tonotopic gradient in each individual right hemisphere. The acquisition slab of the 3D GRASE data was placed on the high-to-low tonotopic gradient in the medial two-thirds of Heschl’s Gyrus (HG). Although there is debate about the interpretation of tonotopic maps in terms of the underlying auditory fields (56, 57), these interpretations agree that the medial two-thirds of HG cover the PAC.
Anatomical Data Analysis.
The anatomical data analysis was performed using custom MATLAB code and BrainVoyager QX (Brain Innovation). First, datasets with different anatomical contrasts were divided to enhance the desirable features in the respective images. That is, we divided T1w by PDw images (T1w/PDw) to remove signal intensity biases related to transmit-and-receive profiles of the RF coil, while also enhancing the contrast between gray and white matter (20). Similarly, in the three subjects in which we acquired T2*w anatomical data, we divided T1w by T2*w images (T1w/T2*w) to enhance intracortical tissue contrast related to myelin. Finally, the ratio between PDw and T2*w images, while reducing the white/gray matter contrast, enhanced contrast between veins and the brain, permitting robust removal of veins from the analysis. Anatomical images were further corrected for residual inhomogeneities (IIHC) using a multiplicative model with a polynomial of the third order (58). The high-resolution (0.6 mm isotropic) data of session 1 were then sampled at a resolution of 0.8 mm isotropic.
Second, we defined the cortical ribbon based on the T1w/PDw images. That is, for each subject, we manually segmented the white/gray matter border in a region of interest that included HG and adjacent regions in the planum temporale and polare. Next, automatic region-growing tools and additional manual editing were used to delineate the border between gray matter and cerebral-spinal fluid and compute the cortical thickness of the cortical ribbon using the Laplace method (59). The Laplace method is used because it provides a unique reciprocal thickness measurement even in regions where cortical thickness varies across space. Solutions of the Laplace partial differential equation have to fulfill the constraint that the sum of the (unmixed) second partial derivatives of the MR intensity values (with respect to x, y, and z) is zero. This constraint is fulfilled if the gradient slopes do not change along each dimension. The estimation of the Laplacian starts by setting two different arbitrary intensity values, one at the white–gray matter (WM–GM) boundary (e.g., value 100) and one at the gray matter-cerebrospinal fluid (GM–CSF) boundary (e.g., value 200) and setting the mean value (e.g., value 150) to gray matter voxels. A solution of the Laplace equation corresponds to a smooth transition of intensity values from one boundary to the other. Such a solution can be found simply by keeping the values at the cortex boundaries to fixed values (e.g., values 100 and 200) and by iteratively smoothing the intensity values in between (gray matter voxels) until the resulting intensity values no longer change. From the obtained smooth field, a gradient of intensities can be calculated pointing in the direction of cortical depth at each gray matter voxel. Integrating along these gradient values produces “field lines” or “streamlines” (59) to travel from the white/gray matter boundary to the pial surface (or vice versa). These field lines point in the “columnar” depth direction, creating a local coordinate system together with two orthogonal directions along the cortical extent. For straight patches of cortex with a constant thickness, these streamlines correspond to straight lines (orthogonal to the cortical surface) connecting points at the WM/GM boundary with corresponding points at the GM/CSF boundary. For cortex patches with nonconstant thickness, the resulting streamlines are slightly curved, establishing a unique one-to-one mapping between corresponding points at the WM/GM boundary and the GM/CSF boundary.
Third, we constructed a horizontal grid at a fixed relative depth level (0.25, 0.5, and 0.75 of cortical thickness). These grids are equivalent to “equipotential surfaces” (59) and are built by stepping in two orthogonal directions with respect to the streamline gradient, resulting in regularly spaced grid sample points at a given relative depth value. The traversal through gray matter requires x/y/z gradient values at arbitrary 3D coordinates, which is obtained by trilinear interpolation from neighboring voxel values. The emerging grid is constantly fine-tuned to assure that horizontal and vertical distances are kept constant, forming extended regular grids that can be subsequently used to topographically sample aligned functional (and other) datasets. Because of the unique correspondence between grid points at different cortical depths, this method is particularly suited to study possible columnar organizations of functional responses. An additional set of grids at nine cortical depths was computed for visualization purposes only. This procedure is visualized in Fig. 1.
Finally, the anatomical data were used to compute maps of myelin-related contrast. That is, the T1w/T2*w were limited to the cortical ribbon. Large superficial and cortical veins were identified by thresholding an individual’s venograms (i.e., the PDw/T2*w images), and voxels exceeding the defined threshold were removed from the T1w/T2*w images. The resulting maps of myelin-related contrast were linearly rescaled in the (1–10) range (21).
Functional Data Analysis.
Functional data processing was performed using custom MATLAB code and BrainVoyager QX (Brain Innovation). GE-EPI series from session 1 were slice-scan-time–corrected, motion-corrected, high pass-filtered (three cycles per run), temporally smoothed (two neighboring data points), coregistered to the high-resolution anatomical scans acquired in the same session, and resampled in the 3D anatomical space at a resolution of 1.6 mm isotropic. A standard general linear model analysis with eight predictors (three frequencies and five semantic categories) was used to estimate the response in each experimental condition. All further analyses were limited to voxels that responded significantly to the sounds [F-map; q(FDR) < 0.05]. Tonotopic maps (4) were derived by color coding each voxel according to the frequency to which it responded best (i.e., its “preferred” or “best” frequency). These maps were projected on the individual’s reconstruction of the surface boundary between white matter and gray matter of the right temporal lobe, which allowed locating the main tonotopic gradient. The tonotopic gradient [high (posteromedial Heschl’s gyrus) to low frequency (medial HG)] in the medial portion of each subject’s right Heschl’s gyrus was used to locate the most likely position of the primary auditory cortex (57). In three subjects, the location of the tonotopic gradient was complemented by the region with the highest intracortical contrast related to myelin (21).
Preprocessing of the high-resolution functional GRASE data from session 2 included motion correction, high pass filtering (three cycles per run), and temporal smoothing (two neighboring data points). After preprocessing, each functional run was coregistered to the intrasession anatomical scans. Initial alignment was based on information available in the header of the acquisition files. Fine-tuning alignment was performed manually. To aid this process, we enhanced anatomical contrast by averaging the volume across time points. The information obtained from the alignment of the anatomical data obtained in the two sessions was used to create 0.8 mm isotropic functional time series coregistered to the high resolution anatomical scans of session 1.
A standard general linear model analysis with twelve predictors (six frequencies × two tasks) was used to estimate the response to each condition for each subject independently. All further analyses were limited to voxels that showed a significant response to all sounds [F-map; q(FDR) < 0.05]. Tonotopic maps (4) were derived by color coding each voxel according to the frequency to which it responded best. These maps were projected on the individual’s reconstruction of the surface boundary between white matter and gray matter of the right temporal lobe, which allowed locating the main tonotopic gradient in a manner similar to the lower resolution localizer. Fig. S1 shows the overall activation and tonotopic maps (auditory and visual task and their average) for all individual subjects projected on the surface reconstruction of the right HG. Note the similarity between the tonotopic maps elicited by the two tasks. We further validated the reproducibility of the results by performing the same analysis on data of the same individual acquired several days apart (subject 5), which resulted in strikingly similar maps.
Single condition functional responses (percent signal change) were sampled in the grid space to allow the investigation of their columnar arrangement. The vertical direction (z) of the grid space represents the direction locally orthogonal to the cortical surface (i.e., columnar direction). Horizontal directions (x, y) represent the local direction of the plane tangent to the cortical surface. To avoid biases in our analysis due to insufficient sampling, we excluded grid locations (at all cortical depths) characterized by an estimated cortical thickness smaller than 1 mm from all subsequent analysis. For both tasks independently, we analyzed the grid points’ frequency profiles in the range (0.2–6.4 kHz). We defined the best frequency (BF) of every grid point as the condition that elicited the strongest functional response. A Gaussian fit (with its mean constrained to the grid point’s BF) was used to obtain a tuning width (TW) estimate, computed as TW = BF/FWHM (where FWHM = full width at half maximum of the best fitting Gaussian curve). Note that high and low values of TW indicate narrow and broad frequency tuning, respectively. Figs. S2–S5 and Fig. 3 report all single-subject maps rendered in the grid space. The relatively smooth transition from one color to the next denotes the presence of a frequency gradient, and an isofrequency line corresponds to lines where the color remains constant. The data from the two separate sessions of subject 5 (Fig. S6) were used to investigate the reproducibility of these results.
To identify the columnar regions of frequency preference in each task (i.e., during the visual and auditory task), we computed at each grid point the 3D gradient [gx = dfx/dx, gy = dfy/dy gz = dfz/dz; where dfx is the variation of frequency in direction x at grid point i and dx is the cortical space (in mm) over which this variation takes place] of changes in preference throughout the tonotopic maps. The ratio R = (gx2 + gy2)/gz2 results in higher values for smaller changes of best frequency in the columnar direction. Note that this procedure may underestimate columnarity in regions that present a stable frequency preference in the direction orthogonal to the columnar direction (i.e., in regions in which gx and gy are very small). To obtain a single measure over the cortical sheet, the final measure of columnar responses was the local average of R in a neighborhood of 3 × 3 × 3 grid points. As a result, we obtained one 2D map of regions with columnar tonotopic responses. We assessed significance of R as follows. We permuted (NP = 1,000) the tonotopic maps while preserving the 3D smoothness. Next, we performed the columnarity analysis on the permuted maps and thereby obtained an empirical null distribution of the R values. We found in all subjects one cluster in the most medial portion of HG where the columnar measure R was significant (P < 0.05, permutation testing) in both tasks independently. We excluded all voxels outside this region from the remainder of the analysis. Figs. S2–S5 and Fig. 3 report all single-subject tonotopic maps thresholded by the columnarity analysis, and isofrequency lines correspond to lines where the color remains constant in the maps. Fig. S6 reports the results for the two sessions of subject 5.
The selected columnar region was used for the analysis of task-related changes in tuning width. That is, within each subject, we averaged the TW-values at each cortical depth for the two tasks separately (Fig. 4). Statistical testing was performed across subjects to evaluate the significance of the difference in TW values across tasks for each cortical depth (paired t test).
Furthermore, we evaluated the cortical depth-dependent anatomical contrast related to myelin (obtained from the T1w/T2*w images) in the columnar region compared with the remaining portion of HG sampled by the grid. Fig. S8 shows the profiles for the three subjects in which we acquired the anatomical data needed to compute the “myelin-related” contrast. In all subjects, the columnar region exhibited stronger contrast, indicative of higher myelin content, in the columnar region compared with the rest of HG. This difference was mostly observed in deeper cortical depths (i.e., closer to white matter).
Potential Effects of Imaging Acquisition on Estimation of Columns.
For all single-shot acquisitions, which include both conventional gradient-echo echo-planar imaging (GE-EPI) and 3D GRASE such as were used in the current study, signal decay during the readout induced image blurring. In GE-EPI, this blurring is manifested in the phase encode direction (in plane for every separately acquired slice). In 3D GRASE, this effect manifests most prominently in the slice direction because the sampling time is quite long. fMRI mapping techniques, based on the differential response between conditions (as in the case of tonotopic mapping), are less sensitive to detrimental blurring effects (see, e.g., ref. 18 for a simulation in the context of the blurring induced by the BOLD point spread function). Nevertheless, if significant blurring would manifest in a direction parallel to the columnar direction of our 3D grid, the results of our analysis would be biased by the image acquisition. To exclude this possibility, we estimated, for every grid point, the angle between the columnar direction at that point (defined by the direction of the grid across cortical depths) and the 3D GRASE slice acquisition direction. In this analysis, 0° angles indicate regions where the slice direction is aligned with the columnar direction: i.e., the worst case scenario for potential confounds due to acquisition-related blurring effects. Thus, if voxel blurring were responsible for the observed columnar responses, frequency columns would be present at all anatomical locations with small angles with respect to the slice acquisition direction independent of the underlying functional response. This effect was not present in any of our data (Fig. S7). In some subjects, the overlap was only partial (subjects 1 and 4) or only in regions with an angle greater than 10° (subject 3). The remaining subject showed minimal overlap with small-angle (0°–20°) regions. In summary, the analysis of the correspondence between the image acquisition direction (i.e., the slice direction) and the columnar direction shows that our identification of a columnar region of frequency responses in human PAC cannot be explained by the image acquisition-related blurring effects.
Simulation of Population Responses to the Sounds Across Tuning Width.
To illustrate that narrower tuning width increases the representational distance of upward and downward sweeps at the population level, we simulated neuronal population responses. Units were simulated to have a Gaussian frequency response with a best frequency (BF) distributed (uniformly) in the (0.2–6.4 kHz) range. The distribution of TW across the population changed between two different conditions in a manner similar to our data. Gaussian random noise was added to simulate noisy unit responses. The simulations were run at different levels of noise (5–25% of the unit maximal response) and using different numbers of units (10–100 per layer). The response of each unit to frequency sweeps (the sweeps were the same as used in our experiment) was computed.
To compute the distance between the population response to upward and downward sweeps, we first measured the correlation between each pair of population responses (i.e., the spatial correlation between the responses to two stimuli). These calculations were carried out per time bin of the sweep and then averaged over time. Second, we projected the computed distances in a 2D space using multidimensional scaling. To quantify the effect of sharpening, we measured the Euclidean distance between upward and downward sweeps in the resulting 2D space. The procedure is illustrated in Fig. 5, and the results show that the distance between upward and downward sweeps increases as the frequency tuning sharpens in supragranular layers.
SI Discussion
The availability of data collected in two separate scanning sessions in the same subject allowed us to evaluate the reproducibility of tonotopic maps and of the task-dependent changes. At a macroscopic level (i.e., when tonotopic maps were projected on the surface boundary of white and gray matter), tonotopic maps were remarkably stable (Fig. S1). This result indicates that T2-weighted functional MRI (i.e., 3D GRASE) has sufficient signal-to-noise to map the cortical representation of sound frequency in a reliable manner, even at the high spatial resolution used here. Furthermore, the reproducibility of our results indicates the reliability of the procedure we used (i.e., the use of a separate functional localizer to map the main tonotopic gradient) and the quality of the functional alignment across sessions. Moreover, in one of the subjects we evaluated the reproducibility of the columnarity by analyzing the data collected in two repeated sessions (Fig. S6). We found the same columnar region in the medial HG, the same representation of frequency in it, and similar task-related effects.
In animals, columnar responses to frequency have been measured in primary cortical areas. We focused our acquisition on the medial two-thirds of HG because there is consensus in the literature that this region includes the PAC (56, 57). Recently, it has been shown that the PAC can be localized by anatomical markers in vivo using acquisitions whose contrast is sensitive to the myelin content in the cortex (21, 60). The results of the analysis conducted in three of our subjects (Fig. S8) confirm that the columnar regions we identified have the anatomical signature of primary sensory cortices (i.e., high myelin content in deep to middle cortical layers).
Supplementary Material
Acknowledgments
This work was supported in part by Biomedical Technology Resource Centers, National Institute of Biomedical Imaging and Bioengineering Grant P41 EB015894. The 7-T magnet purchase was funded in part by the W. M. Keck Foundation, National Science Foundation Grant DBI-9907842, and National Institutes of Health Grant S10 RR1395. R.G. was supported by European Research Council Grant ERC-2010-AdG, 269853. E.F. was funded by The Netherlands Organisation for Scientific Research (NWO) VICI Grant 453-12-002. F.D.M. was funded by NWO VIDI Grant 864-13-012. M.M. was funded by NWO Rubicon Grant 446-12-010.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1507552112/-/DCSupplemental.
References
- 1.Merzenich MM, Reid MD. Representation of the cochlea within the inferior colliculus of the cat. Brain Res. 1974;77(3):397–415. doi: 10.1016/0006-8993(74)90630-1. [DOI] [PubMed] [Google Scholar]
- 2.De Martino F, et al. Spatial organization of frequency preference and selectivity in the human inferior colliculus. Nat Commun. 2013;4:1386. doi: 10.1038/ncomms2379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Merzenich MM, Brugge JF. Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res. 1973;50(2):275–296. doi: 10.1016/0006-8993(73)90731-2. [DOI] [PubMed] [Google Scholar]
- 4.Formisano E, et al. Mirror-symmetric tonotopic maps in human primary auditory cortex. Neuron. 2003;40(4):859–869. doi: 10.1016/s0896-6273(03)00669-x. [DOI] [PubMed] [Google Scholar]
- 5.Winer JA, Schreiner CE, editors. The Auditory Cortex. Springer; New York: 2009. [Google Scholar]
- 6.Linden JF, Schreiner CE. Columnar transformations in auditory cortex? A comparison to visual and somatosensory cortices. Cereb Cortex. 2003;13(1):83–89. doi: 10.1093/cercor/13.1.83. [DOI] [PubMed] [Google Scholar]
- 7.Abeles M, Goldstein MH., Jr Functional architecture in cat primary auditory cortex: Columnar organization and organization according to depth. J Neurophysiol. 1970;33(1):172–187. doi: 10.1152/jn.1970.33.1.172. [DOI] [PubMed] [Google Scholar]
- 8.Sugimoto S, Sakurada M, Horikawa J, Taniguchi I. The columnar and layer-specific response properties of neurons in the primary auditory cortex of Mongolian gerbils. Hear Res. 1997;112(1-2):175–185. doi: 10.1016/s0378-5955(97)00119-6. [DOI] [PubMed] [Google Scholar]
- 9.Shen JX, Xu ZM, Yao YD. Evidence for columnar organization in the auditory cortex of the mouse. Hear Res. 1999;137(1-2):174–177. doi: 10.1016/s0378-5955(99)00149-5. [DOI] [PubMed] [Google Scholar]
- 10.Shamma SA, Fleshman JW, Wiser PR, Versnel H. Organization of response areas in ferret primary auditory cortex. J Neurophysiol. 1993;69(2):367–383. doi: 10.1152/jn.1993.69.2.367. [DOI] [PubMed] [Google Scholar]
- 11.Imig TJ, Adrián HO. Binaural columns in the primary field (A1) of cat auditory cortex. Brain Res. 1977;138(2):241–257. doi: 10.1016/0006-8993(77)90743-0. [DOI] [PubMed] [Google Scholar]
- 12.Horton JC, Adams DL. The cortical column: A structure without a function. Philos Trans R Soc Lond B Biol Sci. 2005;360(1456):837–862. doi: 10.1098/rstb.2005.1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rakic P. Confusing cortical columns. Proc Natl Acad Sci USA. 2008;105(34):12099–12100. doi: 10.1073/pnas.0807271105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Petersen CC, Crochet S. Synaptic computation and sensory processing in neocortical layer 2/3. Neuron. 2013;78(1):28–48. doi: 10.1016/j.neuron.2013.03.020. [DOI] [PubMed] [Google Scholar]
- 15.Phillips DP, Irvine DR. Responses of single neurons in physiologically defined primary auditory cortex (AI) of the cat: Frequency tuning and responses to intensity. J Neurophysiol. 1981;45(1):48–58. doi: 10.1152/jn.1981.45.1.48. [DOI] [PubMed] [Google Scholar]
- 16.Atencio CA, Schreiner CE. Laminar diversity of dynamic sound processing in cat primary auditory cortex. J Neurophysiol. 2010;103(1):192–205. doi: 10.1152/jn.00624.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Atencio CA, Sharpee TO, Schreiner CE. Hierarchical computation in the canonical auditory cortical circuit. Proc Natl Acad Sci USA. 2009;106(51):21894–21899. doi: 10.1073/pnas.0908383106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yacoub E, Harel N, Ugurbil K. High-field fMRI unveils orientation columns in humans. Proc Natl Acad Sci USA. 2008;105(30):10607–10612. doi: 10.1073/pnas.0804110105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yacoub E, Shmuel A, Logothetis N, Uğurbil K. Robust detection of ocular dominance columns in humans using Hahn Spin Echo BOLD functional MRI at 7 Tesla. Neuroimage. 2007;37(4):1161–1177. doi: 10.1016/j.neuroimage.2007.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Van de Moortele P-F, et al. T1 weighted brain images at 7 Tesla unbiased for Proton Density, T2* contrast and RF coil receive B1 sensitivity with simultaneous vessel visualization. Neuroimage. 2009;46(2):432–446. doi: 10.1016/j.neuroimage.2009.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.De Martino F, et al. High-resolution mapping of myeloarchitecture in vivo: Localization of auditory areas in the human brain. Cereb Cortex. 2015;25(10):3394–3405. doi: 10.1093/cercor/bhu150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hackett TA, Preuss TM, Kaas JH. Architectonic identification of the core region in auditory cortex of macaques, chimpanzees, and humans. J Comp Neurol. 2001;441(3):197–222. doi: 10.1002/cne.1407. [DOI] [PubMed] [Google Scholar]
- 23.Meyer M, Liem F, Hirsiger S, Jäncke L, Hänggi J. Cortical surface area and cortical thickness demonstrate differential structural asymmetry in auditory-related areas of the human cortex. Cereb Cortex. 2014;24(10):2541–2552. doi: 10.1093/cercor/bht094. [DOI] [PubMed] [Google Scholar]
- 24.Ohl FW, Scheich H, Freeman WJ. Change in pattern of ongoing cortical activity with auditory category learning. Nature. 2001;412(6848):733–736. doi: 10.1038/35089076. [DOI] [PubMed] [Google Scholar]
- 25.Polimeni JR, Fischl B, Greve DN, Wald LL. Laminar analysis of 7T BOLD using an imposed spatial activation pattern in human V1. Neuroimage. 2010;52(4):1334–1346. doi: 10.1016/j.neuroimage.2010.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ress D, Glover GH, Liu J, Wandell B. Laminar profiles of functional activity in the human brain. Neuroimage. 2007;34(1):74–84. doi: 10.1016/j.neuroimage.2006.08.020. [DOI] [PubMed] [Google Scholar]
- 27.Koopmans PJ, Barth M, Norris DG. Layer-specific BOLD activation in human V1. Hum Brain Mapp. 2010;31(9):1297–1304. doi: 10.1002/hbm.20936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Koopmans PJ, Barth M, Orzada S, Norris DG. Multi-echo fMRI of the cortical laminae in humans at 7 T. Neuroimage. 2011;56(3):1276–1285. doi: 10.1016/j.neuroimage.2011.02.042. [DOI] [PubMed] [Google Scholar]
- 29.Siero JCW, Petridou N, Hoogduin H, Luijten PR, Ramsey NF. Cortical depth-dependent temporal dynamics of the BOLD response in the human brain. J Cereb Blood Flow Metab. 2011;31(10):1999–2008. doi: 10.1038/jcbfm.2011.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.De Martino F, et al. Cortical depth dependent functional responses in humans at 7T: Improved specificity with 3D GRASE. PLoS One. 2013;8(3):e60514. doi: 10.1371/journal.pone.0060514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Petkov CI, et al. Attentional modulation of human auditory cortex. Nat Neurosci. 2004;7(6):658–663. doi: 10.1038/nn1256. [DOI] [PubMed] [Google Scholar]
- 32.Da Costa S, van der Zwaag W, Miller LM, Clarke S, Saenz M. Tuning in to sound: Frequency-selective attentional filter in human primary auditory cortex. J Neurosci. 2013;33(5):1858–1863. doi: 10.1523/JNEUROSCI.4405-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Oh J, Kwon JH, Yang PS, Jeong J. Auditory imagery modulates frequency-specific areas in the human auditory cortex. J Cogn Neurosci. 2013;25(2):175–187. doi: 10.1162/jocn_a_00280. [DOI] [PubMed] [Google Scholar]
- 34.Paltoglou AE, Sumner CJ, Hall DA. Examining the role of frequency specificity in the enhancement and suppression of human cortical activity by auditory selective attention. Hear Res. 2009;257(1-2):106–118. doi: 10.1016/j.heares.2009.08.007. [DOI] [PubMed] [Google Scholar]
- 35.Lakatos P, et al. The leading sense: Supramodal control of neurophysiological context by attention. Neuron. 2009;64(3):419–430. doi: 10.1016/j.neuron.2009.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.O’Connell MN, Barczak A, Schroeder CE, Lakatos P. Layer specific sharpening of frequency tuning by selective attention in primary auditory cortex. J Neurosci. 2014;34(49):16496–16508. doi: 10.1523/JNEUROSCI.2055-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fritz J, Shamma S, Elhilali M, Klein D. Rapid task-related plasticity of spectrotemporal receptive fields in primary auditory cortex. Nat Neurosci. 2003;6(11):1216–1223. doi: 10.1038/nn1141. [DOI] [PubMed] [Google Scholar]
- 38.Fritz JB, Elhilali M, Shamma SA. Differential dynamic plasticity of A1 receptive fields during multiple spectral tasks. J Neurosci. 2005;25(33):7623–7635. doi: 10.1523/JNEUROSCI.1318-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Santoro R, et al. Encoding of natural sounds at multiple spectral and temporal resolutions in the human auditory cortex. PLOS Comput Biol. 2014;10(1):e1003412. doi: 10.1371/journal.pcbi.1003412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Constantinople CM, Bruno RM. Deep cortical layers are activated directly by thalamus. Science. 2013;340(6140):1591–1594. doi: 10.1126/science.1236425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Oshio K, Feinberg DA. GRASE (Gradient- and spin-echo) imaging: A novel fast MRI technique. Magn Reson Med. 1991;20(2):344–349. doi: 10.1002/mrm.1910200219. [DOI] [PubMed] [Google Scholar]
- 42.Vaughan JT, et al. 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Magn Reson Med. 2001;46(1):24–30. doi: 10.1002/mrm.1156. [DOI] [PubMed] [Google Scholar]
- 43.Uğurbil K, et al. Ultrahigh field magnetic resonance imaging and spectroscopy. Magn Reson Imaging. 2003;21(10):1263–1281. doi: 10.1016/j.mri.2003.08.027. [DOI] [PubMed] [Google Scholar]
- 44.Ogawa S, et al. Intrinsic signal changes accompanying sensory stimulation: Functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci USA. 1992;89(13):5951–5955. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yacoub E, et al. Imaging brain function in humans at 7 Tesla. Magn Reson Med. 2001;45(4):588–594. doi: 10.1002/mrm.1080. [DOI] [PubMed] [Google Scholar]
- 46.Zhao F, Wang P, Hendrich K, Ugurbil K, Kim S-G. Cortical layer-dependent BOLD and CBV responses measured by spin-echo and gradient-echo fMRI: Insights into hemodynamic regulation. Neuroimage. 2006;30(4):1149–1160. doi: 10.1016/j.neuroimage.2005.11.013. [DOI] [PubMed] [Google Scholar]
- 47.Harel N, Lin J, Moeller S, Ugurbil K, Yacoub E. Combined imaging-histological study of cortical laminar specificity of fMRI signals. Neuroimage. 2006;29(3):879–887. doi: 10.1016/j.neuroimage.2005.08.016. [DOI] [PubMed] [Google Scholar]
- 48.Uludağ K, Müller-Bierl B, Uğurbil K. An integrative model for neuronal activity-induced signal changes for gradient and spin echo functional imaging. Neuroimage. 2009;48(1):150–165. doi: 10.1016/j.neuroimage.2009.05.051. [DOI] [PubMed] [Google Scholar]
- 49.Yacoub E, Van De Moortele P-F, Shmuel A, Uğurbil K. Signal and noise characteristics of Hahn SE and GE BOLD fMRI at 7 T in humans. Neuroimage. 2005;24(3):738–750. doi: 10.1016/j.neuroimage.2004.09.002. [DOI] [PubMed] [Google Scholar]
- 50.Goense JBM, Zappe A-C, Logothetis NK. High-resolution fMRI of macaque V1. Magn Reson Imaging. 2007;25(6):740–747. doi: 10.1016/j.mri.2007.02.013. [DOI] [PubMed] [Google Scholar]
- 51.Goense JBM, Logothetis NK. Laminar specificity in monkey V1 using high-resolution SE-fMRI. Magn Reson Imaging. 2006;24(4):381–392. doi: 10.1016/j.mri.2005.12.032. [DOI] [PubMed] [Google Scholar]
- 52.Norris DG. Spin-echo fMRI: The poor relation? Neuroimage. 2012;62(2):1109–1115. doi: 10.1016/j.neuroimage.2012.01.003. [DOI] [PubMed] [Google Scholar]
- 53.Feinberg DA, Harel N, Ramanna S, Ugurbil K, Yacoub E. Sub-millimeter single-shot 3D GRASE with inner volume selection for T2-weighted fMRI applications at 7T. Proc Int Soc Mag Reson Med. 2008;16:2373. [Google Scholar]
- 54.Zimmermann J, et al. Mapping the organization of axis of motion selective features in human area MT using high-field fMRI. PLoS One. 2011;6(12):e28716. doi: 10.1371/journal.pone.0028716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Olman C, et al. Layer-specific fMRI reflect different nuronal computations at different depths in human V1. PLoS ONE. 2012;7(3):e32536. doi: 10.1371/journal.pone.0032536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Baumann S, Petkov CI, Griffiths TD. A unified framework for the organization of the primate auditory cortex. Front Syst Neurosci. 2013;7:11. doi: 10.3389/fnsys.2013.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Moerel M, De Martino F, Formisano E. An anatomical and functional topography of human auditory cortical areas. Front Neurosci. 2014;8:225. doi: 10.3389/fnins.2014.00225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sled JG, Zijdenbos AP, Evans AC. 1997. A comparison of retrospective intensity non-uniformity correction methods for MRI. Information Processing in Medical, Imaging Lecture Notes in Computer Science (Springer, Berlin), Vol 1230, pp 459–464.
- 59.Jones SE, Buchbinder BR, Aharon I. Three-dimensional mapping of cortical thickness using Laplace’s equation. Hum Brain Mapp. 2000;11(1):12–32. doi: 10.1002/1097-0193(200009)11:1<12::AID-HBM20>3.0.CO;2-K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Glasser MF, Goyal MS, Preuss TM, Raichle ME, Van Essen DC. Trends and properties of human cerebral cortex: Correlations with cortical myelin content. Neuroimage. 2014;93(Pt 2):165–175. doi: 10.1016/j.neuroimage.2013.03.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.