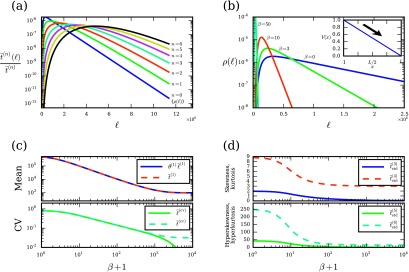
FIG. 2.

Distributions of path lengths and times on a 1D lattice. (a) The nth time moments ${\overline{t}}^{\left(n\right)}\left(\ell \right)$ for paths of length ℓ, normalized as fractions of the total moments ${\overline{t}}^{\left(n\right)}$, in the absence of a potential energy. (b) Path length probability distribution ρ(ℓ) for several choices of β on a linear energy landscape V(x) (inset). (c) The mean path length ${\overline{\ell }}^{\left(1\right)}$ (scaled by the mean waiting time θ⁽¹⁾ = 1/2 for bulk states), mean path time ${\overline{t}}^{\left(1\right)}$, path length CV ${\overline{\ell }}^{\left(\mathrm{cv}\right)}$, and path time CV ${\overline{t}}^{\left(\mathrm{cv}\right)}$ as functions of β. (d) Skewness ${\overline{t}}_{\mathrm{std}}^{\left(3\right)}$, kurtosis ${\overline{t}}_{\mathrm{std}}^{\left(4\right)}$, hyperskewness ${\overline{t}}_{\mathrm{std}}^{\left(5\right)}$, and hyperkurtosis ${\overline{t}}_{\mathrm{std}}^{\left(6\right)}$ of path time as functions of β. Values of β in (c) and (d) are shifted by 1 to show β = 0 on a log scale. In all panels, we use a lattice of length L = 1000 with transition rates given by Eq. (63).