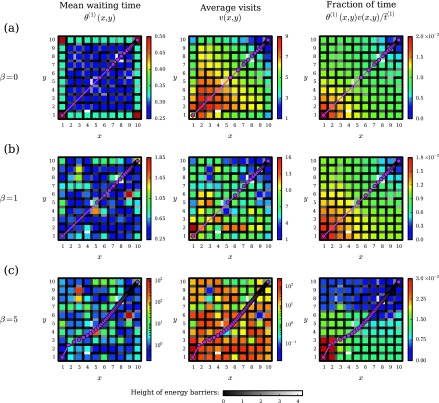
FIG. 5.

Spatial properties of first-passage paths in the random barrier model. For a 10 × 10 lattice, we show statistics of first-passage paths from (1, 1) to (10, 10) for a single quenched realization of the energy barriers. Each colored cell corresponds to a lattice point (x, y), with gray-scale bars indicating energy barriers between lattice points (higher energies are white, lower energies are black). Energy barriers are randomly sampled from an exponential distribution with mean E₀ = 1, and the transition rate across a zero energy barrier is Γ₀ = 1. The leftmost column shows the mean waiting time θ⁽¹⁾(x, y), the middle column is the average number of visits v(x, y), and the rightmost column is the average fraction of time ${\theta }^{\left(1\right)}(x,y)v(x,y)/{\overline{t}}^{\left(1\right)}$ spent at each lattice point. Rows correspond to different inverse temperatures: (a) β = 0, (b) β = 1, and (c) β = 5. Magenta points show the average particle position for every 100th jump (connected by straight lines to guide the eye).